余角与补角
图片预览





文档简介
课件23张PPT。4.3.3 余角和补角12比萨斜塔 2互为余角(互余):
如果两个角的和是90°(直角),那么这两个角叫做互为余角,其中一个角是另一个角的余角。
即:∠1是∠2的余角或∠2是∠1的余角.
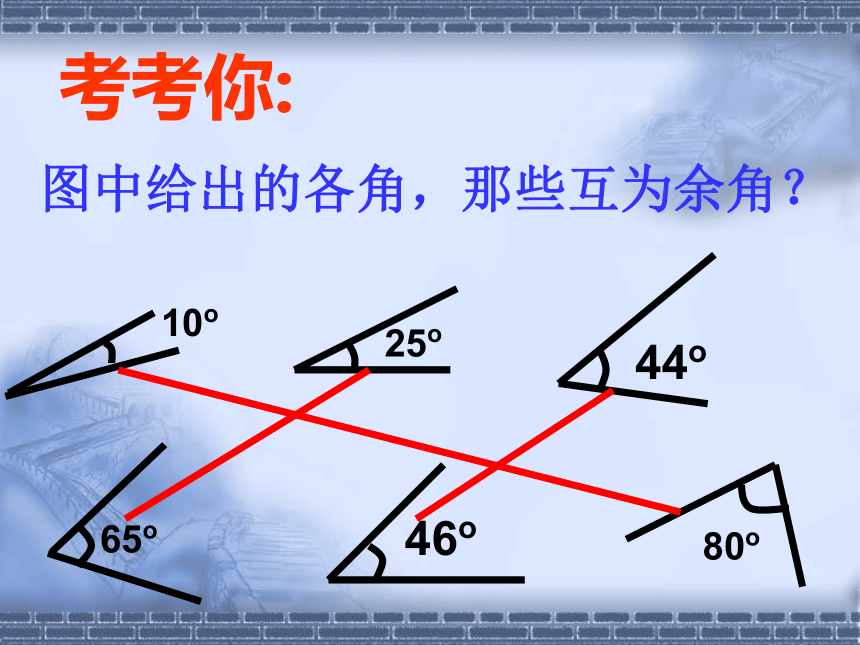
图中给出的各角,那些互为余角?10o25o65o80o44o46o考考你:34比萨斜塔 4互为补角(互补):
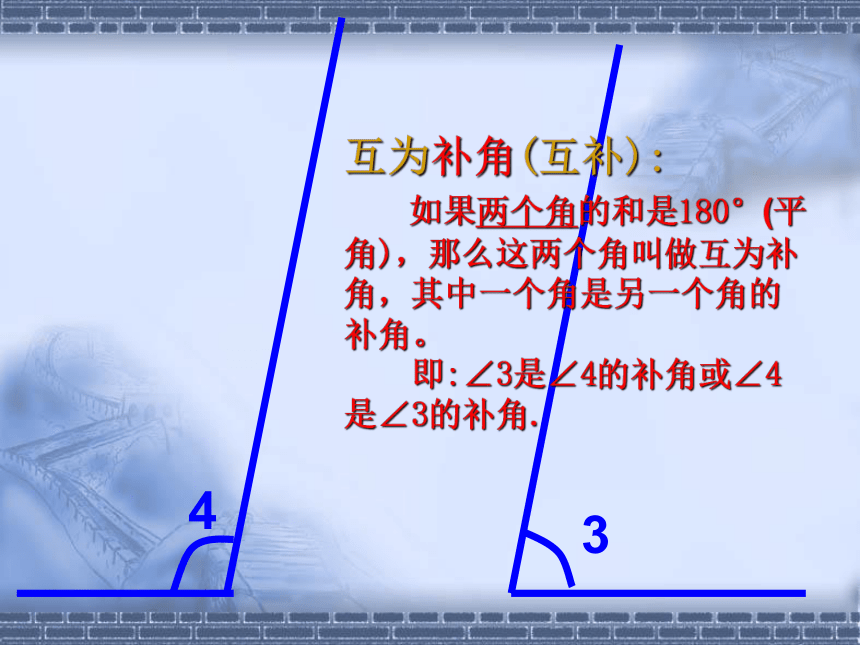
如果两个角的和是180°(平角),那么这两个角叫做互为补角,其中一个角是另一个角的补角。
即:∠3是∠4的补角或∠4是∠3的补角.
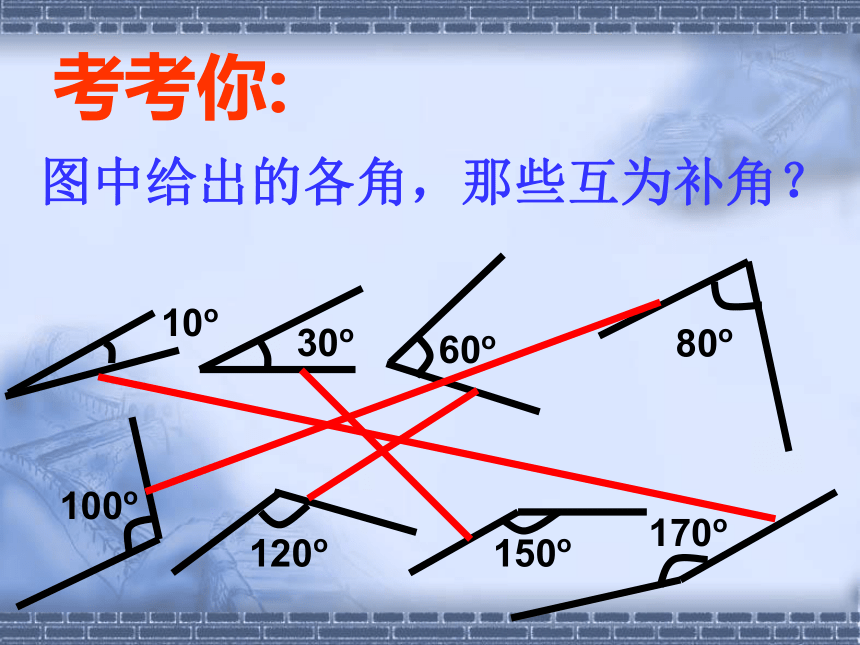
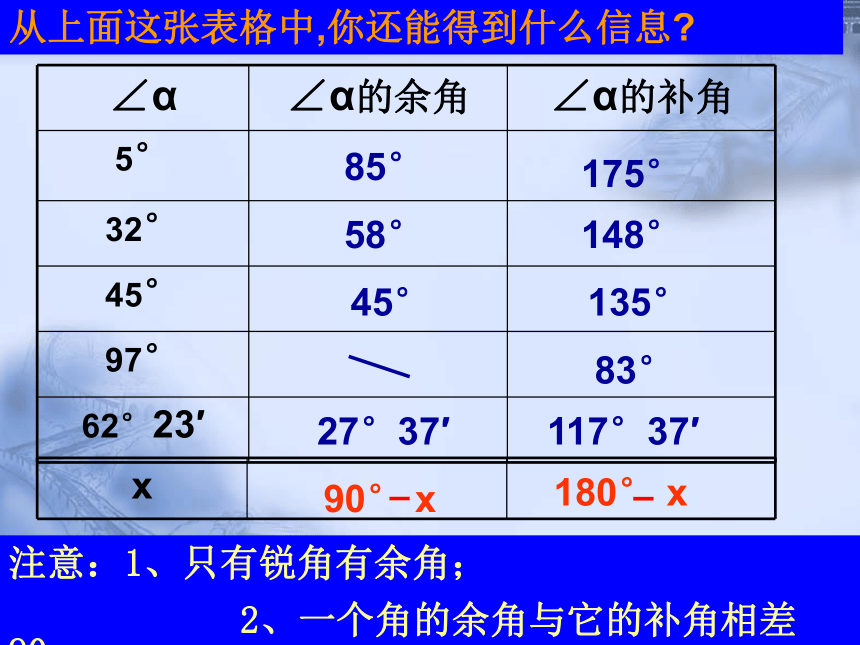
图中给出的各角,那些互为补角?10o30o60o80o100o120o150o170o考考你:填表27°37′117°37′85°175°58°148°45°135°83°从上面这张表格中,你还能得到什么信息?注意:1、只有锐角有余角;
2、一个角的余角与它的补角相差90°.例1: 若一个角的补角等于它的余角的4倍,求这个角的度数。解:设这个角是x °,则它的补角是(180-x°),余角是(90°-x°) ,根据题意得:(180-x)= 4 (90-x)解得: x = 60答:这个角的度数是60 °。练习
一个角的补角是它的3倍,这个角是多少度?解:设这个角为x°,则它的补角为(180°-x°),得:180 – x = 3 x解之得: x = 45答:这个角是45°。 如图∠1 与∠2互补,∠1 与∠3互补 ,那么∠2与∠3相等吗?为什么?补角的性质∵ ∠1 与∠2互补,
∴ ∠2= 180 °-___;∠1答:∠2与∠3相等。同角的补角相等∵ ∠1与∠3互补 ,
∴___________。∠3 = 180° -∠1∴________。∠2=∠3探究1理由如下: 如图∠1 与∠2互补,∠3 与∠4互补 ,如果∠1=∠3,那么∠2与∠4相等吗?为什么?补角性质:
等角的补角相等探究1补角的性质补角的性质解:∵ ∠1 +∠2=180°, ∠3 +∠4=180°∴ ∠2=180°-∠1 , ∠4=180°- ∠3∵ ∠1 =∠3∴ 180°-∠1 =180°- ∠3即:∠2 =∠4 如图∠1 与∠2互补,∠3 与∠4互补 ,如果∠1=∠3,那么∠2与∠4相等吗?为什么?
同角或等角的补角相等补角性质:分析: ∠AOB = 90 °则______+ ∠BOD = 90 °;同角的余角相等余角的性质∠COD = 90 °则 _____+ ∠BOD = 90 °答:∠1 = ∠2∠1∠2 如图∠1 与∠2互余,∠3 与∠4互余 ,如果∠1=∠3,那么∠2与∠4相等吗?为什么?探究:余角的性质余角性质:
等角的余角相等探究:余角的性质 如图∠1 与∠2互余,∠3 与∠4互余 ,如果∠1=∠3,那么∠2与∠4相等吗?为什么?解:∵ ∠1 +∠2=90°, ∠3 +∠4=90°∴ ∠2=90°-∠1 , ∠4=90°- ∠3∵ ∠1 =∠3∴ 90°-∠1 =90°- ∠3即:∠2 =∠4同角或等角的余角相等余角性质:∠1=120 °, ∠1与∠2互补, ∠3与∠2互余,则∠3= .
2.O为直线AB上的一点,OD平分∠AOB, ∠COE = 90 °
则∠BOC = ,
∠COD = 。检测∠DOE∠AOE30 °3.如图,E、F是直线DG上两点,
∠1 = ∠2,∠3 = ∠4 = 90 °找出图中相等的角并说明理由。答:∠AEF = ∠CFE,∠5 = ∠6。如图,已知AOB是一直线,OC是∠ AOB的平分线, ∠ DOE是直角,图中哪些角相等?哪些角互余?哪些角互补?(至少三对)B讨论答:相等的角有: ∠AOC= ∠BOC= ∠DOE = 90° ;
∠ 1= ∠ 4; ∠ 2= ∠ 3;互余的角有: ∠ 1 + ∠ 2= 90° ;
∠ 3 + ∠ 4= 90° ;
∠ 1 + ∠ 3= 90° ;
∠ 2 + ∠ 4= 90° ; 互补的角有: ∠AOC +∠BOC = 180°;
∠ 4+ ∠ EOB= 180°;
∠ 1+ ∠ EOB= 180°;
∠ 2+ ∠ AOD= 180°;
∠ 3+ ∠ AOD= 180°;
等等 本节课你学到了哪些知识?请你说一说.互余和互补∠1+∠2=90°∠1+∠2=180°同角或等角的余角相等同角或等角的补角相等作业:
1、作业本(1)
2、试卷
3.教与学(部分)
如果两个角的和是90°(直角),那么这两个角叫做互为余角,其中一个角是另一个角的余角。
即:∠1是∠2的余角或∠2是∠1的余角.
图中给出的各角,那些互为余角?10o25o65o80o44o46o考考你:34比萨斜塔 4互为补角(互补):
如果两个角的和是180°(平角),那么这两个角叫做互为补角,其中一个角是另一个角的补角。
即:∠3是∠4的补角或∠4是∠3的补角.
图中给出的各角,那些互为补角?10o30o60o80o100o120o150o170o考考你:填表27°37′117°37′85°175°58°148°45°135°83°从上面这张表格中,你还能得到什么信息?注意:1、只有锐角有余角;
2、一个角的余角与它的补角相差90°.例1: 若一个角的补角等于它的余角的4倍,求这个角的度数。解:设这个角是x °,则它的补角是(180-x°),余角是(90°-x°) ,根据题意得:(180-x)= 4 (90-x)解得: x = 60答:这个角的度数是60 °。练习
一个角的补角是它的3倍,这个角是多少度?解:设这个角为x°,则它的补角为(180°-x°),得:180 – x = 3 x解之得: x = 45答:这个角是45°。 如图∠1 与∠2互补,∠1 与∠3互补 ,那么∠2与∠3相等吗?为什么?补角的性质∵ ∠1 与∠2互补,
∴ ∠2= 180 °-___;∠1答:∠2与∠3相等。同角的补角相等∵ ∠1与∠3互补 ,
∴___________。∠3 = 180° -∠1∴________。∠2=∠3探究1理由如下: 如图∠1 与∠2互补,∠3 与∠4互补 ,如果∠1=∠3,那么∠2与∠4相等吗?为什么?补角性质:
等角的补角相等探究1补角的性质补角的性质解:∵ ∠1 +∠2=180°, ∠3 +∠4=180°∴ ∠2=180°-∠1 , ∠4=180°- ∠3∵ ∠1 =∠3∴ 180°-∠1 =180°- ∠3即:∠2 =∠4 如图∠1 与∠2互补,∠3 与∠4互补 ,如果∠1=∠3,那么∠2与∠4相等吗?为什么?
同角或等角的补角相等补角性质:分析: ∠AOB = 90 °则______+ ∠BOD = 90 °;同角的余角相等余角的性质∠COD = 90 °则 _____+ ∠BOD = 90 °答:∠1 = ∠2∠1∠2 如图∠1 与∠2互余,∠3 与∠4互余 ,如果∠1=∠3,那么∠2与∠4相等吗?为什么?探究:余角的性质余角性质:
等角的余角相等探究:余角的性质 如图∠1 与∠2互余,∠3 与∠4互余 ,如果∠1=∠3,那么∠2与∠4相等吗?为什么?解:∵ ∠1 +∠2=90°, ∠3 +∠4=90°∴ ∠2=90°-∠1 , ∠4=90°- ∠3∵ ∠1 =∠3∴ 90°-∠1 =90°- ∠3即:∠2 =∠4同角或等角的余角相等余角性质:∠1=120 °, ∠1与∠2互补, ∠3与∠2互余,则∠3= .
2.O为直线AB上的一点,OD平分∠AOB, ∠COE = 90 °
则∠BOC = ,
∠COD = 。检测∠DOE∠AOE30 °3.如图,E、F是直线DG上两点,
∠1 = ∠2,∠3 = ∠4 = 90 °找出图中相等的角并说明理由。答:∠AEF = ∠CFE,∠5 = ∠6。如图,已知AOB是一直线,OC是∠ AOB的平分线, ∠ DOE是直角,图中哪些角相等?哪些角互余?哪些角互补?(至少三对)B讨论答:相等的角有: ∠AOC= ∠BOC= ∠DOE = 90° ;
∠ 1= ∠ 4; ∠ 2= ∠ 3;互余的角有: ∠ 1 + ∠ 2= 90° ;
∠ 3 + ∠ 4= 90° ;
∠ 1 + ∠ 3= 90° ;
∠ 2 + ∠ 4= 90° ; 互补的角有: ∠AOC +∠BOC = 180°;
∠ 4+ ∠ EOB= 180°;
∠ 1+ ∠ EOB= 180°;
∠ 2+ ∠ AOD= 180°;
∠ 3+ ∠ AOD= 180°;
等等 本节课你学到了哪些知识?请你说一说.互余和互补∠1+∠2=90°∠1+∠2=180°同角或等角的余角相等同角或等角的补角相等作业:
1、作业本(1)
2、试卷
3.教与学(部分)
