圆周角和圆心角

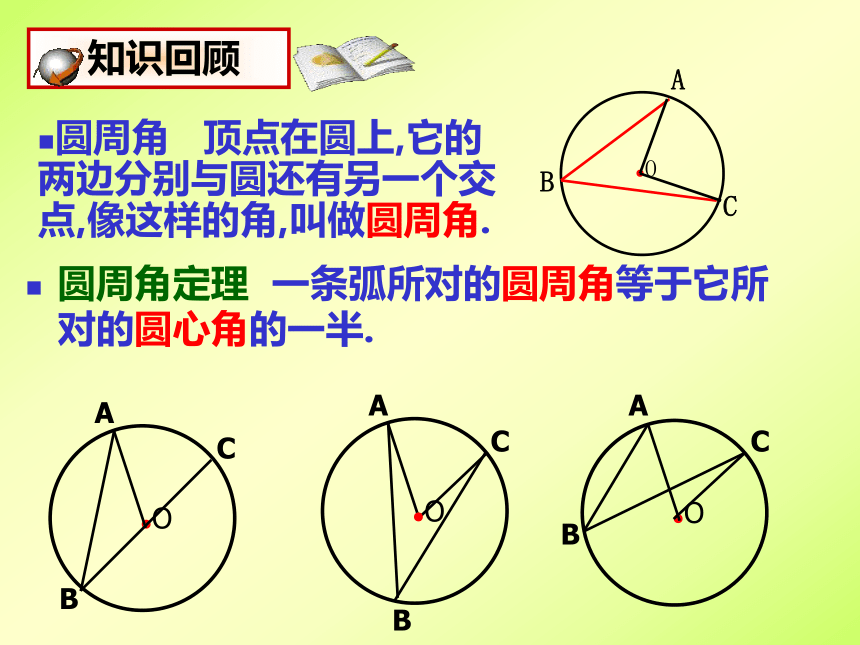
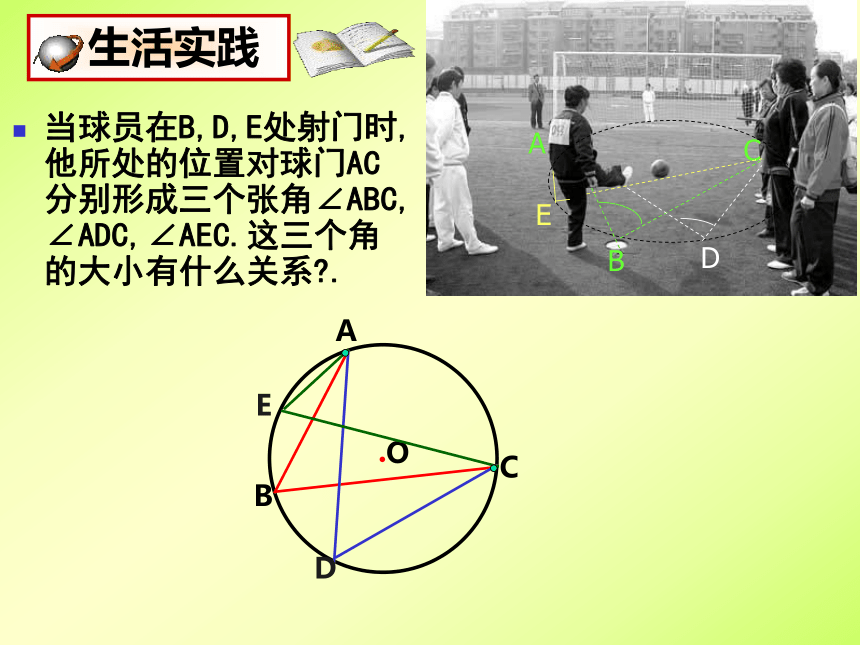
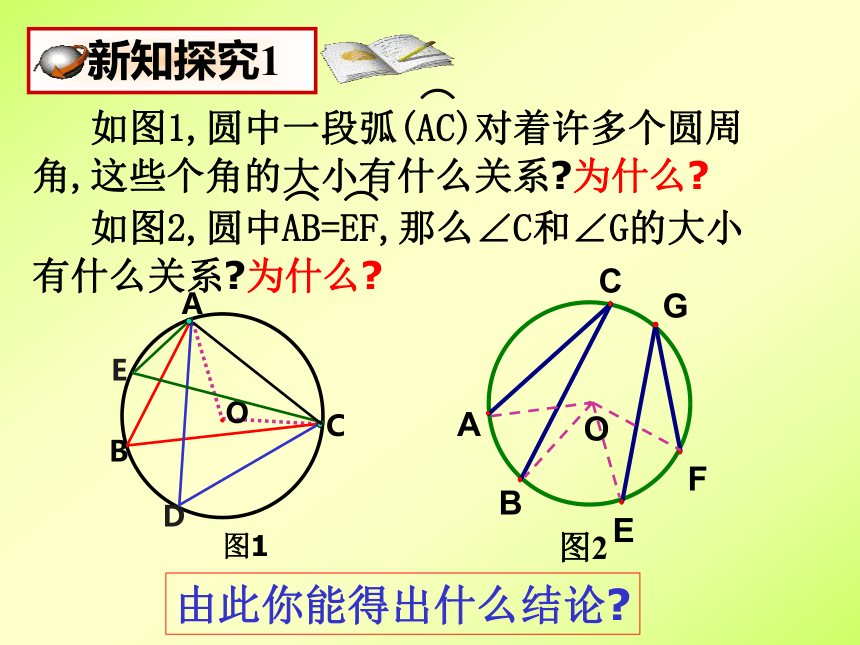
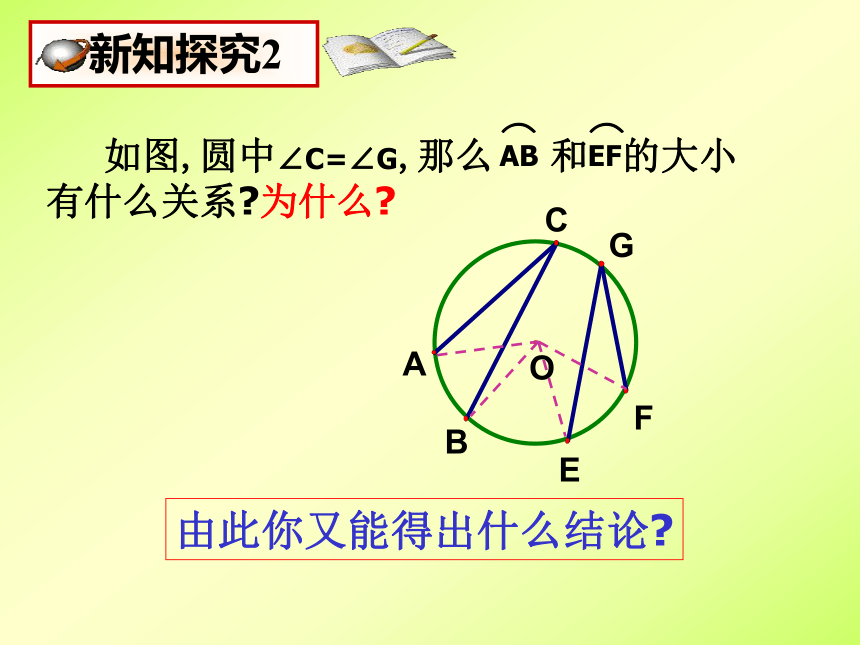
课件18张PPT。九年级数学(下)第三章 圆圆周角和圆心角的关系(2)市二中 徐红丽圆周角 顶点在圆上,它的两边分别与圆还有另一个交点,像这样的角,叫做圆周角.圆周角定理 一条弧所对的圆周角等于它所对的圆心角的一半.当球员在B,D,E处射门时,他所处的位置对球门AC分别形成三个张角∠ABC, ∠ADC,∠AEC.这三个角的大小有什么关系?.C由此你能得出什么结论?由此你又能得出什么结论?用于找相等的弧圆周角定理的推论1：同圆或等圆中，同弧或等弧所对的圆周角相等；
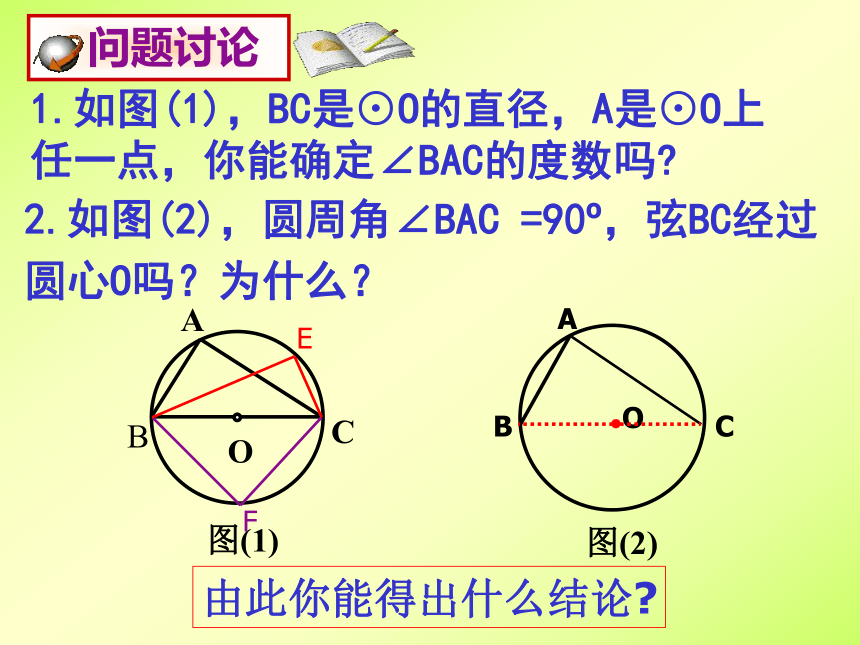
相等的圆周角所对的弧也相等.用于找相等的角1.如图(1)，BC是⊙O的直径，A是⊙O上任一点，你能确定∠BAC的度数吗?2.如图(2)，圆周角∠BAC =90o，弦BC经过圆心O吗？为什么？由此你能得出什么结论?用于判断某条弦是否是直径用于构造角圆周角定理的推论2：半圆（或直径）所对的圆周角是直角；
90°的圆周角所对的弦是直径。圆周角定理的推论：推论1 同圆或等圆中，同弧或等弧所对的圆周角相等；相等的圆周角所对的弧也相等.推论2 半圆（或直径）所对的圆周角是直角； 90°的圆周角所对的弦是直径. 1.如图,AB是⊙O的直径，BD是弦,延长BD到C,使DC=BD,AC与AB的大小有什么关系?为什么?课堂练习1.判断题：
（1）等弧所对的圆周角相等. （ ）
（2）相等的圆周角所对的弧也相等.（ ）
（3）90°的角所对的弦是直径. （ ）
（4）同弦所对的圆周角相等. （ ）
√XXX2.填空题:
(1)如图所示,
∠BAC= ,∠DAC= .∠DBC∠BDC(2)如图所示,⊙O的直径AB=10cm,
C为⊙O上一点,∠BAC=30°,
则BC= cm 53.如图,△ABC的顶点均在⊙O上,
AB=4, ∠C=30°,求⊙O的直径. E 如图，以⊙O的半径OA为直径作⊙O1,
⊙O的弦AD交⊙O1于C,则
(1)OC与AD的位置关系是_____ ;
(2)OC与BD的位置关系是_____ ;
(3)若OC = 2cm,则BD = __ cm。OC垂直平分AD平 行4知识深化C1、本节课我们学习了哪些知识？
小结圆周角定理的两个推论引辅助线的方法：
（1）构造直径上的圆周角。
（2）构造同弧所对的圆周角。2、本节课我们学习了哪些方法？ 如图，AE⊙O的直径, △ABC的顶点都在⊙O上,AD是△ABC的高; 求证：AB · AC = AE · ADAOBCDE分析：要证AB · AC = AE · AD△ADC∽ △ABE或△ACE∽ △ADB综合运用1.课本P116习题3.5 1,2题