22.3 实际问题与二次函数应用题 期末综合检测(含答案) 2023-2024学年人教版数学九年级上册
文档属性
| 名称 | 22.3 实际问题与二次函数应用题 期末综合检测(含答案) 2023-2024学年人教版数学九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 225.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-17 00:00:00 | ||
图片预览

文档简介
22.3 实际问题与二次函数应用题
1.某工厂生产的某种产品按质量分为10个档次,第1档次(最低档次)的产品一天能生产95件,每件利润6元.每提高一个档次,每件利润增加2元,但一天产量减少5件.
(1)若生产第x档次的产品一天的总利润为y元(其中x为正整数,且1≤x≤10),求出y关于x的函数关系式;
(2)若生产第x档次的产品一天的总利润为1120元,求该产品的质量档次.
2.为了节省材料,某水产养殖户利用水库的岸堤(岸堤足够长)为一边,用总长为40m的围网
在水库中围成了如图所示的①②二块矩形区域.设BC的长度为xm,矩形区域ABCD的面积为
ym2.
(1)求y与x之间的函数关系式;
(2)为何值时,y有最大值?最大值是多少?
3.某童装店购进一批20元/件的童装,由销售经验知,每天的销售量y(件)与销售单价x(元)之间存在如图的一次函数关系.
(1)求y与x之间的函数关系.
(2)当销售单价定为多少时,每天可获得最大利益,最大利润是多少?
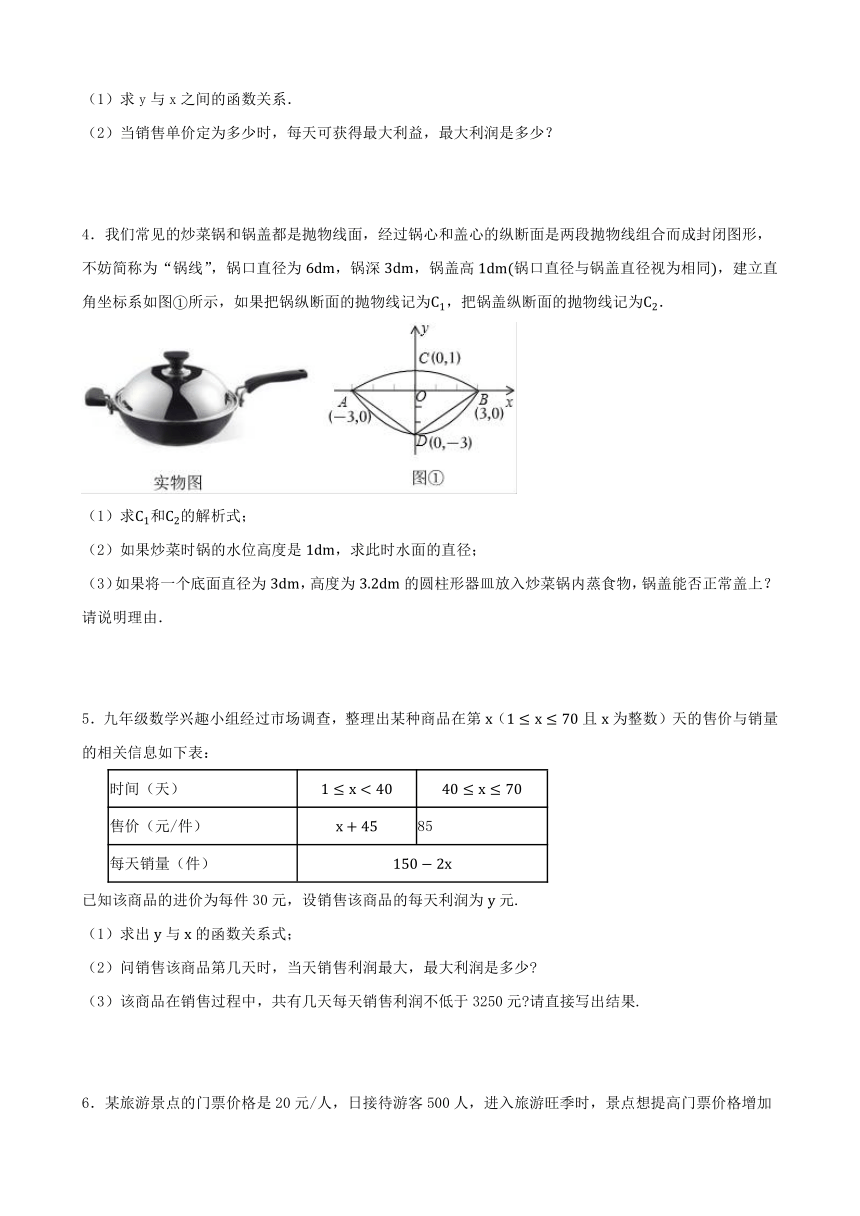
4.我们常见的炒菜锅和锅盖都是抛物线面,经过锅心和盖心的纵断面是两段抛物线组合而成封闭图形,不妨简称为“锅线”,锅口直径为,锅深,锅盖高锅口直径与锅盖直径视为相同,建立直角坐标系如图所示,如果把锅纵断面的抛物线记为,把锅盖纵断面的抛物线记为.
(1)求和的解析式;
(2)如果炒菜时锅的水位高度是,求此时水面的直径;
(3)如果将一个底面直径为,高度为的圆柱形器皿放入炒菜锅内蒸食物,锅盖能否正常盖上?请说明理由.
5.九年级数学兴趣小组经过市场调查,整理出某种商品在第(且为整数)天的售价与销量的相关信息如下表:
时间(天)
售价(元/件) 85
每天销量(件)
已知该商品的进价为每件30元,设销售该商品的每天利润为元.
(1)求出与的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少
(3)该商品在销售过程中,共有几天每天销售利润不低于3250元 请直接写出结果.
6.某旅游景点的门票价格是20元/人,日接待游客500人,进入旅游旺季时,景点想提高门票价格增加盈利.经过市场调查发现,门票价格每提高5元,日接待游客人数就会减少50人.设提价后的门票价格为x(元/人)(x>20),日接待游客的人数为y(人).
(1)求y与x(x>20)的函数关系式;
(2)已知景点每日的接待成本为z(元),z与y满足函数关系式:z=100+10y.求z与x的函数关系式;
(3)在(2)的条件下,当门票价格为多少时,景点每日获取的利润最大?最大利润是多少?(利润=门票收入﹣接待成本)
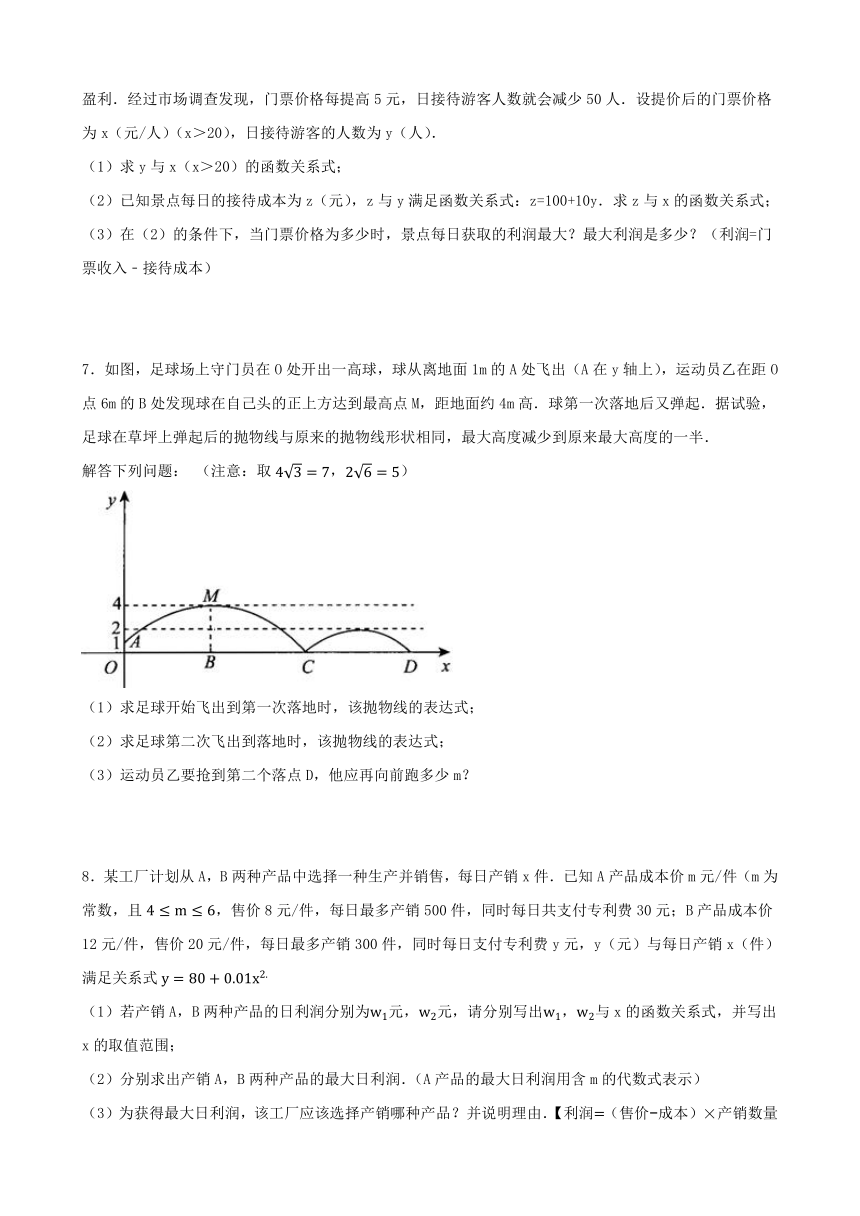
7.如图,足球场上守门员在O处开出一高球,球从离地面1m的A处飞出(A在y轴上),运动员乙在距O点6m的B处发现球在自己头的正上方达到最高点M,距地面约4m高.球第一次落地后又弹起.据试验,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.
解答下列问题: (注意:取,)
(1)求足球开始飞出到第一次落地时,该抛物线的表达式;
(2)求足球第二次飞出到落地时,该抛物线的表达式;
(3)运动员乙要抢到第二个落点D,他应再向前跑多少m?
8.某工厂计划从A,B两种产品中选择一种生产并销售,每日产销x件.已知A产品成本价m元/件(m为常数,且,售价8元/件,每日最多产销500件,同时每日共支付专利费30元;B产品成本价12元/件,售价20元/件,每日最多产销300件,同时每日支付专利费y元,y(元)与每日产销x(件)满足关系式
(1)若产销A,B两种产品的日利润分别为元,元,请分别写出,与x的函数关系式,并写出x的取值范围;
(2)分别求出产销A,B两种产品的最大日利润.(A产品的最大日利润用含m的代数式表示)
(3)为获得最大日利润,该工厂应该选择产销哪种产品?并说明理由.【利润(售价成本)产销数量专利费】
9.某F2C直营店招牌:“新进最新款洗发水40瓶,每件售价80元,若一次性购买不超过10瓶时,售价不变;若一次性购买超过10瓶时,每多买1瓶,所买的每瓶洗发水的售价均降低2元.”已知该瓶洗发水每瓶进价52元,设顾客一次性购买洗发水x瓶时,他所付洗发水单价y元,该直营店所获利润为W元.
(1)求y与x的函数关系式,并写出自变量x的取值范围;
(2)顾客一次性购买多少瓶时,该直营店从中获利最多?
10.小王电子产品专柜以20元/副的价格批发了某新款耳机,在试销的60天内整理出了销售数据如下
销售数据(第x天) 售价(元) 日销售量(副)
1≤x<35 x+30 100﹣2x
35≤x≤60 70 100﹣2x
(1)若试销阶段每天的利润为W元,求出W与x的函数关系式;
(2)请问在试销阶段的哪一天销售利润W可以达到最大值?最大值为多少?
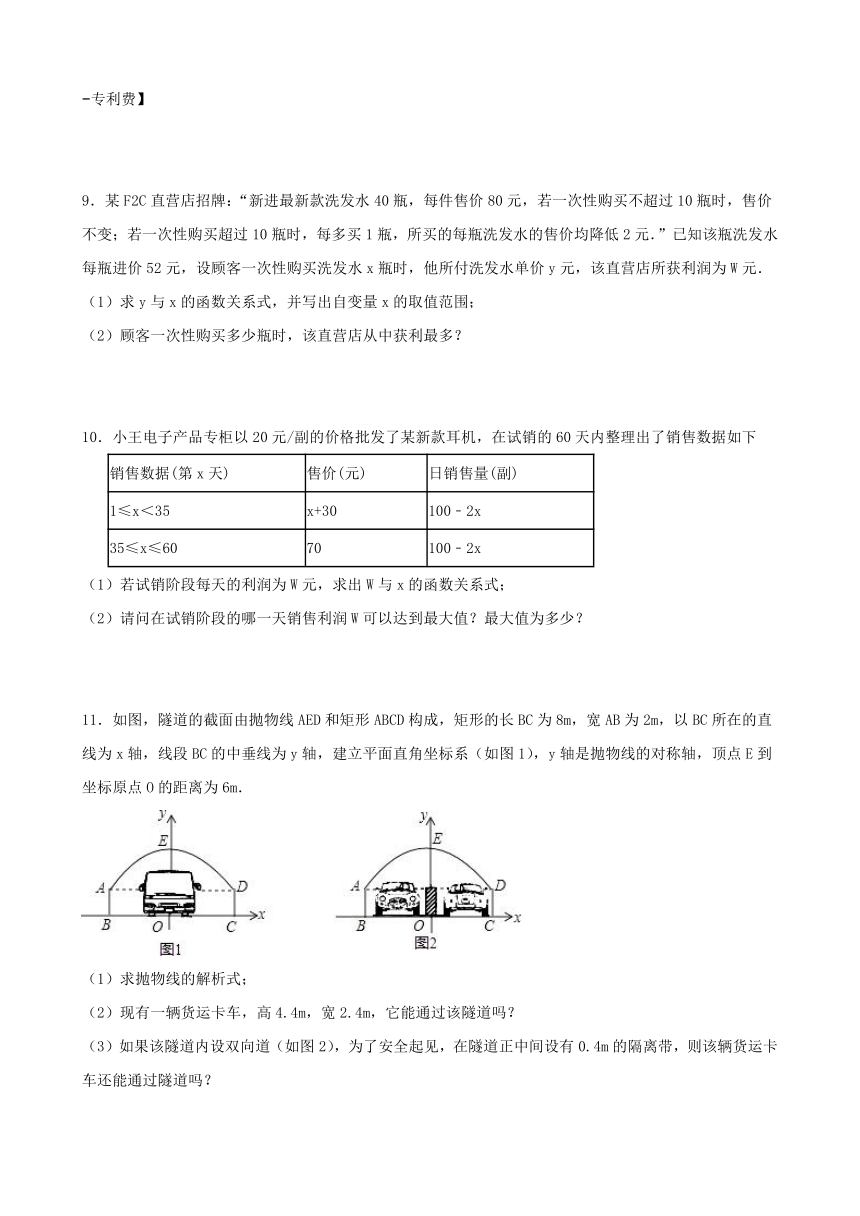
11.如图,隧道的截面由抛物线AED和矩形ABCD构成,矩形的长BC为8m,宽AB为2m,以BC所在的直线为x轴,线段BC的中垂线为y轴,建立平面直角坐标系(如图1),y轴是抛物线的对称轴,顶点E到坐标原点O的距离为6m.
(1)求抛物线的解析式;
(2)现有一辆货运卡车,高4.4m,宽2.4m,它能通过该隧道吗?
(3)如果该隧道内设双向道(如图2),为了安全起见,在隧道正中间设有0.4m的隔离带,则该辆货运卡车还能通过隧道吗?
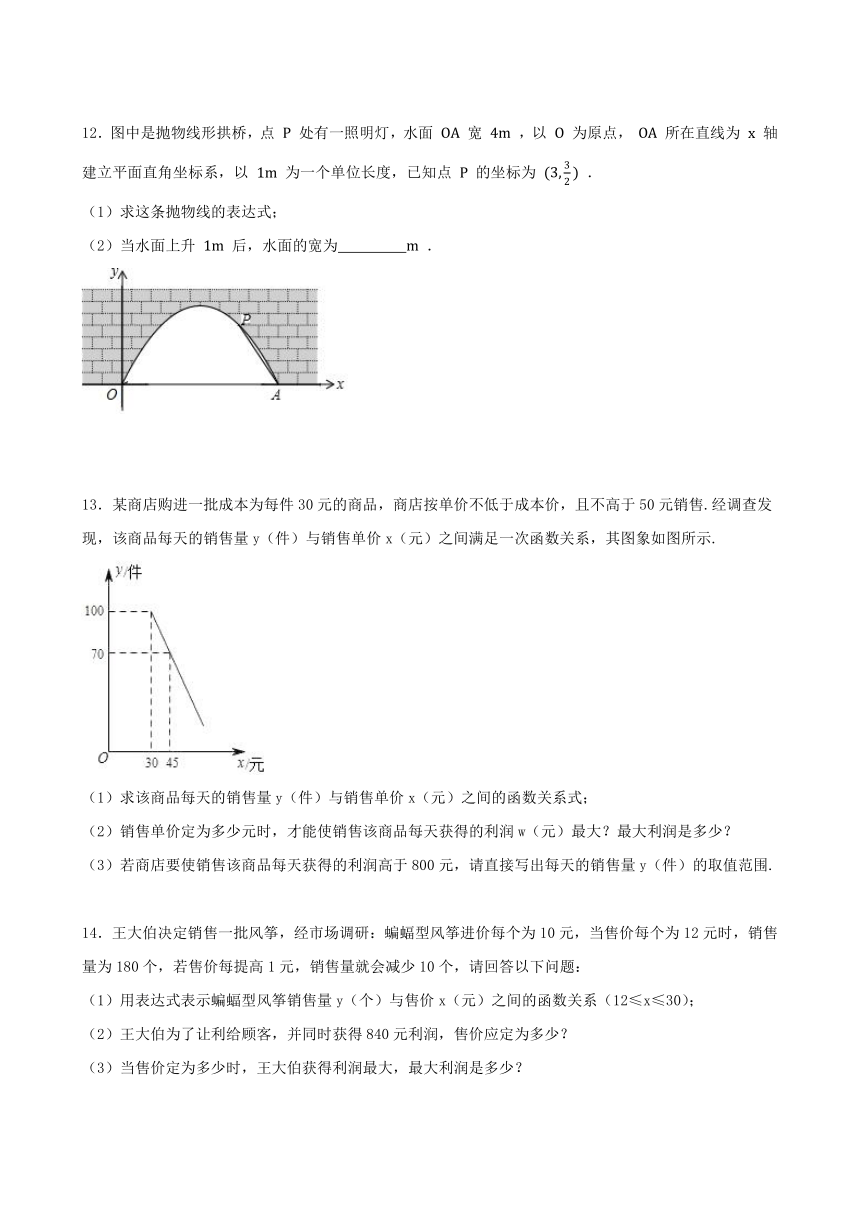
12.图中是抛物线形拱桥,点 处有一照明灯,水面 宽 ,以 为原点, 所在直线为 轴建立平面直角坐标系,以 为一个单位长度,已知点 的坐标为 .
(1)求这条抛物线的表达式;
(2)当水面上升 后,水面的宽为 .
13.某商店购进一批成本为每件30元的商品,商店按单价不低于成本价,且不高于50元销售.经调查发现,该商品每天的销售量y(件)与销售单价x(元)之间满足一次函数关系,其图象如图所示.
(1)求该商品每天的销售量y(件)与销售单价x(元)之间的函数关系式;
(2)销售单价定为多少元时,才能使销售该商品每天获得的利润w(元)最大?最大利润是多少?
(3)若商店要使销售该商品每天获得的利润高于800元,请直接写出每天的销售量y(件)的取值范围.
14.王大伯决定销售一批风筝,经市场调研:蝙蝠型风筝进价每个为10元,当售价每个为12元时,销售量为180个,若售价每提高1元,销售量就会减少10个,请回答以下问题:
(1)用表达式表示蝙蝠型风筝销售量y(个)与售价x(元)之间的函数关系(12≤x≤30);
(2)王大伯为了让利给顾客,并同时获得840元利润,售价应定为多少?
(3)当售价定为多少时,王大伯获得利润最大,最大利润是多少?
15.如图,矩形ABCD的两边长AB=18cm,AD=4cm,点P、Q分别从A、B同时出发,P在边AB上沿AB方向以每秒2cm的速度匀速运动,Q在边BC上沿BC方向以每秒1cm的速度匀速运动,设运动时间为x(秒),△PBQ的面只为y(cm2).
(1)求y关于x的函数关系式,并写出x的取值范围.
(2)求△PBQ的面积的最大值.
16.化工材料经销公司购进一种化工原料若干千克,价格为每千克30元。物价部门规定其销售单价不高于每千克60元,不低于每千克30元。经市场调查发现:日销售量y(千克)是销售单价x(元)的一次函数,且当x=60时,y=80;x=50时,y=100。在销售过程中,每天还要支付其他费用450元。
(1)求出y与x的函数关系式,并写出自变量x的取值范围。
(2)求该公司销售该原料日获利w(元)与销售单价x(元)之间的函数关系式。
(3)当销售单价为多少元时,该公司日获利最大?最大获利是多少元。
17.某公司生产A型活动板房成本是每个425元.图①表示A型活动板房的一面墙,它由长方形和抛物线构成,长方形的长 ,宽 ,抛物线的最高点E到 的距离为 .
(1)按如图①所示的直角坐标系,抛物线可以用 表示,求该抛物线的函数表达式;
(2)现将A型活动板房改造为B型活动板房.如图②,在抛物线与 之间的区域内加装一扇长方形窗户 ,点G,M在 上,点N,F在抛物线上,窗户的成本为50元 .已知 ,求每个 型活动板房的成本是多少?(每个B型活动板房的成本=每个A型活动板房的成本+一扇窗户 的成本)
(3)根据市场调查,以单价650元销售(2)中的 型活动板房,每月能售出100个,而单价每降低10元,每月能多售出20个.公司每月最多能生产160个 型活动板房.不考虑其他因素,公司将销售单价 (元)定为多少时,每月销售 型活动板房所获利润 (元)最大?最大利润是多少?
答案
1.解:(1)∵第一档次的产品一天能生产95件,每件利润6元,每提高一个档次,每件利润加2元,但一天生产量减少5件.
∴第x档次,提高的档次是x﹣1档.
∴y=[6+2(x﹣1)][95﹣5(x﹣1)],
即y=﹣10x2+180x+400(其中x是正整数,且1≤x≤10);
(2)由题意可得:﹣10x2+180x+400=1120
整理得:x2﹣18x+72=0
解得:x1=6,x2=12(舍去).
答:该产品的质量档次为第6档.
2.解:(1)设BC的长度为xm,则AB=(40﹣x),
则矩形区域ABCD的面积y=(40﹣x)=﹣x2+x;
(2)∵y=﹣x2+x=(x﹣20)2+,
∴当x=20时,y有最大值,最大值是m2.
3.(1)解:设y=kx+b,将(30,400),(40,300)代入,得
解得
∴ y=-10x+700.
(2)解:设每日的利润为w元,则w=(x- 20)(-10x+700)=-10x2+900x-14000.
当x= =45元时,W最大=6250元.
4.(1)解:由于抛物线、都过点、,可设它们的解析式为:;
抛物线还经过,
则有:,解得:,
即:抛物线:;
抛物线还经过,
则有:,解得:,
即:抛物线:.
(2)解:当炒菜锅里的水位高度为时,,即,
解得:,
此时水面的直径为.
(3)解:锅盖不能正常盖上,理由如下:
当时,抛物线:,抛物线:,
而,
锅盖不能正常盖上.
5.(1)解:当时,,
整理得:;
当时,,
整理得:;
∴;
(2)解:对于函数,
整理可得:,
∵,
∴当时,取得最大值,最大值为4050;
对于函数,
∵,
∴随的增大而减小,
∵,
∴当时,取得最大值,最大值为3850,
∵,
∴第30天时,当天销售利润最大,最大利润是4050元;
(3)解:当时,由题意,,
解得:或,
由(2)中,二次函数的性质可得:
当时,每天销售利润不低于3250元,共有30天;
当时,由题意,,
解得:,
∴当时,每天销售利润不低于3250元,共有6天;
∴(天),.
∴共有36天每天销售利润不低于3250元.
6.解:(1)由题意得y=500﹣50×,即y=﹣10x+700;(2)由z=100+10y,y=﹣10x+700,得z=﹣100x+7100;(3)w=x(﹣10x+700)﹣(﹣100x+7100)即w=﹣10x2+800x﹣7100,当x=﹣=﹣=40时,景点每日获取的利润最大,w最大===8900(元),答:当门票价格为40元时,景点每日获取的利润最大,最大利润是8900元.
7.(1)解:设,则,∴
(2)解:当y=0时,,解得:,(不合题意,舍去),∴C(13,0)
设第二次落地的抛物线为,则当x=13时,y=0,则,解得:,(不合题意,舍去),
∴
(3)解:当y=0,即
解得:,
(不合题意,舍去),
∴BD=23-6=17(m)
答:运动员乙要抢到第二个落点D,他应再向前跑17m.
8.(1)解:由题意得,,
(2)解:∵,
∴,
∴随x增大而增大,
∴当时,最大,最大为元;
,
∵,
∴当时,随x增大而增大,
∴当时,最大,最大为元;
(3)解:当,即时,该工厂应该选择产销A产品能获得最大日利润;
当,即时,该工厂应该选择产销任一产品都能获得最大日利润;
当,即时,该工厂应该选择产销B产品能获得最大日利润;
综上所述,当时,该工厂应该选择产销A产品能获得最大日利润;当时,该工厂应该选择产销任一产品都能获得最大日利润;当时,该工厂应该选择产销B产品能获得最大日利润.
9.(1)解:根据题意知,当0≤x≤10时,y=80;
当10<x≤24时,y=80﹣2(x﹣10)=﹣2x+100
(2)解:①当0≤x≤10时,W=(80﹣52)x=28x,
∵W随x的增大而增大,
∴当x=10时,W取得最大值,最大值为280;
②当10<x≤24时,W=(﹣2x+100﹣52)x=﹣2(x﹣12)2+288,
∴x=12时,W取得最大值,最大值为288,
综上,当顾客一次性购买12瓶时,该直营店从中获利最多
10.(1)解:①当1≤x<35时,W1=(x+30﹣20)(100﹣2x)
即W1=﹣2(x﹣20)2+1800;
②当35≤2x≤26时,W2=(70﹣20)(100﹣2x)
即W2=﹣100x+5000;
故W与x之间的函数关系式为:
W= ;
(2)解:∵W1=﹣2(x﹣20)2+1800(1≤x<35),
∴在试销的第一阶段,在第20天时,利润最大为1800元,
∵W2=﹣100x+5000(35≤x≤60),
∴在试销的第二阶段,在第35天时,销售利润最大为1500元,
答:在试销阶段的第20天时W最大,最大值为1800元.
11.(1)解:∵OE为线段BC的中垂线,
∴OC= BC.
∵四边形ABCD是矩形,
∴AD=BC=8m,AB=CD=2m,
∴OC=4.
∴D(4,2,).E(0,6).
设抛物线的解析式为y=ax2+c,由题意,得
,
解得: ,
∴y=﹣ x2+6
(2)解:由题意,得
当y=4.4时,4.4=﹣ x2+6,
解得:x=± ,
∴宽度为: >2.4,
∴它能通过该隧道
(3)解:由题意,得
( ﹣0.4)= ﹣0.2>2.4,
∴该辆货运卡车还能通过隧道
12.(1)解:设抛物线的解析式为y=ax2+bx,
将点A(4,0)、P 代入,得: ,
解得: ,
所以抛物线的解析式为y=- x2+2x;
(2)2 .
13.(1)解:设y与销售单价x之间的函数关系式为:y=kx+b,
将点(30,100)、(45,70)代入一次函数表达式得: ,
解得: ,
故函数的表达式为:y=﹣2x+160(30≤x≤50)
(2)解:由题意得:w=(x﹣30)(﹣2x+160)=﹣2(x﹣55)2+1250,
∵﹣2<0,故当x<55时,w随x的增大而增大,而30≤x≤50,
∴当x=50时,w有最大值,此时,w=1200,
故销售单价定为50元时,该超市每天的利润最大,最大利润1200元
(3)解:由题意得:(x﹣30)(﹣2x+160)>800,
解得:40<x<70,
∵30≤x≤50
解得:40<x≤50,当x=40时,y=﹣2×40+160=80; 当x=50时,y=﹣2×50+160=60,
∴60≤y<8
14.(1)解:设蝙蝠型风筝售价为x元时,销售量为y个,
根据题意可知:y=180﹣10(x﹣12)=﹣10x+300(12≤x≤30)
(2)解:设王大伯获得的利润为W,则W=(x﹣10)y=﹣10x2+400x﹣3000,
令W=840,则﹣10x2+400x﹣3000=840,
解得:x1=16,x2=24,
答:王大伯为了让利给顾客,并同时获得840元利润,售价应定为16元
(3)解:∵W=﹣10x2+400x﹣3000=﹣10(x﹣20)2+1000,
∵a=﹣10<0,
∴当x=20时,W取最大值,最大值为1000.
答:当售价定为20元时,王大伯获得利润最大,最大利润是1000元
15.(1)解:∵ = PB BQ,PB=AB﹣AP=18﹣2x,BQ=x,
∴y= x(18﹣2x),
即y= +9x(0<x≤4)
(2)解:由(1)知,y= +9x(0<x≤4),∴y= ,∵当0<x≤ 时,y随x的增大而增大,
而0<x≤4,
∴当x=4时, =20,
即△PBQ的最大面积是20
16.(1)解:设y=kx+b,根据题意得 ,
解得:k=-2,b=200,
∴y=-2x+200(30≤x≤60)
(2)解:W=(x-30)(-2x+200)-450=-2x2+260x-6450=-2(x-65)2+2000
(3)解:W=-2(x-65)2+2000,∵30≤x≤60,由
∴x=60时,w有最大值为1950元,
∴当销售单价为60元时,该公司日获利最大,为1950元
17.(1)解:由题可知D(2,0),E(0,1)
代入到
得
解得
∴抛物线的函数表达式为 ;
(2)解:由题意可知N点与M点的横坐标相同,把x=1代入 ,得y=
∴N(1, )
∴MN= m,
∴S四边形FGMN=GM×MN=2× = ,
则一扇窗户的价格为 ×50=75元
因此每个B型活动板的成本为425+75=500元;
(3)解:根据题意可得w=(n-500)(100+20× )=-2(n-600)2+20000,
∵一个月最多生产160个,
∴100+20× ≤160
解得n≥620
∵-2<0
∴n≥620时,w随n的增大而减小
∴当n=620时,w最大=19200元
1.某工厂生产的某种产品按质量分为10个档次,第1档次(最低档次)的产品一天能生产95件,每件利润6元.每提高一个档次,每件利润增加2元,但一天产量减少5件.
(1)若生产第x档次的产品一天的总利润为y元(其中x为正整数,且1≤x≤10),求出y关于x的函数关系式;
(2)若生产第x档次的产品一天的总利润为1120元,求该产品的质量档次.
2.为了节省材料,某水产养殖户利用水库的岸堤(岸堤足够长)为一边,用总长为40m的围网
在水库中围成了如图所示的①②二块矩形区域.设BC的长度为xm,矩形区域ABCD的面积为
ym2.
(1)求y与x之间的函数关系式;
(2)为何值时,y有最大值?最大值是多少?
3.某童装店购进一批20元/件的童装,由销售经验知,每天的销售量y(件)与销售单价x(元)之间存在如图的一次函数关系.
(1)求y与x之间的函数关系.
(2)当销售单价定为多少时,每天可获得最大利益,最大利润是多少?
4.我们常见的炒菜锅和锅盖都是抛物线面,经过锅心和盖心的纵断面是两段抛物线组合而成封闭图形,不妨简称为“锅线”,锅口直径为,锅深,锅盖高锅口直径与锅盖直径视为相同,建立直角坐标系如图所示,如果把锅纵断面的抛物线记为,把锅盖纵断面的抛物线记为.
(1)求和的解析式;
(2)如果炒菜时锅的水位高度是,求此时水面的直径;
(3)如果将一个底面直径为,高度为的圆柱形器皿放入炒菜锅内蒸食物,锅盖能否正常盖上?请说明理由.
5.九年级数学兴趣小组经过市场调查,整理出某种商品在第(且为整数)天的售价与销量的相关信息如下表:
时间(天)
售价(元/件) 85
每天销量(件)
已知该商品的进价为每件30元,设销售该商品的每天利润为元.
(1)求出与的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少
(3)该商品在销售过程中,共有几天每天销售利润不低于3250元 请直接写出结果.
6.某旅游景点的门票价格是20元/人,日接待游客500人,进入旅游旺季时,景点想提高门票价格增加盈利.经过市场调查发现,门票价格每提高5元,日接待游客人数就会减少50人.设提价后的门票价格为x(元/人)(x>20),日接待游客的人数为y(人).
(1)求y与x(x>20)的函数关系式;
(2)已知景点每日的接待成本为z(元),z与y满足函数关系式:z=100+10y.求z与x的函数关系式;
(3)在(2)的条件下,当门票价格为多少时,景点每日获取的利润最大?最大利润是多少?(利润=门票收入﹣接待成本)
7.如图,足球场上守门员在O处开出一高球,球从离地面1m的A处飞出(A在y轴上),运动员乙在距O点6m的B处发现球在自己头的正上方达到最高点M,距地面约4m高.球第一次落地后又弹起.据试验,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.
解答下列问题: (注意:取,)
(1)求足球开始飞出到第一次落地时,该抛物线的表达式;
(2)求足球第二次飞出到落地时,该抛物线的表达式;
(3)运动员乙要抢到第二个落点D,他应再向前跑多少m?
8.某工厂计划从A,B两种产品中选择一种生产并销售,每日产销x件.已知A产品成本价m元/件(m为常数,且,售价8元/件,每日最多产销500件,同时每日共支付专利费30元;B产品成本价12元/件,售价20元/件,每日最多产销300件,同时每日支付专利费y元,y(元)与每日产销x(件)满足关系式
(1)若产销A,B两种产品的日利润分别为元,元,请分别写出,与x的函数关系式,并写出x的取值范围;
(2)分别求出产销A,B两种产品的最大日利润.(A产品的最大日利润用含m的代数式表示)
(3)为获得最大日利润,该工厂应该选择产销哪种产品?并说明理由.【利润(售价成本)产销数量专利费】
9.某F2C直营店招牌:“新进最新款洗发水40瓶,每件售价80元,若一次性购买不超过10瓶时,售价不变;若一次性购买超过10瓶时,每多买1瓶,所买的每瓶洗发水的售价均降低2元.”已知该瓶洗发水每瓶进价52元,设顾客一次性购买洗发水x瓶时,他所付洗发水单价y元,该直营店所获利润为W元.
(1)求y与x的函数关系式,并写出自变量x的取值范围;
(2)顾客一次性购买多少瓶时,该直营店从中获利最多?
10.小王电子产品专柜以20元/副的价格批发了某新款耳机,在试销的60天内整理出了销售数据如下
销售数据(第x天) 售价(元) 日销售量(副)
1≤x<35 x+30 100﹣2x
35≤x≤60 70 100﹣2x
(1)若试销阶段每天的利润为W元,求出W与x的函数关系式;
(2)请问在试销阶段的哪一天销售利润W可以达到最大值?最大值为多少?
11.如图,隧道的截面由抛物线AED和矩形ABCD构成,矩形的长BC为8m,宽AB为2m,以BC所在的直线为x轴,线段BC的中垂线为y轴,建立平面直角坐标系(如图1),y轴是抛物线的对称轴,顶点E到坐标原点O的距离为6m.
(1)求抛物线的解析式;
(2)现有一辆货运卡车,高4.4m,宽2.4m,它能通过该隧道吗?
(3)如果该隧道内设双向道(如图2),为了安全起见,在隧道正中间设有0.4m的隔离带,则该辆货运卡车还能通过隧道吗?
12.图中是抛物线形拱桥,点 处有一照明灯,水面 宽 ,以 为原点, 所在直线为 轴建立平面直角坐标系,以 为一个单位长度,已知点 的坐标为 .
(1)求这条抛物线的表达式;
(2)当水面上升 后,水面的宽为 .
13.某商店购进一批成本为每件30元的商品,商店按单价不低于成本价,且不高于50元销售.经调查发现,该商品每天的销售量y(件)与销售单价x(元)之间满足一次函数关系,其图象如图所示.
(1)求该商品每天的销售量y(件)与销售单价x(元)之间的函数关系式;
(2)销售单价定为多少元时,才能使销售该商品每天获得的利润w(元)最大?最大利润是多少?
(3)若商店要使销售该商品每天获得的利润高于800元,请直接写出每天的销售量y(件)的取值范围.
14.王大伯决定销售一批风筝,经市场调研:蝙蝠型风筝进价每个为10元,当售价每个为12元时,销售量为180个,若售价每提高1元,销售量就会减少10个,请回答以下问题:
(1)用表达式表示蝙蝠型风筝销售量y(个)与售价x(元)之间的函数关系(12≤x≤30);
(2)王大伯为了让利给顾客,并同时获得840元利润,售价应定为多少?
(3)当售价定为多少时,王大伯获得利润最大,最大利润是多少?
15.如图,矩形ABCD的两边长AB=18cm,AD=4cm,点P、Q分别从A、B同时出发,P在边AB上沿AB方向以每秒2cm的速度匀速运动,Q在边BC上沿BC方向以每秒1cm的速度匀速运动,设运动时间为x(秒),△PBQ的面只为y(cm2).
(1)求y关于x的函数关系式,并写出x的取值范围.
(2)求△PBQ的面积的最大值.
16.化工材料经销公司购进一种化工原料若干千克,价格为每千克30元。物价部门规定其销售单价不高于每千克60元,不低于每千克30元。经市场调查发现:日销售量y(千克)是销售单价x(元)的一次函数,且当x=60时,y=80;x=50时,y=100。在销售过程中,每天还要支付其他费用450元。
(1)求出y与x的函数关系式,并写出自变量x的取值范围。
(2)求该公司销售该原料日获利w(元)与销售单价x(元)之间的函数关系式。
(3)当销售单价为多少元时,该公司日获利最大?最大获利是多少元。
17.某公司生产A型活动板房成本是每个425元.图①表示A型活动板房的一面墙,它由长方形和抛物线构成,长方形的长 ,宽 ,抛物线的最高点E到 的距离为 .
(1)按如图①所示的直角坐标系,抛物线可以用 表示,求该抛物线的函数表达式;
(2)现将A型活动板房改造为B型活动板房.如图②,在抛物线与 之间的区域内加装一扇长方形窗户 ,点G,M在 上,点N,F在抛物线上,窗户的成本为50元 .已知 ,求每个 型活动板房的成本是多少?(每个B型活动板房的成本=每个A型活动板房的成本+一扇窗户 的成本)
(3)根据市场调查,以单价650元销售(2)中的 型活动板房,每月能售出100个,而单价每降低10元,每月能多售出20个.公司每月最多能生产160个 型活动板房.不考虑其他因素,公司将销售单价 (元)定为多少时,每月销售 型活动板房所获利润 (元)最大?最大利润是多少?
答案
1.解:(1)∵第一档次的产品一天能生产95件,每件利润6元,每提高一个档次,每件利润加2元,但一天生产量减少5件.
∴第x档次,提高的档次是x﹣1档.
∴y=[6+2(x﹣1)][95﹣5(x﹣1)],
即y=﹣10x2+180x+400(其中x是正整数,且1≤x≤10);
(2)由题意可得:﹣10x2+180x+400=1120
整理得:x2﹣18x+72=0
解得:x1=6,x2=12(舍去).
答:该产品的质量档次为第6档.
2.解:(1)设BC的长度为xm,则AB=(40﹣x),
则矩形区域ABCD的面积y=(40﹣x)=﹣x2+x;
(2)∵y=﹣x2+x=(x﹣20)2+,
∴当x=20时,y有最大值,最大值是m2.
3.(1)解:设y=kx+b,将(30,400),(40,300)代入,得
解得
∴ y=-10x+700.
(2)解:设每日的利润为w元,则w=(x- 20)(-10x+700)=-10x2+900x-14000.
当x= =45元时,W最大=6250元.
4.(1)解:由于抛物线、都过点、,可设它们的解析式为:;
抛物线还经过,
则有:,解得:,
即:抛物线:;
抛物线还经过,
则有:,解得:,
即:抛物线:.
(2)解:当炒菜锅里的水位高度为时,,即,
解得:,
此时水面的直径为.
(3)解:锅盖不能正常盖上,理由如下:
当时,抛物线:,抛物线:,
而,
锅盖不能正常盖上.
5.(1)解:当时,,
整理得:;
当时,,
整理得:;
∴;
(2)解:对于函数,
整理可得:,
∵,
∴当时,取得最大值,最大值为4050;
对于函数,
∵,
∴随的增大而减小,
∵,
∴当时,取得最大值,最大值为3850,
∵,
∴第30天时,当天销售利润最大,最大利润是4050元;
(3)解:当时,由题意,,
解得:或,
由(2)中,二次函数的性质可得:
当时,每天销售利润不低于3250元,共有30天;
当时,由题意,,
解得:,
∴当时,每天销售利润不低于3250元,共有6天;
∴(天),.
∴共有36天每天销售利润不低于3250元.
6.解:(1)由题意得y=500﹣50×,即y=﹣10x+700;(2)由z=100+10y,y=﹣10x+700,得z=﹣100x+7100;(3)w=x(﹣10x+700)﹣(﹣100x+7100)即w=﹣10x2+800x﹣7100,当x=﹣=﹣=40时,景点每日获取的利润最大,w最大===8900(元),答:当门票价格为40元时,景点每日获取的利润最大,最大利润是8900元.
7.(1)解:设,则,∴
(2)解:当y=0时,,解得:,(不合题意,舍去),∴C(13,0)
设第二次落地的抛物线为,则当x=13时,y=0,则,解得:,(不合题意,舍去),
∴
(3)解:当y=0,即
解得:,
(不合题意,舍去),
∴BD=23-6=17(m)
答:运动员乙要抢到第二个落点D,他应再向前跑17m.
8.(1)解:由题意得,,
(2)解:∵,
∴,
∴随x增大而增大,
∴当时,最大,最大为元;
,
∵,
∴当时,随x增大而增大,
∴当时,最大,最大为元;
(3)解:当,即时,该工厂应该选择产销A产品能获得最大日利润;
当,即时,该工厂应该选择产销任一产品都能获得最大日利润;
当,即时,该工厂应该选择产销B产品能获得最大日利润;
综上所述,当时,该工厂应该选择产销A产品能获得最大日利润;当时,该工厂应该选择产销任一产品都能获得最大日利润;当时,该工厂应该选择产销B产品能获得最大日利润.
9.(1)解:根据题意知,当0≤x≤10时,y=80;
当10<x≤24时,y=80﹣2(x﹣10)=﹣2x+100
(2)解:①当0≤x≤10时,W=(80﹣52)x=28x,
∵W随x的增大而增大,
∴当x=10时,W取得最大值,最大值为280;
②当10<x≤24时,W=(﹣2x+100﹣52)x=﹣2(x﹣12)2+288,
∴x=12时,W取得最大值,最大值为288,
综上,当顾客一次性购买12瓶时,该直营店从中获利最多
10.(1)解:①当1≤x<35时,W1=(x+30﹣20)(100﹣2x)
即W1=﹣2(x﹣20)2+1800;
②当35≤2x≤26时,W2=(70﹣20)(100﹣2x)
即W2=﹣100x+5000;
故W与x之间的函数关系式为:
W= ;
(2)解:∵W1=﹣2(x﹣20)2+1800(1≤x<35),
∴在试销的第一阶段,在第20天时,利润最大为1800元,
∵W2=﹣100x+5000(35≤x≤60),
∴在试销的第二阶段,在第35天时,销售利润最大为1500元,
答:在试销阶段的第20天时W最大,最大值为1800元.
11.(1)解:∵OE为线段BC的中垂线,
∴OC= BC.
∵四边形ABCD是矩形,
∴AD=BC=8m,AB=CD=2m,
∴OC=4.
∴D(4,2,).E(0,6).
设抛物线的解析式为y=ax2+c,由题意,得
,
解得: ,
∴y=﹣ x2+6
(2)解:由题意,得
当y=4.4时,4.4=﹣ x2+6,
解得:x=± ,
∴宽度为: >2.4,
∴它能通过该隧道
(3)解:由题意,得
( ﹣0.4)= ﹣0.2>2.4,
∴该辆货运卡车还能通过隧道
12.(1)解:设抛物线的解析式为y=ax2+bx,
将点A(4,0)、P 代入,得: ,
解得: ,
所以抛物线的解析式为y=- x2+2x;
(2)2 .
13.(1)解:设y与销售单价x之间的函数关系式为:y=kx+b,
将点(30,100)、(45,70)代入一次函数表达式得: ,
解得: ,
故函数的表达式为:y=﹣2x+160(30≤x≤50)
(2)解:由题意得:w=(x﹣30)(﹣2x+160)=﹣2(x﹣55)2+1250,
∵﹣2<0,故当x<55时,w随x的增大而增大,而30≤x≤50,
∴当x=50时,w有最大值,此时,w=1200,
故销售单价定为50元时,该超市每天的利润最大,最大利润1200元
(3)解:由题意得:(x﹣30)(﹣2x+160)>800,
解得:40<x<70,
∵30≤x≤50
解得:40<x≤50,当x=40时,y=﹣2×40+160=80; 当x=50时,y=﹣2×50+160=60,
∴60≤y<8
14.(1)解:设蝙蝠型风筝售价为x元时,销售量为y个,
根据题意可知:y=180﹣10(x﹣12)=﹣10x+300(12≤x≤30)
(2)解:设王大伯获得的利润为W,则W=(x﹣10)y=﹣10x2+400x﹣3000,
令W=840,则﹣10x2+400x﹣3000=840,
解得:x1=16,x2=24,
答:王大伯为了让利给顾客,并同时获得840元利润,售价应定为16元
(3)解:∵W=﹣10x2+400x﹣3000=﹣10(x﹣20)2+1000,
∵a=﹣10<0,
∴当x=20时,W取最大值,最大值为1000.
答:当售价定为20元时,王大伯获得利润最大,最大利润是1000元
15.(1)解:∵ = PB BQ,PB=AB﹣AP=18﹣2x,BQ=x,
∴y= x(18﹣2x),
即y= +9x(0<x≤4)
(2)解:由(1)知,y= +9x(0<x≤4),∴y= ,∵当0<x≤ 时,y随x的增大而增大,
而0<x≤4,
∴当x=4时, =20,
即△PBQ的最大面积是20
16.(1)解:设y=kx+b,根据题意得 ,
解得:k=-2,b=200,
∴y=-2x+200(30≤x≤60)
(2)解:W=(x-30)(-2x+200)-450=-2x2+260x-6450=-2(x-65)2+2000
(3)解:W=-2(x-65)2+2000,∵30≤x≤60,由
∴x=60时,w有最大值为1950元,
∴当销售单价为60元时,该公司日获利最大,为1950元
17.(1)解:由题可知D(2,0),E(0,1)
代入到
得
解得
∴抛物线的函数表达式为 ;
(2)解:由题意可知N点与M点的横坐标相同,把x=1代入 ,得y=
∴N(1, )
∴MN= m,
∴S四边形FGMN=GM×MN=2× = ,
则一扇窗户的价格为 ×50=75元
因此每个B型活动板的成本为425+75=500元;
(3)解:根据题意可得w=(n-500)(100+20× )=-2(n-600)2+20000,
∵一个月最多生产160个,
∴100+20× ≤160
解得n≥620
∵-2<0
∴n≥620时,w随n的增大而减小
∴当n=620时,w最大=19200元
同课章节目录
