安徽省亳州市利辛县部分学校联考2023-2024学年九年级上学期期末数学试题(含答案)
文档属性
| 名称 | 安徽省亳州市利辛县部分学校联考2023-2024学年九年级上学期期末数学试题(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-17 00:00:00 | ||
图片预览



文档简介
九年级数学(沪科版)
(试题卷)
注意事项:
1.你拿到的试卷满分为150分,考试时间为120分钟.
2.试卷包括“试题卷”和“答题卷”两部分,请务必在“答题卷”上答题,在“试题卷”上答题是无效的.
3.考试结束后,请将“试题卷”和“答题卷”一并交回.
一、选择题(本大题共10小题,每小题4分,满分40分)
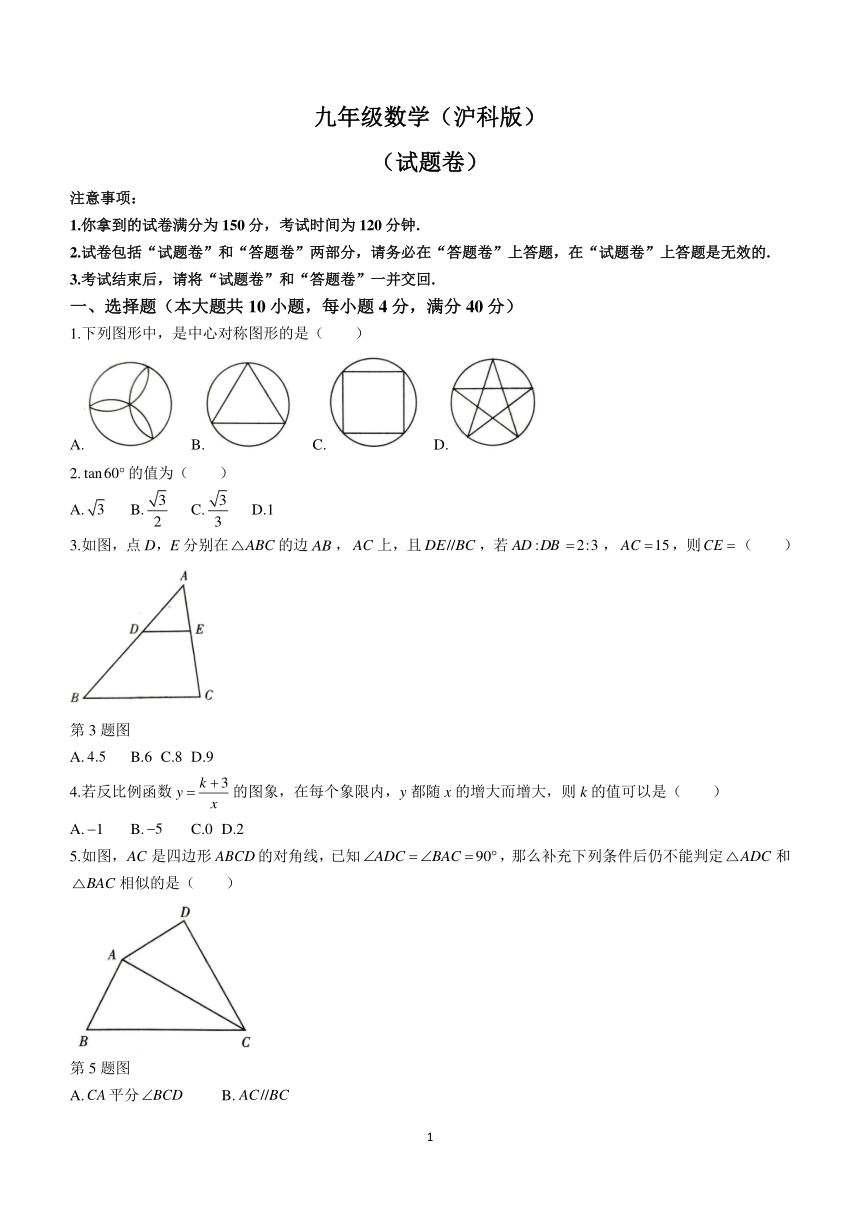
1.下列图形中,是中心对称图形的是( )
A. B. C. D.
2.的值为( )
A. B. C. D.1
3.如图,点D,E分别在的边,上,且,若,,则( )
第3题图
A. B.6 C.8 D.9
4.若反比例函数的图象,在每个象限内,y都随x的增大而增大,则k的值可以是( )
A. B. C.0 D.2
5.如图,是四边形的对角线,已知,那么补充下列条件后仍不能判定和相似的是( )
第5题图
A.平分 B.
C. D.
6.二次函数,若,则自变量x的取值范围是( )
A.或 B.或
C. D.
7.经过坐标原点O,分别与x轴、y轴交于点A、点B,点C是位于第一象限部分上的一点,如图,若点A坐标为,点B坐标为,则的值为( )
第7题图
A. B. C. D.
8.如图,在平行四边形中,点E在边上,,连接交点F,则的周长与的周长之比为( )
第8题图
A. B. C. D.
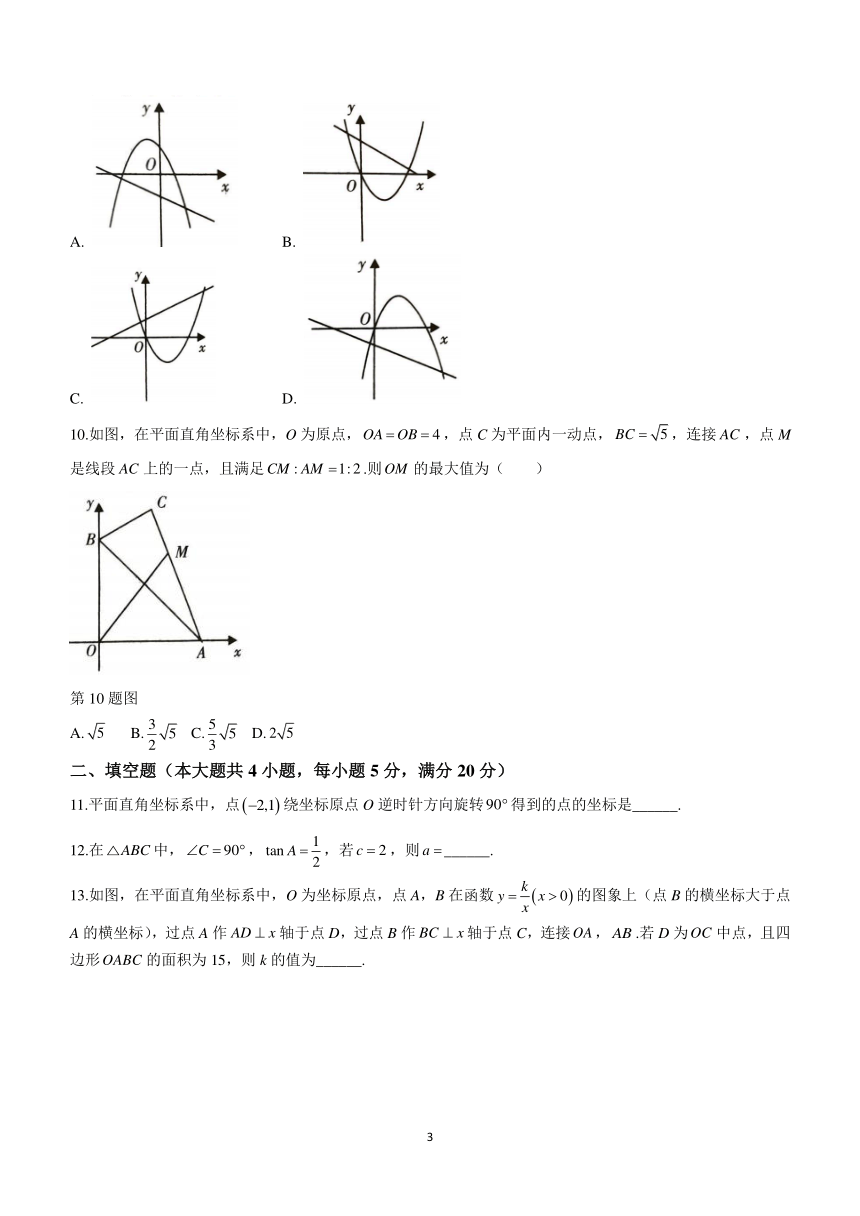
9.已知反比例函数的图象如图所示,则二次函数和一次函数在同一平面直角坐标系中的图象可能是( )
第9题图
A. B.
C. D.
10.如图,在平面直角坐标系中,O为原点,,点C为平面内一动点,,连接,点M是线段上的一点,且满足.则的最大值为( )
第10题图
A. B. C. D.
二、填空题(本大题共4小题,每小题5分,满分20分)
11.平面直角坐标系中,点绕坐标原点O逆时针方向旋转得到的点的坐标是______.
12.在中,,,若,则______.
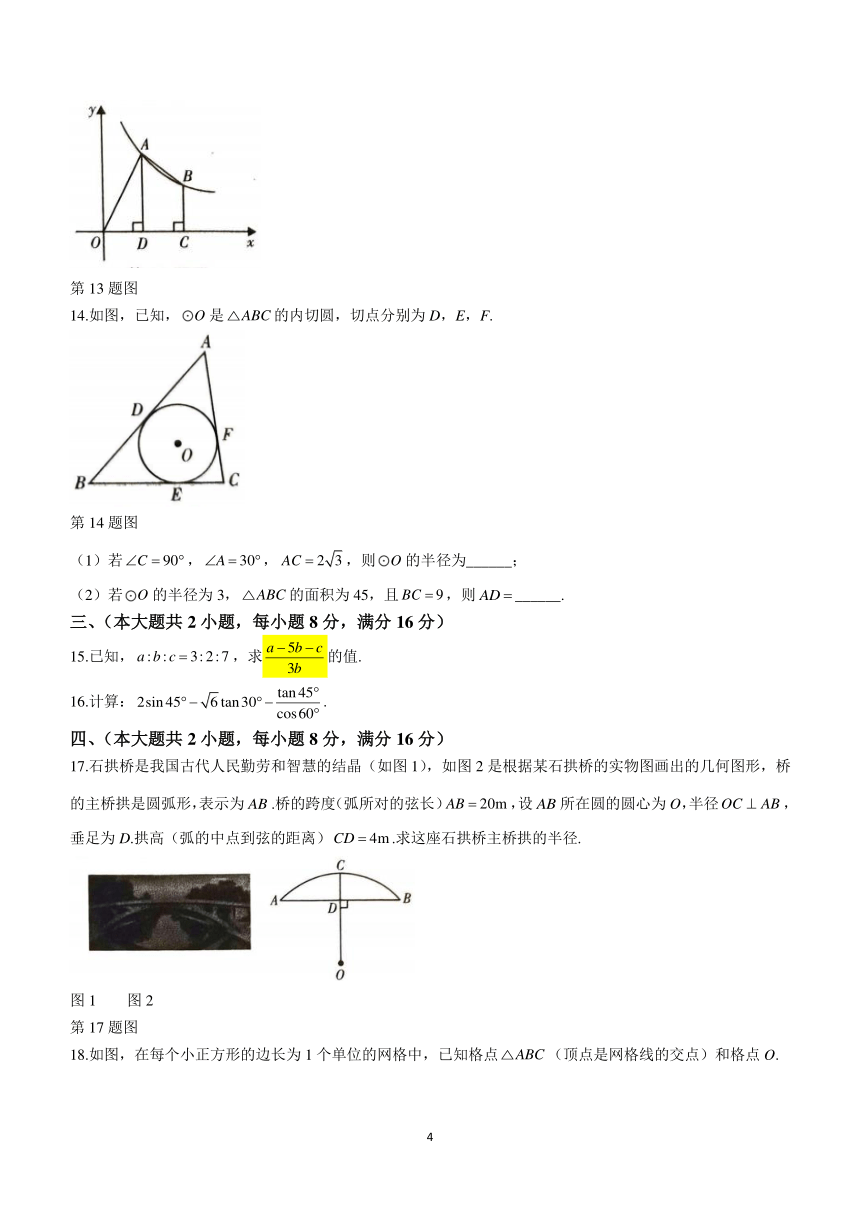
13.如图,在平面直角坐标系中,O为坐标原点,点A,B在函数的图象上(点B的横坐标大于点A的横坐标),过点A作轴于点D,过点B作轴于点C,连接,.若D为中点,且四边形的面积为15,则k的值为______.
第13题图
14.如图,已知,是的内切圆,切点分别为D,E,F.
第14题图
(1)若,,,则的半径为______;
(2)若的半径为3,的面积为45,且,则______.
三、(本大题共2小题,每小题8分,满分16分)
15.已知,,求的值.
16.计算:.
四、(本大题共2小题,每小题8分,满分16分)
17.石拱桥是我国古代人民勤劳和智慧的结晶(如图1),如图2是根据某石拱桥的实物图画出的几何图形,桥的主桥拱是圆弧形,表示为.桥的跨度(弧所对的弦长),设所在圆的圆心为O,半径,垂足为D.拱高(弧的中点到弦的距离).求这座石拱桥主桥拱的半径.
图1 图2
第17题图
18.如图,在每个小正方形的边长为1个单位的网格中,已知格点(顶点是网格线的交点)和格点O.
第18题图
(1)以点O为位似中心,在和点O的另一侧画出,使与位似,且位似比为;
(2)将(1)中的绕点逆时针旋转得到,画出.
五、(本大题共2小题,每小题10分,满分20分)
19.已知,二次函数的图象经过点和.
(1)求b,c的值;
(2)求该函数图象的顶点坐标,并指出x满足什么条件时,y随x的增大而减小.
20.某数学活动小组运用所学的解直角三角形知识测量楼房的楼顶安装的信号发射塔外墙的高度,利用测角仪和米尺等工具进行如下操作:在A处测得,在B处测得,点A、B、C在一条直线上,于点C,于点F,为20米,米,测角仪的高度(、)为1.5米,请根据测量数据,求出信号发射塔的值.
(结果精确到1米,参考数据:,,,)
第20题图
六、(本题满分12分)
21、如图,是的直径,点C在上,点M在外,连接,若.
(1)求证:是的切线;
(2)已知,点D是的中点,过点D作,交于点E,若的半径为10,,求的长.
七、(本题满分12分)
22.如图,与有公共的顶点E,已知,,点D在边上,.
第22题图
(1)求证:;
(2)若平分,,当,时,求的长.
八、(本题满分14分)
23.规定:如果两个函数的图象关于y轴对称,那么称这两个函数“互为Y函数”.例如:函数与“互为Y函数”.
(1)请写出二次函数的“Y函数”(不用说理);
(2)函数与“互为Y函数”,求a的值;
(3)若函数的图象与x轴只有一个交点,求它的“Y函数”图象与x轴的交点坐标.
九年级数学(沪科版)参考答案及评分标准
一、选择题(本大题共10小题,每小题4分,满分40分)
题号 1 2 3 4 5 6 7 8 9 10
答案 C A D B D A B B C D
二、填空题(本大题共4小题,每小题5分,满分20分)
11. 12. 13.12
14.(1);(2)6
解析:(1)如图1,连接,,,
由题意可得,,,设半径为,
∴,∵,
∴四边形为正方形,∴,
又∵,,
∴,,,,
∵,
∴,解得;
(2)如图2,连接,,,,,,
∵,
∴,
∴,
∴,
∴.
图1 图2
三、(本大题共2小题,每小题8分,满分16分)
15.解:∵,∴设,则,,
∴.
16.解:.
四、(本大题共2小题,每小题8分,满分16分)
17.解:连接,设主桥拱半径为,
∵,垂足为D,∴,
,在中,根据勾股定理得,
∴,解得,
∴这座石拱桥主桥拱的半径约为.
18.解:(1)如图所示,即为所求;
(2)如图所示,即为所求.
五、(本大题共2小题,每小题10分,满分20分)
19.解:(1)∵二次函数的图象经过点和,
∴,解得;
(2)由(1)得二次函数表达式为,
∴函数图象的顶点坐标为,
∵,∴抛物线开口向下,∴当时,y随x的增大而减小.
20.解:由题意得:米,(米),
在中,,∴(米),
在中,,∴(米),
∴(米),
∴信号发射塔的高度约为13米.
六、(本题满分12分)
21.解:(1)证明:如图,连接,∵,∴,
∵是的直径,∴,∴,
∵,∴,∴,
∴是的切线;
(2)如图,令与交于点F,过点E作于点G,
∵,∴,∵,,
∴,∵,∴,∴,
∴.在中,∵,,,
∴,,∴,
∵点D是的中点,∴,∴,∴,∴,
∵,∴,∴.
七、(本题满分12分)
22.解:(1)∵,,
,,∴,∵,∴,
∴,即,
∵,∴;
(2)由(1)得,∴,∵,
∴,∴,∵平分,∴,
∵,∴,∵,∴,
∴,∴,,∴,
即,解得,∴.
八、(本题满分14分)
解:(1);
(2)∵函数的“Y函数”为,∴,;
(3)分两种情况:
①当时,函数表达式为,它的图象与x轴都只有一个交点,
它的“Y函数”表达式为,∴它的“Y函数”图象与x轴的交点坐标为;
②当时,此函数为二次函数,
∵二次函数的图象与x轴只有一个交点,
∴关于x的一元二次方程有两个相等的实数根,
∴,解得,
∴二次函数的表达式为,
∴它的“Y函数”表达式为,
令,则,解得,
∴此二次函数的“Y函数”图象与x轴的交点坐标为,
综上,函数的“Y函数”的图象与x轴的交点坐标为或.
(试题卷)
注意事项:
1.你拿到的试卷满分为150分,考试时间为120分钟.
2.试卷包括“试题卷”和“答题卷”两部分,请务必在“答题卷”上答题,在“试题卷”上答题是无效的.
3.考试结束后,请将“试题卷”和“答题卷”一并交回.
一、选择题(本大题共10小题,每小题4分,满分40分)
1.下列图形中,是中心对称图形的是( )
A. B. C. D.
2.的值为( )
A. B. C. D.1
3.如图,点D,E分别在的边,上,且,若,,则( )
第3题图
A. B.6 C.8 D.9
4.若反比例函数的图象,在每个象限内,y都随x的增大而增大,则k的值可以是( )
A. B. C.0 D.2
5.如图,是四边形的对角线,已知,那么补充下列条件后仍不能判定和相似的是( )
第5题图
A.平分 B.
C. D.
6.二次函数,若,则自变量x的取值范围是( )
A.或 B.或
C. D.
7.经过坐标原点O,分别与x轴、y轴交于点A、点B,点C是位于第一象限部分上的一点,如图,若点A坐标为,点B坐标为,则的值为( )
第7题图
A. B. C. D.
8.如图,在平行四边形中,点E在边上,,连接交点F,则的周长与的周长之比为( )
第8题图
A. B. C. D.
9.已知反比例函数的图象如图所示,则二次函数和一次函数在同一平面直角坐标系中的图象可能是( )
第9题图
A. B.
C. D.
10.如图,在平面直角坐标系中,O为原点,,点C为平面内一动点,,连接,点M是线段上的一点,且满足.则的最大值为( )
第10题图
A. B. C. D.
二、填空题(本大题共4小题,每小题5分,满分20分)
11.平面直角坐标系中,点绕坐标原点O逆时针方向旋转得到的点的坐标是______.
12.在中,,,若,则______.
13.如图,在平面直角坐标系中,O为坐标原点,点A,B在函数的图象上(点B的横坐标大于点A的横坐标),过点A作轴于点D,过点B作轴于点C,连接,.若D为中点,且四边形的面积为15,则k的值为______.
第13题图
14.如图,已知,是的内切圆,切点分别为D,E,F.
第14题图
(1)若,,,则的半径为______;
(2)若的半径为3,的面积为45,且,则______.
三、(本大题共2小题,每小题8分,满分16分)
15.已知,,求的值.
16.计算:.
四、(本大题共2小题,每小题8分,满分16分)
17.石拱桥是我国古代人民勤劳和智慧的结晶(如图1),如图2是根据某石拱桥的实物图画出的几何图形,桥的主桥拱是圆弧形,表示为.桥的跨度(弧所对的弦长),设所在圆的圆心为O,半径,垂足为D.拱高(弧的中点到弦的距离).求这座石拱桥主桥拱的半径.
图1 图2
第17题图
18.如图,在每个小正方形的边长为1个单位的网格中,已知格点(顶点是网格线的交点)和格点O.
第18题图
(1)以点O为位似中心,在和点O的另一侧画出,使与位似,且位似比为;
(2)将(1)中的绕点逆时针旋转得到,画出.
五、(本大题共2小题,每小题10分,满分20分)
19.已知,二次函数的图象经过点和.
(1)求b,c的值;
(2)求该函数图象的顶点坐标,并指出x满足什么条件时,y随x的增大而减小.
20.某数学活动小组运用所学的解直角三角形知识测量楼房的楼顶安装的信号发射塔外墙的高度,利用测角仪和米尺等工具进行如下操作:在A处测得,在B处测得,点A、B、C在一条直线上,于点C,于点F,为20米,米,测角仪的高度(、)为1.5米,请根据测量数据,求出信号发射塔的值.
(结果精确到1米,参考数据:,,,)
第20题图
六、(本题满分12分)
21、如图,是的直径,点C在上,点M在外,连接,若.
(1)求证:是的切线;
(2)已知,点D是的中点,过点D作,交于点E,若的半径为10,,求的长.
七、(本题满分12分)
22.如图,与有公共的顶点E,已知,,点D在边上,.
第22题图
(1)求证:;
(2)若平分,,当,时,求的长.
八、(本题满分14分)
23.规定:如果两个函数的图象关于y轴对称,那么称这两个函数“互为Y函数”.例如:函数与“互为Y函数”.
(1)请写出二次函数的“Y函数”(不用说理);
(2)函数与“互为Y函数”,求a的值;
(3)若函数的图象与x轴只有一个交点,求它的“Y函数”图象与x轴的交点坐标.
九年级数学(沪科版)参考答案及评分标准
一、选择题(本大题共10小题,每小题4分,满分40分)
题号 1 2 3 4 5 6 7 8 9 10
答案 C A D B D A B B C D
二、填空题(本大题共4小题,每小题5分,满分20分)
11. 12. 13.12
14.(1);(2)6
解析:(1)如图1,连接,,,
由题意可得,,,设半径为,
∴,∵,
∴四边形为正方形,∴,
又∵,,
∴,,,,
∵,
∴,解得;
(2)如图2,连接,,,,,,
∵,
∴,
∴,
∴,
∴.
图1 图2
三、(本大题共2小题,每小题8分,满分16分)
15.解:∵,∴设,则,,
∴.
16.解:.
四、(本大题共2小题,每小题8分,满分16分)
17.解:连接,设主桥拱半径为,
∵,垂足为D,∴,
,在中,根据勾股定理得,
∴,解得,
∴这座石拱桥主桥拱的半径约为.
18.解:(1)如图所示,即为所求;
(2)如图所示,即为所求.
五、(本大题共2小题,每小题10分,满分20分)
19.解:(1)∵二次函数的图象经过点和,
∴,解得;
(2)由(1)得二次函数表达式为,
∴函数图象的顶点坐标为,
∵,∴抛物线开口向下,∴当时,y随x的增大而减小.
20.解:由题意得:米,(米),
在中,,∴(米),
在中,,∴(米),
∴(米),
∴信号发射塔的高度约为13米.
六、(本题满分12分)
21.解:(1)证明:如图,连接,∵,∴,
∵是的直径,∴,∴,
∵,∴,∴,
∴是的切线;
(2)如图,令与交于点F,过点E作于点G,
∵,∴,∵,,
∴,∵,∴,∴,
∴.在中,∵,,,
∴,,∴,
∵点D是的中点,∴,∴,∴,∴,
∵,∴,∴.
七、(本题满分12分)
22.解:(1)∵,,
,,∴,∵,∴,
∴,即,
∵,∴;
(2)由(1)得,∴,∵,
∴,∴,∵平分,∴,
∵,∴,∵,∴,
∴,∴,,∴,
即,解得,∴.
八、(本题满分14分)
解:(1);
(2)∵函数的“Y函数”为,∴,;
(3)分两种情况:
①当时,函数表达式为,它的图象与x轴都只有一个交点,
它的“Y函数”表达式为,∴它的“Y函数”图象与x轴的交点坐标为;
②当时,此函数为二次函数,
∵二次函数的图象与x轴只有一个交点,
∴关于x的一元二次方程有两个相等的实数根,
∴,解得,
∴二次函数的表达式为,
∴它的“Y函数”表达式为,
令,则,解得,
∴此二次函数的“Y函数”图象与x轴的交点坐标为,
综上,函数的“Y函数”的图象与x轴的交点坐标为或.
同课章节目录
