数学人教A版(2019)选择性必修第二册5.3.2函数的极值 课件(共33张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第二册5.3.2函数的极值 课件(共33张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-16 07:44:14 | ||
图片预览








文档简介
(共33张PPT)
人教A版 选择性必修第二册
第五章 一元函数的导数及其应用
5.3 导数在研究函数中的应用
5.3.2 函数的极值
教学目标
1.借助函数图象,了解函数在某点取得极值的必要条件与充分条件;
2.能利用导数求某些函数的极大值、极小值
3.体会导数与单调性、极值、最大(小)值的关系.
01
复习导入
复习导入
思考:如何用导数的方法判断函数的单调性?
函数的单调性与其导函数正负的关系在某个区间上
(1)如果,那么函数在区间上单调递增;
(2)如果,那么函数在区间上单调递减;
(3)如果在区间上恒有那么函数在区间上是常数函数.
(4)在区间上单调递增,则f ′(x)≥0在(a,b)内恒成立
(5)在区间上单调递减,则f ′(x)≤0在(a,b)内恒成立
情景导入
在用导数研究函数的单调性时,我们发现利用导数的正负可以判断函数的单增减.
如果函数在某些点的导数为0,那么在这些点处函数有什么性质呢?
02
函数的极值
新知探究
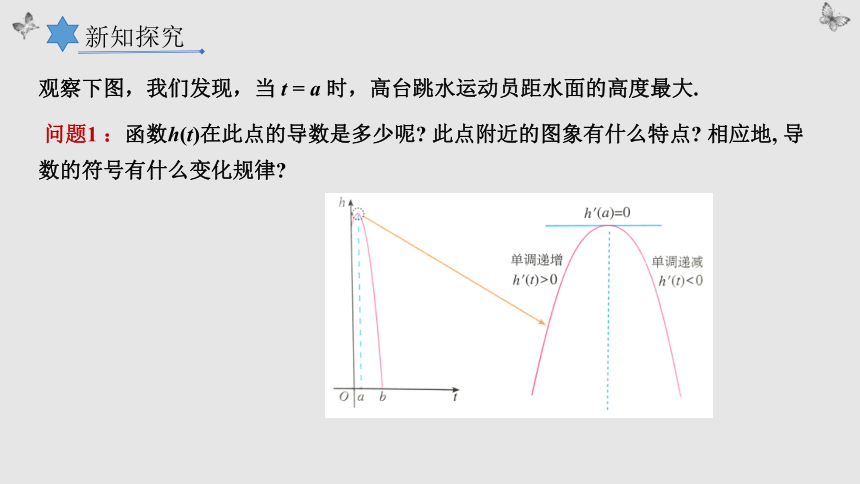
观察下图,我们发现,当 t = a 时,高台跳水运动员距水面的高度最大.
问题1 :函数h(t)在此点的导数是多少呢 此点附近的图象有什么特点 相应地, 导数的符号有什么变化规律
新知探究
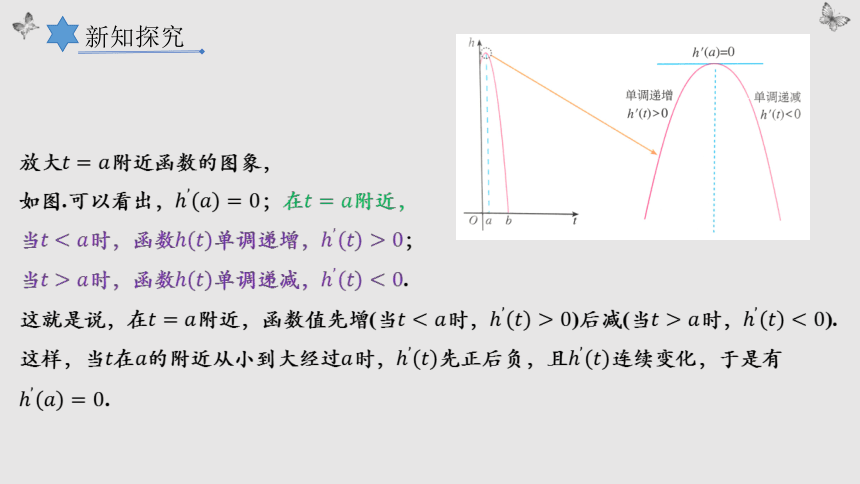
放大附近函数的图象,
如图.可以看出,;在附近,
当时,函数单调递增,;
当时,函数单调递减,.
这就是说,在附近,函数值先增(当时,)后减(当时,).这样,当在的附近从小到大经过时,先正后负,且连续变化,于是有.
新知探究
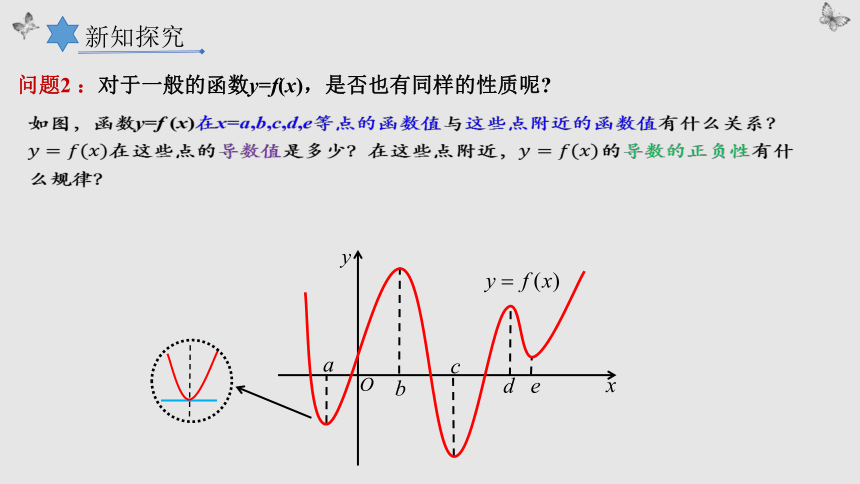
问题2 :对于一般的函数y=f(x),是否也有同样的性质呢
如图,函数y=f (x)在x=a,b,c,d,e等点的函数值与这些点附近的函数值有什么关系?在这些点的导数值是多少?在这些点附近,的导数的正负性有什么规律?
新知探究
以两点为例,可以发现,
①函数在点的函数值比它在点附近其他点的函数值都小,;
②在点附近的左侧,右侧.
③类似地,函数在点的函数值比它在点附近其他点的函数值都大,;
④在点附近的左侧,右侧.
新知探究
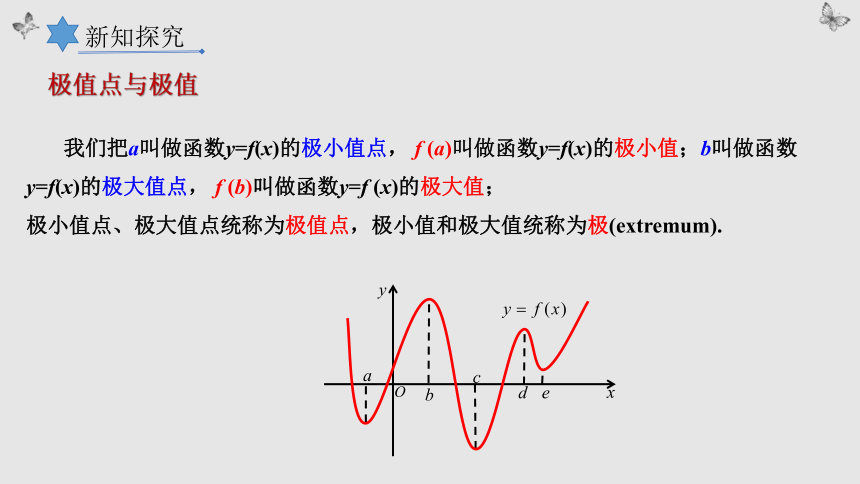
我们把a叫做函数y=f(x)的极小值点, f (a)叫做函数y=f(x)的极小值;b叫做函数y=f(x)的极大值点, f (b)叫做函数y=f (x)的极大值;
极小值点、极大值点统称为极值点,极小值和极大值统称为极(extremum).
极值点与极值
新知探究
x
y
O
y=x3
结论: 若 f ′(x0)=0 ,但 x0不一定是极值点。
思考1:导数为0的点都是极值点吗?
新知探究
思考2: f ′(x0)=0是函数在x=x0处取得极值的什么条件?
结论:f ′(x0)=0 是可导函数在x0处取得极值的必要而不充分条件.
f ′(x0)=0
x0是函数 f(x) 的极值点
x0是函数 f(x) 的极值点
x0左右两侧导数异号
f ′(x0)=0
新知探究
思考3:函数的极大值一定大于极小值吗?
不一定,如图中c处的极小值大于f处的极大值.
新知探究
(3) 极大值与极小值没有必然关系,极大值可能比极小值还小.
(1) 极值是某一点附近的小区间而言的,是函数的局部性质,不是整体的最值;
(2) 函数的极值不一定唯一,在整个定义区间内可能有多个极大值和极小值;
(4) 对于可导函数,若x0是极值点,则 f '(x0)=0;反之,若f '(x0)=0,则x0不一定是极值点.即f ′(x0)=0是函数f(x)在x0处取得极值的必要条件.
关于极值的归纳总结
(5)函数的极值点一定出现在区间的内部,区间的端点不能成为极值点;
(6)单调函数一定没有极值.
新知探究
1.判断下列结论是否正确.(正确的打“√”,错误的打“×”)
(1) 是函数 的极值点.( )
×
(2) 可导函数一定存在极值.( )
×
(3) 若 ,则 是函数 的极值点.( )
×
(4) 若 是函数 的极值点,则 .( )
√
牛刀小试
新知探究
2.已知函数 的定义域为 ,导函数 在 上的图象如图所示,则函数 在 上的极大值点的个数为( ).
B
A. B. C. D.
由导函数的图象可知, 在 上与 轴的交点个数为4,但是在原点附近的导数值恒大于零,故 不是函数 的极值点.其余的3个交点都是极值点,其中有2个点满足其附近的导数值左正右负,故极大值点有2个.
新知探究
例1.求函数的极值.
l
解:因为,所以
令,解得,或.
当变化时,,的变化情况如表所示.
单调递增 单调递减 单调递增
新知探究
因此,当时,有极大值,并且极大值为;
当时,有极小值,并且极小值为;
函数的图象如图所示.
新知探究
问题3 :如何判断f (x0)是极大值或是极小值?
f (x)<0
y
x
O
x1
a
b
y=f(x)
极大值点两侧
极小值点两侧
f (x)<0
f (x)>0
f (x)>0
x2
x x0左侧 x0 x0右侧
f′(x)
f(x)
x x0左侧 x0 x0右侧
f′(x)
f(x)
增
f′(x) >0
f′(x) =0
f′(x) <0
极大值
减
f′(x) <0
f′(x) =0
增
减
极小值
f′(x) >0
左正右负为极大,左负右正为极小
左增右减为极大,左减右增为极小
新知探究
方法总结:求可导函数f (x)极值的步骤:
(1)确定函数的定义域
(2) 求导数f ′(x);
(3)求方程f ′(x)=0的根
(4)由f ′(x)在方程f ′(x)=0的根左右的符号,来判断f (x)在这个根处取极值的情况:
如果左正右负(左增右减),那么f(x)在这个根处取得极大值;
如果左负右正(左减右增),那么f(x)在这个根处取得极小值;
求导—求临界点—列表—求极值
03
极值的简单应用
新知探究
题型一:极值的图象特征
例1.已知函数,其导函数的图象如图所示,则 ( ).
A.在上为减函数
B.在处取极小值
C.在上为减函数
D.在处取极大值
解:由导函数的图象可知:时,;
时,,
因此在,上为增函数,在,上为减函数,
∴函数在处取得极大值,处取得极小值,处取得极大值
C
新知探究
A
新知探究
题型二:求不含参数的函数极值问题
新知探究
新知探究
新知探究
题型三 求含参数的函数的极值
新知探究
新知探究
题型四 已知极值(点)求参数
新知探究
04
课堂小结
课堂小结
人教A版 选择性必修第二册
第五章 一元函数的导数及其应用
5.3 导数在研究函数中的应用
5.3.2 函数的极值
教学目标
1.借助函数图象,了解函数在某点取得极值的必要条件与充分条件;
2.能利用导数求某些函数的极大值、极小值
3.体会导数与单调性、极值、最大(小)值的关系.
01
复习导入
复习导入
思考:如何用导数的方法判断函数的单调性?
函数的单调性与其导函数正负的关系在某个区间上
(1)如果,那么函数在区间上单调递增;
(2)如果,那么函数在区间上单调递减;
(3)如果在区间上恒有那么函数在区间上是常数函数.
(4)在区间上单调递增,则f ′(x)≥0在(a,b)内恒成立
(5)在区间上单调递减,则f ′(x)≤0在(a,b)内恒成立
情景导入
在用导数研究函数的单调性时,我们发现利用导数的正负可以判断函数的单增减.
如果函数在某些点的导数为0,那么在这些点处函数有什么性质呢?
02
函数的极值
新知探究
观察下图,我们发现,当 t = a 时,高台跳水运动员距水面的高度最大.
问题1 :函数h(t)在此点的导数是多少呢 此点附近的图象有什么特点 相应地, 导数的符号有什么变化规律
新知探究
放大附近函数的图象,
如图.可以看出,;在附近,
当时,函数单调递增,;
当时,函数单调递减,.
这就是说,在附近,函数值先增(当时,)后减(当时,).这样,当在的附近从小到大经过时,先正后负,且连续变化,于是有.
新知探究
问题2 :对于一般的函数y=f(x),是否也有同样的性质呢
如图,函数y=f (x)在x=a,b,c,d,e等点的函数值与这些点附近的函数值有什么关系?在这些点的导数值是多少?在这些点附近,的导数的正负性有什么规律?
新知探究
以两点为例,可以发现,
①函数在点的函数值比它在点附近其他点的函数值都小,;
②在点附近的左侧,右侧.
③类似地,函数在点的函数值比它在点附近其他点的函数值都大,;
④在点附近的左侧,右侧.
新知探究
我们把a叫做函数y=f(x)的极小值点, f (a)叫做函数y=f(x)的极小值;b叫做函数y=f(x)的极大值点, f (b)叫做函数y=f (x)的极大值;
极小值点、极大值点统称为极值点,极小值和极大值统称为极(extremum).
极值点与极值
新知探究
x
y
O
y=x3
结论: 若 f ′(x0)=0 ,但 x0不一定是极值点。
思考1:导数为0的点都是极值点吗?
新知探究
思考2: f ′(x0)=0是函数在x=x0处取得极值的什么条件?
结论:f ′(x0)=0 是可导函数在x0处取得极值的必要而不充分条件.
f ′(x0)=0
x0是函数 f(x) 的极值点
x0是函数 f(x) 的极值点
x0左右两侧导数异号
f ′(x0)=0
新知探究
思考3:函数的极大值一定大于极小值吗?
不一定,如图中c处的极小值大于f处的极大值.
新知探究
(3) 极大值与极小值没有必然关系,极大值可能比极小值还小.
(1) 极值是某一点附近的小区间而言的,是函数的局部性质,不是整体的最值;
(2) 函数的极值不一定唯一,在整个定义区间内可能有多个极大值和极小值;
(4) 对于可导函数,若x0是极值点,则 f '(x0)=0;反之,若f '(x0)=0,则x0不一定是极值点.即f ′(x0)=0是函数f(x)在x0处取得极值的必要条件.
关于极值的归纳总结
(5)函数的极值点一定出现在区间的内部,区间的端点不能成为极值点;
(6)单调函数一定没有极值.
新知探究
1.判断下列结论是否正确.(正确的打“√”,错误的打“×”)
(1) 是函数 的极值点.( )
×
(2) 可导函数一定存在极值.( )
×
(3) 若 ,则 是函数 的极值点.( )
×
(4) 若 是函数 的极值点,则 .( )
√
牛刀小试
新知探究
2.已知函数 的定义域为 ,导函数 在 上的图象如图所示,则函数 在 上的极大值点的个数为( ).
B
A. B. C. D.
由导函数的图象可知, 在 上与 轴的交点个数为4,但是在原点附近的导数值恒大于零,故 不是函数 的极值点.其余的3个交点都是极值点,其中有2个点满足其附近的导数值左正右负,故极大值点有2个.
新知探究
例1.求函数的极值.
l
解:因为,所以
令,解得,或.
当变化时,,的变化情况如表所示.
单调递增 单调递减 单调递增
新知探究
因此,当时,有极大值,并且极大值为;
当时,有极小值,并且极小值为;
函数的图象如图所示.
新知探究
问题3 :如何判断f (x0)是极大值或是极小值?
f (x)<0
y
x
O
x1
a
b
y=f(x)
极大值点两侧
极小值点两侧
f (x)<0
f (x)>0
f (x)>0
x2
x x0左侧 x0 x0右侧
f′(x)
f(x)
x x0左侧 x0 x0右侧
f′(x)
f(x)
增
f′(x) >0
f′(x) =0
f′(x) <0
极大值
减
f′(x) <0
f′(x) =0
增
减
极小值
f′(x) >0
左正右负为极大,左负右正为极小
左增右减为极大,左减右增为极小
新知探究
方法总结:求可导函数f (x)极值的步骤:
(1)确定函数的定义域
(2) 求导数f ′(x);
(3)求方程f ′(x)=0的根
(4)由f ′(x)在方程f ′(x)=0的根左右的符号,来判断f (x)在这个根处取极值的情况:
如果左正右负(左增右减),那么f(x)在这个根处取得极大值;
如果左负右正(左减右增),那么f(x)在这个根处取得极小值;
求导—求临界点—列表—求极值
03
极值的简单应用
新知探究
题型一:极值的图象特征
例1.已知函数,其导函数的图象如图所示,则 ( ).
A.在上为减函数
B.在处取极小值
C.在上为减函数
D.在处取极大值
解:由导函数的图象可知:时,;
时,,
因此在,上为增函数,在,上为减函数,
∴函数在处取得极大值,处取得极小值,处取得极大值
C
新知探究
A
新知探究
题型二:求不含参数的函数极值问题
新知探究
新知探究
新知探究
题型三 求含参数的函数的极值
新知探究
新知探究
题型四 已知极值(点)求参数
新知探究
04
课堂小结
课堂小结
