数学人教A版(2019)选择性必修第三册8.1成对数据的统计相关性 课件(共33张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第三册8.1成对数据的统计相关性 课件(共33张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 6.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-16 07:45:55 | ||
图片预览








文档简介
(共33张PPT)
我们已学习了:
单个变量的观察数据的直观表示和统计特征的刻画等知识与方法,如:
用直方图描述样本数据的分布规律
用均值刻画样本数据的集中趋势
用方差刻画样本数据的离散程度……
在现实中,我们还经常需要了解两个或两个以上变量之间的关系,如:
成年子女身高和父母身高之间的关系;
青少年使用手机时长和近视的关系;
高中生数学成绩和物理成绩的关系;
某城市空气污染指数和燃油汽车数量的关系……
推断变量之间关系的知识和方法
选修三 《第八章 成对数据的统计分析》
8.1 成对数据的统计相关性
选修三 《第八章 成对数据的统计分析》
8.1.1变量间的相关关系
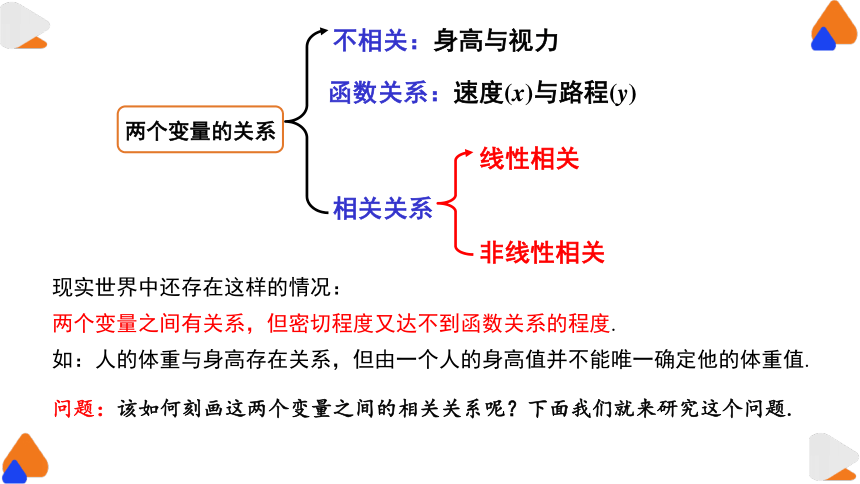
现实世界中还存在这样的情况:
两个变量之间有关系,但密切程度又达不到函数关系的程度.
如:人的体重与身高存在关系,但由一个人的身高值并不能唯一确定他的体重值.
两个变量的关系
不相关:身高与视力
相关关系
函数关系:速度(x)与路程(y)
线性相关
非线性相关
问题:该如何刻画这两个变量之间的相关关系呢?下面我们就来研究这个问题.
1.变量间的相关关系
一个人的体重与他的身高有关系.
一般而言,个子高的人往往体重值较大,个子矮的人往往体重值较小.
但身高并不是体重的唯一决定因素,例如:生活中的饮食习惯、体育锻炼、睡眠时间以及遗传因素等也是影响体重的重要因素.
两个变量有关系,但又没有确切到可由其中的一个去精确地决定另一个的程度,这种关系称为相关关系.
生活中具有相关关系的变量
【子女身高y与父亲身高x之间的关系】一般来说,父亲的个子高(矮),其子女的个子也会比较高(矮);但影响子女身高的因素,除父亲身高外还有其他因素,例如母亲身高、饮食结构、体育锻炼等,因此父亲身高又不能完全决定子女身高.
【商品销售收入y与广告支出x之间的关系】一般来说,广告支出越多,商品销售收入越高,但广告支出并不是决定商品销售收入的唯一因素,商品销售收入还与产品质量、居民收入等因素有关.
生活中具有相关关系的变量
【空气污染指数y与汽车保有量x之间的关系】一般来说,汽车保有量增加,空气污染指数会上升;但汽车保有量并不是造成空气污染的唯一因素,气象条件、工业生产排放、居民生活和取暖、垃圾焚烧等都是影响空气污染指数的因素.
【粮食亩产量y与施肥量x之间的关系】在一定范围内,施肥量越大,粮食亩产量就越高;但施肥量并不是决定粮食亩产量的唯一因素,粮食亩产量还要受到土壤质量、降水量、田间管理水平等因素的影响.
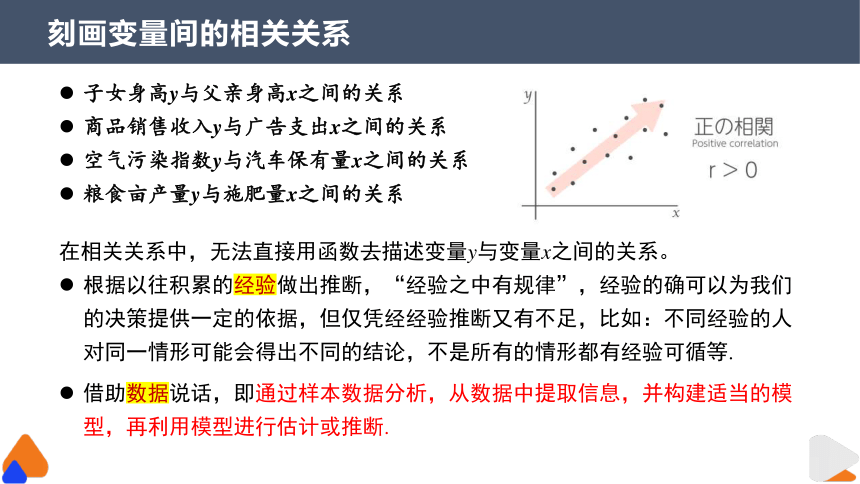
刻画变量间的相关关系
子女身高y与父亲身高x之间的关系
商品销售收入y与广告支出x之间的关系
空气污染指数y与汽车保有量x之间的关系
粮食亩产量y与施肥量x之间的关系
在相关关系中,无法直接用函数去描述变量y与变量x之间的关系。
根据以往积累的经验做出推断,“经验之中有规律”,经验的确可以为我们的决策提供一定的依据,但仅凭经经验推断又有不足,比如:不同经验的人对同一情形可能会得出不同的结论,不是所有的情形都有经验可循等.
借助数据说话,即通过样本数据分析,从数据中提取信息,并构建适当的模型,再利用模型进行估计或推断.
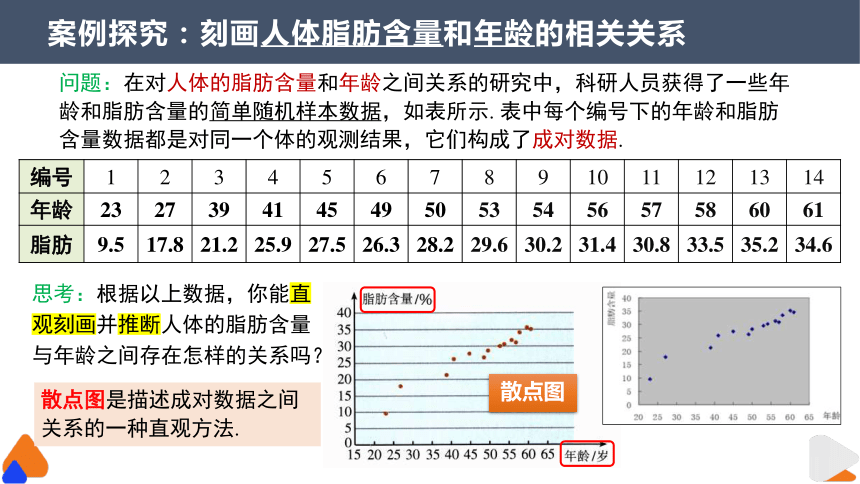
案例探究:刻画人体脂肪含量和年龄的相关关系
问题:在对人体的脂肪含量和年龄之间关系的研究中,科研人员获得了一些年龄和脂肪含量的简单随机样本数据,如表所示. 表中每个编号下的年龄和脂肪含量数据都是对同一个体的观测结果,它们构成了成对数据.
编号 1 2 3 4 5 6 7 8 9 10 11 12 13 14
年龄 23 27 39 41 45 49 50 53 54 56 57 58 60 61
脂肪 9.5 17.8 21.2 25.9 27.5 26.3 28.2 29.6 30.2 31.4 30.8 33.5 35.2 34.6
思考:根据以上数据,你能直观刻画并推断人体的脂肪含量与年龄之间存在怎样的关系吗?
散点图
散点图是描述成对数据之间关系的一种直观方法.
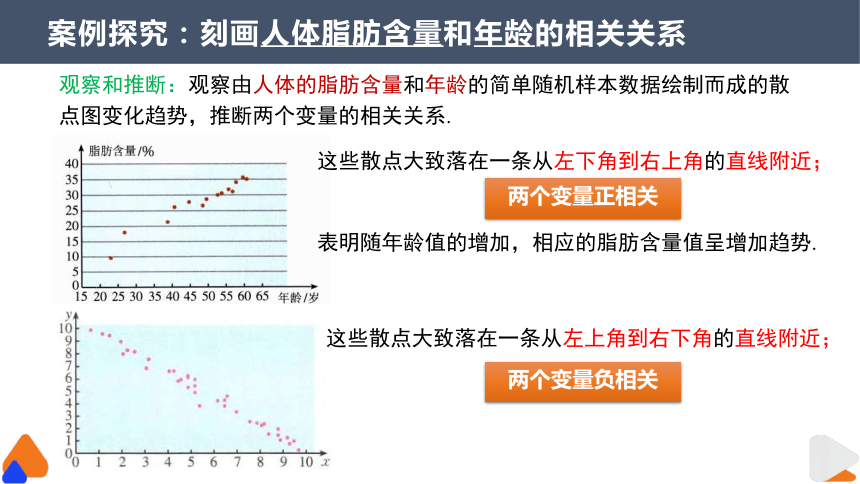
案例探究:刻画人体脂肪含量和年龄的相关关系
观察和推断:观察由人体的脂肪含量和年龄的简单随机样本数据绘制而成的散点图变化趋势,推断两个变量的相关关系.
两个变量正相关
这些散点大致落在一条从左下角到右上角的直线附近;
表明随年龄值的增加,相应的脂肪含量值呈增加趋势.
这些散点大致落在一条从左上角到右下角的直线附近;
两个变量负相关
2.变量间相关关系的类型
从整体上看,
当一个变量的值增加时,另一个变量的相应值也呈现增加的趋势,
则称两个变量正相关;
当一个变量的值增加时,另一个变量的相应值呈现减小的趋势,
则称这两个变量负相关.
如果两个变量的取值呈现正相关或负相关,而且散点落在一条直线附近,则称这两个变量线性相关.
线性相关
非线性相关
(曲线相关)
2.变量间相关关系的类型
散点杂乱无章,无规律可言,看不出两个变量有什么相关性
有相关性
观察散点图中成对样本数据的分布规律,可大致推断两个变量是否存在相关关系、是正相关还是负相关、是线性相关还是非线性相关等.
散点图虽然直观,但无法确切(量化)地反映成对样本数据的相关类型和相关程度的大小.
形
数
思考1:能否引入一个适当的“数字特征”,来度量样本数据是正相关还是负相关呢?
选修三 《第八章 成对数据的统计分析》
8.1.2样本相关系数
探究1:正相关和负相关的定量分析
设变量和经过随机抽样获得的成对样本数据为,,
其中,,,和,,,的均值分别为和.
将数据以为原点进行平移,得到平移后的成对数据为,
,,,并绘制散点图.
若变量x和y 正相关,则关于均值平移后的大多数散点将分布在第一、三象限,对应的成对数据同号的居多,即和同号
若变量x和y 负相关,则关于均值平移后的大多数散点将分布在第二、四象限,对应的成对数据异号的居多,即和异号
平移
形
数
探究2:相关程度大小的定量分析
思考2:Lxy的大小一定能度量出成对样本数据的相关程度大小吗?
是不是Lxy越大,两个变量的相关程度越强?
Lxy>0表明成对样本数据正相关;Lxy<0表明成对样本数据负相关.
Lxy的大小与数据的度量得有关,如:在研究体重与身高之间的相关程度时,如果体重的单位不变,把身高的单位由米改为厘米,则相应的Lxy将变为原来的100倍,即(Lxy)2>(Lxy)1,但单位的改变并不会导致体重与身高之间相关程度的改变.
不宜直接用Lxy度量成对样本数据相关程度的大小.
为了消除度量单位的影响,需要对数据作进一步的“标准化”处理.
形
数
Bug:Lxy的大小受数据的度量单位的影响,但单位的改变并不会导致两个变量之间相关程度的改变.
探究2:相关程度大小的定量分析
为了消除度量单位的影响,需要对数据作进一步的“标准化”处理.
称r为变量x和变量y的样本(线性)相关系数.
新知:样本(线性)相关系数r
①r的正负:反映成对样本数据的变化趋势
变量x和变量y的样本(线性)相关系数:
思考3:r的大小能否刻画成对样本数据的相关程度的强弱?r的取值范围是什么?
强
强
弱
弱
探究3:样本相关系数r的取值范围
观察r的结构,联想到二维(平面)向量、三维(空间)向量数量积的坐标表示,
我们将向量的维数推广到n维,
n维向量的数量积仍定义为:,其中θ为向量的夹角.
n维向量的数量积的坐标表示仍为:若和,
则.
新知:样本(线性)相关系数r
①r的正负:反映成对样本数据的变化趋势
变量x和变量y的样本(线性)相关系数:
②r的范围: 1≤r≤1
探究4:|r|=1时成对样本数据的关系
思考4:当|r|=1时,成对样本数据之间具有怎样的关系呢?
即此时两个变量之间满足一种线性(函数)关系,即满足完全线性相关.
故|r|越接近1时,线性相关程度越强;
|r|越接近0时,线性相关程度越弱;
若所有样本点(xi,yi)
(i=1,2,…,n)都在直线y=-2x+1上,则这组样本数据的样本相关系数为( )
①r的正负:反映成对样本数据的变化趋势
变量x和变量y的样本(线性)相关系数:
②r的范围: 1≤r≤1
③|r|的大小:反映成对样本数据线性相关的程度(即散点集中于某条直线的程度):
|r|越接近1:线性相关程度越强;
|r|越接近0:线性相关程度越弱.
r=0时,只表明成对样本数据间无线性相关关系,但不排除它们有其他相关关系.
④样本容量越大,用样本相关系数估计两个变量的相关系数的效果越好.
r=0.97
r=-0.85
r=0.24
r=-0.05
正线性相关程度很强
负线性相关程度较强
正线性相关程度很弱
负线性相关程度极弱
①r的正负:反映成对样本数据的变化特征
②r的范围: 1≤r≤1
③|r|的大小:反映成对样本数据间线性相关的程度(即散点集中于一条直线的程度):
当|r|越接近1时,线性相关程度越强;当|r|越接近0时,线性相关程度越弱.
新知:样本(线性)相关系数r
新知:样本(线性)相关系数r
如:要确切了解脂肪含量y与年龄x的线性相关程度,需要调查所有人的年龄及其脂肪含量,再将得到的成对数据代入r的公式,计算出相关系数r.
在实际中,获得总体中所有的成对数据往往是不容易的.
在有限的总体中,可以利用这两个变量取值的所有成对数据,通过上述公式就可计算出两个变量的相关系数,这个相关系数就能确切地反映变量之间相关关系的正负性及线性相关程度的强弱.
通过抽样获取两个变量的一些成对样本数据,再计算出样本相关系数,通过样本相关系数去估计总体相关系数,从而了解两个变量之间的相关程度.
思想:用样本估计总体
样本容量越大,用样本相关系数估计两个变量的相关系数的效果越好.
例题点拨
例1.根据表中脂肪含量和年龄的样本数据,推断两个变量是否线性相关,计算样本相关系数,并推断它们的相关程度.
编号 1 2 3 4 5 6 7 8 9 10 11 12 13 14
年龄 23 27 39 41 45 49 50 53 54 56 57 58 60 61
脂肪 9.5 17.8 21.2 25.9 27.5 26.3 28.2 29.6 30.2 31.4 30.8 33.5 35.2 34.6
解:先画出散点图,如图所示.
观察散点图,可看出样本点都集中在一条直线附近,由此推断脂肪含量和年龄线性相关.
代入公式可得样本相关系数r≈0.97,可以推断脂肪含量和年龄这两个变量正线性相关,且相关程度很强.
练习巩固
练习.有一个同学家开了一个小卖部,他为了研究气温对热饮料销售的影响,经过统计,得到一个卖出的热饮杯数与当天气温的数据的散点图和对比表.
解:观察散点图,可看出样本点都集中在一条直线附近,由此推断脂肪含量和年龄线性相关.
代入公式可得样本相关系数r≈﹣0.97,可以推断脂肪含量和年龄这两个变量的负线性相关程度很强.
摄氏温度x -5 4 7 10 15 23 30 36
热饮杯数y 162 128 115 135 89 71 63 37
画出散点图,并用相关系数r判断热饮杯数与当天气温的关系的强弱.
例题点拨
例3.在某校高一年级中随机抽取25名男生,测得他们的身高、体重、臂展等数据,如下表所示.体重与身高、臂展与身高分别具有怎样的相关性?
解:先画出散点图,如图所示.
从散点图看,两个散点图都呈现出线性相关.
通过计算得到体重与身高、臂展与身高的样本相关系数分别约为0.34和0.78,都为正线性相关.
r1≈0.34
∵r2>r1,∴臂展与身高的相关程度更高.
r2≈0.78
【注】在作图中,由于存在误差,有时很难判断这些点是否分布在一条直线的附近,从而就很难判断两个变量之间是否具有线性相关关系,此时就必须利用线性相关系数来判断.
例题点拨
例2.有人收集了某城市居民年收入(所有居民在一年内收入得总和)与A商品销售额的10年数据,如表所示.
画出散点图,推断成对样本数据是否线性相关,并通过样本相关系数推断居民年收入与A商品销售额的相关程度和变化趋势的异同.
解:先画出散点图,如图所示.
从散点图看,A商品销售额与居民年收入的样本数据呈现出线性相关关系.
代入公式可得样本相关系数r≈0.95,A商品销售额与居民年收入正线性相关,即A商品销售额与居民年收入有相同的变化趋势,且相关程度很强.
实际理解与运用
P104-3.根据物理中的胡克定律,弹簧伸长的长度与所受的外力成正比.
测得一根弹簧伸长长度x和相应所受外力F的一组数据如下:
两个变量的样本相关系数是否为1 若不是,请你解释其中的原因.
析:计算可得r≈0.9997
由此可得,弹簧伸长长度x和相应所受外力F几乎完全正线性相关,
样本数据没有完全正线性相关,跟测量存在误差、弹簧制造工艺等因素有关.
实际理解与运用
P104-4.某地区的环境条件适合天鹅栖息繁衍.有人发现了一个有趣的现象:该地区有5个村庄,其中3个村庄附近栖息的天鹅较多,婴儿出生率也较高;2个村庄附近栖息的天鹅较少,婴儿的出生率也较低.
有人认为婴儿出生率和天鹅数之间存在相关关系,并得出一个
结论:天鹅能够带来孩子. 你同意这个结论吗 为什么
从5对统计数据看,婴儿出生率和天鹅数正相关.
但样本数据较少,得出上述结论的可靠性不高。
天鹅数多的地方,婴儿出生率也高,可能是受其他因素的影响,如 :某个村庄生态环境好,适合人类居住,有利于婴儿出生,也适合天鹅栖息繁衍,∴天鹅数多不是婴儿出生率高的原因。
函数关系是一种因果关系;
相关关系不一定是因果关系,也可能是伴随关系.
END
我们已学习了:
单个变量的观察数据的直观表示和统计特征的刻画等知识与方法,如:
用直方图描述样本数据的分布规律
用均值刻画样本数据的集中趋势
用方差刻画样本数据的离散程度……
在现实中,我们还经常需要了解两个或两个以上变量之间的关系,如:
成年子女身高和父母身高之间的关系;
青少年使用手机时长和近视的关系;
高中生数学成绩和物理成绩的关系;
某城市空气污染指数和燃油汽车数量的关系……
推断变量之间关系的知识和方法
选修三 《第八章 成对数据的统计分析》
8.1 成对数据的统计相关性
选修三 《第八章 成对数据的统计分析》
8.1.1变量间的相关关系
现实世界中还存在这样的情况:
两个变量之间有关系,但密切程度又达不到函数关系的程度.
如:人的体重与身高存在关系,但由一个人的身高值并不能唯一确定他的体重值.
两个变量的关系
不相关:身高与视力
相关关系
函数关系:速度(x)与路程(y)
线性相关
非线性相关
问题:该如何刻画这两个变量之间的相关关系呢?下面我们就来研究这个问题.
1.变量间的相关关系
一个人的体重与他的身高有关系.
一般而言,个子高的人往往体重值较大,个子矮的人往往体重值较小.
但身高并不是体重的唯一决定因素,例如:生活中的饮食习惯、体育锻炼、睡眠时间以及遗传因素等也是影响体重的重要因素.
两个变量有关系,但又没有确切到可由其中的一个去精确地决定另一个的程度,这种关系称为相关关系.
生活中具有相关关系的变量
【子女身高y与父亲身高x之间的关系】一般来说,父亲的个子高(矮),其子女的个子也会比较高(矮);但影响子女身高的因素,除父亲身高外还有其他因素,例如母亲身高、饮食结构、体育锻炼等,因此父亲身高又不能完全决定子女身高.
【商品销售收入y与广告支出x之间的关系】一般来说,广告支出越多,商品销售收入越高,但广告支出并不是决定商品销售收入的唯一因素,商品销售收入还与产品质量、居民收入等因素有关.
生活中具有相关关系的变量
【空气污染指数y与汽车保有量x之间的关系】一般来说,汽车保有量增加,空气污染指数会上升;但汽车保有量并不是造成空气污染的唯一因素,气象条件、工业生产排放、居民生活和取暖、垃圾焚烧等都是影响空气污染指数的因素.
【粮食亩产量y与施肥量x之间的关系】在一定范围内,施肥量越大,粮食亩产量就越高;但施肥量并不是决定粮食亩产量的唯一因素,粮食亩产量还要受到土壤质量、降水量、田间管理水平等因素的影响.
刻画变量间的相关关系
子女身高y与父亲身高x之间的关系
商品销售收入y与广告支出x之间的关系
空气污染指数y与汽车保有量x之间的关系
粮食亩产量y与施肥量x之间的关系
在相关关系中,无法直接用函数去描述变量y与变量x之间的关系。
根据以往积累的经验做出推断,“经验之中有规律”,经验的确可以为我们的决策提供一定的依据,但仅凭经经验推断又有不足,比如:不同经验的人对同一情形可能会得出不同的结论,不是所有的情形都有经验可循等.
借助数据说话,即通过样本数据分析,从数据中提取信息,并构建适当的模型,再利用模型进行估计或推断.
案例探究:刻画人体脂肪含量和年龄的相关关系
问题:在对人体的脂肪含量和年龄之间关系的研究中,科研人员获得了一些年龄和脂肪含量的简单随机样本数据,如表所示. 表中每个编号下的年龄和脂肪含量数据都是对同一个体的观测结果,它们构成了成对数据.
编号 1 2 3 4 5 6 7 8 9 10 11 12 13 14
年龄 23 27 39 41 45 49 50 53 54 56 57 58 60 61
脂肪 9.5 17.8 21.2 25.9 27.5 26.3 28.2 29.6 30.2 31.4 30.8 33.5 35.2 34.6
思考:根据以上数据,你能直观刻画并推断人体的脂肪含量与年龄之间存在怎样的关系吗?
散点图
散点图是描述成对数据之间关系的一种直观方法.
案例探究:刻画人体脂肪含量和年龄的相关关系
观察和推断:观察由人体的脂肪含量和年龄的简单随机样本数据绘制而成的散点图变化趋势,推断两个变量的相关关系.
两个变量正相关
这些散点大致落在一条从左下角到右上角的直线附近;
表明随年龄值的增加,相应的脂肪含量值呈增加趋势.
这些散点大致落在一条从左上角到右下角的直线附近;
两个变量负相关
2.变量间相关关系的类型
从整体上看,
当一个变量的值增加时,另一个变量的相应值也呈现增加的趋势,
则称两个变量正相关;
当一个变量的值增加时,另一个变量的相应值呈现减小的趋势,
则称这两个变量负相关.
如果两个变量的取值呈现正相关或负相关,而且散点落在一条直线附近,则称这两个变量线性相关.
线性相关
非线性相关
(曲线相关)
2.变量间相关关系的类型
散点杂乱无章,无规律可言,看不出两个变量有什么相关性
有相关性
观察散点图中成对样本数据的分布规律,可大致推断两个变量是否存在相关关系、是正相关还是负相关、是线性相关还是非线性相关等.
散点图虽然直观,但无法确切(量化)地反映成对样本数据的相关类型和相关程度的大小.
形
数
思考1:能否引入一个适当的“数字特征”,来度量样本数据是正相关还是负相关呢?
选修三 《第八章 成对数据的统计分析》
8.1.2样本相关系数
探究1:正相关和负相关的定量分析
设变量和经过随机抽样获得的成对样本数据为,,
其中,,,和,,,的均值分别为和.
将数据以为原点进行平移,得到平移后的成对数据为,
,,,并绘制散点图.
若变量x和y 正相关,则关于均值平移后的大多数散点将分布在第一、三象限,对应的成对数据同号的居多,即和同号
若变量x和y 负相关,则关于均值平移后的大多数散点将分布在第二、四象限,对应的成对数据异号的居多,即和异号
平移
形
数
探究2:相关程度大小的定量分析
思考2:Lxy的大小一定能度量出成对样本数据的相关程度大小吗?
是不是Lxy越大,两个变量的相关程度越强?
Lxy>0表明成对样本数据正相关;Lxy<0表明成对样本数据负相关.
Lxy的大小与数据的度量得有关,如:在研究体重与身高之间的相关程度时,如果体重的单位不变,把身高的单位由米改为厘米,则相应的Lxy将变为原来的100倍,即(Lxy)2>(Lxy)1,但单位的改变并不会导致体重与身高之间相关程度的改变.
不宜直接用Lxy度量成对样本数据相关程度的大小.
为了消除度量单位的影响,需要对数据作进一步的“标准化”处理.
形
数
Bug:Lxy的大小受数据的度量单位的影响,但单位的改变并不会导致两个变量之间相关程度的改变.
探究2:相关程度大小的定量分析
为了消除度量单位的影响,需要对数据作进一步的“标准化”处理.
称r为变量x和变量y的样本(线性)相关系数.
新知:样本(线性)相关系数r
①r的正负:反映成对样本数据的变化趋势
变量x和变量y的样本(线性)相关系数:
思考3:r的大小能否刻画成对样本数据的相关程度的强弱?r的取值范围是什么?
强
强
弱
弱
探究3:样本相关系数r的取值范围
观察r的结构,联想到二维(平面)向量、三维(空间)向量数量积的坐标表示,
我们将向量的维数推广到n维,
n维向量的数量积仍定义为:,其中θ为向量的夹角.
n维向量的数量积的坐标表示仍为:若和,
则.
新知:样本(线性)相关系数r
①r的正负:反映成对样本数据的变化趋势
变量x和变量y的样本(线性)相关系数:
②r的范围: 1≤r≤1
探究4:|r|=1时成对样本数据的关系
思考4:当|r|=1时,成对样本数据之间具有怎样的关系呢?
即此时两个变量之间满足一种线性(函数)关系,即满足完全线性相关.
故|r|越接近1时,线性相关程度越强;
|r|越接近0时,线性相关程度越弱;
若所有样本点(xi,yi)
(i=1,2,…,n)都在直线y=-2x+1上,则这组样本数据的样本相关系数为( )
①r的正负:反映成对样本数据的变化趋势
变量x和变量y的样本(线性)相关系数:
②r的范围: 1≤r≤1
③|r|的大小:反映成对样本数据线性相关的程度(即散点集中于某条直线的程度):
|r|越接近1:线性相关程度越强;
|r|越接近0:线性相关程度越弱.
r=0时,只表明成对样本数据间无线性相关关系,但不排除它们有其他相关关系.
④样本容量越大,用样本相关系数估计两个变量的相关系数的效果越好.
r=0.97
r=-0.85
r=0.24
r=-0.05
正线性相关程度很强
负线性相关程度较强
正线性相关程度很弱
负线性相关程度极弱
①r的正负:反映成对样本数据的变化特征
②r的范围: 1≤r≤1
③|r|的大小:反映成对样本数据间线性相关的程度(即散点集中于一条直线的程度):
当|r|越接近1时,线性相关程度越强;当|r|越接近0时,线性相关程度越弱.
新知:样本(线性)相关系数r
新知:样本(线性)相关系数r
如:要确切了解脂肪含量y与年龄x的线性相关程度,需要调查所有人的年龄及其脂肪含量,再将得到的成对数据代入r的公式,计算出相关系数r.
在实际中,获得总体中所有的成对数据往往是不容易的.
在有限的总体中,可以利用这两个变量取值的所有成对数据,通过上述公式就可计算出两个变量的相关系数,这个相关系数就能确切地反映变量之间相关关系的正负性及线性相关程度的强弱.
通过抽样获取两个变量的一些成对样本数据,再计算出样本相关系数,通过样本相关系数去估计总体相关系数,从而了解两个变量之间的相关程度.
思想:用样本估计总体
样本容量越大,用样本相关系数估计两个变量的相关系数的效果越好.
例题点拨
例1.根据表中脂肪含量和年龄的样本数据,推断两个变量是否线性相关,计算样本相关系数,并推断它们的相关程度.
编号 1 2 3 4 5 6 7 8 9 10 11 12 13 14
年龄 23 27 39 41 45 49 50 53 54 56 57 58 60 61
脂肪 9.5 17.8 21.2 25.9 27.5 26.3 28.2 29.6 30.2 31.4 30.8 33.5 35.2 34.6
解:先画出散点图,如图所示.
观察散点图,可看出样本点都集中在一条直线附近,由此推断脂肪含量和年龄线性相关.
代入公式可得样本相关系数r≈0.97,可以推断脂肪含量和年龄这两个变量正线性相关,且相关程度很强.
练习巩固
练习.有一个同学家开了一个小卖部,他为了研究气温对热饮料销售的影响,经过统计,得到一个卖出的热饮杯数与当天气温的数据的散点图和对比表.
解:观察散点图,可看出样本点都集中在一条直线附近,由此推断脂肪含量和年龄线性相关.
代入公式可得样本相关系数r≈﹣0.97,可以推断脂肪含量和年龄这两个变量的负线性相关程度很强.
摄氏温度x -5 4 7 10 15 23 30 36
热饮杯数y 162 128 115 135 89 71 63 37
画出散点图,并用相关系数r判断热饮杯数与当天气温的关系的强弱.
例题点拨
例3.在某校高一年级中随机抽取25名男生,测得他们的身高、体重、臂展等数据,如下表所示.体重与身高、臂展与身高分别具有怎样的相关性?
解:先画出散点图,如图所示.
从散点图看,两个散点图都呈现出线性相关.
通过计算得到体重与身高、臂展与身高的样本相关系数分别约为0.34和0.78,都为正线性相关.
r1≈0.34
∵r2>r1,∴臂展与身高的相关程度更高.
r2≈0.78
【注】在作图中,由于存在误差,有时很难判断这些点是否分布在一条直线的附近,从而就很难判断两个变量之间是否具有线性相关关系,此时就必须利用线性相关系数来判断.
例题点拨
例2.有人收集了某城市居民年收入(所有居民在一年内收入得总和)与A商品销售额的10年数据,如表所示.
画出散点图,推断成对样本数据是否线性相关,并通过样本相关系数推断居民年收入与A商品销售额的相关程度和变化趋势的异同.
解:先画出散点图,如图所示.
从散点图看,A商品销售额与居民年收入的样本数据呈现出线性相关关系.
代入公式可得样本相关系数r≈0.95,A商品销售额与居民年收入正线性相关,即A商品销售额与居民年收入有相同的变化趋势,且相关程度很强.
实际理解与运用
P104-3.根据物理中的胡克定律,弹簧伸长的长度与所受的外力成正比.
测得一根弹簧伸长长度x和相应所受外力F的一组数据如下:
两个变量的样本相关系数是否为1 若不是,请你解释其中的原因.
析:计算可得r≈0.9997
由此可得,弹簧伸长长度x和相应所受外力F几乎完全正线性相关,
样本数据没有完全正线性相关,跟测量存在误差、弹簧制造工艺等因素有关.
实际理解与运用
P104-4.某地区的环境条件适合天鹅栖息繁衍.有人发现了一个有趣的现象:该地区有5个村庄,其中3个村庄附近栖息的天鹅较多,婴儿出生率也较高;2个村庄附近栖息的天鹅较少,婴儿的出生率也较低.
有人认为婴儿出生率和天鹅数之间存在相关关系,并得出一个
结论:天鹅能够带来孩子. 你同意这个结论吗 为什么
从5对统计数据看,婴儿出生率和天鹅数正相关.
但样本数据较少,得出上述结论的可靠性不高。
天鹅数多的地方,婴儿出生率也高,可能是受其他因素的影响,如 :某个村庄生态环境好,适合人类居住,有利于婴儿出生,也适合天鹅栖息繁衍,∴天鹅数多不是婴儿出生率高的原因。
函数关系是一种因果关系;
相关关系不一定是因果关系,也可能是伴随关系.
END
