5.3简单的轴对称图形第3课时 课件(共17张PPT)2023-2024学年北师大版数学七年级下册
文档属性
| 名称 | 5.3简单的轴对称图形第3课时 课件(共17张PPT)2023-2024学年北师大版数学七年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-17 11:31:02 | ||
图片预览





文档简介
(共17张PPT)
5.3 简单的轴对称图形
第3课时
配套北师大版
学习目标
准备好了吗?一起去探索吧!
简单的轴对称图形
1.运用作图和实验的方法,探索角平分线的有关性质.
2.能运用角平分线的性质解决实际问题.
3.会用尺规作出已知角的平分线,能规范地写出已知、求作和作法.
4.利用折纸的方法探索角的对称性,进一步体验轴对称的特征,发展空间观念.
重点
难点
如果一个平面图形沿一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形,这条直线叫做对称轴.
问题2:角是轴对称图形吗?如何验证你的结论?
问题1:什么是轴对称图形?
角是轴对称图形.
可以作出一个角对折一下看看角的两边是否重合.
复习回顾
请拿出你作的∠AOB,不利用工具,将它分成两个相等的角.你有什么办法?
情境引入
A
O
B
C
打开纸片,看看折痕与这个角有何关系?
结论:角是轴对称图形,对称轴是角平分线所在的直线.
对折
折痕平分了∠AOB
(1)在一张纸上任意画出∠AOB,沿角的两边将角剪下,将这个角的两边重合,折痕就是∠AOB的平分线.
(2)在∠AOB的角平分线上任意取一点C,分别折出过点C且与∠AOB的两边垂直的直线,垂足分别为D、E.将∠AOB再次对折,折痕CD与CE能重合吗?
(3)改变点C的位置,CD和CE还相等吗?
做一做
A
O
B
C
D
E
重合
相等
C
D
E
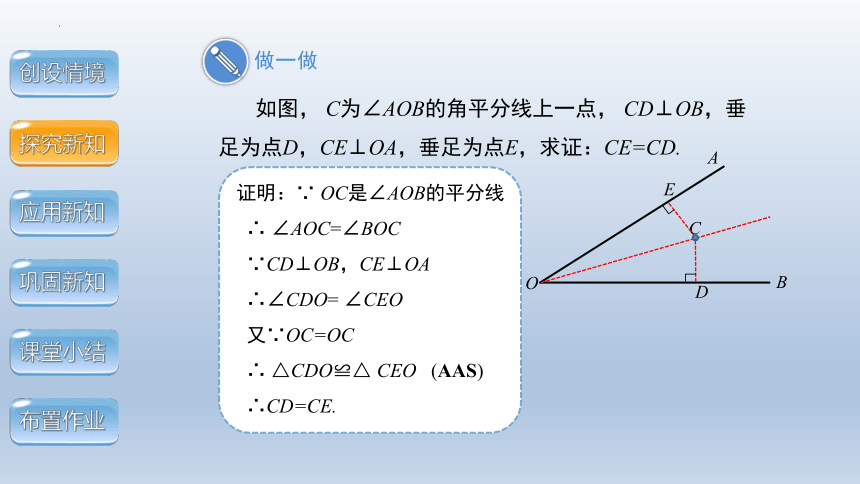
如图, C为∠AOB的角平分线上一点, CD⊥OB,垂足为点D,CE⊥OA,垂足为点E,求证:CE=CD.
做一做
A
O
B
C
D
E
证明:∵ OC是∠AOB的平分线
∴ ∠AOC=∠BOC
∵CD⊥OB,CE⊥OA
∴∠CDO= ∠CEO
又∵OC=OC
∴ △CDO≌△ CEO (AAS)
∴CD=CE.
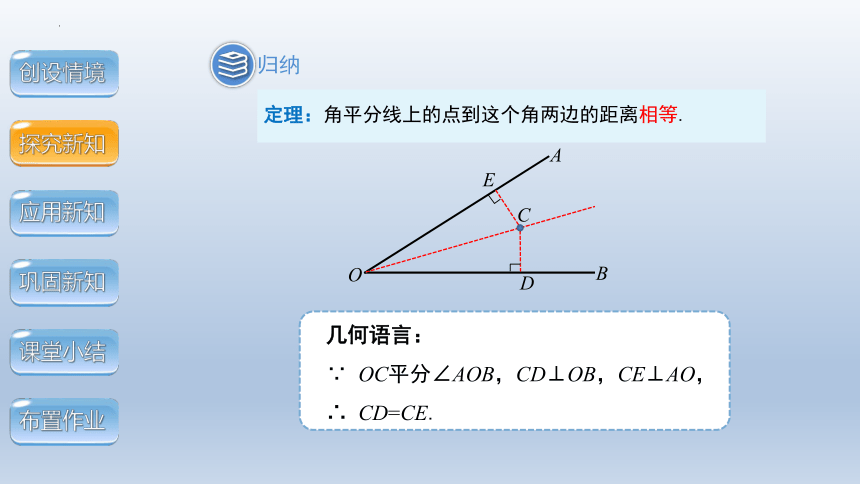
定理:角平分线上的点到这个角两边的距离相等.
归纳
几何语言:
∵ OC平分∠AOB,CD⊥OB,CE⊥AO,∴ CD=CE.
A
B
C
D
O
E
典型例题
例 利用尺规,作∠AOB(如右图)的平分线.
已知:∠AOB,如右图.
求作:射线OC,使∠AOC=∠BOC.
①利用构造全等三角形的方法,先在∠AOB的两边OA和OB上截取相等的线段OD、OE分别作为两个三角形的两边.
②在∠AOB内找到点C,使CD=CE.
B
A
O
③则△COD≌△COE (SSS),得到∠AOC=∠BOC.
典型例题
例 利用尺规,作∠AOB(如右图)的平分线.
已知:∠AOB,如右图.
求作:射线OC,使∠AOC=∠BOC.
B
A
O
E
D
C
作法:
1.以点O为圆心,适当长为半径作弧,交OA于D,交OB于E,则OD=OE.
3.作射线OC.
2.分别以D,E为圆心.大于 的长度为半径作弧.两弧在∠AOB内交于点C.
OC就是∠AOB的平分线.
想一想
如图,在Rt△ABC中,∠C=90°,BD是∠ABC的平分线,DE⊥AB,垂足为点E.DE与DC相等吗?为什么?
∟
∟
E
A
B
D
C
①由BD是∠ABC的平分线想到可以应用角平分线定理.
②DC⊥BC,DE⊥AB,满足角平分线定理的两个条件.
③应用角平分线定理可得DE=DC.
想一想
如图,在Rt△ABC中,∠C=90°,BD是∠ABC的平分线,DE⊥AB,垂足为点E.DE与DC相等吗?为什么?
证明: ∵BD是∠ABC的平分线
在Rt△ABC中,∠C=90°
∴DC⊥BC
又∵DE⊥AB
∴ DE=DC.
相等,可以由角平分线定理证明.
∟
∟
E
A
B
D
C
随堂练习
1.如图,OP平分∠MON,PA⊥ON,垂足为点A,点Q是射线OM上的一个动点.若PA=2,则线段PQ长度的最小值为多少?请说明理由.
∟
M
P
O
A
N
Q
解:长度最小值为2.
∵直线外一点与直线上各点的连线中,垂线段最短.
∴过P做PQ⊥OM,垂足为Q,此时PQ即为所求.
又∵OP平分∠MON,PA⊥ON.
∴PQ=PA=2.
∟
随堂练习
2.如图所示,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB,并交 BC于点D,DE⊥AB于点E,若 AB=6cm,则△DEB的周长是多少
∟
C
D
E
A
B
∟
解:∵∠C=90°∴AC⊥DC
又∵AD平分∠CAB,DE⊥AB
∴DE=DC,△ACD≌△AED (AAS)
∴AC=AE
又∵AC=BC,∴BC=AE
∴△DEB的周长=EB+BD+DE=EB+BD+DC
=EB+BC=EB+AE=AB=6cm.
解:∵AD是△ABC中∠BAC的平分线
又∵DE⊥AB,DF⊥AC
∴DF=DE=2,
S△ABC=S△ABD+S△ADC
= AB·DE+ AC·DF
∴
解得AC=3.
随堂练习
3.如图所示,AD是△ABC中∠BAC的平分线,DE⊥AB于点E,DF⊥AC于点F.S△ABC=7,DE=2,AB=4,则AC的长是多少?
A
B
D
E
F
C
∟
∟
角平分线定理:
简单的轴对称图形
角的对称性:
角平分线上的点到这个角两边的距离相等.
角是轴对称图形,角平分线所在的直线是它的对称轴.
注意:使用时,角平分和垂直于角的两边两个条件缺一不可.
作已知角的平分线:
利用尺规,构造全等三角形.
教科书 第126页
习题5.5 第2、3题
再见
5.3 简单的轴对称图形
第3课时
配套北师大版
学习目标
准备好了吗?一起去探索吧!
简单的轴对称图形
1.运用作图和实验的方法,探索角平分线的有关性质.
2.能运用角平分线的性质解决实际问题.
3.会用尺规作出已知角的平分线,能规范地写出已知、求作和作法.
4.利用折纸的方法探索角的对称性,进一步体验轴对称的特征,发展空间观念.
重点
难点
如果一个平面图形沿一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形,这条直线叫做对称轴.
问题2:角是轴对称图形吗?如何验证你的结论?
问题1:什么是轴对称图形?
角是轴对称图形.
可以作出一个角对折一下看看角的两边是否重合.
复习回顾
请拿出你作的∠AOB,不利用工具,将它分成两个相等的角.你有什么办法?
情境引入
A
O
B
C
打开纸片,看看折痕与这个角有何关系?
结论:角是轴对称图形,对称轴是角平分线所在的直线.
对折
折痕平分了∠AOB
(1)在一张纸上任意画出∠AOB,沿角的两边将角剪下,将这个角的两边重合,折痕就是∠AOB的平分线.
(2)在∠AOB的角平分线上任意取一点C,分别折出过点C且与∠AOB的两边垂直的直线,垂足分别为D、E.将∠AOB再次对折,折痕CD与CE能重合吗?
(3)改变点C的位置,CD和CE还相等吗?
做一做
A
O
B
C
D
E
重合
相等
C
D
E
如图, C为∠AOB的角平分线上一点, CD⊥OB,垂足为点D,CE⊥OA,垂足为点E,求证:CE=CD.
做一做
A
O
B
C
D
E
证明:∵ OC是∠AOB的平分线
∴ ∠AOC=∠BOC
∵CD⊥OB,CE⊥OA
∴∠CDO= ∠CEO
又∵OC=OC
∴ △CDO≌△ CEO (AAS)
∴CD=CE.
定理:角平分线上的点到这个角两边的距离相等.
归纳
几何语言:
∵ OC平分∠AOB,CD⊥OB,CE⊥AO,∴ CD=CE.
A
B
C
D
O
E
典型例题
例 利用尺规,作∠AOB(如右图)的平分线.
已知:∠AOB,如右图.
求作:射线OC,使∠AOC=∠BOC.
①利用构造全等三角形的方法,先在∠AOB的两边OA和OB上截取相等的线段OD、OE分别作为两个三角形的两边.
②在∠AOB内找到点C,使CD=CE.
B
A
O
③则△COD≌△COE (SSS),得到∠AOC=∠BOC.
典型例题
例 利用尺规,作∠AOB(如右图)的平分线.
已知:∠AOB,如右图.
求作:射线OC,使∠AOC=∠BOC.
B
A
O
E
D
C
作法:
1.以点O为圆心,适当长为半径作弧,交OA于D,交OB于E,则OD=OE.
3.作射线OC.
2.分别以D,E为圆心.大于 的长度为半径作弧.两弧在∠AOB内交于点C.
OC就是∠AOB的平分线.
想一想
如图,在Rt△ABC中,∠C=90°,BD是∠ABC的平分线,DE⊥AB,垂足为点E.DE与DC相等吗?为什么?
∟
∟
E
A
B
D
C
①由BD是∠ABC的平分线想到可以应用角平分线定理.
②DC⊥BC,DE⊥AB,满足角平分线定理的两个条件.
③应用角平分线定理可得DE=DC.
想一想
如图,在Rt△ABC中,∠C=90°,BD是∠ABC的平分线,DE⊥AB,垂足为点E.DE与DC相等吗?为什么?
证明: ∵BD是∠ABC的平分线
在Rt△ABC中,∠C=90°
∴DC⊥BC
又∵DE⊥AB
∴ DE=DC.
相等,可以由角平分线定理证明.
∟
∟
E
A
B
D
C
随堂练习
1.如图,OP平分∠MON,PA⊥ON,垂足为点A,点Q是射线OM上的一个动点.若PA=2,则线段PQ长度的最小值为多少?请说明理由.
∟
M
P
O
A
N
Q
解:长度最小值为2.
∵直线外一点与直线上各点的连线中,垂线段最短.
∴过P做PQ⊥OM,垂足为Q,此时PQ即为所求.
又∵OP平分∠MON,PA⊥ON.
∴PQ=PA=2.
∟
随堂练习
2.如图所示,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB,并交 BC于点D,DE⊥AB于点E,若 AB=6cm,则△DEB的周长是多少
∟
C
D
E
A
B
∟
解:∵∠C=90°∴AC⊥DC
又∵AD平分∠CAB,DE⊥AB
∴DE=DC,△ACD≌△AED (AAS)
∴AC=AE
又∵AC=BC,∴BC=AE
∴△DEB的周长=EB+BD+DE=EB+BD+DC
=EB+BC=EB+AE=AB=6cm.
解:∵AD是△ABC中∠BAC的平分线
又∵DE⊥AB,DF⊥AC
∴DF=DE=2,
S△ABC=S△ABD+S△ADC
= AB·DE+ AC·DF
∴
解得AC=3.
随堂练习
3.如图所示,AD是△ABC中∠BAC的平分线,DE⊥AB于点E,DF⊥AC于点F.S△ABC=7,DE=2,AB=4,则AC的长是多少?
A
B
D
E
F
C
∟
∟
角平分线定理:
简单的轴对称图形
角的对称性:
角平分线上的点到这个角两边的距离相等.
角是轴对称图形,角平分线所在的直线是它的对称轴.
注意:使用时,角平分和垂直于角的两边两个条件缺一不可.
作已知角的平分线:
利用尺规,构造全等三角形.
教科书 第126页
习题5.5 第2、3题
再见
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
