四川省广元市2014-2015学年人教版数学选修1-1:2.1.1《椭圆及其标准方程》课件
文档属性
| 名称 | 四川省广元市2014-2015学年人教版数学选修1-1:2.1.1《椭圆及其标准方程》课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 572.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-06-21 14:37:12 | ||
图片预览







文档简介
课件20张PPT。2.1《椭圆》 教学目标 1.知识目标
①建立直角坐标系,根据椭圆的定义建立椭圆的标准方程,
②能根据已知条件求椭圆的标准方程,
③进一步感受曲线方程的概念,了解建立曲线方程的基本方法,体会数形结合的数学思想。
2.能力目标
①让学生感知数学知识与实际生活的密切联系,培养解决实际问题的能力,
②培养学生的观察能力、归纳能力、探索发现能力,
③提高运用坐标法解决几何问题的能力及运算能力。3.情感目标
①亲身经历椭圆标准方程的获得过程,感受数学美的熏陶,
②通过主动探索,合作交流,感受探索的乐趣和成功的体验,体会数学的理性和严谨,
③养成实事求是的科学态度和契而不舍的钻研精神,形成学习数学知识的积极态度。
4、重点难点
基于以上分析,我将本课的教学重点、难点确定为:
①重点:感受建立曲线方程的基本过程,掌握椭圆的标准方程及其推导方法,
②难点:椭圆的标准方程的推导。
§2.1 椭圆及其标准方程
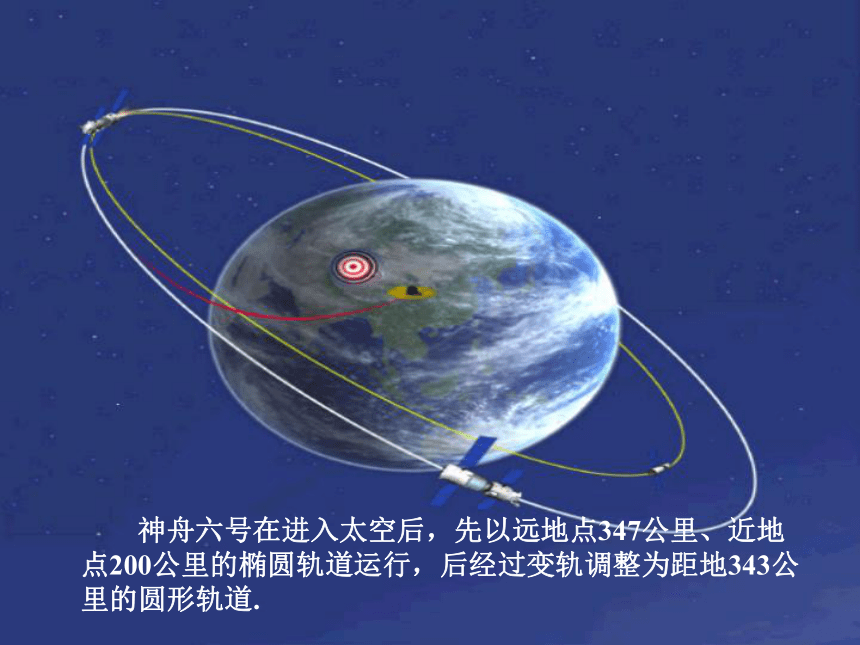
2003年10月15日9时我国首位航天员杨利伟乘坐的“神舟”五号载人飞船,在酒泉卫星发射中心成功升空。随着那一声冲天而起的火光和共鸣,它顺利地进入了预定轨道。它升起的不仅是载人飞船,还有中国人的骄傲与自信! 设置情境 问题诱导 2005年10月12日上午9时,“神舟六号”载人飞船顺利升空,实现多人多天飞行,标志着我国航天事业又上了一个新台阶,请问: “神舟六号”载人飞船的运行轨道是什么? 神舟六号在进入太空后,先以远地点347公里、近地点200公里的椭圆轨道运行,后经过变轨调整为距地343公里的圆形轨道.复习提问:
1.圆的定义是什么?
2.圆的标准方程是什么?绘图纸上的三个问题1.视笔尖为动点,两个图钉为定点,动点到两定点距离之和符合什么条件?其轨迹如何?
2.改变两图钉之间的距离,使其与绳长相等,画出的图形还是椭圆吗?
3.绳长能小于两图钉之间的距离吗? 导入新课: 探究:|MF1|+ |MF2|>|F1F2| 椭圆|MF1|+ |MF2|=|F1F2| 线段|MF1|+ |MF2|<|F1F2| 不存在xy 以F1、F2 所在直线为 x 轴,线段 F1F2
的垂直平分线为 y 轴建立直角坐标系.P( x , y )设 P( x,y )是椭圆上任意一点设F1F=2c,则有F1(-c,0)、F2(c,0) 椭圆上的点满足PF1+PF2
为定值,设为2a,则2a>2c则:即:Ob2x2+a2y2=a2b2 探究:如何建立椭圆的方程?方
程
特
点(2)在椭圆两种标准方程中,总有a>b>0;(4)a、b、c都有特定的意义,
a—椭圆上任意一点P到F1、F2距离和的一半;c—半焦距.
有关系式 成立。2.椭圆的标准方程(3)焦点在大分母变量所对应的那个轴上;(1)方程的左边是两项平方和的形式,等号的右边是1;变式演练 加深理解 解:(1)所求椭圆标准方程为 (2)所求椭圆标准方程为 例2 求适合下列条件的椭圆的标准方程. (1)焦点在x轴上,且经过点(2,0)和点(0,1). (2)焦点在y轴上,与y轴的一个交点为P(0,-10),P到它较近的一个焦点的距离等于2.解:(1)所求椭圆的标准方程为(2)所求椭圆的标准方程是.求椭圆标准方程的解题步骤:(1)确定焦点的位置;(2)设出椭圆的标准方程;(3)用待定系数法确定a、b的值,
写出椭圆的标准方程.例3 已知椭圆经过两点 ,求椭圆的标准方程 解:设椭圆的标准方程则有 ,解得 所以,所求椭圆的标准方程为变式题组一变式题组二反思总结 提高素质 椭圆标准方程的求法:一定焦点位置;
二设椭圆方程;
三求a、b的值.F1(-c,0)、F2(c,0)F1(0,-c)、F2(0,c) 平面内与两定点F1、F2的距离的和等于常数(大于|F1F2|)的点的轨迹叫做椭圆.b2 = a2 –c2 椭圆的两种标准方程中,总是 a>b>0. 所以哪个项的分母大,焦点就在那个轴上;反过来,焦点在哪个轴上,相应的那个项的分母就越大.作业:
一. 人教版选修P42 1,2再见
①建立直角坐标系,根据椭圆的定义建立椭圆的标准方程,
②能根据已知条件求椭圆的标准方程,
③进一步感受曲线方程的概念,了解建立曲线方程的基本方法,体会数形结合的数学思想。
2.能力目标
①让学生感知数学知识与实际生活的密切联系,培养解决实际问题的能力,
②培养学生的观察能力、归纳能力、探索发现能力,
③提高运用坐标法解决几何问题的能力及运算能力。3.情感目标
①亲身经历椭圆标准方程的获得过程,感受数学美的熏陶,
②通过主动探索,合作交流,感受探索的乐趣和成功的体验,体会数学的理性和严谨,
③养成实事求是的科学态度和契而不舍的钻研精神,形成学习数学知识的积极态度。
4、重点难点
基于以上分析,我将本课的教学重点、难点确定为:
①重点:感受建立曲线方程的基本过程,掌握椭圆的标准方程及其推导方法,
②难点:椭圆的标准方程的推导。
§2.1 椭圆及其标准方程
2003年10月15日9时我国首位航天员杨利伟乘坐的“神舟”五号载人飞船,在酒泉卫星发射中心成功升空。随着那一声冲天而起的火光和共鸣,它顺利地进入了预定轨道。它升起的不仅是载人飞船,还有中国人的骄傲与自信! 设置情境 问题诱导 2005年10月12日上午9时,“神舟六号”载人飞船顺利升空,实现多人多天飞行,标志着我国航天事业又上了一个新台阶,请问: “神舟六号”载人飞船的运行轨道是什么? 神舟六号在进入太空后,先以远地点347公里、近地点200公里的椭圆轨道运行,后经过变轨调整为距地343公里的圆形轨道.复习提问:
1.圆的定义是什么?
2.圆的标准方程是什么?绘图纸上的三个问题1.视笔尖为动点,两个图钉为定点,动点到两定点距离之和符合什么条件?其轨迹如何?
2.改变两图钉之间的距离,使其与绳长相等,画出的图形还是椭圆吗?
3.绳长能小于两图钉之间的距离吗? 导入新课: 探究:|MF1|+ |MF2|>|F1F2| 椭圆|MF1|+ |MF2|=|F1F2| 线段|MF1|+ |MF2|<|F1F2| 不存在xy 以F1、F2 所在直线为 x 轴,线段 F1F2
的垂直平分线为 y 轴建立直角坐标系.P( x , y )设 P( x,y )是椭圆上任意一点设F1F=2c,则有F1(-c,0)、F2(c,0) 椭圆上的点满足PF1+PF2
为定值,设为2a,则2a>2c则:即:Ob2x2+a2y2=a2b2 探究:如何建立椭圆的方程?方
程
特
点(2)在椭圆两种标准方程中,总有a>b>0;(4)a、b、c都有特定的意义,
a—椭圆上任意一点P到F1、F2距离和的一半;c—半焦距.
有关系式 成立。2.椭圆的标准方程(3)焦点在大分母变量所对应的那个轴上;(1)方程的左边是两项平方和的形式,等号的右边是1;变式演练 加深理解 解:(1)所求椭圆标准方程为 (2)所求椭圆标准方程为 例2 求适合下列条件的椭圆的标准方程. (1)焦点在x轴上,且经过点(2,0)和点(0,1). (2)焦点在y轴上,与y轴的一个交点为P(0,-10),P到它较近的一个焦点的距离等于2.解:(1)所求椭圆的标准方程为(2)所求椭圆的标准方程是.求椭圆标准方程的解题步骤:(1)确定焦点的位置;(2)设出椭圆的标准方程;(3)用待定系数法确定a、b的值,
写出椭圆的标准方程.例3 已知椭圆经过两点 ,求椭圆的标准方程 解:设椭圆的标准方程则有 ,解得 所以,所求椭圆的标准方程为变式题组一变式题组二反思总结 提高素质 椭圆标准方程的求法:一定焦点位置;
二设椭圆方程;
三求a、b的值.F1(-c,0)、F2(c,0)F1(0,-c)、F2(0,c) 平面内与两定点F1、F2的距离的和等于常数(大于|F1F2|)的点的轨迹叫做椭圆.b2 = a2 –c2 椭圆的两种标准方程中,总是 a>b>0. 所以哪个项的分母大,焦点就在那个轴上;反过来,焦点在哪个轴上,相应的那个项的分母就越大.作业:
一. 人教版选修P42 1,2再见
