四川省广元市2014-2015学年人教版数学选修1-1:2.2.2《双曲线的简单几何性质》课件
文档属性
| 名称 | 四川省广元市2014-2015学年人教版数学选修1-1:2.2.2《双曲线的简单几何性质》课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 112.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-06-21 00:00:00 | ||
图片预览





文档简介
课件18张PPT。2.2.2《双曲线的简单几何性质》教学目标 知识与技能目标
了解平面解析几何研究的主要问题:(1)根据条件,求出表示曲线的方程;(2)通过方程,研究曲线的性质.理解双曲线的范围、对称性及对称轴,对称中心、离心率、顶点、渐近线的概念;掌握双曲线的标准方程、会用双曲线的定义解决实际问题;通过例题和探究了解双曲线的第二定义,准线及焦半径的概念,利用信息技术进一步见识圆锥曲线的统一定义.过程与方法目标
(1)复习与引入过程
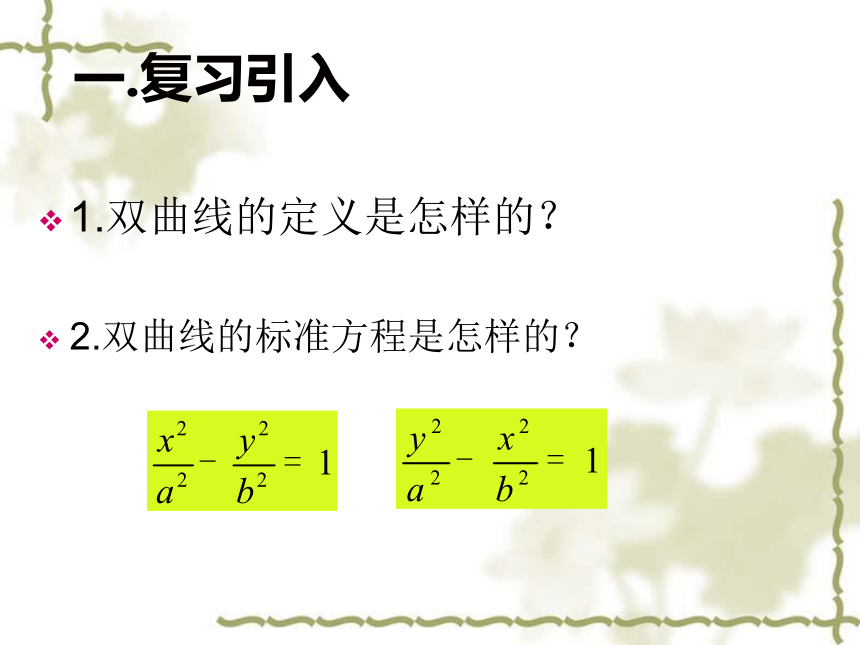
引导学生复习得到椭圆的简单的几何性质的方法,在本节课中不仅要注意通过对双曲线的标准方程的讨论,研究双曲线的几何性质的理解和应用,而且还注意对这种研究方法的进一步地培养.①由双曲线的标准方程和非负实数的概念能得到双曲线的范围;②由方程的性质得到双曲线的对称性;③由圆锥曲线顶点的统一定义,容易得出双曲线的顶点的坐标及实轴、虚轴的概念;④应用信息技术的《几何画板》探究双曲线的渐近线问题;⑤探究双曲线的扁平程度量椭圆的离心率 一.复习引入 1.双曲线的定义是怎样的?
2.双曲线的标准方程是怎样的? 双曲线的简单几何性质思考回顾
椭圆的简单几何性质 ?
①范围; ②对称性; ③顶点;
④离心率等 双曲线是否具有类似的性质呢?
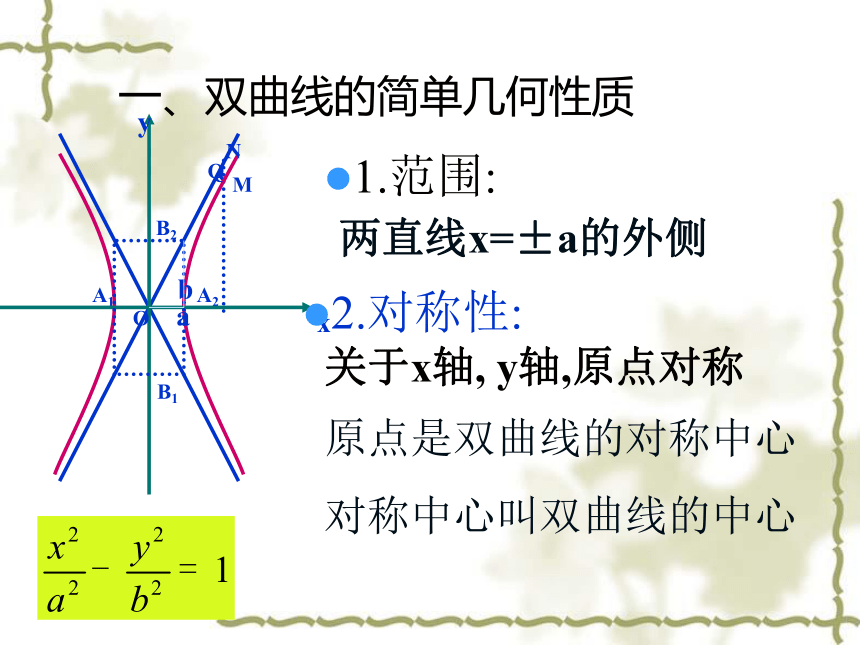
回想:我们是怎样研究上述性质的?一、双曲线的简单几何性质 1.范围:两直线x=±a的外侧2.对称性: 关于x轴, y轴,原点对称 原点是双曲线的对称中心
对称中心叫双曲线的中心一.双曲线的简单几何性质
3.顶点::(1)双曲线与x轴的两个交A (-a,0), A (a,0)叫双曲线的顶点12(2)实轴:线段A A 实轴长:2a
虚轴:线段B B 虚轴长:2b 1 2 1 2
4.渐进线: (1)渐进线的确定:矩形的对角线 (2)直线的方程: y=±-xb
a渐渐接近但永不相交(1)概念:焦距与实轴长之比5.离心率(2)定义式: e=- c a(3)范围: e>1 (c>a)(4)双曲线的形状与e的关系即:e越大,渐进线斜率越大,其开口越阔.
关于X轴、Y轴、原点都对称。
图形方程范围对称性顶点离心率准线一.双曲线的简单几何性质
1.范围: 2.对称性:3.顶点: 实轴,虚轴4.渐进线: (1)渐进线的确定:对角线 (2)直线的方程: y=±-xb
a(1)概念:5.离心率:(2)定义式: e=- c a(3)范围: e>1 (4)双曲线的形状与e的关系即:e越大,渐进线斜率越大,其开口越阔.
二. 应 用 举 例: 例1.求双曲线9y – 16x =144的实半轴与虚半轴长,焦点坐标,离心率及渐进线方程.22
例2.求一渐进线为3x+4y=0,一个焦点为(5,0)的双曲线的标准方程. 例3:点M(x,y)到定点F(5,0)的距离和它到定直线l:x=16/5的距离的比是常数5/4,求点M的轨迹。例4:双曲线型冷却塔的外形,是双曲线的一部分绕其虚轴旋转所成的曲面,它的最小半径为12m,上口半径为13m,下口半径m,高为55m,试选择适当的坐标系,求出此双曲线的方程。四.小结:1.双曲线的几何性质: ①范围; ②对称性; ③顶点; ④渐进线; ⑤离心率2.几何性质的应用再见
了解平面解析几何研究的主要问题:(1)根据条件,求出表示曲线的方程;(2)通过方程,研究曲线的性质.理解双曲线的范围、对称性及对称轴,对称中心、离心率、顶点、渐近线的概念;掌握双曲线的标准方程、会用双曲线的定义解决实际问题;通过例题和探究了解双曲线的第二定义,准线及焦半径的概念,利用信息技术进一步见识圆锥曲线的统一定义.过程与方法目标
(1)复习与引入过程
引导学生复习得到椭圆的简单的几何性质的方法,在本节课中不仅要注意通过对双曲线的标准方程的讨论,研究双曲线的几何性质的理解和应用,而且还注意对这种研究方法的进一步地培养.①由双曲线的标准方程和非负实数的概念能得到双曲线的范围;②由方程的性质得到双曲线的对称性;③由圆锥曲线顶点的统一定义,容易得出双曲线的顶点的坐标及实轴、虚轴的概念;④应用信息技术的《几何画板》探究双曲线的渐近线问题;⑤探究双曲线的扁平程度量椭圆的离心率 一.复习引入 1.双曲线的定义是怎样的?
2.双曲线的标准方程是怎样的? 双曲线的简单几何性质思考回顾
椭圆的简单几何性质 ?
①范围; ②对称性; ③顶点;
④离心率等 双曲线是否具有类似的性质呢?
回想:我们是怎样研究上述性质的?一、双曲线的简单几何性质 1.范围:两直线x=±a的外侧2.对称性: 关于x轴, y轴,原点对称 原点是双曲线的对称中心
对称中心叫双曲线的中心一.双曲线的简单几何性质
3.顶点::(1)双曲线与x轴的两个交A (-a,0), A (a,0)叫双曲线的顶点12(2)实轴:线段A A 实轴长:2a
虚轴:线段B B 虚轴长:2b 1 2 1 2
4.渐进线: (1)渐进线的确定:矩形的对角线 (2)直线的方程: y=±-xb
a渐渐接近但永不相交(1)概念:焦距与实轴长之比5.离心率(2)定义式: e=- c a(3)范围: e>1 (c>a)(4)双曲线的形状与e的关系即:e越大,渐进线斜率越大,其开口越阔.
关于X轴、Y轴、原点都对称。
图形方程范围对称性顶点离心率准线一.双曲线的简单几何性质
1.范围: 2.对称性:3.顶点: 实轴,虚轴4.渐进线: (1)渐进线的确定:对角线 (2)直线的方程: y=±-xb
a(1)概念:5.离心率:(2)定义式: e=- c a(3)范围: e>1 (4)双曲线的形状与e的关系即:e越大,渐进线斜率越大,其开口越阔.
二. 应 用 举 例: 例1.求双曲线9y – 16x =144的实半轴与虚半轴长,焦点坐标,离心率及渐进线方程.22
例2.求一渐进线为3x+4y=0,一个焦点为(5,0)的双曲线的标准方程. 例3:点M(x,y)到定点F(5,0)的距离和它到定直线l:x=16/5的距离的比是常数5/4,求点M的轨迹。例4:双曲线型冷却塔的外形,是双曲线的一部分绕其虚轴旋转所成的曲面,它的最小半径为12m,上口半径为13m,下口半径m,高为55m,试选择适当的坐标系,求出此双曲线的方程。四.小结:1.双曲线的几何性质: ①范围; ②对称性; ③顶点; ④渐进线; ⑤离心率2.几何性质的应用再见
