四川省广元市2014-2015学年人教版数学选修1-1:2.4《圆锥曲线与方程全章小结》课件
文档属性
| 名称 | 四川省广元市2014-2015学年人教版数学选修1-1:2.4《圆锥曲线与方程全章小结》课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 422.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-06-21 00:00:00 | ||
图片预览




文档简介
课件16张PPT。2.4《圆锥曲线
与方程全章小结》复习目标(1) 求长轴与短轴之和为20,焦距为 的椭圆的标准方程_________________和
(2)求与双曲线 有共同渐近线,且过点(-3, )的双曲线方程;
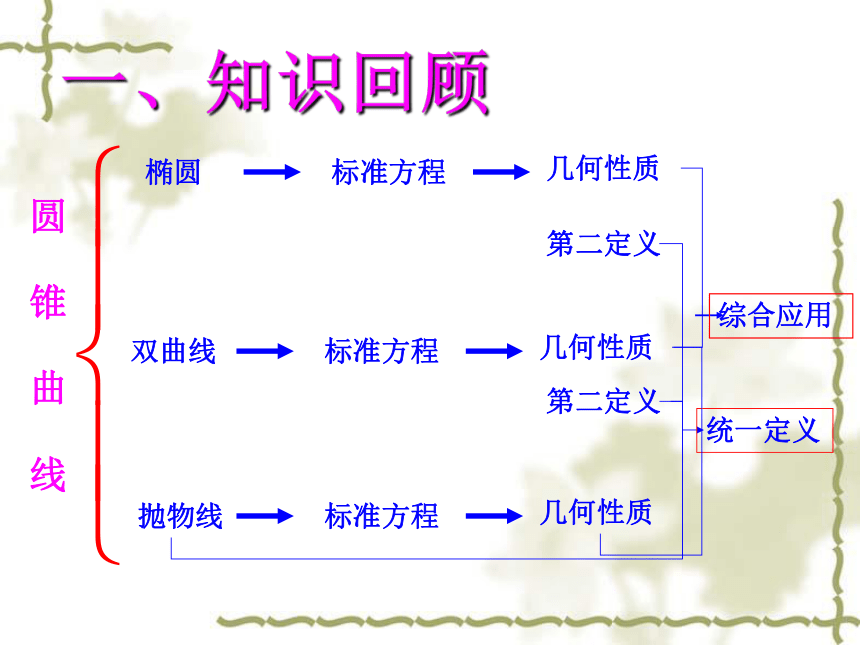
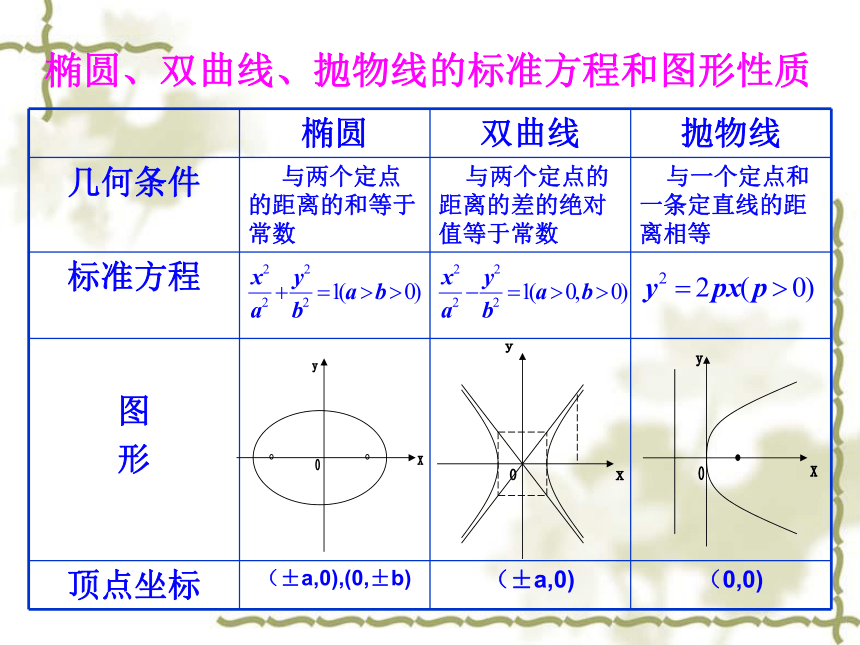
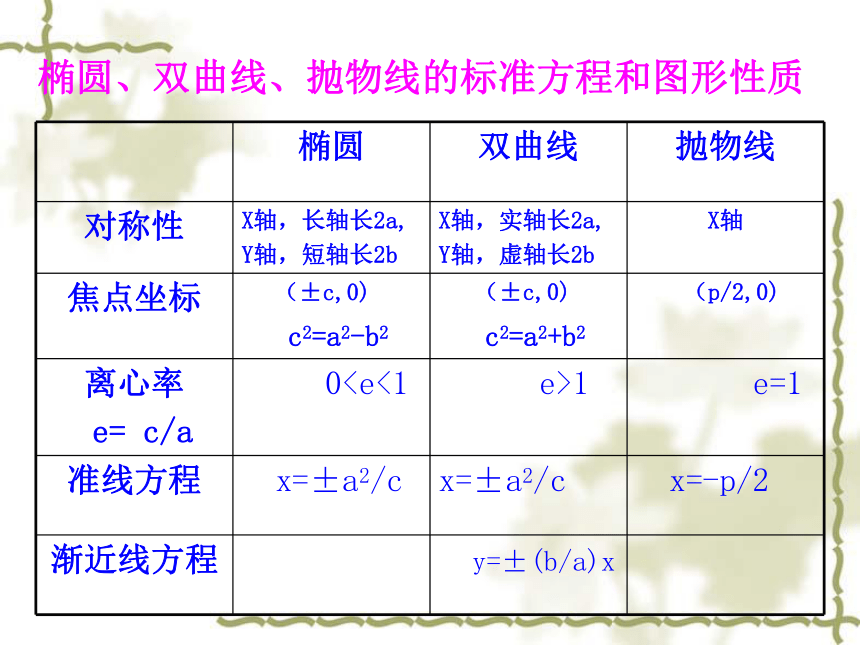
(3)一动圆M和直线l:x=-2相切,并且经过点F(2,0),则圆心M的轨迹方程是 .课前热身一、知识回顾 圆 锥 曲 线椭圆双曲线抛物线标准方程几何性质标准方程几何性质标准方程几何性质第二定义第二定义统一定义综合应用椭圆、双曲线、抛物线的标准方程和图形性质椭圆、双曲线、抛物线的标准方程和图形性质例1.求双曲线9y – 16x =144的实半轴与虚半轴长,焦点坐标,离心率及渐进线方程.22
故 渐进线方程为:y=±-x
解:把方程化成标准方程: -- -=1 y
16 x
2522故 实半轴长a=4,虚半轴长b=3∴ c=√16+9 =5.________∴ e=-5
43
4二、应用举例 例2.直线y=x-2与抛物线y2=2x相交于A、B 求证:OA⊥OB。 证法1:将y=x-2代入y2=2x中,得 (x-2)2=2x化简得 x2-6x+4=0解得:则: ∴OA⊥OB证法2:同证法1得方程 x2-6x+4=0由一元二次方程根与系数的关系,可知 x1+x2=6, x1·x2=4 ∴OA⊥OB∵y1=x1-2 , y2=x2-2;∴y1·y2=(x1-2)(x2-2)=x1·x2-2(x1+x2)+4
=4-12+4=-4 例3.一圆与圆x2+y2+6x+5=0外切,同时与圆x2+y2-6x-91=0内切,求动圆圆心的轨迹方程,并说明它是什么样的曲线解法1:如图:设动圆圆心为P(x,y),半径为R,两已知圆圆心为O1、O2。分别将两已知圆的方程
x2+y2+6x+5=0 x2+y2-6x-91=0
配方,得 (x+3)2+y2=4 (x-3)2+y2=100当⊙P与⊙O1: (x+3)2+y2=4外切时,有 |O1P|=R+2 ①
当⊙P与⊙O2: (x-3)2+y2=100内切时,有 |O2P|=10-R ②①、②式两边分别相加,得 |O1P|+|O2P|=12即化简并整理,得 3x2+4y2-108=0即可得所以,动圆圆心的轨迹是椭圆,它的长轴、短轴分别为解法2:同解法1得方程即,动圆圆心P(x,y)到点O1(-3,0)和点O2(3,0)距离的和是常数12,所以点P的轨迹是焦点为(-3,0)、(3,0),长轴长等于12的椭圆。于是可求出它的标准方程。∵2c=6 ,2a=12 , ∴ c=3 , a=6 ∴b2=36-9=27于是得动圆圆心的轨迹方程为这个动圆圆心的轨迹是椭圆,它的长轴、短轴分别为三、课堂练习 1. 动点P 到直线 x+4=0 的距离减去它到点M(2,0)的距离之差等于2,则点P 的轨迹是 ( )
A.直线 B.椭圆 C.双曲线 D.抛物线D2.P是双曲线 x2/4-y2=1 上任意一点,O为原点,则OP线段中点Q的轨迹方程是( ) 3.和圆x2+y2=1外切,且和x轴相切的动圆圆心O的轨迹方程是 。 x2=2|y|+1B做练习 3.过点P( 0 , 4 )与抛物线y2=2x只有一个公共点的直线有 条。4、直线 y=kx+1与焦点在x轴上的椭圆 x2/5+y2/m=1 总有公共点,则m的取值范围是 。 5、过点M(-2,0)的直线l与椭圆 x2+2y2=2 交于P1、P2两点,线段P1P2的中点为P,设直线 l 的斜率为k1(k1≠0),直线OP的斜率为k2,则 k1k2 的值为 ( ) 3[1,5) 已知椭圆 中,F1、F2 分
别为其 左、右焦点和点A ,试在椭圆上找一点 P,使
(1) 取得最小值;
(2) 取得最小值.AF1F2xyoPP思考题 四、小结:
1、本节课的重点是掌握圆锥曲线的定义及性质在解题中的应用,要注意两个定义的区别和联系。
2、利用圆锥曲线的定义和性质解题时,要注意曲线之间的共性和个性。
3、利用圆锥曲线的定义和性质解题时,要加强数形结合、化归思想的训练,以得到解题的最佳途径。
再见
(2)求与双曲线 有共同渐近线,且过点(-3, )的双曲线方程;
(3)一动圆M和直线l:x=-2相切,并且经过点F(2,0),则圆心M的轨迹方程是 .课前热身一、知识回顾 圆 锥 曲 线椭圆双曲线抛物线标准方程几何性质标准方程几何性质标准方程几何性质第二定义第二定义统一定义综合应用椭圆、双曲线、抛物线的标准方程和图形性质椭圆、双曲线、抛物线的标准方程和图形性质例1.求双曲线9y – 16x =144的实半轴与虚半轴长,焦点坐标,离心率及渐进线方程.22
故 渐进线方程为:y=±-x
解:把方程化成标准方程: -- -=1 y
16 x
2522故 实半轴长a=4,虚半轴长b=3∴ c=√16+9 =5.________∴ e=-5
43
4二、应用举例 例2.直线y=x-2与抛物线y2=2x相交于A、B 求证:OA⊥OB。 证法1:将y=x-2代入y2=2x中,得 (x-2)2=2x化简得 x2-6x+4=0解得:则: ∴OA⊥OB证法2:同证法1得方程 x2-6x+4=0由一元二次方程根与系数的关系,可知 x1+x2=6, x1·x2=4 ∴OA⊥OB∵y1=x1-2 , y2=x2-2;∴y1·y2=(x1-2)(x2-2)=x1·x2-2(x1+x2)+4
=4-12+4=-4 例3.一圆与圆x2+y2+6x+5=0外切,同时与圆x2+y2-6x-91=0内切,求动圆圆心的轨迹方程,并说明它是什么样的曲线解法1:如图:设动圆圆心为P(x,y),半径为R,两已知圆圆心为O1、O2。分别将两已知圆的方程
x2+y2+6x+5=0 x2+y2-6x-91=0
配方,得 (x+3)2+y2=4 (x-3)2+y2=100当⊙P与⊙O1: (x+3)2+y2=4外切时,有 |O1P|=R+2 ①
当⊙P与⊙O2: (x-3)2+y2=100内切时,有 |O2P|=10-R ②①、②式两边分别相加,得 |O1P|+|O2P|=12即化简并整理,得 3x2+4y2-108=0即可得所以,动圆圆心的轨迹是椭圆,它的长轴、短轴分别为解法2:同解法1得方程即,动圆圆心P(x,y)到点O1(-3,0)和点O2(3,0)距离的和是常数12,所以点P的轨迹是焦点为(-3,0)、(3,0),长轴长等于12的椭圆。于是可求出它的标准方程。∵2c=6 ,2a=12 , ∴ c=3 , a=6 ∴b2=36-9=27于是得动圆圆心的轨迹方程为这个动圆圆心的轨迹是椭圆,它的长轴、短轴分别为三、课堂练习 1. 动点P 到直线 x+4=0 的距离减去它到点M(2,0)的距离之差等于2,则点P 的轨迹是 ( )
A.直线 B.椭圆 C.双曲线 D.抛物线D2.P是双曲线 x2/4-y2=1 上任意一点,O为原点,则OP线段中点Q的轨迹方程是( ) 3.和圆x2+y2=1外切,且和x轴相切的动圆圆心O的轨迹方程是 。 x2=2|y|+1B做练习 3.过点P( 0 , 4 )与抛物线y2=2x只有一个公共点的直线有 条。4、直线 y=kx+1与焦点在x轴上的椭圆 x2/5+y2/m=1 总有公共点,则m的取值范围是 。 5、过点M(-2,0)的直线l与椭圆 x2+2y2=2 交于P1、P2两点,线段P1P2的中点为P,设直线 l 的斜率为k1(k1≠0),直线OP的斜率为k2,则 k1k2 的值为 ( ) 3[1,5) 已知椭圆 中,F1、F2 分
别为其 左、右焦点和点A ,试在椭圆上找一点 P,使
(1) 取得最小值;
(2) 取得最小值.AF1F2xyoPP思考题 四、小结:
1、本节课的重点是掌握圆锥曲线的定义及性质在解题中的应用,要注意两个定义的区别和联系。
2、利用圆锥曲线的定义和性质解题时,要注意曲线之间的共性和个性。
3、利用圆锥曲线的定义和性质解题时,要加强数形结合、化归思想的训练,以得到解题的最佳途径。
再见
