四川省广元市2014-2015学年人教版数学选修1-1:3.1.1《变化率与导数》课件
文档属性
| 名称 | 四川省广元市2014-2015学年人教版数学选修1-1:3.1.1《变化率与导数》课件 |  | |
| 格式 | zip | ||
| 文件大小 | 619.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-06-21 14:43:51 | ||
图片预览











文档简介
课件36张PPT。3.1 《变化率与导数》教学目标 了解导数概念的实际背景,体会导数的思想及其内涵
教学重点:
导数概念的实际背景,导数的思想及其内涵变化率问题问题1 气球膨胀率问题2 高台跳水运动中,运动员相对于水面的高度是引导:这一现象中,哪些量在改变?
变量的变化情况?
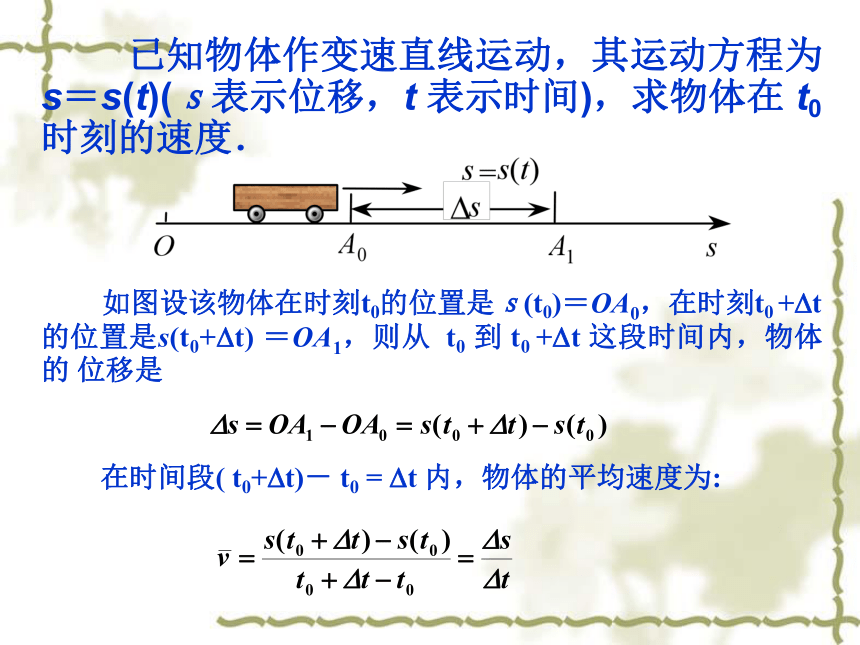
引入气球平均膨胀率的概念当空气容量V从0增加1L时,半径增加了 r(1)-r(0)= 0.62 当空气容量V从1加2L时,半径增加了 r(2)-r(1)= 0.16 探究活动 气球的平均膨胀率是一个特殊的情况,我们把这一思路延伸到函数上,归纳一下得出函数的平均变化率设某个变量 f 随 x 的变化而变化,从 x 经过 △x , 量 f 的改变量为量 f 的平均变化率为平均速度反映了汽车在前10秒内的快慢程度,为了了解汽车的性能,还需要知道汽车在某一时刻的速度——瞬时速度.2. 瞬时速度 平均速度的概念这段时间内汽车的平均速度为 已知物体作变速直线运动,其运动方程为s=s(t)(s表示位移,t 表示时间),求物体在 t0 时刻的速度. 如图设该物体在时刻t0的位置是s(t0)=OA0,在时刻t0 +Dt 的位置是s(t0+Dt) =OA1,则从 t0 到 t0 +Dt 这段时间内,物体的 位移是 在时间段( t0+Dt)- t0 = Dt 内,物体的平均速度为:
要精确地描述非匀速直线运动,就要知道物体在每一时刻运动的快慢程度.如果物体的运动规律是 s =s(t ),那么物体在时刻t 的瞬时速度v,就是物体在t 到 t+Dt 这段时间内,当 Dt?0 时平均速度.的极限.即 例 物体作自由落体运动,
运动方程为: ,其中位移
单位是m ,时间单位是s ,g=9.8m/s2.
求:(1) 物体在时间区间 [2,2.1]上的平均速度;
(2) 物体在时间区间[2,2.01]上的平均速度;
(3) 物体在t =2时的瞬时速度. (1) 将 Dt=0.1代入上式,得 (2) 将 Dt=0.01代入上式,得瞬时速度高台跳水高台跳水导数的概念一般地,函数 y =f(x) 在点x=x0处的瞬时变化率是导数的概念也可记作 若这个极限不存在,则称在点x0 处不可导。
设函数 y = f(x) 在点 x=x0 的附近有定义,当自变量 x 在 x0 处取得增量 △x ( 点 x0 +△x 仍在该定义内)时, 相应地函数 y 取得增量 △y = f (x0 +△x)- f (x0 ),若△y与△x之比当 △x→0的极限存在,则称函数 y = f(x)在点 x0 处可导 ,并称这个极限为函数 y = f(x)在点 x0 处的导数, 记为 。即例:
高台跳水运动中, 秒 时运动员相
对于水面的高度是
(单位: ),求运动员在 时的瞬时
速度,并解释此时的运动状态;在 呢?
同理, 运动员在 时的瞬时速度为 ,上升下落这说明运动员在 附近,正以大约 的速率 。1.你能借助函数 的图象说说平均变化率表示什么吗?请在函数图象中画出来.割线AB的的变化情况2.在 的过程中, 请在函数图象中画出来. 你能描述一下吗?3.1.1 导数的几何意义的切线方程为即
圆的切线定义并不适用于一般的曲线。
通过逼近的方法,将割线趋于的确定位置的直线定义为切线(交点可能不惟一)适用于各种曲线。所以,这种定义才真正反映了切线的直观本质。
根据导数的几何意义,在点P附近,曲线可以
用在点P处的切线近似代替 。
大多数函数曲线就一小范围来看,大致可看作直线,所以,某点附近的曲线可以用过此点的切线近似代替,即“以直代曲” (以简单的对象刻画复杂的对象)
1.在函数 的
图像上,(1)用图形来体现导数 ,
的几何意义. (2)请描述,比较曲线分别在 附近增(减)以及增(减)快慢的情况。
在 附近呢? (2)请描述,比较曲线分别在 附近增(减)以及增(减)快慢的情况。
在 附近呢? 增(减):增(减)快慢:=切线的斜率附近:瞬时变化率(正或负)即:瞬时变化率(导数)(数形结合,以直代曲)画切线即:导数的绝多值的大小=切线斜率的绝对值的
大小切线的倾斜程度
(陡峭程度)以简单对象刻画复杂的对象(2) 曲线在 时,切线平行于x轴,曲线在
附近比较平坦,几乎没有升降. 曲线在 处切线 的斜率 0
在 附近,曲线 ,函数在
附近单调 如图,切线 的倾斜程度大于切线 的
倾斜程度, 大于上升递增上升 这说明曲线在 附近比在 附近
得迅速. 递减下降小于下降
2.如图表示人体血管中的药物浓度c=f(t)
(单位:mg/ml)随时间t(单位:min)
变化的函数图像,根据图像,估计
t=0.2,0.4,0.6,0.8(min)时,血管中
药物浓度的瞬时变化率,把数据用表格
的形式列出。(精确到0.1)
血管中药物浓度的瞬时变化率,就是药物浓度从图象上看,它表示曲线在该点处的切线的斜率.函数f(t)在此时刻的导数,(数形结合,以直代曲)以简单对象刻画复杂的对象
抽象概括:
是确定的数是 的函数 导函数 的概念:小结:
1.函数 在 处的导数
的几何意义,就是函数 的图像在点
处的切线AD的斜率(数形结合)
=切线 AD的斜率3.导函数(简称导数) 2.利用导数的几何意义解释实际生活问题,体会“数形结合”,“以直代曲”的数学
思想方法。 以简单对象刻画复杂的对象再见
教学重点:
导数概念的实际背景,导数的思想及其内涵变化率问题问题1 气球膨胀率问题2 高台跳水运动中,运动员相对于水面的高度是引导:这一现象中,哪些量在改变?
变量的变化情况?
引入气球平均膨胀率的概念当空气容量V从0增加1L时,半径增加了 r(1)-r(0)= 0.62 当空气容量V从1加2L时,半径增加了 r(2)-r(1)= 0.16 探究活动 气球的平均膨胀率是一个特殊的情况,我们把这一思路延伸到函数上,归纳一下得出函数的平均变化率设某个变量 f 随 x 的变化而变化,从 x 经过 △x , 量 f 的改变量为量 f 的平均变化率为平均速度反映了汽车在前10秒内的快慢程度,为了了解汽车的性能,还需要知道汽车在某一时刻的速度——瞬时速度.2. 瞬时速度 平均速度的概念这段时间内汽车的平均速度为 已知物体作变速直线运动,其运动方程为s=s(t)(s表示位移,t 表示时间),求物体在 t0 时刻的速度. 如图设该物体在时刻t0的位置是s(t0)=OA0,在时刻t0 +Dt 的位置是s(t0+Dt) =OA1,则从 t0 到 t0 +Dt 这段时间内,物体的 位移是 在时间段( t0+Dt)- t0 = Dt 内,物体的平均速度为:
要精确地描述非匀速直线运动,就要知道物体在每一时刻运动的快慢程度.如果物体的运动规律是 s =s(t ),那么物体在时刻t 的瞬时速度v,就是物体在t 到 t+Dt 这段时间内,当 Dt?0 时平均速度.的极限.即 例 物体作自由落体运动,
运动方程为: ,其中位移
单位是m ,时间单位是s ,g=9.8m/s2.
求:(1) 物体在时间区间 [2,2.1]上的平均速度;
(2) 物体在时间区间[2,2.01]上的平均速度;
(3) 物体在t =2时的瞬时速度. (1) 将 Dt=0.1代入上式,得 (2) 将 Dt=0.01代入上式,得瞬时速度高台跳水高台跳水导数的概念一般地,函数 y =f(x) 在点x=x0处的瞬时变化率是导数的概念也可记作 若这个极限不存在,则称在点x0 处不可导。
设函数 y = f(x) 在点 x=x0 的附近有定义,当自变量 x 在 x0 处取得增量 △x ( 点 x0 +△x 仍在该定义内)时, 相应地函数 y 取得增量 △y = f (x0 +△x)- f (x0 ),若△y与△x之比当 △x→0的极限存在,则称函数 y = f(x)在点 x0 处可导 ,并称这个极限为函数 y = f(x)在点 x0 处的导数, 记为 。即例:
高台跳水运动中, 秒 时运动员相
对于水面的高度是
(单位: ),求运动员在 时的瞬时
速度,并解释此时的运动状态;在 呢?
同理, 运动员在 时的瞬时速度为 ,上升下落这说明运动员在 附近,正以大约 的速率 。1.你能借助函数 的图象说说平均变化率表示什么吗?请在函数图象中画出来.割线AB的的变化情况2.在 的过程中, 请在函数图象中画出来. 你能描述一下吗?3.1.1 导数的几何意义的切线方程为即
圆的切线定义并不适用于一般的曲线。
通过逼近的方法,将割线趋于的确定位置的直线定义为切线(交点可能不惟一)适用于各种曲线。所以,这种定义才真正反映了切线的直观本质。
根据导数的几何意义,在点P附近,曲线可以
用在点P处的切线近似代替 。
大多数函数曲线就一小范围来看,大致可看作直线,所以,某点附近的曲线可以用过此点的切线近似代替,即“以直代曲” (以简单的对象刻画复杂的对象)
1.在函数 的
图像上,(1)用图形来体现导数 ,
的几何意义. (2)请描述,比较曲线分别在 附近增(减)以及增(减)快慢的情况。
在 附近呢? (2)请描述,比较曲线分别在 附近增(减)以及增(减)快慢的情况。
在 附近呢? 增(减):增(减)快慢:=切线的斜率附近:瞬时变化率(正或负)即:瞬时变化率(导数)(数形结合,以直代曲)画切线即:导数的绝多值的大小=切线斜率的绝对值的
大小切线的倾斜程度
(陡峭程度)以简单对象刻画复杂的对象(2) 曲线在 时,切线平行于x轴,曲线在
附近比较平坦,几乎没有升降. 曲线在 处切线 的斜率 0
在 附近,曲线 ,函数在
附近单调 如图,切线 的倾斜程度大于切线 的
倾斜程度, 大于上升递增上升 这说明曲线在 附近比在 附近
得迅速. 递减下降小于下降
2.如图表示人体血管中的药物浓度c=f(t)
(单位:mg/ml)随时间t(单位:min)
变化的函数图像,根据图像,估计
t=0.2,0.4,0.6,0.8(min)时,血管中
药物浓度的瞬时变化率,把数据用表格
的形式列出。(精确到0.1)
血管中药物浓度的瞬时变化率,就是药物浓度从图象上看,它表示曲线在该点处的切线的斜率.函数f(t)在此时刻的导数,(数形结合,以直代曲)以简单对象刻画复杂的对象
抽象概括:
是确定的数是 的函数 导函数 的概念:小结:
1.函数 在 处的导数
的几何意义,就是函数 的图像在点
处的切线AD的斜率(数形结合)
=切线 AD的斜率3.导函数(简称导数) 2.利用导数的几何意义解释实际生活问题,体会“数形结合”,“以直代曲”的数学
思想方法。 以简单对象刻画复杂的对象再见
