四川省广元市2014-2015学年人教版数学选修1-1:3.3.1《导数在研究函数中的应用-单调性》课件
文档属性
| 名称 | 四川省广元市2014-2015学年人教版数学选修1-1:3.3.1《导数在研究函数中的应用-单调性》课件 |  | |
| 格式 | zip | ||
| 文件大小 | 171.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-06-21 14:46:10 | ||
图片预览




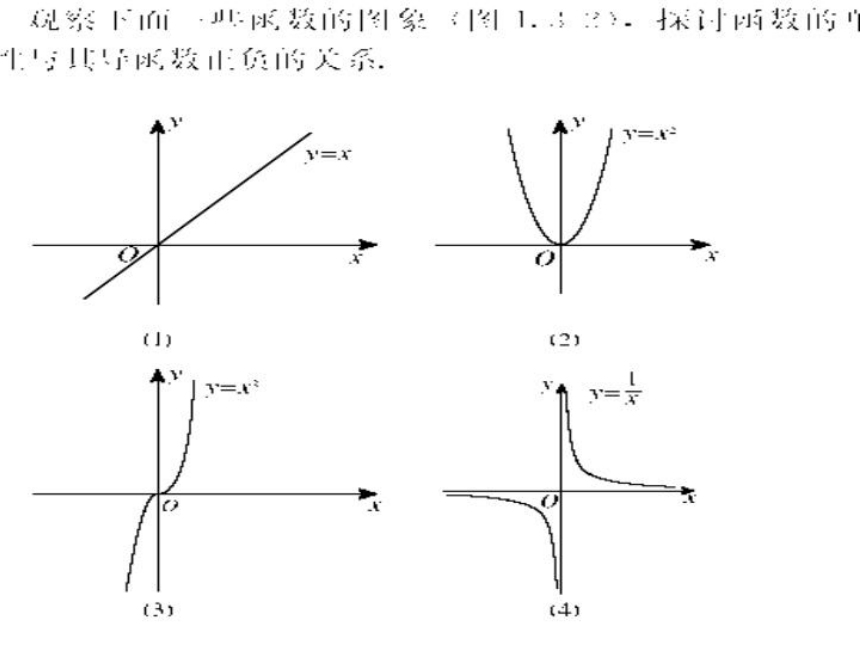
文档简介
课件14张PPT。3.3.1《导数在研究
函数中的应用-单调性》教学目标 1.正确理解利用导数判断函数的单调性的原理;
2.掌握利用导数判断函数单调性的方法
教学重点:
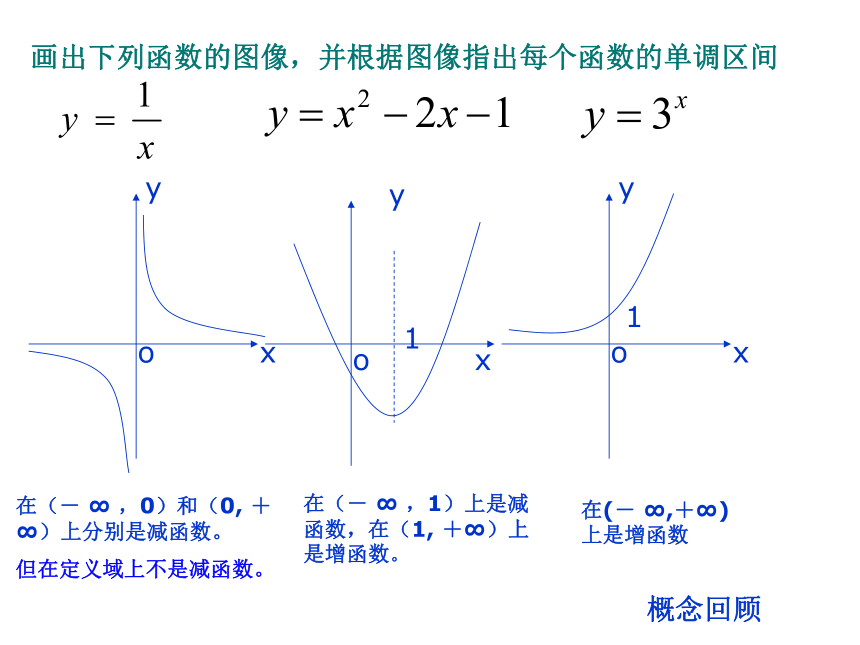
利用导数判断函数单调性. 函数的单调性与导数在(- ∞ ,0)和(0, +∞)上分别是减函数。
但在定义域上不是减函数。在(- ∞ ,1)上是减函数,在(1, +∞)上是增函数。在(- ∞,+∞)上是增函数概念回顾画出下列函数的图像,并根据图像指出每个函数的单调区间单调性的概念对于给定区间上的函数f(x):
1.如果对于这个区间上的任意两个自变量x1,x2,当x1f(x2),那么就说f(x)在这个区间上是减函数对于函数y=f(x)在某个区间上单调递增或单调递减的性质,叫做f(x)在这个区间上的单调性,这个区间叫做f(x)的单调区间。
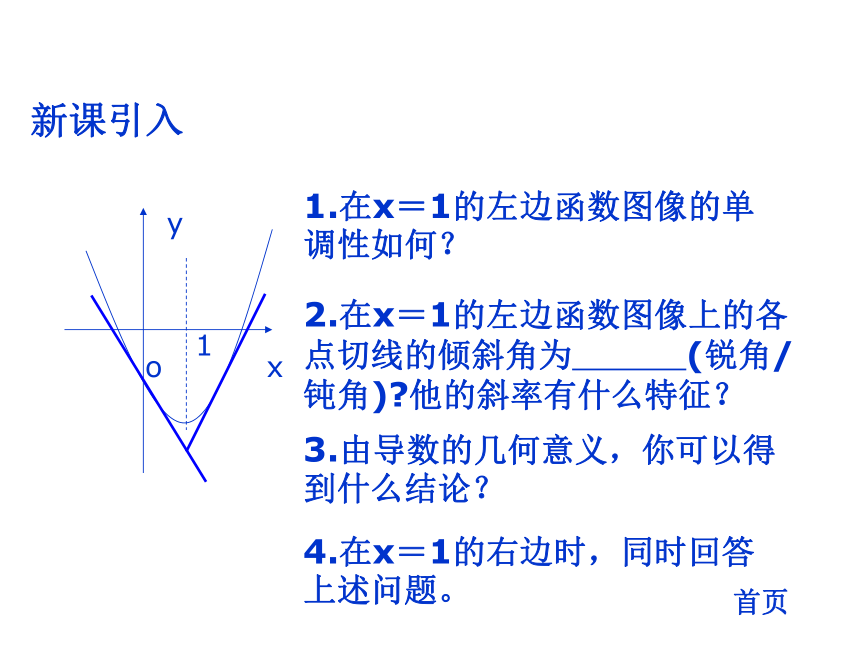
y1.在x=1的左边函数图像的单调性如何?新课引入首页2.在x=1的左边函数图像上的各点切线的倾斜角为 (锐角/钝角)?他的斜率有什么特征?3.由导数的几何意义,你可以得到什么结论?4.在x=1的右边时,同时回答上述问题。定理:
一般地,函数y=f(x)在某个区间内可导:
如果恒有 f′(x)>0,则 f(x) 是增函数。
如果恒有 f′(x)<0,则f(x) 是减函数。
如果恒有 f′(x)=0,则f(x) 是常数。
例1.确定函数 在哪个区间是减函数?在哪个区间上是增函数?解: (1)求函数的定义域
函数f (x)的定义域是(- ∞,+∞)(2)求函数的导数
(3)令 以及
求自变量x的取值范围,也即函数的单调区间。令2x-4>0,解得x>2
∴x∈(2,+∞)时, 是增函数
令2x-4<0,解得x<2
∴x∈(-∞,2)时, 是减函数
确定函数 ,在哪个区间是增函数,那个区间是减函数。解:函数f(x)的定义域是(- ∞,+∞)
令6x2-12x>0,解得x>2或x<0
∴当x ∈(2,+∞)时,f(x)是增函数;
当x ∈(-∞,0)时,f(x)也是增函数
令6x2-12x<0,解得,0∴当x ∈(0,2)时,f(x)是减函数。首页知识点:定理:
一般地,函数y=f(x)在某个区间内可导:
如果恒有 ,则 f(x)在是增函数。
如果恒有 ,则 f(x)是减函数。
如果恒有 ,则 f(x)是常数。
步骤:
(1)求函数的定义域
(2)求函数的导数
(3)令f’(x)>0以及f’(x)<0,求自变量x的取值范围,即函数的单调区间。f’(x)>0f’(x)<0f’(x)=0练习:判断下列函数的单调性(1)f(x)=x3+3x;
(2)f(x)=sinx-x,x∈(0,π);
(3)f(x)=2x3+3x2-24x+1;
(4)f(x)=ex-x;
再见
2.掌握利用导数判断函数单调性的方法
教学重点:
利用导数判断函数单调性. 函数的单调性与导数在(- ∞ ,0)和(0, +∞)上分别是减函数。
但在定义域上不是减函数。在(- ∞ ,1)上是减函数,在(1, +∞)上是增函数。在(- ∞,+∞)上是增函数概念回顾画出下列函数的图像,并根据图像指出每个函数的单调区间单调性的概念对于给定区间上的函数f(x):
1.如果对于这个区间上的任意两个自变量x1,x2,当x1
y1.在x=1的左边函数图像的单调性如何?新课引入首页2.在x=1的左边函数图像上的各点切线的倾斜角为 (锐角/钝角)?他的斜率有什么特征?3.由导数的几何意义,你可以得到什么结论?4.在x=1的右边时,同时回答上述问题。定理:
一般地,函数y=f(x)在某个区间内可导:
如果恒有 f′(x)>0,则 f(x) 是增函数。
如果恒有 f′(x)<0,则f(x) 是减函数。
如果恒有 f′(x)=0,则f(x) 是常数。
例1.确定函数 在哪个区间是减函数?在哪个区间上是增函数?解: (1)求函数的定义域
函数f (x)的定义域是(- ∞,+∞)(2)求函数的导数
(3)令 以及
求自变量x的取值范围,也即函数的单调区间。令2x-4>0,解得x>2
∴x∈(2,+∞)时, 是增函数
令2x-4<0,解得x<2
∴x∈(-∞,2)时, 是减函数
确定函数 ,在哪个区间是增函数,那个区间是减函数。解:函数f(x)的定义域是(- ∞,+∞)
令6x2-12x>0,解得x>2或x<0
∴当x ∈(2,+∞)时,f(x)是增函数;
当x ∈(-∞,0)时,f(x)也是增函数
令6x2-12x<0,解得,0
一般地,函数y=f(x)在某个区间内可导:
如果恒有 ,则 f(x)在是增函数。
如果恒有 ,则 f(x)是减函数。
如果恒有 ,则 f(x)是常数。
步骤:
(1)求函数的定义域
(2)求函数的导数
(3)令f’(x)>0以及f’(x)<0,求自变量x的取值范围,即函数的单调区间。f’(x)>0f’(x)<0f’(x)=0练习:判断下列函数的单调性(1)f(x)=x3+3x;
(2)f(x)=sinx-x,x∈(0,π);
(3)f(x)=2x3+3x2-24x+1;
(4)f(x)=ex-x;
再见
