4.5 利用三角形全等测距离同步练习(含答案)
文档属性
| 名称 | 4.5 利用三角形全等测距离同步练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 808.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-16 13:36:22 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
4.5利用三角形全等测距离
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,△ABC≌△A'B'C,∠ACB90°,∠A'CB20°,则∠BCB'的度数是( )
A.60° B.70° C.80° D.90°
2.如图,在△ABC中,AC⊥CB,CD平分∠ACB,点E在AC上,且CE=CB,则下列结论:①DC平分∠BDE;②BD=DE;③∠B=∠CED;④∠A+∠CED=90°,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
3.如图,△ACB≌△,∠BC=30°,则∠AC的度数为( )
A.20° B.30° C.35° D.40°
4.如下图,点E,F是线段上的两点,如果,且,,则的长等于( )
A.3 B.4 C.5 D.6
5.如图,,则的度数是( )
A.
B.
C.
D.
6.如图,△ABD≌△ACE,AB=9,AD=7,BD=8,则BE的长是( )
A.1 B.2 C.4 D.6
7.下列说法中,不正确的是
全等形的面积相等;
形状相同的两个三角形是全等三角形;
全等三角形的对应边,对应角相等;
若两个三角形全等,则其中一个三角形一定是由另一个三角形旋转得到的.
A.与 B.与 C.与 D.与
8.下列说法:①有两边和一角对应相等的两个三角形全等;②有一角为80°,且腰长相等的两个等腰三角形全等;③有两边对应相等的两个直角三角形全等;④有两边及第三边上的高对应相等的两个三角形全等.其中错误的有( )
A.1个 B.2个 C.3个 D.4个
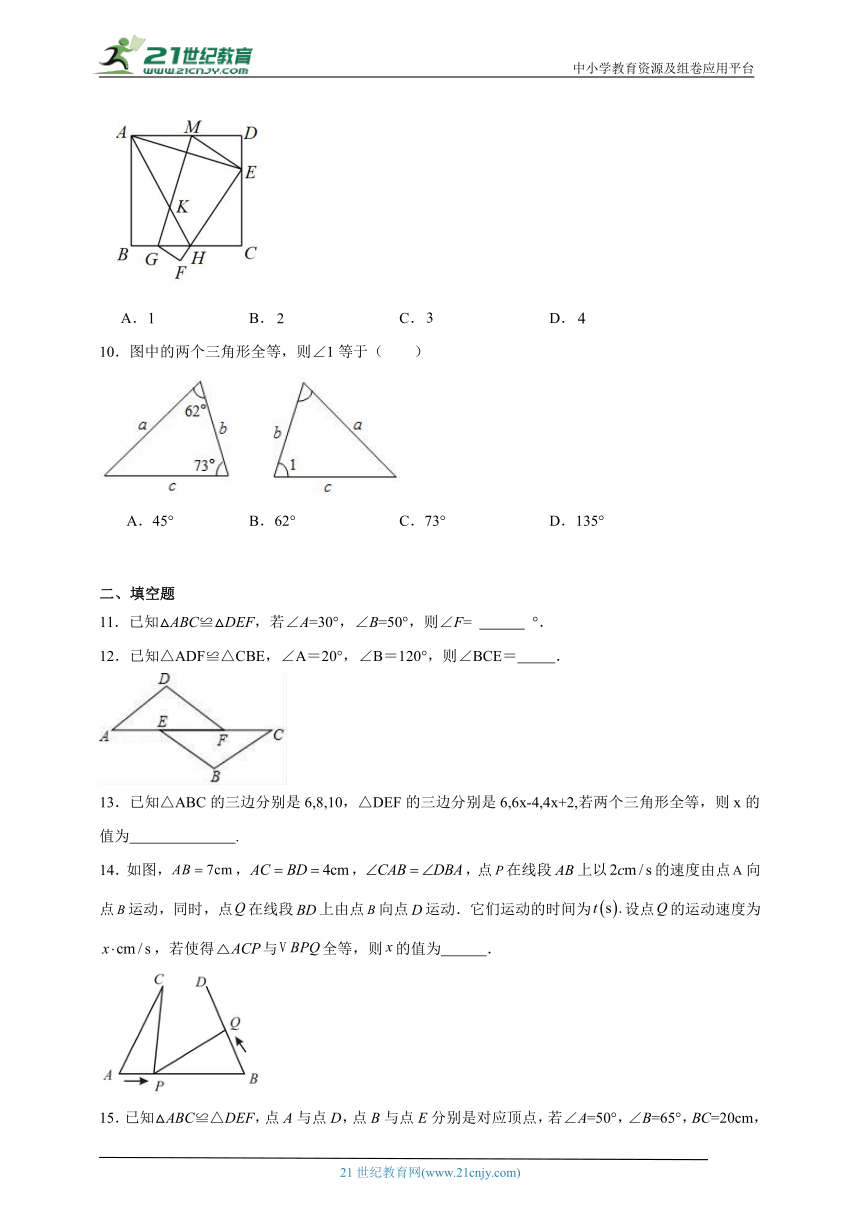
9.如图,在正方形纸片中,点为正方形边上的一点不与点,点重合,将正方形纸片折叠,使点落在点处,点落在点处,交于点,折痕为,连接、,交于点下列结论:①是等腰三角形;②;③平分;④;⑤,其中正确结论的个数是( )
A. B. C. D.
10.图中的两个三角形全等,则∠1等于( )
A.45° B.62° C.73° D.135°
二、填空题
11.已知△ABC≌△DEF,若∠A=30°,∠B=50°,则∠F= °.
12.已知△ADF≌△CBE,∠A=20°,∠B=120°,则∠BCE= .
13.已知△ABC的三边分别是6,8,10,△DEF的三边分别是6,6x-4,4x+2,若两个三角形全等,则x的值为 .
14.如图,,,,点在线段上以的速度由点向点运动,同时,点在线段上由点向点运动.它们运动的时间为设点的运动速度为,若使得与全等,则的值为 .
15.已知△ABC≌△DEF,点A与点D,点B与点E分别是对应顶点,若∠A=50°,∠B=65°,BC=20cm,则∠F= .
16.如图,若△ABE≌△ACD,且∠A=65°,∠C=20°,则∠AEB= °.
17.如图,Rt△ABC中,AB=AC,点D为BC中点.∠MDN=90°,∠MDN绕点D旋转,DM、DN分别与边AB、AC交于E、F两点.下列结论:
①△DEF是等腰直角三角形;
②AE=CF;
③△BDE≌△ADF;
④BE+CF=EF;
⑤S四边形AEDF=AD2,
其中正确结论是 (填序号)
18.一个三角形的三条边长分别为,,,另一个三角形的三条边长分别为,,,若这两个三角形全等,则 .
19.如图,,,,,则的周长为 .
20.如图,若,,,则的长为 .
三、解答题
21.已知是四边形内一点,且,,是的中点.
(1)如图,连接,,若,求证:;
(2)如图,连接,若,求证:;
(3)如图,若,,垂足为,求证:点,,在同一条直线上.
22.如图,,,点在上,且.求证:.
23.如图,点A是线段DE上一点,∠BAC=90°,AB=AC,BD⊥DE,CE⊥DE.
(1)求证:DE=BD+CE.
(2)如果是如图2这个图形,BD、CE、DE有什么数量关系?并证明.
24.如图,在中,,点、分别在、上,,、相交于点.
(1)求证:;
(2)求证:.
25.阅读与思考
下面是小明同学的数学学习笔记,请您仔细阅读并完成相应的任务:构造全等三角形解决图形与几何问题
在图形与几何的学习中,常常会遇到一些问题无法直接解答,需要添加辅助线才能解决.比如下面的题目中出现了角平分线和垂线段,我们可以通过延长垂线段与三角形的一边相交构造全等三角形,运用全等三角形的性质解决问题.
例:如图1,是内一点,且平分,,连接,若的面积为10,求的面积.
该问题的解答过程如下:
解:如图2,过点作交延长线于点,、交于点,
平分,
.
,
.
在和中,,
(依据1)
(依据2),,
,.
……
任务一:上述解答过程中的依据1,依据2分别是___________,___________;
任务二:请将上述解答过程的剩余部分补充完整;
应用:如图3,在中,,,平分交于点,过点作交延长线于点.若,求的长.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
4.5利用三角形全等测距离
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,△ABC≌△A'B'C,∠ACB90°,∠A'CB20°,则∠BCB'的度数是( )
A.60° B.70° C.80° D.90°
2.如图,在△ABC中,AC⊥CB,CD平分∠ACB,点E在AC上,且CE=CB,则下列结论:①DC平分∠BDE;②BD=DE;③∠B=∠CED;④∠A+∠CED=90°,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
3.如图,△ACB≌△,∠BC=30°,则∠AC的度数为( )
A.20° B.30° C.35° D.40°
4.如下图,点E,F是线段上的两点,如果,且,,则的长等于( )
A.3 B.4 C.5 D.6
5.如图,,则的度数是( )
A.
B.
C.
D.
6.如图,△ABD≌△ACE,AB=9,AD=7,BD=8,则BE的长是( )
A.1 B.2 C.4 D.6
7.下列说法中,不正确的是
全等形的面积相等;
形状相同的两个三角形是全等三角形;
全等三角形的对应边,对应角相等;
若两个三角形全等,则其中一个三角形一定是由另一个三角形旋转得到的.
A.与 B.与 C.与 D.与
8.下列说法:①有两边和一角对应相等的两个三角形全等;②有一角为80°,且腰长相等的两个等腰三角形全等;③有两边对应相等的两个直角三角形全等;④有两边及第三边上的高对应相等的两个三角形全等.其中错误的有( )
A.1个 B.2个 C.3个 D.4个
9.如图,在正方形纸片中,点为正方形边上的一点不与点,点重合,将正方形纸片折叠,使点落在点处,点落在点处,交于点,折痕为,连接、,交于点下列结论:①是等腰三角形;②;③平分;④;⑤,其中正确结论的个数是( )
A. B. C. D.
10.图中的两个三角形全等,则∠1等于( )
A.45° B.62° C.73° D.135°
二、填空题
11.已知△ABC≌△DEF,若∠A=30°,∠B=50°,则∠F= °.
12.已知△ADF≌△CBE,∠A=20°,∠B=120°,则∠BCE= .
13.已知△ABC的三边分别是6,8,10,△DEF的三边分别是6,6x-4,4x+2,若两个三角形全等,则x的值为 .
14.如图,,,,点在线段上以的速度由点向点运动,同时,点在线段上由点向点运动.它们运动的时间为设点的运动速度为,若使得与全等,则的值为 .
15.已知△ABC≌△DEF,点A与点D,点B与点E分别是对应顶点,若∠A=50°,∠B=65°,BC=20cm,则∠F= .
16.如图,若△ABE≌△ACD,且∠A=65°,∠C=20°,则∠AEB= °.
17.如图,Rt△ABC中,AB=AC,点D为BC中点.∠MDN=90°,∠MDN绕点D旋转,DM、DN分别与边AB、AC交于E、F两点.下列结论:
①△DEF是等腰直角三角形;
②AE=CF;
③△BDE≌△ADF;
④BE+CF=EF;
⑤S四边形AEDF=AD2,
其中正确结论是 (填序号)
18.一个三角形的三条边长分别为,,,另一个三角形的三条边长分别为,,,若这两个三角形全等,则 .
19.如图,,,,,则的周长为 .
20.如图,若,,,则的长为 .
三、解答题
21.已知是四边形内一点,且,,是的中点.
(1)如图,连接,,若,求证:;
(2)如图,连接,若,求证:;
(3)如图,若,,垂足为,求证:点,,在同一条直线上.
22.如图,,,点在上,且.求证:.
23.如图,点A是线段DE上一点,∠BAC=90°,AB=AC,BD⊥DE,CE⊥DE.
(1)求证:DE=BD+CE.
(2)如果是如图2这个图形,BD、CE、DE有什么数量关系?并证明.
24.如图,在中,,点、分别在、上,,、相交于点.
(1)求证:;
(2)求证:.
25.阅读与思考
下面是小明同学的数学学习笔记,请您仔细阅读并完成相应的任务:构造全等三角形解决图形与几何问题
在图形与几何的学习中,常常会遇到一些问题无法直接解答,需要添加辅助线才能解决.比如下面的题目中出现了角平分线和垂线段,我们可以通过延长垂线段与三角形的一边相交构造全等三角形,运用全等三角形的性质解决问题.
例:如图1,是内一点,且平分,,连接,若的面积为10,求的面积.
该问题的解答过程如下:
解:如图2,过点作交延长线于点,、交于点,
平分,
.
,
.
在和中,,
(依据1)
(依据2),,
,.
……
任务一:上述解答过程中的依据1,依据2分别是___________,___________;
任务二:请将上述解答过程的剩余部分补充完整;
应用:如图3,在中,,,平分交于点,过点作交延长线于点.若,求的长.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
