2023-2024学年人教版八年级数学上册 第12章全等三角形 期末复习解答题专题提升训练(含答案)
文档属性
| 名称 | 2023-2024学年人教版八年级数学上册 第12章全等三角形 期末复习解答题专题提升训练(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 483.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-17 12:35:53 | ||
图片预览




文档简介
2023-2024学年人教版八年级数学上册《第12章全等三角形》
期末复习解答题专题提升训练(附答案)
1.已知三角形的两个角分别是和,这两角所夹的边等于,如图所示,求作,使,,.(不写作法,保留作图痕迹)
2.如图,已知中,,.
(1)尺规作图:作的角平分线,交于点D(不写作法,保留作图痕迹).
(2)求的度数.
3.如图,相交于点O,,,连接,求证:.
4.如图,点C、E、B、F在一条直线上,于B,于E,,,求证:.
5.如图,在中,D为的中点.
(1)求证:;
(2)若,,求的取值范围.
6.已知,如图,在中,,,直线交于F,交于E,交的延长线于D,且,连接、,则与之间有何关系?请证明你的结论.
7.如图,在中,平分,于点E,点F在上,.
(1)求证:.
(2)若,求的长.
8.如图,已知,点分别在上,,.
(1)求证:;
(2)求证:.
9.如图,某校八年级(3)班的学生为了测量学校一幢教学楼的高度,在旗杆与楼之间选定一点P.用测角仪测得旗杆顶C视线与地面夹角,测楼顶A视线与地面夹角,量得P到楼底的距离与旗杆高度相等,等于10米,量得旗杆与楼之间距离为米,这样就可以计算出楼高了,楼高是多少米?
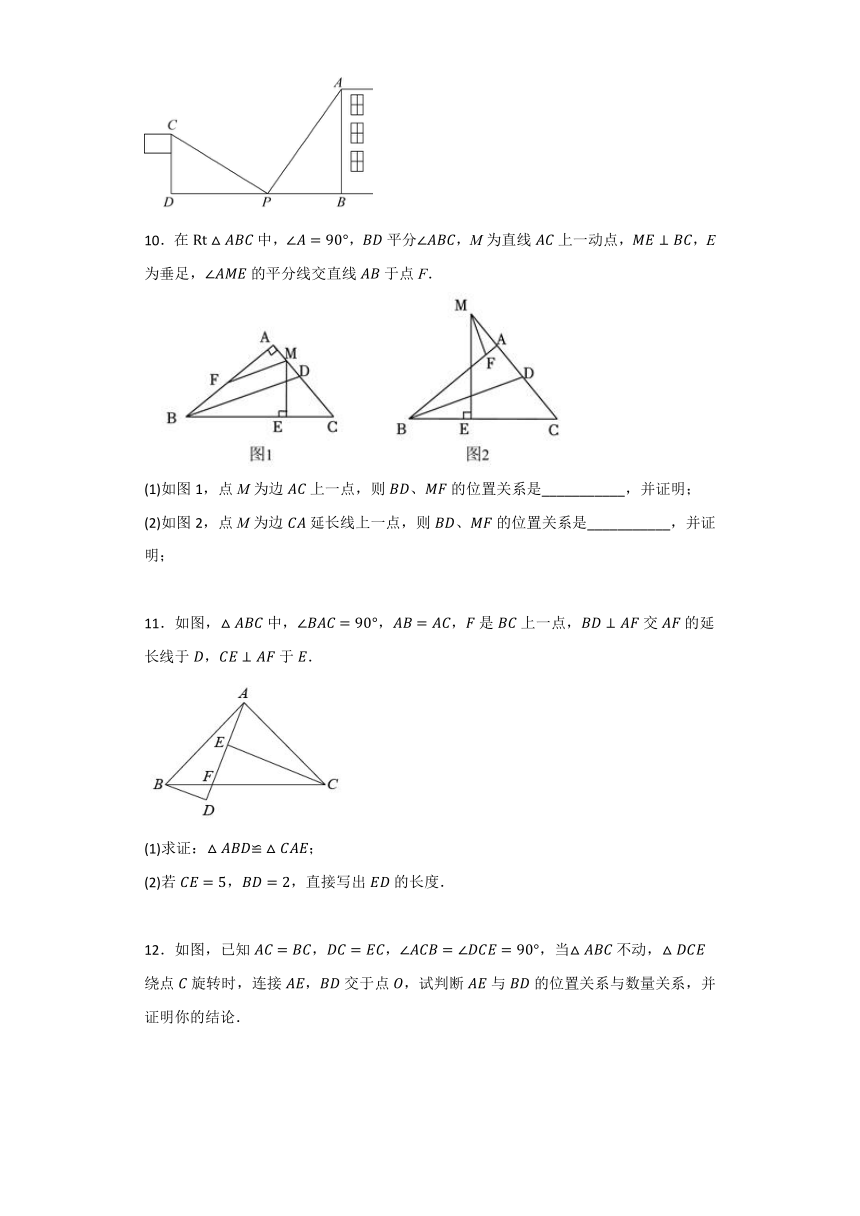
10.在中,,平分,M为直线上一动点,,E为垂足,的平分线交直线于点F.
(1)如图1,点M为边上一点,则的位置关系是___________,并证明;
(2)如图2,点M为边延长线上一点,则的位置关系是___________,并证明;
11.如图,中,,,是上一点,交的延长线于,于.
(1)求证:;
(2)若,,直接写出的长度.
12.如图,已知,,,当不动,绕点旋转时,连接,交于点,试判断与的位置关系与数量关系,并证明你的结论.
13.已知,如图,在中,,在中,,且,连接BD,CE交于点,连接.
(1)求证:;
(2)求证:.
14.如图,和的角平分线,相交点,.
(1)直接写出= °;
(2)求证:;
(3)若,求证:.
15.三条边都不相等的的和的平分线,相交于点.
(1)求证:;
(2)若,求的度数.
16.已知是的平分线,点P是射线上一定点,点C、D分别在射线、上,连接、.
(1)如图①,当,时,则与的数量关系是___________;
(2)如图②,点C、D在射线、上滑动,且,当时,与在(1)中的数量关系还成立吗?请说明理由.
(3)在问题(2)中,若,则四边形的面积S是否为定值?若是,请求出该定值,若不是,请说明理由.
17.在学习全等三角形的知识时,数学兴趣小组拿了两个大小不同的等腰直角三角板进行拼摆,并探究摆放后所构成的图形之间的关系,如图1,在和中,.
(1)勤奋小组摆出如图2所示的图形,点A和点D重合,连接和,求证:.
(2)超越小组在勤奋小组的启发下,把两个三角形板按如图3的方式摆放,点B,C,E在同一直线上,连接,他们发现了和之间的数量和位置关系,请写出这些关系,并说明理由.
18.如图1,在中,,点是直线上一点不与点、重合,以为一边在的右侧作,使,连接.设,.
(1)当点在线段上运动时,
①当时,则是多少?
②猜想与之间的数量关系,并对你的结论进行证明;
(2)如图2,当点在线段的反向延长线上运动时,猜想与之间的数量关系,并对你的结论给出证明.
(3)根据以往学习经验,点还可能在什么位置?请画出图形,直接写出与之间的数量关系.
19.问题背景:
(1)如图1,已知中,,,直线m经过点A,⊥直线m,⊥直线m,垂足分别为点D、E.求证:.
拓展延伸:
(2)如图2,将(1)中的条件改为:在中,,D、A、E三点都在直线m上,并且有.请写出、、三条线段的数量关系,并证明.
实际应用:
(3)如图3,在中,,,点C的坐标为,点A的坐标为,请直接写出B点的坐标.
20.【问题背景】
在四边形中,,,,、分别是、上的点,且,试探究图1中线段、、之间的数量关系.
【初步探索】
小亮同学认为:延长到点,使,连接,先证明,再证明,则可得到、、之间的数量关系是 ________________ .
【探索延伸】
在四边形中如图2,,,、分别是、上的点,,上述结论是否仍然成立?说明理由.
【结论运用】
如图3,在某次军事演习中,舰艇甲在指挥中心(处)北偏西的处,舰艇乙在指挥中心南偏东的处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以60海里/小时的速度前进,舰艇乙沿北偏东的方向以80海里/小时的速度前进1.5小时后,指挥中心观测到甲、乙两舰艇分别到达、处,且两舰艇之间的夹角()为,试求此时两舰艇之间的距离.
参考答案:
1.解:如图所示,即为所求.
2.解:(1)作图如图所示
(2)∵AD是的角平分线,
∴,
由三角形的外角等于与它不相邻的两个内角的和,
得,
∴.
3.证明:在和中,
,
∴.
∴.
4.证明:∵,,
∴,
在和中,
,
∴,
∴,
∴,
即:.
5.(1)证明:延长至点E,使,连接,
∵D为的中点,
∴,
又∵,,
∴,
∴,
∵,
∴.
(2)解:∵,
∵,
∴,
∴,
∵,,
∴,
∴.
6.解:,
理由如下:如图,∵,∴,
∴在与中,
∴(SAS),
∴,
延长交于点,
∵,∴,∴
∴.
7.(1)证明:∵平分,于点E,
∴.
在与中,
,
∴,
∴.
(2)解:设,则,
∵平分,于点E,
∴.
在与中,
,
∴,
∴,即,
解得,即.
8.(1)解: 证明:在和中,
∴ .
(2)解:由(1)知,
∴ ,
在和中,
∴ ,
∴.
9.解:∵,
,
,
∴,
在和中,
∵,
∴,
∴,
∵,
,
∴,
答:楼高是26米.
10.解:(1),理由如下:
过点作,
,,,
,
,
,
,
,
,
;
(2),理由如下:
延长交于点,
,,
,
.
,
,
.
11.(1)证明:.
.
,.
.
.
.
同角的余角相等,
在和中,
,
∴;
(2)∵,
,,
.
12.解:,,证明如下:
,
,即,
在和中,,
,
,,
又,
,
,即,
,
.
13.(1)解:证明:,
,
即,
在和中,
,
;
(2)如图,作于,作于.
由,
,,
,
,
点在平分线上,
平分,即.
14.解:(1),分别平分和,
,,
.
故答案为:120;
(2)过作,,,
,分别平分和,
,,
,
,,
,
,
,
,
在和中,
,
,
;
(3)如图,作的平分线交于点,则,
,,
,,
,,
,,
,
,,
,
,
在和中,
,
,
.
15.(1)证明:,分别是和的平分线,
,
,即,
.
(2)解:如图,过点作于点,作于点,连接,
则,
三条边都不相等的的和的平分线,相交于点,
是的角平分线,
,
在和中,,
,
,
,
由对顶角相等和(1)可知,,
,
又,
,
解得.
16.(1)解:∵是的平分线,
∴,
∵,,
∴,
在和中,
,
∴,
∴,
故答案为:.
(2)成立,理由如下:
过点P作于点E,于点F,
∵是的平分线,
∴,
∵,,
∴,
在和中,
,
∴,
∴,
∵,,,
∴,则,
∵,
∴,
∴,
在和中,
,
∴,
∴,
(3)由(2)可得:,
∴,
∵,
∴,
∵,
∴,
∵.
∴四边形的面积S为定值9.
17.(1)证明:∵,
∴,,
∴.
在和中,,
∴,
∴.
(2).理由如下:
∵,
∴,
∴,
在和中,
∴,
∴.
∵,
∴,
∴,
∴.
18.(1)解:①,
在与中,
又
四边形的内角和为
.
∵,
∴ .
② .
理由如下:
,
在与中,
又
四边形的内角和为
.
(2).
理由如下:
,,
在与中,
≌
,,
即 .
(3)点可能在的延长线上,图形如下,此时.
理由如下:
,,
在与中,
≌
,,
即 .
19.(1)证明:∵⊥直线m,直线m,
∴.
∵,
∴,
∵,
∴.
∵在和中,
,
∴≌,
∴,,
∴,
即:.
(2)解:数量关系.
理由如下:
在中,,
∵,,
∴,
在和中,
,
∴≌,
∴,,
∴;
(3)如图,作轴于E,轴于F,由(1)可知,≌,
,
∴,,
∴,
∴点B的坐标为.
20.解:初步探索:,
在和中,
,
∴,
∴,,
∵,,
∴,
∴,
∴,
在和中,
,
∴,
∴,
∴;
故答案为:,
探索延伸:结论仍然成立,
证明:延长到,使,连接,
∵,,
∴,
在和中,
,
∴,
∴,,
∵,
∴,
∴,
在和中,
,
∴,
∴,
∴;
结论运用:连接,延长、交于点,
∵,,
∴,
∵,,
∴符合探索延伸中的条件
∴结论成立,
即(海里),
答:此时两舰艇之间的距离是210海里.
期末复习解答题专题提升训练(附答案)
1.已知三角形的两个角分别是和,这两角所夹的边等于,如图所示,求作,使,,.(不写作法,保留作图痕迹)
2.如图,已知中,,.
(1)尺规作图:作的角平分线,交于点D(不写作法,保留作图痕迹).
(2)求的度数.
3.如图,相交于点O,,,连接,求证:.
4.如图,点C、E、B、F在一条直线上,于B,于E,,,求证:.
5.如图,在中,D为的中点.
(1)求证:;
(2)若,,求的取值范围.
6.已知,如图,在中,,,直线交于F,交于E,交的延长线于D,且,连接、,则与之间有何关系?请证明你的结论.
7.如图,在中,平分,于点E,点F在上,.
(1)求证:.
(2)若,求的长.
8.如图,已知,点分别在上,,.
(1)求证:;
(2)求证:.
9.如图,某校八年级(3)班的学生为了测量学校一幢教学楼的高度,在旗杆与楼之间选定一点P.用测角仪测得旗杆顶C视线与地面夹角,测楼顶A视线与地面夹角,量得P到楼底的距离与旗杆高度相等,等于10米,量得旗杆与楼之间距离为米,这样就可以计算出楼高了,楼高是多少米?
10.在中,,平分,M为直线上一动点,,E为垂足,的平分线交直线于点F.
(1)如图1,点M为边上一点,则的位置关系是___________,并证明;
(2)如图2,点M为边延长线上一点,则的位置关系是___________,并证明;
11.如图,中,,,是上一点,交的延长线于,于.
(1)求证:;
(2)若,,直接写出的长度.
12.如图,已知,,,当不动,绕点旋转时,连接,交于点,试判断与的位置关系与数量关系,并证明你的结论.
13.已知,如图,在中,,在中,,且,连接BD,CE交于点,连接.
(1)求证:;
(2)求证:.
14.如图,和的角平分线,相交点,.
(1)直接写出= °;
(2)求证:;
(3)若,求证:.
15.三条边都不相等的的和的平分线,相交于点.
(1)求证:;
(2)若,求的度数.
16.已知是的平分线,点P是射线上一定点,点C、D分别在射线、上,连接、.
(1)如图①,当,时,则与的数量关系是___________;
(2)如图②,点C、D在射线、上滑动,且,当时,与在(1)中的数量关系还成立吗?请说明理由.
(3)在问题(2)中,若,则四边形的面积S是否为定值?若是,请求出该定值,若不是,请说明理由.
17.在学习全等三角形的知识时,数学兴趣小组拿了两个大小不同的等腰直角三角板进行拼摆,并探究摆放后所构成的图形之间的关系,如图1,在和中,.
(1)勤奋小组摆出如图2所示的图形,点A和点D重合,连接和,求证:.
(2)超越小组在勤奋小组的启发下,把两个三角形板按如图3的方式摆放,点B,C,E在同一直线上,连接,他们发现了和之间的数量和位置关系,请写出这些关系,并说明理由.
18.如图1,在中,,点是直线上一点不与点、重合,以为一边在的右侧作,使,连接.设,.
(1)当点在线段上运动时,
①当时,则是多少?
②猜想与之间的数量关系,并对你的结论进行证明;
(2)如图2,当点在线段的反向延长线上运动时,猜想与之间的数量关系,并对你的结论给出证明.
(3)根据以往学习经验,点还可能在什么位置?请画出图形,直接写出与之间的数量关系.
19.问题背景:
(1)如图1,已知中,,,直线m经过点A,⊥直线m,⊥直线m,垂足分别为点D、E.求证:.
拓展延伸:
(2)如图2,将(1)中的条件改为:在中,,D、A、E三点都在直线m上,并且有.请写出、、三条线段的数量关系,并证明.
实际应用:
(3)如图3,在中,,,点C的坐标为,点A的坐标为,请直接写出B点的坐标.
20.【问题背景】
在四边形中,,,,、分别是、上的点,且,试探究图1中线段、、之间的数量关系.
【初步探索】
小亮同学认为:延长到点,使,连接,先证明,再证明,则可得到、、之间的数量关系是 ________________ .
【探索延伸】
在四边形中如图2,,,、分别是、上的点,,上述结论是否仍然成立?说明理由.
【结论运用】
如图3,在某次军事演习中,舰艇甲在指挥中心(处)北偏西的处,舰艇乙在指挥中心南偏东的处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以60海里/小时的速度前进,舰艇乙沿北偏东的方向以80海里/小时的速度前进1.5小时后,指挥中心观测到甲、乙两舰艇分别到达、处,且两舰艇之间的夹角()为,试求此时两舰艇之间的距离.
参考答案:
1.解:如图所示,即为所求.
2.解:(1)作图如图所示
(2)∵AD是的角平分线,
∴,
由三角形的外角等于与它不相邻的两个内角的和,
得,
∴.
3.证明:在和中,
,
∴.
∴.
4.证明:∵,,
∴,
在和中,
,
∴,
∴,
∴,
即:.
5.(1)证明:延长至点E,使,连接,
∵D为的中点,
∴,
又∵,,
∴,
∴,
∵,
∴.
(2)解:∵,
∵,
∴,
∴,
∵,,
∴,
∴.
6.解:,
理由如下:如图,∵,∴,
∴在与中,
∴(SAS),
∴,
延长交于点,
∵,∴,∴
∴.
7.(1)证明:∵平分,于点E,
∴.
在与中,
,
∴,
∴.
(2)解:设,则,
∵平分,于点E,
∴.
在与中,
,
∴,
∴,即,
解得,即.
8.(1)解: 证明:在和中,
∴ .
(2)解:由(1)知,
∴ ,
在和中,
∴ ,
∴.
9.解:∵,
,
,
∴,
在和中,
∵,
∴,
∴,
∵,
,
∴,
答:楼高是26米.
10.解:(1),理由如下:
过点作,
,,,
,
,
,
,
,
,
;
(2),理由如下:
延长交于点,
,,
,
.
,
,
.
11.(1)证明:.
.
,.
.
.
.
同角的余角相等,
在和中,
,
∴;
(2)∵,
,,
.
12.解:,,证明如下:
,
,即,
在和中,,
,
,,
又,
,
,即,
,
.
13.(1)解:证明:,
,
即,
在和中,
,
;
(2)如图,作于,作于.
由,
,,
,
,
点在平分线上,
平分,即.
14.解:(1),分别平分和,
,,
.
故答案为:120;
(2)过作,,,
,分别平分和,
,,
,
,,
,
,
,
,
在和中,
,
,
;
(3)如图,作的平分线交于点,则,
,,
,,
,,
,,
,
,,
,
,
在和中,
,
,
.
15.(1)证明:,分别是和的平分线,
,
,即,
.
(2)解:如图,过点作于点,作于点,连接,
则,
三条边都不相等的的和的平分线,相交于点,
是的角平分线,
,
在和中,,
,
,
,
由对顶角相等和(1)可知,,
,
又,
,
解得.
16.(1)解:∵是的平分线,
∴,
∵,,
∴,
在和中,
,
∴,
∴,
故答案为:.
(2)成立,理由如下:
过点P作于点E,于点F,
∵是的平分线,
∴,
∵,,
∴,
在和中,
,
∴,
∴,
∵,,,
∴,则,
∵,
∴,
∴,
在和中,
,
∴,
∴,
(3)由(2)可得:,
∴,
∵,
∴,
∵,
∴,
∵.
∴四边形的面积S为定值9.
17.(1)证明:∵,
∴,,
∴.
在和中,,
∴,
∴.
(2).理由如下:
∵,
∴,
∴,
在和中,
∴,
∴.
∵,
∴,
∴,
∴.
18.(1)解:①,
在与中,
又
四边形的内角和为
.
∵,
∴ .
② .
理由如下:
,
在与中,
又
四边形的内角和为
.
(2).
理由如下:
,,
在与中,
≌
,,
即 .
(3)点可能在的延长线上,图形如下,此时.
理由如下:
,,
在与中,
≌
,,
即 .
19.(1)证明:∵⊥直线m,直线m,
∴.
∵,
∴,
∵,
∴.
∵在和中,
,
∴≌,
∴,,
∴,
即:.
(2)解:数量关系.
理由如下:
在中,,
∵,,
∴,
在和中,
,
∴≌,
∴,,
∴;
(3)如图,作轴于E,轴于F,由(1)可知,≌,
,
∴,,
∴,
∴点B的坐标为.
20.解:初步探索:,
在和中,
,
∴,
∴,,
∵,,
∴,
∴,
∴,
在和中,
,
∴,
∴,
∴;
故答案为:,
探索延伸:结论仍然成立,
证明:延长到,使,连接,
∵,,
∴,
在和中,
,
∴,
∴,,
∵,
∴,
∴,
在和中,
,
∴,
∴,
∴;
结论运用:连接,延长、交于点,
∵,,
∴,
∵,,
∴符合探索延伸中的条件
∴结论成立,
即(海里),
答:此时两舰艇之间的距离是210海里.
