2023-2024学年华东师大版九年级上册数学期末复习试卷(无答案)
文档属性
| 名称 | 2023-2024学年华东师大版九年级上册数学期末复习试卷(无答案) | 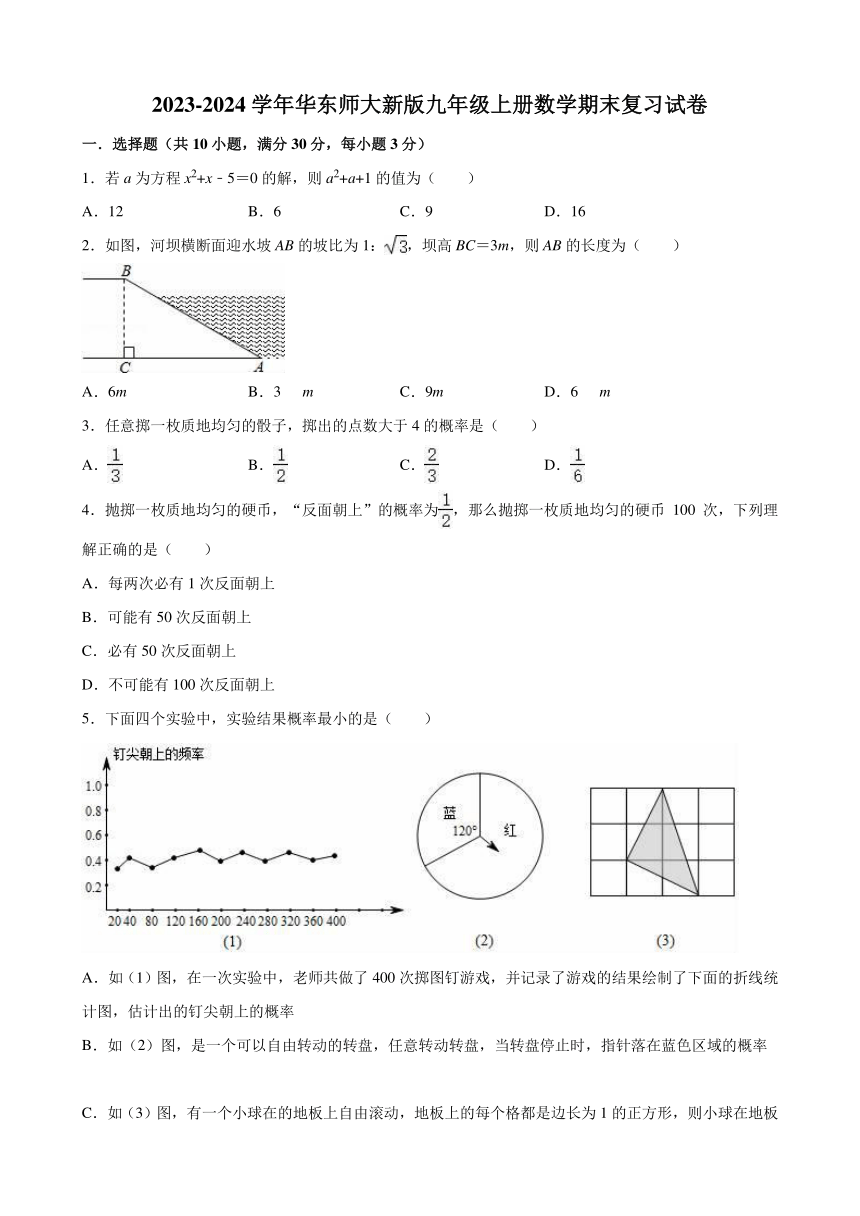 | |
| 格式 | docx | ||
| 文件大小 | 190.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-17 12:42:32 | ||
图片预览


文档简介
2023-2024学年华东师大新版九年级上册数学期末复习试卷
一.选择题(共10小题,满分30分,每小题3分)
1.若a为方程x2+x﹣5=0的解,则a2+a+1的值为( )
A.12 B.6 C.9 D.16
2.如图,河坝横断面迎水坡AB的坡比为1:,坝高BC=3m,则AB的长度为( )
A.6m B.3m C.9m D.6m
3.任意掷一枚质地均匀的骰子,掷出的点数大于4的概率是( )
A. B. C. D.
4.抛掷一枚质地均匀的硬币,“反面朝上”的概率为,那么抛掷一枚质地均匀的硬币100次,下列理解正确的是( )
A.每两次必有1次反面朝上
B.可能有50次反面朝上
C.必有50次反面朝上
D.不可能有100次反面朝上
5.下面四个实验中,实验结果概率最小的是( )
A.如(1)图,在一次实验中,老师共做了400次掷图钉游戏,并记录了游戏的结果绘制了下面的折线统计图,估计出的钉尖朝上的概率
B.如(2)图,是一个可以自由转动的转盘,任意转动转盘,当转盘停止时,指针落在蓝色区域的概率
C.如(3)图,有一个小球在的地板上自由滚动,地板上的每个格都是边长为1的正方形,则小球在地板上最终停留在黑色区域的概率
D.有7张卡片,分别标有数字1,2,3;4,6,8,9;将它们背面朝上洗匀后,从中随机抽出一张,抽出标有数字“大于6”的卡片的概率
6.已知关于x的一元二次方程(a﹣1)x2+2(a+2b)x+4b+2=0根的情况是( )
A.有两个不相等的实数根 B.有两个相等的实数根
C.没有实数根 D.以上都可能
7.在Rt△ABC中,∠C=90°,BC=5,AC=12,则sinB的值是( )
A. B. C. D.
8.今年,某中学响应习总书记“足球进校园”的号召,开设了“足球大课间”活动,现需要购进100个某品牌的足球供学生使用,经调查,该品牌足球2019年单价为200元,2021年单价为162元,2019年到2021年该品牌足球单价平均每年降低的百分率是( )
A.10% B.19% C.20% D.30%
9.从﹣3,0,1,2这四个数中任取一个数作为一元二次方程ax2+3x﹣1=0的系数a的值,能使该方程有实数根的概率是( )
A. B. C. D.
10.如图,等边△OAB的边OB在x轴上,点B坐标为(2,0),以点O为旋转中心,把△OAB逆时针旋转90°,则旋转后点A的对应点A'的坐标是( )
A.(﹣1,) B.(,﹣1) C.(﹣,1) D.(﹣2,1)
二.填空题(共5小题,满分15分,每小题3分)
1计算:的值为______.
2.在100张奖券中,其中5张有奖,某人从中任抽一张,则他中奖的概率是________.
3.如图,已知Rt△ABC中,∠C=90°,AC=3,BC=4,则sin B=________.
4.如图,河堤横断面的坡比是1∶,AC=12 m,则坡面AB的长度是________m.
5.如图,在边长是4×4,小正方形边长为1的正方形网格图中,线段AB的两个端点都在格点上,若以AB为斜边,则可以作出 个格点直角三角形,并在答题卡的图中作出其中面积最大的格点直角三角形.
三.解答题(共8小题,满分75分)
1.计算:2cos45°﹣|1﹣|+()﹣1﹣.
2我们发现,利用配方法解一元二次方程的步骤是相同的,因此,用配方法解一元二次方程ax2+bx+c=0(a≠0),可以得到一元二次方程的求根公式.一般地,对于一元二次方程ax2+bx+c=0(a≠0),当 时,它的根是: .用求根公式解一元二次方程的方法称为公式法.
(2)小明在用公式法解方程x2﹣5x=1时出现了错误,解答过程如下:
∵a=1,b=﹣5,c=1,(第一步)
∴b2﹣4ac=(﹣5)2﹣4×1×1=21.(第二步)
∴.(第三步)
∴.(第四步)
小明解答过程是从第 步开始出错的,其错误原因是 .
(3)请你写出此题正确的解答过程.
3.阅读以下内容,并回答问题:
定义:如果二次函数y=a1x2+b1x+c1(a1,b1,c1是常数,a1≠0)与y=a2x2+b2x+c2(a2,b2,c2是常数,a2≠0)满足a1+a2=0,b1=b2,c1+c2=0,则称这两个函数互为“旋转函数”.
(1)请写出函数y=﹣x2+4x﹣3的“旋转函数”的表达式及其顶点的坐标;
(2)已知函数y=﹣(x+2)(x﹣3)的图象与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,点A,B,C关于原点的对称点分别是A',B',C',试判断过点A',B',C′的二次函数与函数y=﹣(x+2)(x﹣3)是否互为“旋转函数”,并说明理由.
4.已知关于x的一元二次方程x2﹣5x+m=0.
(1)若方程有实数根,求实数m的取值范围;
(2)若方程两实数根为x1,x2,且满足3x1﹣2x2=5,求实数m的值.
5.空中缆车是旅游时上、下山和进行空中参观的交通工具.如图,小明一家去某著名风景区旅游,准备先从山脚A走台阶步行到B,再换乘缆车到山顶C.从A到B的路线可看作是坡角为30°的斜坡,长度为1 200米;从B到C的缆车路线可看作是直线,其与水平线的夹角为45°,且缆车从B到C的平均速度为6米/秒,运行时间为10分钟,求山顶C到AD的距离(结果保留根号).
6.请阅读下列材料,并完成相应的任务:
阿尔·花拉子米(约780~约850),著名数学家、天文学家、地理学家,是代数与算术的整理者,被誉为“代数之父”.他利用正方形图形巧妙解出了一元二次方程x2+2x-35=0的一个正根.将边长为x的正方形和边长为1的正方形,外加两个长方形,长为x,宽为1,拼合在一起面积就是x2+2x×1+12,即 x2+2x+1,而由原方程x2+2x-35=0变形得x2+2x+1=35+1,即边长为 x+1的正方形面积为36.所以(x+1)2=36,则x=5.
任务:
(1)上述求解过程中所用的方法与下列哪种方法是一致的( )
A.直接开平方法 B.公式法
C.配方法 D.因式分解法
(2)所用的数学思想方法是( )
A.分类讨论思想 B.数形结合思想
C.建模思想 D.整体思想
(3)运用上述方法构造出符合方程x2+6x-7=0的一个正根的正方形(画出拼接的正方形并求出正根).
7.如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,动点P在线段AB上以每秒3个单位的速度从点A运动到点B,过点P作PD⊥AB,交射线AC于点D,以PB、PD为邻边作矩形PDEB,设点P的运动时间为t s.
(1)求PD的长;(用含t的代数式来表示)
(2)当点D在∠ABC的平分线上时,求t的值;
(3)当BC平分矩形PDEB的某一边时,直接写出t的值.
8如图1,抛物线y=ax2+2x+c(a≠0)与x轴,y轴分别交于点A(﹣1,0),B点,C(0,3)三点.
(1)求抛物线的解析式;
(2)点D(m,3)在抛物线上,连接BC,BD.在对称轴左侧的抛物线上是否存在一点P,满足∠PBC=∠DBC?如果存在,请求出点P点的坐标;如果不存在,请说明理由;
(3)点N在抛物线的对称轴上,点M在抛物线上,当以M、N、B、C为顶点的四边形是平行四边形时,请直接写出点M的坐标.
一.选择题(共10小题,满分30分,每小题3分)
1.若a为方程x2+x﹣5=0的解,则a2+a+1的值为( )
A.12 B.6 C.9 D.16
2.如图,河坝横断面迎水坡AB的坡比为1:,坝高BC=3m,则AB的长度为( )
A.6m B.3m C.9m D.6m
3.任意掷一枚质地均匀的骰子,掷出的点数大于4的概率是( )
A. B. C. D.
4.抛掷一枚质地均匀的硬币,“反面朝上”的概率为,那么抛掷一枚质地均匀的硬币100次,下列理解正确的是( )
A.每两次必有1次反面朝上
B.可能有50次反面朝上
C.必有50次反面朝上
D.不可能有100次反面朝上
5.下面四个实验中,实验结果概率最小的是( )
A.如(1)图,在一次实验中,老师共做了400次掷图钉游戏,并记录了游戏的结果绘制了下面的折线统计图,估计出的钉尖朝上的概率
B.如(2)图,是一个可以自由转动的转盘,任意转动转盘,当转盘停止时,指针落在蓝色区域的概率
C.如(3)图,有一个小球在的地板上自由滚动,地板上的每个格都是边长为1的正方形,则小球在地板上最终停留在黑色区域的概率
D.有7张卡片,分别标有数字1,2,3;4,6,8,9;将它们背面朝上洗匀后,从中随机抽出一张,抽出标有数字“大于6”的卡片的概率
6.已知关于x的一元二次方程(a﹣1)x2+2(a+2b)x+4b+2=0根的情况是( )
A.有两个不相等的实数根 B.有两个相等的实数根
C.没有实数根 D.以上都可能
7.在Rt△ABC中,∠C=90°,BC=5,AC=12,则sinB的值是( )
A. B. C. D.
8.今年,某中学响应习总书记“足球进校园”的号召,开设了“足球大课间”活动,现需要购进100个某品牌的足球供学生使用,经调查,该品牌足球2019年单价为200元,2021年单价为162元,2019年到2021年该品牌足球单价平均每年降低的百分率是( )
A.10% B.19% C.20% D.30%
9.从﹣3,0,1,2这四个数中任取一个数作为一元二次方程ax2+3x﹣1=0的系数a的值,能使该方程有实数根的概率是( )
A. B. C. D.
10.如图,等边△OAB的边OB在x轴上,点B坐标为(2,0),以点O为旋转中心,把△OAB逆时针旋转90°,则旋转后点A的对应点A'的坐标是( )
A.(﹣1,) B.(,﹣1) C.(﹣,1) D.(﹣2,1)
二.填空题(共5小题,满分15分,每小题3分)
1计算:的值为______.
2.在100张奖券中,其中5张有奖,某人从中任抽一张,则他中奖的概率是________.
3.如图,已知Rt△ABC中,∠C=90°,AC=3,BC=4,则sin B=________.
4.如图,河堤横断面的坡比是1∶,AC=12 m,则坡面AB的长度是________m.
5.如图,在边长是4×4,小正方形边长为1的正方形网格图中,线段AB的两个端点都在格点上,若以AB为斜边,则可以作出 个格点直角三角形,并在答题卡的图中作出其中面积最大的格点直角三角形.
三.解答题(共8小题,满分75分)
1.计算:2cos45°﹣|1﹣|+()﹣1﹣.
2我们发现,利用配方法解一元二次方程的步骤是相同的,因此,用配方法解一元二次方程ax2+bx+c=0(a≠0),可以得到一元二次方程的求根公式.一般地,对于一元二次方程ax2+bx+c=0(a≠0),当 时,它的根是: .用求根公式解一元二次方程的方法称为公式法.
(2)小明在用公式法解方程x2﹣5x=1时出现了错误,解答过程如下:
∵a=1,b=﹣5,c=1,(第一步)
∴b2﹣4ac=(﹣5)2﹣4×1×1=21.(第二步)
∴.(第三步)
∴.(第四步)
小明解答过程是从第 步开始出错的,其错误原因是 .
(3)请你写出此题正确的解答过程.
3.阅读以下内容,并回答问题:
定义:如果二次函数y=a1x2+b1x+c1(a1,b1,c1是常数,a1≠0)与y=a2x2+b2x+c2(a2,b2,c2是常数,a2≠0)满足a1+a2=0,b1=b2,c1+c2=0,则称这两个函数互为“旋转函数”.
(1)请写出函数y=﹣x2+4x﹣3的“旋转函数”的表达式及其顶点的坐标;
(2)已知函数y=﹣(x+2)(x﹣3)的图象与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,点A,B,C关于原点的对称点分别是A',B',C',试判断过点A',B',C′的二次函数与函数y=﹣(x+2)(x﹣3)是否互为“旋转函数”,并说明理由.
4.已知关于x的一元二次方程x2﹣5x+m=0.
(1)若方程有实数根,求实数m的取值范围;
(2)若方程两实数根为x1,x2,且满足3x1﹣2x2=5,求实数m的值.
5.空中缆车是旅游时上、下山和进行空中参观的交通工具.如图,小明一家去某著名风景区旅游,准备先从山脚A走台阶步行到B,再换乘缆车到山顶C.从A到B的路线可看作是坡角为30°的斜坡,长度为1 200米;从B到C的缆车路线可看作是直线,其与水平线的夹角为45°,且缆车从B到C的平均速度为6米/秒,运行时间为10分钟,求山顶C到AD的距离(结果保留根号).
6.请阅读下列材料,并完成相应的任务:
阿尔·花拉子米(约780~约850),著名数学家、天文学家、地理学家,是代数与算术的整理者,被誉为“代数之父”.他利用正方形图形巧妙解出了一元二次方程x2+2x-35=0的一个正根.将边长为x的正方形和边长为1的正方形,外加两个长方形,长为x,宽为1,拼合在一起面积就是x2+2x×1+12,即 x2+2x+1,而由原方程x2+2x-35=0变形得x2+2x+1=35+1,即边长为 x+1的正方形面积为36.所以(x+1)2=36,则x=5.
任务:
(1)上述求解过程中所用的方法与下列哪种方法是一致的( )
A.直接开平方法 B.公式法
C.配方法 D.因式分解法
(2)所用的数学思想方法是( )
A.分类讨论思想 B.数形结合思想
C.建模思想 D.整体思想
(3)运用上述方法构造出符合方程x2+6x-7=0的一个正根的正方形(画出拼接的正方形并求出正根).
7.如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,动点P在线段AB上以每秒3个单位的速度从点A运动到点B,过点P作PD⊥AB,交射线AC于点D,以PB、PD为邻边作矩形PDEB,设点P的运动时间为t s.
(1)求PD的长;(用含t的代数式来表示)
(2)当点D在∠ABC的平分线上时,求t的值;
(3)当BC平分矩形PDEB的某一边时,直接写出t的值.
8如图1,抛物线y=ax2+2x+c(a≠0)与x轴,y轴分别交于点A(﹣1,0),B点,C(0,3)三点.
(1)求抛物线的解析式;
(2)点D(m,3)在抛物线上,连接BC,BD.在对称轴左侧的抛物线上是否存在一点P,满足∠PBC=∠DBC?如果存在,请求出点P点的坐标;如果不存在,请说明理由;
(3)点N在抛物线的对称轴上,点M在抛物线上,当以M、N、B、C为顶点的四边形是平行四边形时,请直接写出点M的坐标.
同课章节目录
