20.2.1中位数和众数 课件
图片预览





文档简介
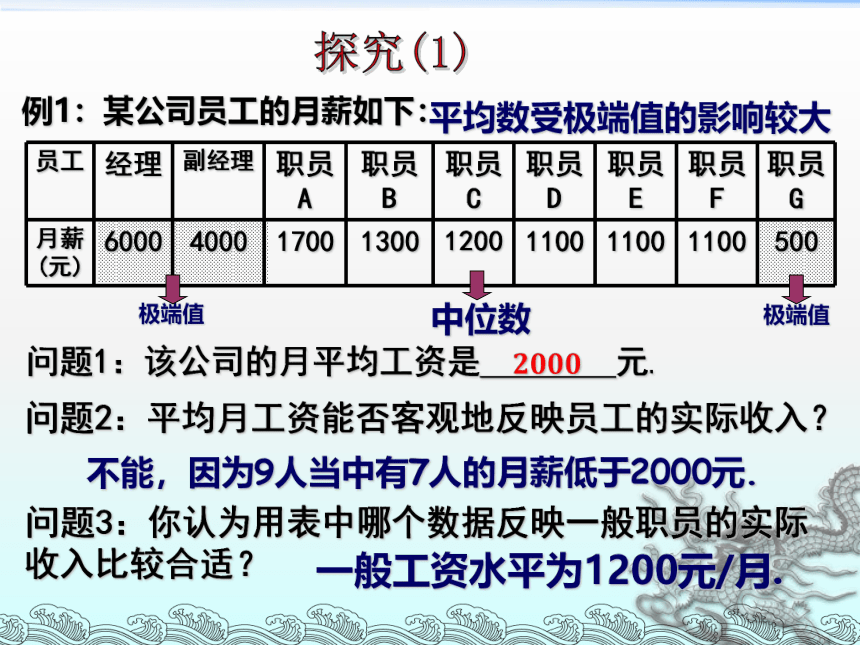
课件17张PPT。20.1.2数据的代表中位数和众数例1:某公司员工的月薪如下:问题1:该公司的月平均工资是 元.问题2:平均月工资能否客观地反映员工的实际收入?问题3:你认为用表中哪个数据反映一般职员的实际收入比较合适?探究(1)2000中位数一般工资水平为1200元/月.极端值极端值不能,因为9人当中有7人的月薪低于2000元.平均数受极端值的影响较大你能求出下列各组数据的中位数吗?(1)1、2、3
(2)2、3、5、6、7、
(3)21、23、24、25、27、28、39
(4)1、2、3、4
(5)2、3、5、6、7、9
(6)21、23、24、25、27、28、39、40
想一想2.55.526一组数据按大小顺序排列之后,最中间的那个数或最中间两个数的平均数叫做这组数据的中位数.1、中位数定义注:(1)中位数仅与数据的排列位置有关,当一组数据中的个别数据变动较大时,可用它来描述其集中趋势.
(2)中位数要写单位你能求出下列各组数据的中位数吗?(1)1、2、3
(2)2、3、5、6、7、
(3)21、23、24、25、27、28、39
(4)1、2、3、4
(5)2、3、5、6、7、9
(6)21、23、24、25、27、28、39、40
2.55.526.52、如何找出中位数你发现什么规律了吗? n个数据按大小顺序排列之后,
(1)若n为奇数,则第 个为中位数;
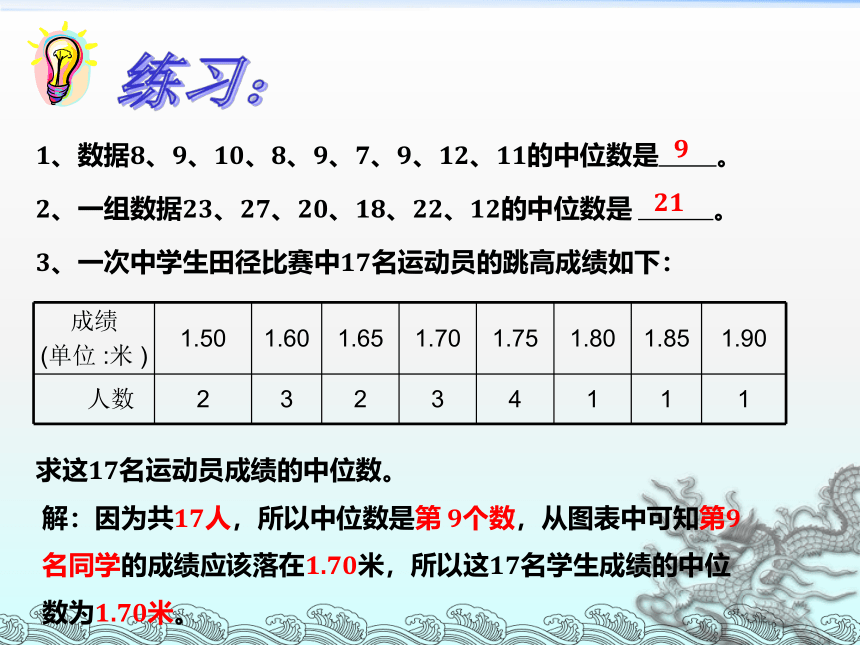
(2)若n为偶数,则第 __ 个、第 __ 个的平均数为中位数.2、如何找出中位数注:中位数是一个位置代表值.在一组数据中,中位数位于数据的最中间位置,小于等于和大于等于中位数的数据一样多.1、数据8、9、10、8、9、7、9、12、11的中位数是 。
2、一组数据23、27、20、18、22、12的中位数是 。
3、一次中学生田径比赛中17名运动员的跳高成绩如下:
求这17名运动员成绩的中位数。
921解:因为共17人,所以中位数是第 9个数,从图表中可知第9名同学的成绩应该落在1.70米,所以这17名学生成绩的中位数为1.70米。练习:变式:在一次马拉松长跑比赛中,抽得12名选手所用时间如下(单位:分):
136 140 129 180 124 154
146 145 158 175 165 148 (1)样本数据(12名选手所用时间)的中位数是多少?(2)一名选手的成绩是142分,他的成绩如何?(2)因为142<147,所以他的成绩处于中上水平.解:(1)将这组数据按照从小到大的顺序排列为:124,129,136,140, 145,146,148,154,158,165,175,180所以中位数为:分速算题3、10名工人某天生产同一零件,生产的件数是:
15 17 14 10 15
19 17 16 14 12
求这一天10名工人生产的零件的中位数. 1、在一次数学竞赛中,5名学生的成绩分别是(单位:分)98,55,62,57,61,那么它们的中位数是 _______. 2、在数据-1,0,4,5,8中插入一个数据x,使得这组数据的中位数是3,则x= .解:先将这组数据按照由小到大的顺序排列:
10,12,14 ,14,15,15,16,17,17 ,19处于中间的两个数是15与15,则中位数是 61分2例1:某公司员工的月薪如下:探究(2)中位数极端值极端值平均数受极端值的影响较大众数2、众数定义一组数据中,出现次数最多的那个数据叫做这组数据的众数.注:(1)众数要写单位。1.你能找出下列各组数据中的众数吗? (1)2、21、5、5、2、4、2
(2)3、1、5、4、2、1、1、3
2.你认为这两组数据中的众数是多少呢?
(1)1、2、2、3、3、-5
(2)5、6、6、5、13.你认为下面这两组数据有没有众数,为什么?
(1)1、2、3、4、5、6、7、8
(2)1、1、2、2、3、3、4、4练习:注:(2)一组数据中的众数有时不止一个,当有两个或者两个以上数据出现次数都是最多时,它们都是这组数据的众数。(3)当一组数据中各个数字出现的次数都相同时,这组数据没有众数。212和35和6没有没有例2、一家鞋店在一段时间内销售了某种运动鞋30双,各种尺码的鞋的销售量如下:假如你是老板,你最关心哪一个统计量?你会如何进货?解:最关心是众数,尺码为23.5cm的鞋多进一些.练习:一组数据8,8,x,6的众数与平均数相同,那么
x= ,这数据的中位数是 .108试一试你的身手1.数据8, 2, 7, 9 , 2, 7, 2, 的众数是____ ,中位数是____.2.数据20, 20, 15, 22,30,30的众数是___________ ,中位数是______ 3.在数据-1, 0, 4, 5, 8中插入一个数据x ,使得这组数据的中位数是3,则x=_____ 4.数据8, 8, x, 6的众数与平均数相同,那么它们的中位数是____ 5.(中考链接)5个正整数从小到大排列,若这组数据的中位 数是3,唯一的众数是7,则这5个正整数的和是( )
A.20 B.21 C.22 D.23 2720和302128A6.双语学校第二届校运会初二的男子跳高比赛中,12名选手的成绩如下(单位:cm):
115 120 128 130 123 110
105 125 125 127 132 120处于中间的两个数是123与125,则中位数是
众数有两个,是120和125 这组数据的中位数是多少?众数是多少?解:先将这组数据按照由小到大的顺序排列:
105 110 115 120 120 123
125 125 127 128 130 1327.为了解开展“孝敬父母,从家务事做起”活动的实施情况,某校抽取八年级某班50名学生,调查他们一周做家务所用时间,得到一组数据,并绘制成下表,请根据下表完成各题:(1)填写图中未完成的部分;8 (3)这组数据的中位数是 ________ ,众数是 _____ . 2.5小时3小时(2)该班学生每周做家务的平均时间是 _________ .2.44小时如何求一组数据的中位数,众数?应注意什么? 1.求中位数要将一组数据按大小顺序,顾名思义,中位数就是位置处于最中间的一个数(或最中间的两个数的平均数),排序时,从小到大或从大到小都可以.2.众数是一组数据中出现次数最多的数据,是一组数据中的原数据,而不是相应的次数.众数有可能不唯一,注意不要遗漏. 小结1.平均数的计算要用到所有的数据,它能够充
分利用数据提供的信息,在现实生活中较为常
用.但它受极端值的影响较大.3.当一组数据中某些数据多次重复出现时,众数往往是人们关心的一个量,众数不受极端值的影响,这是它的一个优势.2.中位数只需很少的计算,不受极端值的影响,当一组数据中的个别数据变动较大时,可用它来描述其集中趋势.归纳
(2)2、3、5、6、7、
(3)21、23、24、25、27、28、39
(4)1、2、3、4
(5)2、3、5、6、7、9
(6)21、23、24、25、27、28、39、40
想一想2.55.526一组数据按大小顺序排列之后,最中间的那个数或最中间两个数的平均数叫做这组数据的中位数.1、中位数定义注:(1)中位数仅与数据的排列位置有关,当一组数据中的个别数据变动较大时,可用它来描述其集中趋势.
(2)中位数要写单位你能求出下列各组数据的中位数吗?(1)1、2、3
(2)2、3、5、6、7、
(3)21、23、24、25、27、28、39
(4)1、2、3、4
(5)2、3、5、6、7、9
(6)21、23、24、25、27、28、39、40
2.55.526.52、如何找出中位数你发现什么规律了吗? n个数据按大小顺序排列之后,
(1)若n为奇数,则第 个为中位数;
(2)若n为偶数,则第 __ 个、第 __ 个的平均数为中位数.2、如何找出中位数注:中位数是一个位置代表值.在一组数据中,中位数位于数据的最中间位置,小于等于和大于等于中位数的数据一样多.1、数据8、9、10、8、9、7、9、12、11的中位数是 。
2、一组数据23、27、20、18、22、12的中位数是 。
3、一次中学生田径比赛中17名运动员的跳高成绩如下:
求这17名运动员成绩的中位数。
921解:因为共17人,所以中位数是第 9个数,从图表中可知第9名同学的成绩应该落在1.70米,所以这17名学生成绩的中位数为1.70米。练习:变式:在一次马拉松长跑比赛中,抽得12名选手所用时间如下(单位:分):
136 140 129 180 124 154
146 145 158 175 165 148 (1)样本数据(12名选手所用时间)的中位数是多少?(2)一名选手的成绩是142分,他的成绩如何?(2)因为142<147,所以他的成绩处于中上水平.解:(1)将这组数据按照从小到大的顺序排列为:124,129,136,140, 145,146,148,154,158,165,175,180所以中位数为:分速算题3、10名工人某天生产同一零件,生产的件数是:
15 17 14 10 15
19 17 16 14 12
求这一天10名工人生产的零件的中位数. 1、在一次数学竞赛中,5名学生的成绩分别是(单位:分)98,55,62,57,61,那么它们的中位数是 _______. 2、在数据-1,0,4,5,8中插入一个数据x,使得这组数据的中位数是3,则x= .解:先将这组数据按照由小到大的顺序排列:
10,12,14 ,14,15,15,16,17,17 ,19处于中间的两个数是15与15,则中位数是 61分2例1:某公司员工的月薪如下:探究(2)中位数极端值极端值平均数受极端值的影响较大众数2、众数定义一组数据中,出现次数最多的那个数据叫做这组数据的众数.注:(1)众数要写单位。1.你能找出下列各组数据中的众数吗? (1)2、21、5、5、2、4、2
(2)3、1、5、4、2、1、1、3
2.你认为这两组数据中的众数是多少呢?
(1)1、2、2、3、3、-5
(2)5、6、6、5、13.你认为下面这两组数据有没有众数,为什么?
(1)1、2、3、4、5、6、7、8
(2)1、1、2、2、3、3、4、4练习:注:(2)一组数据中的众数有时不止一个,当有两个或者两个以上数据出现次数都是最多时,它们都是这组数据的众数。(3)当一组数据中各个数字出现的次数都相同时,这组数据没有众数。212和35和6没有没有例2、一家鞋店在一段时间内销售了某种运动鞋30双,各种尺码的鞋的销售量如下:假如你是老板,你最关心哪一个统计量?你会如何进货?解:最关心是众数,尺码为23.5cm的鞋多进一些.练习:一组数据8,8,x,6的众数与平均数相同,那么
x= ,这数据的中位数是 .108试一试你的身手1.数据8, 2, 7, 9 , 2, 7, 2, 的众数是____ ,中位数是____.2.数据20, 20, 15, 22,30,30的众数是___________ ,中位数是______ 3.在数据-1, 0, 4, 5, 8中插入一个数据x ,使得这组数据的中位数是3,则x=_____ 4.数据8, 8, x, 6的众数与平均数相同,那么它们的中位数是____ 5.(中考链接)5个正整数从小到大排列,若这组数据的中位 数是3,唯一的众数是7,则这5个正整数的和是( )
A.20 B.21 C.22 D.23 2720和302128A6.双语学校第二届校运会初二的男子跳高比赛中,12名选手的成绩如下(单位:cm):
115 120 128 130 123 110
105 125 125 127 132 120处于中间的两个数是123与125,则中位数是
众数有两个,是120和125 这组数据的中位数是多少?众数是多少?解:先将这组数据按照由小到大的顺序排列:
105 110 115 120 120 123
125 125 127 128 130 1327.为了解开展“孝敬父母,从家务事做起”活动的实施情况,某校抽取八年级某班50名学生,调查他们一周做家务所用时间,得到一组数据,并绘制成下表,请根据下表完成各题:(1)填写图中未完成的部分;8 (3)这组数据的中位数是 ________ ,众数是 _____ . 2.5小时3小时(2)该班学生每周做家务的平均时间是 _________ .2.44小时如何求一组数据的中位数,众数?应注意什么? 1.求中位数要将一组数据按大小顺序,顾名思义,中位数就是位置处于最中间的一个数(或最中间的两个数的平均数),排序时,从小到大或从大到小都可以.2.众数是一组数据中出现次数最多的数据,是一组数据中的原数据,而不是相应的次数.众数有可能不唯一,注意不要遗漏. 小结1.平均数的计算要用到所有的数据,它能够充
分利用数据提供的信息,在现实生活中较为常
用.但它受极端值的影响较大.3.当一组数据中某些数据多次重复出现时,众数往往是人们关心的一个量,众数不受极端值的影响,这是它的一个优势.2.中位数只需很少的计算,不受极端值的影响,当一组数据中的个别数据变动较大时,可用它来描述其集中趋势.归纳
