六年级下册数学人教版3.2 圆柱的表面积课件(共18张PPT)
文档属性
| 名称 | 六年级下册数学人教版3.2 圆柱的表面积课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 424.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-16 00:00:00 | ||
图片预览





文档简介
(共18张PPT)
圆柱的表面积
目录
01
圆柱的表面积公式
02
圆柱的表面积计算
03
圆柱的表面积应用
04
圆柱的表面积与圆锥的表面积比较
圆柱的表面积公式
2
圆柱的表面积公式推导
圆柱的表面积包括侧面积和两个底面积
侧面积的计算方法是将圆柱的侧面展开,得到一个长方形,长方形的长是圆柱的底面周长,宽是圆柱的高
底面积的计算方法是将圆柱的底面看作一个圆形,半径是圆柱的底面半径,面积是πr
综合以上推导,得到圆柱的表面积公式为:2πr + 2πrh
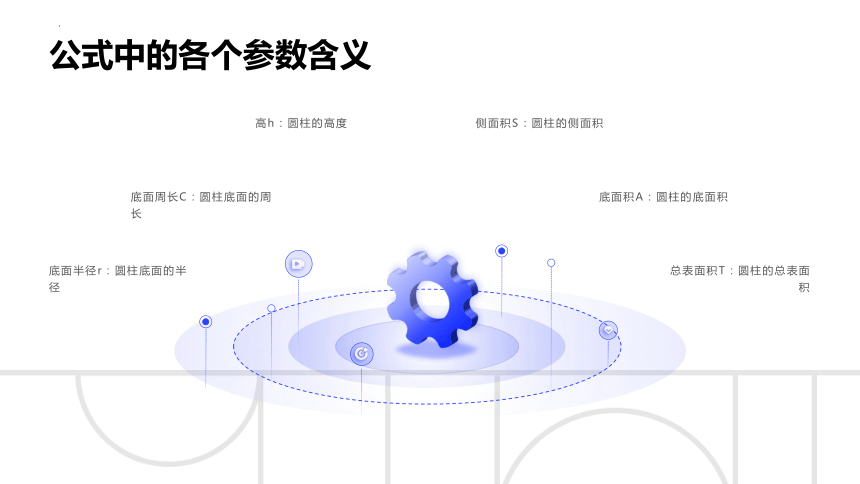
公式中的各个参数含义
底面半径r:圆柱底面的半径
总表面积T:圆柱的总表面积
底面积A:圆柱的底面积
底面周长C:圆柱底面的周长
侧面积S:圆柱的侧面积
高h:圆柱的高度
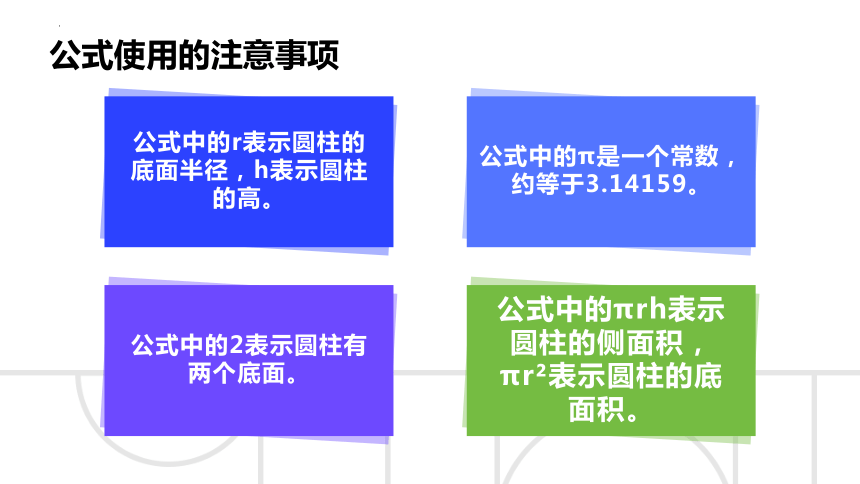
公式使用的注意事项
公式中的r表示圆柱的底面半径,h表示圆柱的高。
公式中的π是一个常数,约等于3.14159。
公式中的2表示圆柱有两个底面。
公式中的πrh表示圆柱的侧面积,πr 表示圆柱的底面积。
圆柱的表面积计算
3
计算侧面积
侧面积的应用:计算圆柱形物体的包装材料面积,或者计算圆柱形物体的表面积时,需要将侧面积计算在内
侧面积的计算方法:将圆柱的侧面展开,得到一个长方形,长方形的长为圆柱的底面周长,宽为圆柱的高度
其中,r为圆柱的半径,h为圆柱的高度
侧面积公式:2πrh
计算底面积
底面积公式:πr^2
注意事项:计算时确保单位统一,避免因单位换算错误导致结果错误
底面积计算示例:例如,一个圆柱底面半径为5cm,则底面积为π*5^2=25π平方厘米
r为底面半径
计算表面积的步骤和示例
确定圆柱的半径和高度
计算圆柱的底面积:πr^2
计算圆柱的侧面积:2πrh
计算圆柱的表面积:2πr^2 + 2πrh
示例:半径为5,高度为10的圆柱,表面积为2π(5^2) + 2π(5)(10) = 100π + 100π = 200π
圆柱的表面积应用
4
表面积在生活中的应用
包装设计:根据圆柱的表面积计算所需包装材料的面积
建筑设计:根据圆柱的表面积计算所需建筑材料的面积
管道设计:根据圆柱的表面积计算所需管道材料的面积
容器设计:根据圆柱的表面积计算所需容器材料的面积
表面积在数学问题中的应用
圆柱的表面积在物理问题中的应用:如计算圆柱形物体的转动惯量、流体力学中的阻力等
圆柱的表面积在数学问题中的应用:如计算圆柱体的侧面积、全面积等
圆柱的表面积在实际生活中的应用:如计算圆柱形物体的包装面积、体积等
圆柱的表面积公式:2πr(h+r)
表面积与其他几何形状的联系
圆柱的表面积:两个底面积和一个侧面积
圆锥的表面积:一个底面积和一个侧面积
球的表面积:4πr^2
棱柱的表面积:两个底面积和四个侧面积
棱锥的表面积:一个底面积和一个侧面积
圆台的表面积:一个底面积和一个侧面积
圆柱的表面积与圆锥的表面积比较
5
圆锥的表面积公式
圆锥的表面积由侧面积和底面积组成
侧面积公式:πrl
底面积公式:πr^2
其中,r为圆锥的半径,l为圆锥的母线长
圆柱与圆锥表面积的比较
圆柱的表面积:2πr(h+r)
圆锥的表面积:πr(r+l)
比较:圆柱的表面积是圆锥的表面积的2倍
结论:圆柱的表面积大于圆锥的表面积
表面积在几何学习中的重要性
添加标题
添加标题
添加标题
添加标题
计算体积和表面积
理解几何体的形状和结构
比较不同几何体的表面积
应用在实际生活和工程设计中
圆柱的表面积
目录
01
圆柱的表面积公式
02
圆柱的表面积计算
03
圆柱的表面积应用
04
圆柱的表面积与圆锥的表面积比较
圆柱的表面积公式
2
圆柱的表面积公式推导
圆柱的表面积包括侧面积和两个底面积
侧面积的计算方法是将圆柱的侧面展开,得到一个长方形,长方形的长是圆柱的底面周长,宽是圆柱的高
底面积的计算方法是将圆柱的底面看作一个圆形,半径是圆柱的底面半径,面积是πr
综合以上推导,得到圆柱的表面积公式为:2πr + 2πrh
公式中的各个参数含义
底面半径r:圆柱底面的半径
总表面积T:圆柱的总表面积
底面积A:圆柱的底面积
底面周长C:圆柱底面的周长
侧面积S:圆柱的侧面积
高h:圆柱的高度
公式使用的注意事项
公式中的r表示圆柱的底面半径,h表示圆柱的高。
公式中的π是一个常数,约等于3.14159。
公式中的2表示圆柱有两个底面。
公式中的πrh表示圆柱的侧面积,πr 表示圆柱的底面积。
圆柱的表面积计算
3
计算侧面积
侧面积的应用:计算圆柱形物体的包装材料面积,或者计算圆柱形物体的表面积时,需要将侧面积计算在内
侧面积的计算方法:将圆柱的侧面展开,得到一个长方形,长方形的长为圆柱的底面周长,宽为圆柱的高度
其中,r为圆柱的半径,h为圆柱的高度
侧面积公式:2πrh
计算底面积
底面积公式:πr^2
注意事项:计算时确保单位统一,避免因单位换算错误导致结果错误
底面积计算示例:例如,一个圆柱底面半径为5cm,则底面积为π*5^2=25π平方厘米
r为底面半径
计算表面积的步骤和示例
确定圆柱的半径和高度
计算圆柱的底面积:πr^2
计算圆柱的侧面积:2πrh
计算圆柱的表面积:2πr^2 + 2πrh
示例:半径为5,高度为10的圆柱,表面积为2π(5^2) + 2π(5)(10) = 100π + 100π = 200π
圆柱的表面积应用
4
表面积在生活中的应用
包装设计:根据圆柱的表面积计算所需包装材料的面积
建筑设计:根据圆柱的表面积计算所需建筑材料的面积
管道设计:根据圆柱的表面积计算所需管道材料的面积
容器设计:根据圆柱的表面积计算所需容器材料的面积
表面积在数学问题中的应用
圆柱的表面积在物理问题中的应用:如计算圆柱形物体的转动惯量、流体力学中的阻力等
圆柱的表面积在数学问题中的应用:如计算圆柱体的侧面积、全面积等
圆柱的表面积在实际生活中的应用:如计算圆柱形物体的包装面积、体积等
圆柱的表面积公式:2πr(h+r)
表面积与其他几何形状的联系
圆柱的表面积:两个底面积和一个侧面积
圆锥的表面积:一个底面积和一个侧面积
球的表面积:4πr^2
棱柱的表面积:两个底面积和四个侧面积
棱锥的表面积:一个底面积和一个侧面积
圆台的表面积:一个底面积和一个侧面积
圆柱的表面积与圆锥的表面积比较
5
圆锥的表面积公式
圆锥的表面积由侧面积和底面积组成
侧面积公式:πrl
底面积公式:πr^2
其中,r为圆锥的半径,l为圆锥的母线长
圆柱与圆锥表面积的比较
圆柱的表面积:2πr(h+r)
圆锥的表面积:πr(r+l)
比较:圆柱的表面积是圆锥的表面积的2倍
结论:圆柱的表面积大于圆锥的表面积
表面积在几何学习中的重要性
添加标题
添加标题
添加标题
添加标题
计算体积和表面积
理解几何体的形状和结构
比较不同几何体的表面积
应用在实际生活和工程设计中
