4.1 光的折射 讲义
图片预览



文档简介
1 光的折射
教学分析
学生在初中阶段已经接触过光的折射等知识,本节课属于人教版2019第四章第一节内容,教师要帮助学生在已有的知识基础上理解和掌握光的折射现象,要通过实验探究掌握实验方法,解决具体问题。
教学课时
2个课时
教学目标
(1)掌握折射定律,能光的折射定律解决相关问题。
(2)掌握介质的折射率的概念。
(3)经历根据实验原理设计测量玻璃的折射率的过程。
教学重难点
教学重点
折射定律、折射率、实验设计、实验操作、数据处理
教学难点
折射定律、折射率、实验设计、数据处理
教学准备
多媒体课件、木板、白纸、图钉、大头针、玻璃砖、铅笔、直尺、量角器。
教学过程
新课引入
教师设问:潭清疑水浅,荷动知鱼散。这是唐代诗人储光羲《钓鱼湾》中的诗句。为什么潭清疑水浅?这就是我们这节课要解决的问题。
讲授新课
一 折射定律
教师设问:请大家回顾一下初中所学的光的折射规律。
学生活动:小组内讨论光的折射规律。
教师活动:播放学生初中所学的探究光的折射规律的视频。
学生活动:观看老师播放的视频。
教师活动:口述学生初中所学的折射规律。
教师设问:折射角与入射角有没有定量的关系呢?
学生活动:思考老师所提问题。
教师活动:讲解折射定律。
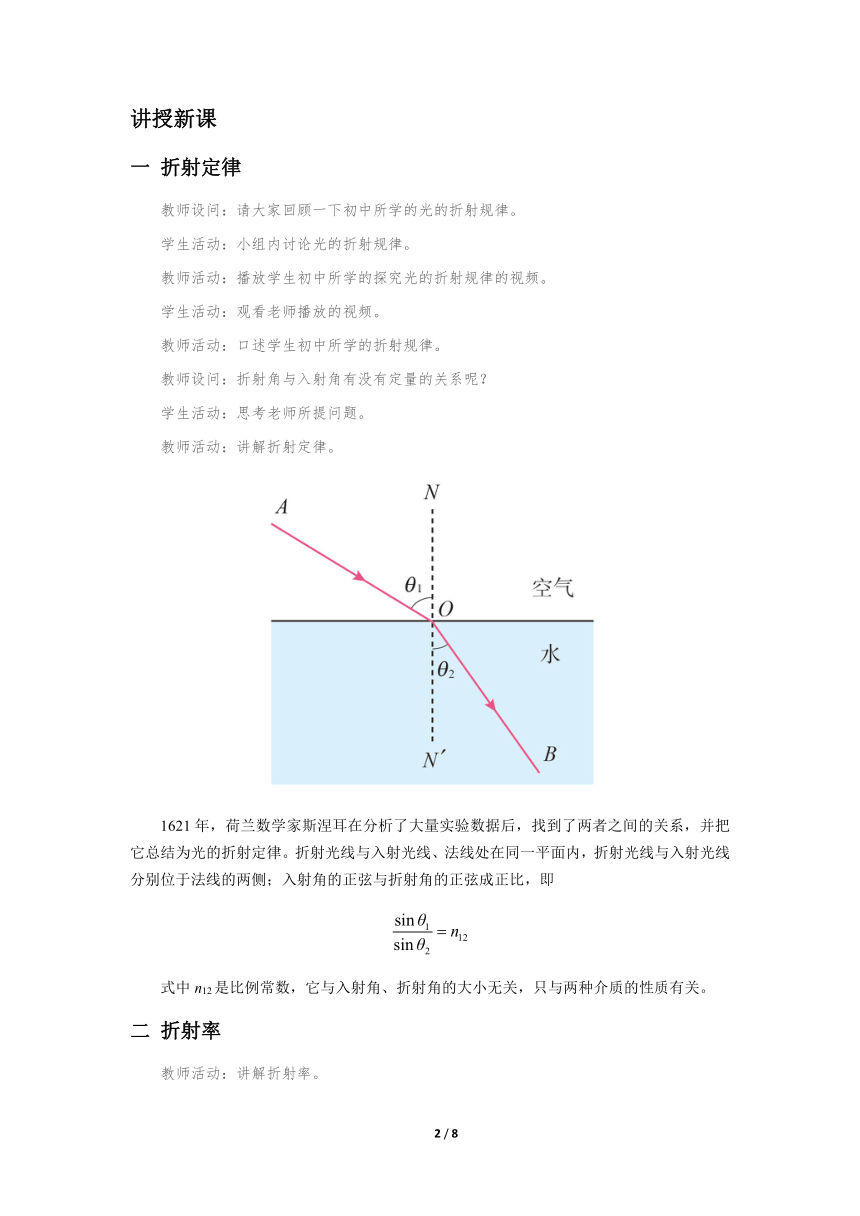
1621年,荷兰数学家斯涅耳在分析了大量实验数据后,找到了两者之间的关系,并把它总结为光的折射定律。折射光线与入射光线、法线处在同一平面内,折射光线与入射光线分别位于法线的两侧;入射角的正弦与折射角的正弦成正比,即
式中n12是比例常数,它与入射角、折射角的大小无关,只与两种介质的性质有关。
二 折射率
教师活动:讲解折射率。
从折射定律可知,光从一种介质射入另一种介质时,入射角的正弦值跟折射角的正弦值之比是一常数n12。一般说来,对不同的介质来说,这个常数n12是不同的。
由折射定律可知,常数n12越大,光线偏折越厉害。为了表征介质的这种性质,在物理学中引入折射率的概念,并把真空的折射率确定为1,而把光从真空射入某种介质发生折射时,入射角θ1的正弦值与折射角θ2的正弦值之比n,叫作这种介质的折射率,即
折射率与介质的自身性质有关,与入射角大小无关,是一个反映介质的光学性质的物理量。
由于空气的折射率与真空的折射率相差很小,一般情况下,可以把光从空气射入某种介质时入射角的正弦值与折射角的正弦值之比当作是这种介质的折射率。
不同介质的折射率不同,是由光在不同的介质中的传播速度不同引起的,折射率n与光在此介质中的传播速度v的关系为
其中,c为真空中的光速。
由于真空中光速最大,故所有介质的折射率都大于1,且折射率越大,光在此介质中的传播速率越小。
三 测量玻璃的折射率
教师活动:讲解实验原理。
用插针法确定入射光线和折射光线。画出法线测出入射角θ1和折射角θ2,则n=。
实验器材
教师设问:请同学们根据我们的实验设计,列举出实验所需要的器材。
学生活动:小组内讨论实验所需要的器材,然后小组代表发言。
教师活动:理答。
实验所需要的器材:玻璃砖、白纸、木板、大头针四枚、图钉四枚、量角器、直尺、铅笔。
实验步骤
教师口述:请同学们根据前面的实验设计和选定的实验器材制订细致的实验操作步骤。
学生活动:小组内讨论实验操作步骤,然后小组代表发言。
教师活动:理答。
(1)如图所示,将白纸用图钉钉在平木板上。
(2)在白纸上画出一条直线aa′作为界面(线),过aa′上的一点O画出界面的法线NN′,并画一条线段AO作为入射光线。
(3)把长方形玻璃砖放在白纸上,使它的长边跟aa′对齐,画出玻璃砖的另一边bb′。
(4)在直线AO上竖直插上两枚大头针P1、P2,透过玻璃砖观察大头针P1、P2的像,调整视线方向直到P2的像挡住P1的像。再在观察者一侧竖直插上两枚大头针P3、P4,使P3挡住P1、P2的像,P4挡住P3及P1、P2的像,记下P3、P4的位置。
(5)移去大头针和玻璃砖,过P3、P4所在处作直线O′B与bb′交于O′,直线O′B就代表了沿AO方向入射的光线通过玻璃砖后的传播方向。
(6)连接OO′,入射角θ1=∠AON,折射角θ2=∠O′ON′,用量角器量出入射角和折射角。
(7)用上述方法测出入射角分别为30°、45°、60°时的折射角。
师生活动:学生分组进行实验,教师作必要指导。
数据处理
教师设问:请同学们思考怎样通过这些数据来求玻璃的折射率。
学生活动:小组内讨论老师所提问题。
教师活动:讲解数据处理方法。
(1)计算法:用量角器测量入射角θ1和折射角θ2,并查出其正弦值sin θ1和sin θ2。算出不同入射角时的,并取平均值。
(2)单位圆法
以入射点O为圆心,以一定长度R为半径画圆,交入射光线OA于E点,交折射光线OO′于E′点,过E作NN′的垂线EH,过E′作NN′的垂线E′H′。如图所示,sin θ1=,sin θ2=,OE=OE′=R,则n==。只要用刻度尺测出EH、E′H′的长度就可以求出n。
(3)图像法
改变不同的入射角θ1,测出不同的折射角θ2,作sin θ1-sin θ2图象,由n=可知图像应为直线,如图所示,其斜率为折射率。
教师设问:请同学思考实验中误差的来源。
学生活动:小组内讨论老师所提问题,然后小组代表发言。
教师活动:讲解实验中误差可能的来源。
(1)入射光线、出射光线确定的准确性造成误差,故入射侧、出射侧所插两枚大头针间距应大一些。
(2)入射角和折射角的测量造成误差,故入射角应适当大些,以减小测量的相对误差。
典题剖析
例1 如图,一艘帆船静止在湖面上,帆船的竖直桅杆顶端高出水面3 m。距水面4 m的湖底P点发出的激光束,从水面出射后恰好照射到桅杆顶端,该出射光束与竖直方向的夹角为53°(取sin 53°=0.8)。已知水的折射率为。
(1)求桅杆到P点的水平距离;
(2)船向左行驶一段距离后停止,调整由P点发出的激光束方向,当其与竖直方向夹角为45°时,从水面射出后仍照射在桅杆顶端,求船行驶的距离。
解:(1)设光束从水面射出的点到桅杆的水平距离为x1,到P点的水平距离为x2;桅杆高度为h1,P点处水深为h2;激光束在水中与竖直方向的夹角为θ.由几何关系有
=tan 53° ①
=tan θ ②
由折射定律有
sin 53°=nsin θ ③
设桅杆到P点的水平距离为x,则
x=x1+x2 ④
联立①②③④式并代入题给数据得
x=7 m ⑤
(2)设激光束在水中与竖直方向的夹角为45°时,从水面出射的方向与竖直方向夹角为i′,由折射定律有
sin i′=nsin 45° ⑥
设船向左行驶的距离为x′,此时光束从水面射出的点到桅杆的水平距离为x1′,到P点的水平距离为x2′,则
x1′+x2′=x′+x ⑦
=tan i′ ⑧
=tan 45° ⑨
联立⑤⑥⑦⑧⑨式并代入题给数据得
x′=(6-3) m≈5.5 m ⑩
例2 某小组做测定玻璃的折射率实验,所用器材有:玻璃砖,大头针,刻度尺,圆规,笔,白纸。
(1)下列哪些措施能够提高实验准确程度________。
A.选用两光学表面间距大的玻璃砖
B.选用两光学表面平行的玻璃砖
C.选用粗的大头针完成实验
D.插在玻璃砖同侧的两枚大头针间的距离尽量大些
(2)该小组用同一套器材完成了四次实验,记录的玻璃砖界线和四个大头针扎下的孔洞如下图所示,其中实验操作正确的是________。
(3)该小组选取了操作正确的实验记录,在白纸上画出光线的径迹,以入射点O为圆心作圆,与入射光线、折射光线分别交于A、B点,再过A、B点作法线NN′的垂线,垂足分别为C、D点,如图所示,则玻璃的折射率n=________。(用图中线段的字母表示)
解析:(1)测玻璃的折射率关键是根据入射光线和出射光线确定在玻璃中的传播光线,因此选用光学表面间距大的玻璃砖以及使同侧两枚大头针的距离大些都有利于提高实验准确程度,减小误差;两光学表面是否平行不影响折射率的测量,为减小误差,应选用细长的大头针,故选B、C错误。
(2)两光学表面平行的玻璃砖的入射光线与出射光线平行,在空气中的入射角大于玻璃中的折射角,画图可知正确的图为D。
(3)玻璃的折射率n=,又sin i=,sin r=,故n=。
课堂小结
2 / 2
教学分析
学生在初中阶段已经接触过光的折射等知识,本节课属于人教版2019第四章第一节内容,教师要帮助学生在已有的知识基础上理解和掌握光的折射现象,要通过实验探究掌握实验方法,解决具体问题。
教学课时
2个课时
教学目标
(1)掌握折射定律,能光的折射定律解决相关问题。
(2)掌握介质的折射率的概念。
(3)经历根据实验原理设计测量玻璃的折射率的过程。
教学重难点
教学重点
折射定律、折射率、实验设计、实验操作、数据处理
教学难点
折射定律、折射率、实验设计、数据处理
教学准备
多媒体课件、木板、白纸、图钉、大头针、玻璃砖、铅笔、直尺、量角器。
教学过程
新课引入
教师设问:潭清疑水浅,荷动知鱼散。这是唐代诗人储光羲《钓鱼湾》中的诗句。为什么潭清疑水浅?这就是我们这节课要解决的问题。
讲授新课
一 折射定律
教师设问:请大家回顾一下初中所学的光的折射规律。
学生活动:小组内讨论光的折射规律。
教师活动:播放学生初中所学的探究光的折射规律的视频。
学生活动:观看老师播放的视频。
教师活动:口述学生初中所学的折射规律。
教师设问:折射角与入射角有没有定量的关系呢?
学生活动:思考老师所提问题。
教师活动:讲解折射定律。
1621年,荷兰数学家斯涅耳在分析了大量实验数据后,找到了两者之间的关系,并把它总结为光的折射定律。折射光线与入射光线、法线处在同一平面内,折射光线与入射光线分别位于法线的两侧;入射角的正弦与折射角的正弦成正比,即
式中n12是比例常数,它与入射角、折射角的大小无关,只与两种介质的性质有关。
二 折射率
教师活动:讲解折射率。
从折射定律可知,光从一种介质射入另一种介质时,入射角的正弦值跟折射角的正弦值之比是一常数n12。一般说来,对不同的介质来说,这个常数n12是不同的。
由折射定律可知,常数n12越大,光线偏折越厉害。为了表征介质的这种性质,在物理学中引入折射率的概念,并把真空的折射率确定为1,而把光从真空射入某种介质发生折射时,入射角θ1的正弦值与折射角θ2的正弦值之比n,叫作这种介质的折射率,即
折射率与介质的自身性质有关,与入射角大小无关,是一个反映介质的光学性质的物理量。
由于空气的折射率与真空的折射率相差很小,一般情况下,可以把光从空气射入某种介质时入射角的正弦值与折射角的正弦值之比当作是这种介质的折射率。
不同介质的折射率不同,是由光在不同的介质中的传播速度不同引起的,折射率n与光在此介质中的传播速度v的关系为
其中,c为真空中的光速。
由于真空中光速最大,故所有介质的折射率都大于1,且折射率越大,光在此介质中的传播速率越小。
三 测量玻璃的折射率
教师活动:讲解实验原理。
用插针法确定入射光线和折射光线。画出法线测出入射角θ1和折射角θ2,则n=。
实验器材
教师设问:请同学们根据我们的实验设计,列举出实验所需要的器材。
学生活动:小组内讨论实验所需要的器材,然后小组代表发言。
教师活动:理答。
实验所需要的器材:玻璃砖、白纸、木板、大头针四枚、图钉四枚、量角器、直尺、铅笔。
实验步骤
教师口述:请同学们根据前面的实验设计和选定的实验器材制订细致的实验操作步骤。
学生活动:小组内讨论实验操作步骤,然后小组代表发言。
教师活动:理答。
(1)如图所示,将白纸用图钉钉在平木板上。
(2)在白纸上画出一条直线aa′作为界面(线),过aa′上的一点O画出界面的法线NN′,并画一条线段AO作为入射光线。
(3)把长方形玻璃砖放在白纸上,使它的长边跟aa′对齐,画出玻璃砖的另一边bb′。
(4)在直线AO上竖直插上两枚大头针P1、P2,透过玻璃砖观察大头针P1、P2的像,调整视线方向直到P2的像挡住P1的像。再在观察者一侧竖直插上两枚大头针P3、P4,使P3挡住P1、P2的像,P4挡住P3及P1、P2的像,记下P3、P4的位置。
(5)移去大头针和玻璃砖,过P3、P4所在处作直线O′B与bb′交于O′,直线O′B就代表了沿AO方向入射的光线通过玻璃砖后的传播方向。
(6)连接OO′,入射角θ1=∠AON,折射角θ2=∠O′ON′,用量角器量出入射角和折射角。
(7)用上述方法测出入射角分别为30°、45°、60°时的折射角。
师生活动:学生分组进行实验,教师作必要指导。
数据处理
教师设问:请同学们思考怎样通过这些数据来求玻璃的折射率。
学生活动:小组内讨论老师所提问题。
教师活动:讲解数据处理方法。
(1)计算法:用量角器测量入射角θ1和折射角θ2,并查出其正弦值sin θ1和sin θ2。算出不同入射角时的,并取平均值。
(2)单位圆法
以入射点O为圆心,以一定长度R为半径画圆,交入射光线OA于E点,交折射光线OO′于E′点,过E作NN′的垂线EH,过E′作NN′的垂线E′H′。如图所示,sin θ1=,sin θ2=,OE=OE′=R,则n==。只要用刻度尺测出EH、E′H′的长度就可以求出n。
(3)图像法
改变不同的入射角θ1,测出不同的折射角θ2,作sin θ1-sin θ2图象,由n=可知图像应为直线,如图所示,其斜率为折射率。
教师设问:请同学思考实验中误差的来源。
学生活动:小组内讨论老师所提问题,然后小组代表发言。
教师活动:讲解实验中误差可能的来源。
(1)入射光线、出射光线确定的准确性造成误差,故入射侧、出射侧所插两枚大头针间距应大一些。
(2)入射角和折射角的测量造成误差,故入射角应适当大些,以减小测量的相对误差。
典题剖析
例1 如图,一艘帆船静止在湖面上,帆船的竖直桅杆顶端高出水面3 m。距水面4 m的湖底P点发出的激光束,从水面出射后恰好照射到桅杆顶端,该出射光束与竖直方向的夹角为53°(取sin 53°=0.8)。已知水的折射率为。
(1)求桅杆到P点的水平距离;
(2)船向左行驶一段距离后停止,调整由P点发出的激光束方向,当其与竖直方向夹角为45°时,从水面射出后仍照射在桅杆顶端,求船行驶的距离。
解:(1)设光束从水面射出的点到桅杆的水平距离为x1,到P点的水平距离为x2;桅杆高度为h1,P点处水深为h2;激光束在水中与竖直方向的夹角为θ.由几何关系有
=tan 53° ①
=tan θ ②
由折射定律有
sin 53°=nsin θ ③
设桅杆到P点的水平距离为x,则
x=x1+x2 ④
联立①②③④式并代入题给数据得
x=7 m ⑤
(2)设激光束在水中与竖直方向的夹角为45°时,从水面出射的方向与竖直方向夹角为i′,由折射定律有
sin i′=nsin 45° ⑥
设船向左行驶的距离为x′,此时光束从水面射出的点到桅杆的水平距离为x1′,到P点的水平距离为x2′,则
x1′+x2′=x′+x ⑦
=tan i′ ⑧
=tan 45° ⑨
联立⑤⑥⑦⑧⑨式并代入题给数据得
x′=(6-3) m≈5.5 m ⑩
例2 某小组做测定玻璃的折射率实验,所用器材有:玻璃砖,大头针,刻度尺,圆规,笔,白纸。
(1)下列哪些措施能够提高实验准确程度________。
A.选用两光学表面间距大的玻璃砖
B.选用两光学表面平行的玻璃砖
C.选用粗的大头针完成实验
D.插在玻璃砖同侧的两枚大头针间的距离尽量大些
(2)该小组用同一套器材完成了四次实验,记录的玻璃砖界线和四个大头针扎下的孔洞如下图所示,其中实验操作正确的是________。
(3)该小组选取了操作正确的实验记录,在白纸上画出光线的径迹,以入射点O为圆心作圆,与入射光线、折射光线分别交于A、B点,再过A、B点作法线NN′的垂线,垂足分别为C、D点,如图所示,则玻璃的折射率n=________。(用图中线段的字母表示)
解析:(1)测玻璃的折射率关键是根据入射光线和出射光线确定在玻璃中的传播光线,因此选用光学表面间距大的玻璃砖以及使同侧两枚大头针的距离大些都有利于提高实验准确程度,减小误差;两光学表面是否平行不影响折射率的测量,为减小误差,应选用细长的大头针,故选B、C错误。
(2)两光学表面平行的玻璃砖的入射光线与出射光线平行,在空气中的入射角大于玻璃中的折射角,画图可知正确的图为D。
(3)玻璃的折射率n=,又sin i=,sin r=,故n=。
课堂小结
2 / 2
