新人教版九年级上册数学《22.2 二次函数与一元二次方程》教案
文档属性
| 名称 | 新人教版九年级上册数学《22.2 二次函数与一元二次方程》教案 | 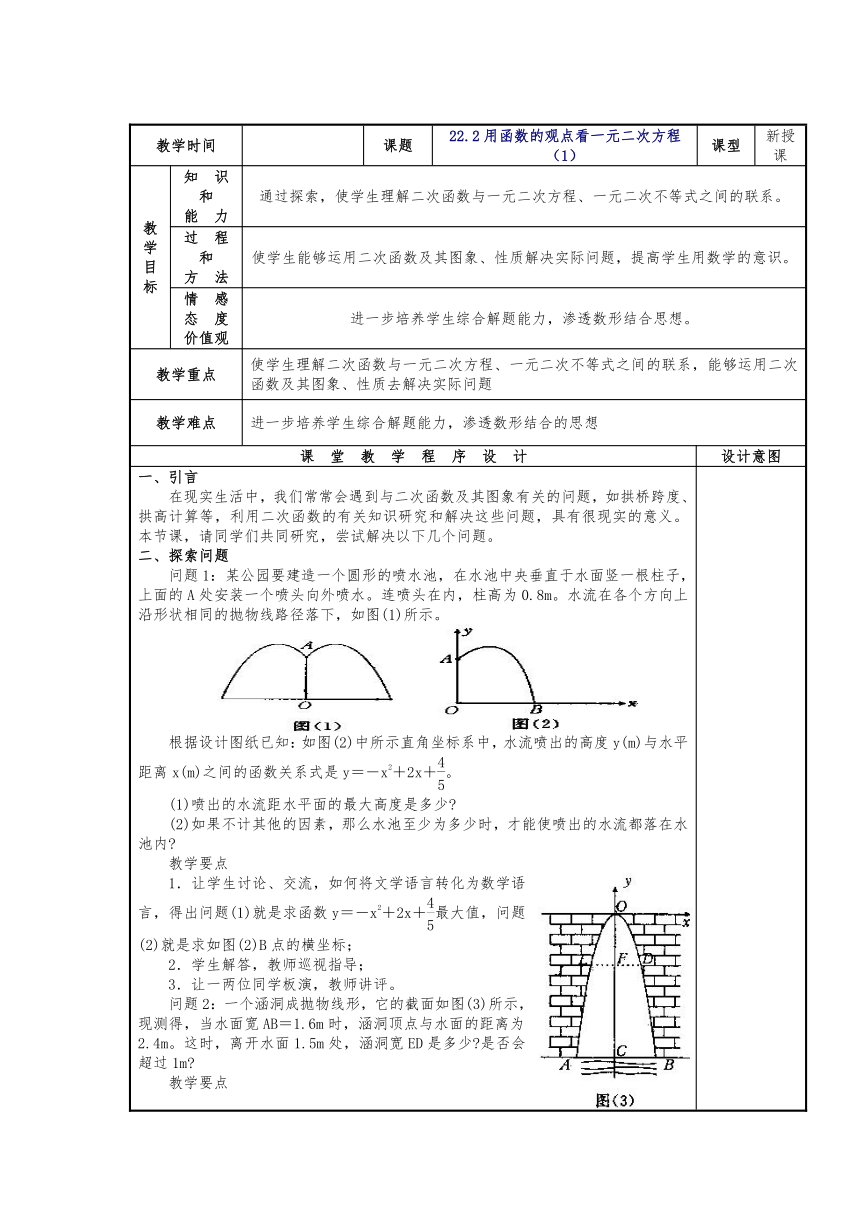 | |
| 格式 | zip | ||
| 文件大小 | 35.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-06-22 07:56:43 | ||
图片预览


文档简介
教学时间 课题 22.2用函数的观点看一元二次方程(1) 课型 新授课
教学目标 知 识和能 力 通过探索,使学生理解二次函数与一元二次方程、一元二次不等式之间的联系。
过 程和方 法 使学生能够运用二次函数及其图象、性质解决实际问题,提高学生用数学的意识。
情 感态 度价值观 进一步培养学生综合解题能力,渗透数形结合思想。
教学重点 使学生理解二次函数与一元二次方程、一元二次不等式之间的联系,能够运用二次函数及其图象、性质去解决实际问题
教学难点 进一步培养学生综合解题能力,渗透数形结合的思想
课 堂 教 学 程 序 设 计 设计意图
一、引言 在现实 ( http: / / www.21cnjy.com )生活中,我们常常会遇到与二 ( http: / / www.21cnjy.com )次函数及其图象有关的问题,如拱桥跨度、拱高计算等,利用二次函数的有关知识研究和解决这些问题,具有很现实的意义。本节课,请同学们共同研究,尝试解决以下几个问题。二、探索问题问题1:某公园要建造一个圆形的喷水池,在水 ( http: / / www.21cnjy.com )池中央垂直于水面竖一根柱子,上面的A处安装一个喷头向外喷水。连喷头在内,柱高为0.8m。水流在各个方向上沿形状相同的抛物线路径落下,如图(1)所示。 ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )根据设计图纸已知:如图(2)中所示直角坐标系中,水流喷出的高度y(m)与水平距离x(m)之间的函数关系式是y=-x2+2x+。(1)喷出的水流距水平面的最大高度是多少 (2)如果不计其他的因素,那么水池至少为多少时,才能使喷出的水流都落在水池内 教学要点1.让学生讨论、交流,如何将文学语言转化为 ( http: / / www.21cnjy.com )数学语言,得出问题(1)就是求函数y=-x2+2x+最大值,问题(2)就是求如图(2)B点的横坐标;2.学生解答,教师巡视指导;3.让一两位同学板演,教师讲评。问题2:一个涵洞成抛物线形 ( http: / / www.21cnjy.com ),它的截面如图(3)所示,现测得,当水面宽AB=1.6m时,涵洞顶点与水面的距离为2.4m。这时,离开水面1.5m处,涵洞宽ED是多少 是否会超过1m 教学要点1.教师分析:根据已知条件,要求ED的 ( http: / / www.21cnjy.com )宽,只要求出FD的长度。在如图(3)的直角坐标系中,即只要求出D点的横坐标。因为点D在涵洞所成的抛物线上,又由已知条件可得到点D的纵坐标,所以利用抛物线的函数关系式可以进一步算出点D的横坐标。2.让学生完成解答,教师巡视指导。3.教师分析存在的问题,书写解答过程。解:以AB的垂直平分线为y轴,以过点O的y轴的垂线为x轴,建立直角坐标系。这时,涵洞的横截面所成抛物线的顶点在原点,对称轴为y轴,开口向下,所以可设它的 函数关系式为:y=ax2 (a<0) (1)因为AB与y轴相交于C点,所以CB==0.8(m),又OC=2.4m,所以点B的坐标是(0.8,-2.4)。因为点B在抛物线上,将它的坐标代人(1),得 -2.4=a×0.82 所以:a=-因此,函数关系式是 y=-x2 (2)。。。。。。。。。。。。。。。。。。。。问题3:画出函数y=x2-x-3/4的图象,根据图象回答下列问题。(1)图象与x轴交点的坐标是什么;(2)当x取何值时,y=0 这里x的取值与方程x2-x-=0有什么关系 (3)你能从中得到什么启发 教学要点1.先让学生回顾函数y=ax2+bx+c图象的画法,按列表、描点、连线等步骤画出函数y=x2-x-的图象。2.教师巡视,与学生合作、交流。3.教师讲评,并画出函数图象,如图(4)所示。4.教师引导学生观察函数图象,回答(1)提出的问题,得到图象与x轴交点的坐标分别是(-,0)和(,0)。5.让学生完成(2)的解答。教师巡视指导并讲评。6.对于问题(3),教师组织学生分 ( http: / / www.21cnjy.com )组讨论、交流,各组选派代表发表意见,全班交流,达成共识:从“形”的方面看,函数y=x2-x-的图象与x轴交点的横坐标,即为方程x2-x-=0的解;从“数”的方面看,当二次函数y=x2-x-的函数值为0时,相应的自变量的值即为方程x2-x-=0的解。更一般地,函数y=ax2+bx+c的图象与x轴交点的横坐标即为方程ax2+bx+c=0的解;当二次函数y=ax2+bx+c的函数值为0时,相应的自变量的值即为方程ax2+bx+c=0的解,这一结论反映了二次函数与一元二次方程的关系。三、试一试 根据问题3的图象回答下列问题。 (1)当x取何值时,y<0 当x取何值时,y>0 (当-<x<时,y<0;当x<-或x>时,y>0) (2)能否用含有x的不等式 ( http: / / www.21cnjy.com )来描述(1)中的问题 (能用含有x的不等式采描述(1)中的问题,即x2-x-<0的解集是什么 x2-x->0的解集是什么 ) 想一想:二次函数与一元二次不等式有什么关系 让学生类比二次函数与一元二次不等式方程的关系,讨论、交流,达成共识: (1)从“形”的方面看,二次函数y= ( http: / / www.21cnjy.com )ax2+bJ+c在x轴上方的图象上的点的横坐标,即为一元二次不等式ax2+bx+c>0的解;在x轴下方的图象上的点的横坐标.即为一元二次不等式ax2+bx+c<0的解。 (2)从“数”的方 ( http: / / www.21cnjy.com )面看,当二次函数y=ax2+bx+c的函数值大于0时,相应的自变量的值即为一元二次不等式ax2+bx+c>0的解;当二次函数y=ax2+bx+c的函数值小于0时,相应的自变量的值即为一元二次不等式ax2+bc+c<0的解。这一结论反映了二次函数与一元二次不等式的关系。四、小结: 1.通过本节课的学习,你有什么收获 有什么困惑 2.若二次函数y=ax2+bx+c的图象与x轴无交点,试说明,元二次方程ax2+bx+c=0和一元二次不等式ax2+bx+c>0、ax2+bx+c<0的解的情况。
作业设计
教学反思
教学时间 课题 23.2用函数的观点看一元二次方程(2) 课型 新授课
教学目标 知 识和能 力 复习巩固用函数y=ax2+bx+c的图象求方程ax2+bx+c=0的解
过 程和方 法 让学生体验函数y=x2和y=bx+c的 ( http: / / www.21cnjy.com )交点的横坐标是方程x2=bx+c的解的探索过程,掌握用函数y=x2和y=bx+c图象交点的方法求方程ax2=bx+c的解。
情 感态 度价值观 提高学生综合解题能力,渗透数形结合思想。
教学重点 用函数图象法求方程的解以及提高学生综合解题能力
教学难点 提高学生综合解题能力,渗透数形结合的思想
教学准备 教师 多媒体课件 学生 “五个一”
课 堂 教 学 程 序 设 计 设计意图
一、复习巩固 1.如何运用函数y=ax2+bx+c的图象求方程ax2+bx+c的解 2.完成以下两道题: (1)画出函数y=x2+x-1的图象,求方程x2+x-1=0的解。(精确到0.1) (2)画出函数y=2x2-3x-2的图象,求方程2x2-3x-2=0的解。 教学要点 1.学生练习的同时,教师巡视指导, 2.教师根据学生情况进行讲评。 解:略 函数y=2x2-3x-2的图象与x轴交点的横坐标分别是x1=-和x2=2,所以一元二次方程的解是x1=-和x2=2。二、探索问题 问题1:(P23问题4)育才中 ( http: / / www.21cnjy.com )学初三(3)班学生在上节课的作业中出现了争论:求方程x2=x十3的解时,几乎所有学生都是将方程化为x2-x-3=0,画出函数y=x2-x-3的图象,观察它与x轴的交点,得出方程的解。唯独小刘没有将方程移项,而是分别画出了函数y=x2和y=x+2的图象,如图(3)所示,认为它们的交点A、B的横坐标-和2就是原方程的解. 提问: 1. 这两种解法的结果一样吗 2.小刘解法的理由是什么 让学生讨论,交流,发表不同意见,并进行归纳。 3.函数y=x2和y=bx+c的图象一定相交于两点吗 你能否举出例子加以说明 4,函数y=x2和y=bx+c的图象的交点横坐标一定是一元二次方程x2=bx+c的解吗 5.如果函数y=x2和y=bx+c图象没有交点,一元二次方程x2=bx+c的解怎样 三、做一做 利用图23.3.4,运用小刘方法求下列方程的解,并检验小刘的方法是否合理。 (1)x2+x-1=0(精确到0.1); (2)2x2-3x-2=0。 教学要点:①要把(1)的方程转化为x2=-x+1,画函数y=x2和y=-x+1的图象; ②要把(2)的方程转化为x ( http: / / www.21cnjy.com )2=x+1,画函数y=x2和y=x+1的图象;③在学生练习的同时,教师巡视指导;④解的情况分别与复习两道题的结果进行比较。四、综合运用 已知抛物线y1=2x2-8x+k+8和直线y2=mx+1相交于点P(3,4m)。 (1)求这两个函数的关系式; (2)当x取何值时,抛物线与直线相交,并求交点坐标。 解:(1)因为点P(3,4m)在直线y2=mx+1上,所以有4m=3m+1,解得m=1 所以y1=x+1,P(3,4)。 因为点P(3,4)在抛物线y1=2x2-8x+k+8上,所以有 4=18-24+k+8 解得 k=2 所以y1=2x2-8x+10 (2)依题意,得 解这个方程组,得, 所以抛物线与直线的两个交点坐标分别是(3,4),(1.5,2.5)。五、小结: 1.如何用画函数图象的方法求方程韵解 2.你能根据方程组:的解的情况,来判定函数y=x2与y=bx+c图象交点个数吗 请说说你的看法。
作业设计 必做
教学反思
教学目标 知 识和能 力 通过探索,使学生理解二次函数与一元二次方程、一元二次不等式之间的联系。
过 程和方 法 使学生能够运用二次函数及其图象、性质解决实际问题,提高学生用数学的意识。
情 感态 度价值观 进一步培养学生综合解题能力,渗透数形结合思想。
教学重点 使学生理解二次函数与一元二次方程、一元二次不等式之间的联系,能够运用二次函数及其图象、性质去解决实际问题
教学难点 进一步培养学生综合解题能力,渗透数形结合的思想
课 堂 教 学 程 序 设 计 设计意图
一、引言 在现实 ( http: / / www.21cnjy.com )生活中,我们常常会遇到与二 ( http: / / www.21cnjy.com )次函数及其图象有关的问题,如拱桥跨度、拱高计算等,利用二次函数的有关知识研究和解决这些问题,具有很现实的意义。本节课,请同学们共同研究,尝试解决以下几个问题。二、探索问题问题1:某公园要建造一个圆形的喷水池,在水 ( http: / / www.21cnjy.com )池中央垂直于水面竖一根柱子,上面的A处安装一个喷头向外喷水。连喷头在内,柱高为0.8m。水流在各个方向上沿形状相同的抛物线路径落下,如图(1)所示。 ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )根据设计图纸已知:如图(2)中所示直角坐标系中,水流喷出的高度y(m)与水平距离x(m)之间的函数关系式是y=-x2+2x+。(1)喷出的水流距水平面的最大高度是多少 (2)如果不计其他的因素,那么水池至少为多少时,才能使喷出的水流都落在水池内 教学要点1.让学生讨论、交流,如何将文学语言转化为 ( http: / / www.21cnjy.com )数学语言,得出问题(1)就是求函数y=-x2+2x+最大值,问题(2)就是求如图(2)B点的横坐标;2.学生解答,教师巡视指导;3.让一两位同学板演,教师讲评。问题2:一个涵洞成抛物线形 ( http: / / www.21cnjy.com ),它的截面如图(3)所示,现测得,当水面宽AB=1.6m时,涵洞顶点与水面的距离为2.4m。这时,离开水面1.5m处,涵洞宽ED是多少 是否会超过1m 教学要点1.教师分析:根据已知条件,要求ED的 ( http: / / www.21cnjy.com )宽,只要求出FD的长度。在如图(3)的直角坐标系中,即只要求出D点的横坐标。因为点D在涵洞所成的抛物线上,又由已知条件可得到点D的纵坐标,所以利用抛物线的函数关系式可以进一步算出点D的横坐标。2.让学生完成解答,教师巡视指导。3.教师分析存在的问题,书写解答过程。解:以AB的垂直平分线为y轴,以过点O的y轴的垂线为x轴,建立直角坐标系。这时,涵洞的横截面所成抛物线的顶点在原点,对称轴为y轴,开口向下,所以可设它的 函数关系式为:y=ax2 (a<0) (1)因为AB与y轴相交于C点,所以CB==0.8(m),又OC=2.4m,所以点B的坐标是(0.8,-2.4)。因为点B在抛物线上,将它的坐标代人(1),得 -2.4=a×0.82 所以:a=-因此,函数关系式是 y=-x2 (2)。。。。。。。。。。。。。。。。。。。。问题3:画出函数y=x2-x-3/4的图象,根据图象回答下列问题。(1)图象与x轴交点的坐标是什么;(2)当x取何值时,y=0 这里x的取值与方程x2-x-=0有什么关系 (3)你能从中得到什么启发 教学要点1.先让学生回顾函数y=ax2+bx+c图象的画法,按列表、描点、连线等步骤画出函数y=x2-x-的图象。2.教师巡视,与学生合作、交流。3.教师讲评,并画出函数图象,如图(4)所示。4.教师引导学生观察函数图象,回答(1)提出的问题,得到图象与x轴交点的坐标分别是(-,0)和(,0)。5.让学生完成(2)的解答。教师巡视指导并讲评。6.对于问题(3),教师组织学生分 ( http: / / www.21cnjy.com )组讨论、交流,各组选派代表发表意见,全班交流,达成共识:从“形”的方面看,函数y=x2-x-的图象与x轴交点的横坐标,即为方程x2-x-=0的解;从“数”的方面看,当二次函数y=x2-x-的函数值为0时,相应的自变量的值即为方程x2-x-=0的解。更一般地,函数y=ax2+bx+c的图象与x轴交点的横坐标即为方程ax2+bx+c=0的解;当二次函数y=ax2+bx+c的函数值为0时,相应的自变量的值即为方程ax2+bx+c=0的解,这一结论反映了二次函数与一元二次方程的关系。三、试一试 根据问题3的图象回答下列问题。 (1)当x取何值时,y<0 当x取何值时,y>0 (当-<x<时,y<0;当x<-或x>时,y>0) (2)能否用含有x的不等式 ( http: / / www.21cnjy.com )来描述(1)中的问题 (能用含有x的不等式采描述(1)中的问题,即x2-x-<0的解集是什么 x2-x->0的解集是什么 ) 想一想:二次函数与一元二次不等式有什么关系 让学生类比二次函数与一元二次不等式方程的关系,讨论、交流,达成共识: (1)从“形”的方面看,二次函数y= ( http: / / www.21cnjy.com )ax2+bJ+c在x轴上方的图象上的点的横坐标,即为一元二次不等式ax2+bx+c>0的解;在x轴下方的图象上的点的横坐标.即为一元二次不等式ax2+bx+c<0的解。 (2)从“数”的方 ( http: / / www.21cnjy.com )面看,当二次函数y=ax2+bx+c的函数值大于0时,相应的自变量的值即为一元二次不等式ax2+bx+c>0的解;当二次函数y=ax2+bx+c的函数值小于0时,相应的自变量的值即为一元二次不等式ax2+bc+c<0的解。这一结论反映了二次函数与一元二次不等式的关系。四、小结: 1.通过本节课的学习,你有什么收获 有什么困惑 2.若二次函数y=ax2+bx+c的图象与x轴无交点,试说明,元二次方程ax2+bx+c=0和一元二次不等式ax2+bx+c>0、ax2+bx+c<0的解的情况。
作业设计
教学反思
教学时间 课题 23.2用函数的观点看一元二次方程(2) 课型 新授课
教学目标 知 识和能 力 复习巩固用函数y=ax2+bx+c的图象求方程ax2+bx+c=0的解
过 程和方 法 让学生体验函数y=x2和y=bx+c的 ( http: / / www.21cnjy.com )交点的横坐标是方程x2=bx+c的解的探索过程,掌握用函数y=x2和y=bx+c图象交点的方法求方程ax2=bx+c的解。
情 感态 度价值观 提高学生综合解题能力,渗透数形结合思想。
教学重点 用函数图象法求方程的解以及提高学生综合解题能力
教学难点 提高学生综合解题能力,渗透数形结合的思想
教学准备 教师 多媒体课件 学生 “五个一”
课 堂 教 学 程 序 设 计 设计意图
一、复习巩固 1.如何运用函数y=ax2+bx+c的图象求方程ax2+bx+c的解 2.完成以下两道题: (1)画出函数y=x2+x-1的图象,求方程x2+x-1=0的解。(精确到0.1) (2)画出函数y=2x2-3x-2的图象,求方程2x2-3x-2=0的解。 教学要点 1.学生练习的同时,教师巡视指导, 2.教师根据学生情况进行讲评。 解:略 函数y=2x2-3x-2的图象与x轴交点的横坐标分别是x1=-和x2=2,所以一元二次方程的解是x1=-和x2=2。二、探索问题 问题1:(P23问题4)育才中 ( http: / / www.21cnjy.com )学初三(3)班学生在上节课的作业中出现了争论:求方程x2=x十3的解时,几乎所有学生都是将方程化为x2-x-3=0,画出函数y=x2-x-3的图象,观察它与x轴的交点,得出方程的解。唯独小刘没有将方程移项,而是分别画出了函数y=x2和y=x+2的图象,如图(3)所示,认为它们的交点A、B的横坐标-和2就是原方程的解. 提问: 1. 这两种解法的结果一样吗 2.小刘解法的理由是什么 让学生讨论,交流,发表不同意见,并进行归纳。 3.函数y=x2和y=bx+c的图象一定相交于两点吗 你能否举出例子加以说明 4,函数y=x2和y=bx+c的图象的交点横坐标一定是一元二次方程x2=bx+c的解吗 5.如果函数y=x2和y=bx+c图象没有交点,一元二次方程x2=bx+c的解怎样 三、做一做 利用图23.3.4,运用小刘方法求下列方程的解,并检验小刘的方法是否合理。 (1)x2+x-1=0(精确到0.1); (2)2x2-3x-2=0。 教学要点:①要把(1)的方程转化为x2=-x+1,画函数y=x2和y=-x+1的图象; ②要把(2)的方程转化为x ( http: / / www.21cnjy.com )2=x+1,画函数y=x2和y=x+1的图象;③在学生练习的同时,教师巡视指导;④解的情况分别与复习两道题的结果进行比较。四、综合运用 已知抛物线y1=2x2-8x+k+8和直线y2=mx+1相交于点P(3,4m)。 (1)求这两个函数的关系式; (2)当x取何值时,抛物线与直线相交,并求交点坐标。 解:(1)因为点P(3,4m)在直线y2=mx+1上,所以有4m=3m+1,解得m=1 所以y1=x+1,P(3,4)。 因为点P(3,4)在抛物线y1=2x2-8x+k+8上,所以有 4=18-24+k+8 解得 k=2 所以y1=2x2-8x+10 (2)依题意,得 解这个方程组,得, 所以抛物线与直线的两个交点坐标分别是(3,4),(1.5,2.5)。五、小结: 1.如何用画函数图象的方法求方程韵解 2.你能根据方程组:的解的情况,来判定函数y=x2与y=bx+c图象交点个数吗 请说说你的看法。
作业设计 必做
教学反思
同课章节目录
