山东省乐陵市第三中学2014-2015学年八年级下学期人教版数学《19.2 一次函数》学案
文档属性
| 名称 | 山东省乐陵市第三中学2014-2015学年八年级下学期人教版数学《19.2 一次函数》学案 |

|
|
| 格式 | zip | ||
| 文件大小 | 290.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-06-22 00:00:00 | ||
图片预览




文档简介
19.2.1 正比例函数
警示语:K正一三负二四,变化趋势记心间。
K正左低右边高,同大同小向爬山。
K负左高右边低,一大另小下山峦。
学习目标
1、理解正比例函数的概念
2、会画正比例函数的图像,理解正比例函数的性质。
四、检查预习情况
按下列要求写出解析式
(1)一本笔记本的单价为2元,现购买x本与付费y元的关系式为_________________;
(2)若正方形的周长为P,边长为a,那么边长a与周长p之间的关系式为______________;
(3)一辆汽车的速度为60 km / h ,则行使路程s与行使时间t之间的关系式为___________;
(4)圆的半径为r,则圆的周长c与半径r之间的关系式为
五、小组讨论、合作探究:
探究(一)
在上述问题中变量之间的对应关系是函数关系吗?如果是,这些函数解析式有哪些共同的特征?
一般地,形如 (k是常数,k≠0)的函数,叫做正比例函数,其中 叫做比例系数。
1、下列函数,那些是正比例函数?______________
(1) (2) (3) (4)
(5) (6) (7)
(8)
2、关于x的函数是正比例函数,则m__________
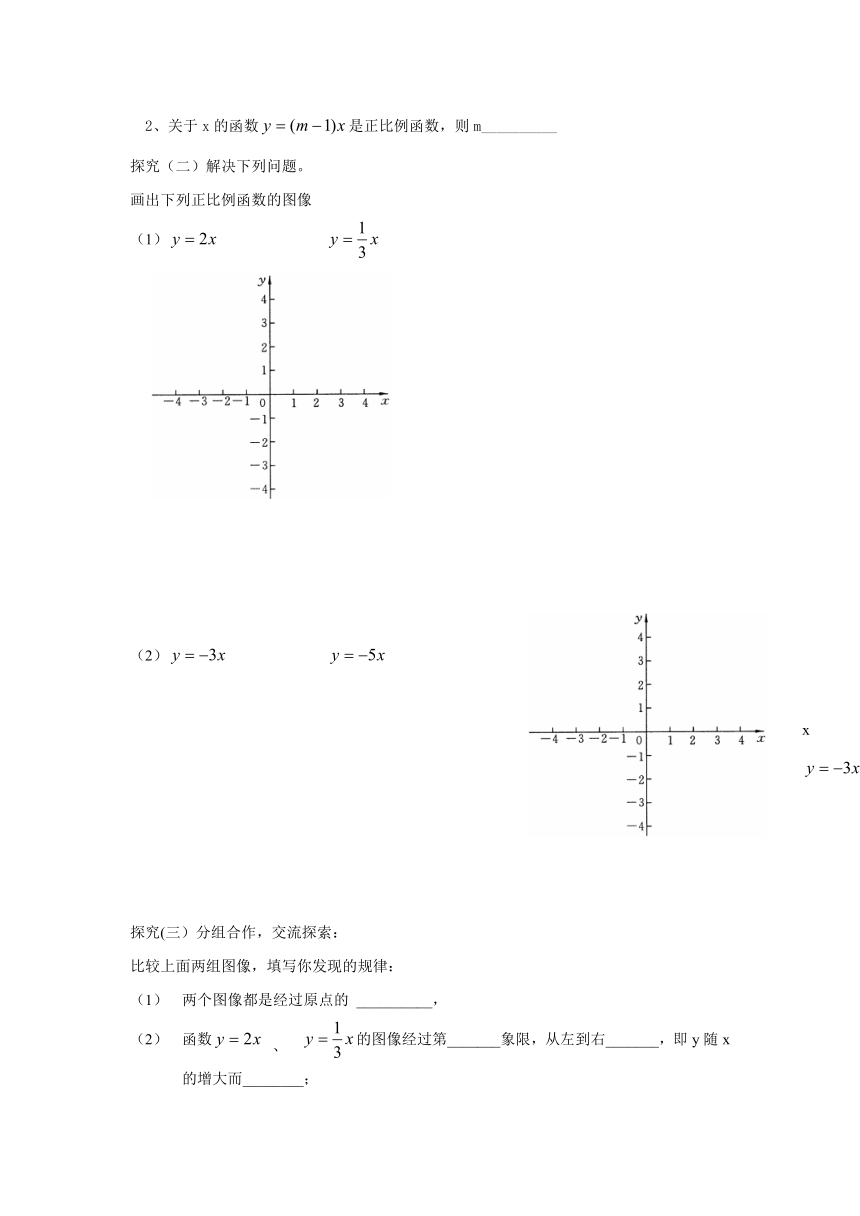
探究(二)解决下列问题。
画出下列正比例函数的图像
(1)
x -2 -1 0 1 2
(2)
x -2 -1 0 1 2
探究(三)分组合作,交流探索:
比较上面两组图像,填写你发现的规律:
两个图像都是经过原点的 __________,
函数 、 的图像经过第_______象限,从左到右_______,即y随x的增大而________;
函数 、 的图像经过第_______象限,从左到右_______,即y随x的增大而________;
总结:正比例函数的解析式为__________________
相同点
图像所在象限
图像大致形状
增减性
展示汇报、质疑答疑:
因为两点确定一条直线,所以可用两点法画正 ( http: / / www.21cnjy.com )比例函数y=kx(k≠0)图像 。方法:过( )和( )的直线就是
七、拓展延伸:
用你认为最简单的方法画出下列函数的图像。
Y=0.5x y= -2x
七、目标回应:
1、_______________________________________
2、
九、作业:必作题:
1、关于函数,下列结论中,正确的是( )
A、函数图像经过点(1,3) B、函数图像经过二、四象限
C、y随x的增大而增大 D、不论x为何值,总有y>0
2、已知正比例函数的图像过第二、四象限,则( )
A、y随x的增大而增大 B、y随x的增大而减小
C、当时,y随x的增大而增大;当时,y随x的增大而减少;
D、不论x如何变化,y不变。
3、当时,函数的图像在第( )象限。
A、一、三 B、二、四 C、二 D、三
4、函数的图像经过点P(-1,3)则k的值为( )
A、3 B、—3 C、 D、
5、若A(1,m)在函数的图像上,则m=________,则点A关于y轴对称点坐标是___________;
6、若B(m,6)在函数的图像上,则m=________,则点A关于x轴对称点坐标是___________;
达标测试:
1、y与x成正比例,当x=3时,,则y关于x的函数关系式是____________
2、函数的图像在第_______象限,经过点(0,____)与点(1,____),y随x的增大而_________
3、一个函数的图像是经过原点的直线,并且这条直线经过点(1,-3),求这个函数解析式。
19.2.2 一次函数(一)
警示语: K正左低右边高,越走越高向爬山。 ( http: / / www.21cnjy.com )
K负左高右边低,越来越低很明显。
K称斜率b截距,截距为零变正函。
课前展示:
复习什么叫正比例函数,并举例说明。
复习正比例函数的图像和性质。
学习目标:
1、掌握一次函数解析式的特点及意义
2、理解一次函数与正比例函数的关系.
3、会画一次函数的图象
四、检查预习情况
根据题意写出下列函数的解析式
有人发现,在20~25℃时蟋蟀每分鸣叫次数c与温度t(单位:℃)有关,即c的值约是t的7倍与35的差;_______________
一种计算成年人标准体重G(单位:千克)的方法是,以厘米为单位量出身高值h,再减常数105,所得的差是G的值;_______________
某城市的市内电话的月收费为y(单位:元)包括:月租22元,拨打电话x分的计时费(按0.1元/分收取);_______________
把一个长10cm、宽5cm的长方形的长减少xcm,宽不变,长方形的面积y(单位:cm2)随x的值而变化。_______________
五、小组讨论、合作探究:
探究(一)
在上述问题中变量之间的对应关系是函数关系吗?如果是,这些函数解析式有哪些共同的特征?
一般地,形如 (k,b是常数,)的函数,叫做一次函数,特别地,当 时,即,即正比例函数是一种特殊的一次函数。
探究(二)
分组合作;交流探索:
下列函数中,是一次函数的有_____________,是正比例函数的有______________
(1) (2) (3) (4)
(5) (6) (7)
2、若函数是正比例函数,则b = _________
六、展示汇报、质疑答疑:
七、拓展延伸:
1、在一次函数中,k =_______,b =________
2、若函数是一次函数,则m__________
3、在一次函数中,当时,______;当_____时,。
八、目标回应:
1、_______________________________________
2、
九、作业:必作题:
1、下列说法正确的是( )
A、是一次函数 B、一次函数是正比例函数
C、正比例函数是一次函数 D、不是正比例函数就一定不是一次函数
2、仓库内原有粉笔400盒,如果每个星期领 ( http: / / www.21cnjy.com )出36盒,则仓库内余下的粉笔盒数Q与星期数t之间的函数关系式是________________,它是__________函数。
3、随着海拔高度的升高,大 ( http: / / www.21cnjy.com )气压下降,空气的含氧量也随之下降,已知含氧量y与大气压强x成正比例,当x=36时,y=108,请写出y与x的函数解析式___________,这个函数图像在第________象限,同时经过点(0,_____)与点(1,_____)
4.若函数y=(m-1)x+m是关于x的一次函数,试求m的值.
5、下列说法不正确的是( )
(A)一次函数不一定是正比例函数 (B)不是一次函数就一定不是正比例函数
(C)正比例函数是特定的一次函数 (D)不是正比例函数就不是一次函数
6.已知函数y=(2-m)x+2m-3.求当m为何值时,
(1)此函数为正比例函数
(2)此函数为一次函数
.《达标测试》:
一个小球由静止开始在一个斜坡向下滚动,其速度每秒增加2米。
(1)求小球速度v随时间t变化的函数关系式,它是一次函数吗?(2)求第2.5秒时小球的速度?
8、梯形的上底长x,下底长15,高8;
(1)写出梯形的面积y与上底x的关系式,是一次函数吗 ( http: / / www.21cnjy.com )
(2)当x每增加1时, y是如何变化的
(3)当x=0时, y等于多少?此时y的意义是什么
10.若函数y=mx-(4m-4)的图 ( http: / / www.21cnjy.com )象过原点,则m=_______,此时函数是______函数.若函数y=mx-(4m-4)的图象经过(1,3)点,则m=______,此时函数是______函数.
11.在同一坐标系中作出函数Y=2X+3和y=-2x+3的图像。
19.2.2一次函数(二)
警示语:一次函数图直线,经过(0, ( http: / / www.21cnjy.com )b)这个点。
K正左低右边高,越走越高向爬山。
K负左高右边低,越来越低很明显。
K称斜率b截距,截距为零变正函。
课前展示:
一次函数的定义
学习目标:
1.知道一次函数图象的特点,知道一次函数与正比例函数图象之间的关系.。毛
2.理解一次函数图像的性质,了解中的k,b对函数图像的影响
3.会熟练地画一次函数的图象.
四、检查预习情况
在同一个直角坐标系中画出函数,,的图像
-2 -1 0 1 2
y=2x
y=2x+3
y=2x-3
五、小组讨论、合作探究:
探究(一)
分组合作,交流探索:
观察这三个图像,这三个函数图像形状都是________,并且倾斜度_______。函数
的图像经过原点,函数与y轴交于点________,即它可以看作由直线向_____平移_____个单位长度得到;同样的,函数与y轴交于点
________,即它可以看作由直线向_____平移_____个单位长度得到。
探究(二)解决下列问题。
比较一次函数y=kx+b(k≠0)与正比例函数y=kx(k≠0)的解析式与图像你能得到二者的关系吗?
一次函数y=kx+b(k≠0)的图像是一条________,它可以由直线( )平移( )个单位长度得到,当时,它是由直线y=kx(k≠0)向_____平移_____个单位长度得到;当时,它是由直线y=kx(k≠0)向_____平移_____个单位长度得到。
展示汇报、质疑答疑:
在同一个直角坐标系中,把直线向_______平移_____个单位就得到的图像;若向_______平移_____个单位就得到的图像。
将直线向下平移2个单位,可得直线________;
3、将直线向_____平移______个单位可得直线
七、拓展延伸:
1、(1)将直线y=3x向下平移2个单位,得到直线 ;
(2)将直线y=-x-5向上平移5个单位,得到直线 ;
(3)将直线y=-2x+3向下平移5个单位,得到直线 .
2、函数y=kx-4的图象平行于直线y=-2x,求函数的表达式.
八、目标回应:
1、_______________________________________
2、
九、作业:必作题:
1、直线y=kx+b可以看作由直线 ( http: / / www.21cnjy.com )y=kx平移_____个单位而得到,当b>0时,向_____平移,当b<0时,向_____平移。即k值相同时,直线一定平行。
2.在不同坐标系中作出下列函数的图象:
(1)y=3x+2 (2)y= -3x+2 (3)y=3x-2 (4)y= -3x-2
《达标测试》:
一次函数y=kx+b的图象与y轴交于点(0,-2),且与直线平行,求它的函数表达式.
19.2.2一次函数(三)
一、警示语:一次函数图直线,经过(0,b)这 ( http: / / www.21cnjy.com )个点。
K正左低右边高,越走越高向爬山。
K负左高右边低,越来越低很明显。
K称斜率b截距,截距为零变正函。
二、课前展示:
在同坐标系中作出下列函数的图象:
(2)
学习目标:
1、理解一次函数图像的性质,了解中的k,b对函数图像的影响
2.会熟练地画一次函数的图象.
四、检查预习情况
在同坐标系中作出下列函数的图象:
(3) (4)
五、小组讨论、合作探究:
探究(一)
观察上面四个图像,
经过_________象限;y随x的增大而_______,函数的图像从左到右________;
(2)经过_________象限;y随x的增大而_______,函数的图像从左到右________;
(3)经过_________象限;y随x的增大而_______,函数的图像从左到右________;
(4)经过_________象限;y随x的增大而_______,函数的图像从左到右________。
1、由此可以得到直线中, 的取值决定直线的位置:
(1)直线经过___________象限;
(2)直线经过___________象限;
(3)直线经过___________象限;
(4)直线经过___________象限;
2、一次函数的性质:
(1)当时,y随x的增大而_______,这时函数的图像从左到右_______;
(2)当时,y随x的增大而_______,这时函数的图像从左到右_______;
六、展示汇报、质疑答疑:
七、拓展延伸:
1.已知一次函数y=(2m-1)x+m+5,当m是什么数时,函数值y随x的增大而减小?
2.已知一次函数y=(1-2m)x+m-1,若函数y随x的增大而减小,并且函数的图象经过二、三、四象限,求m的取值范围.
八、目标回应:
1、_______________________________________
2、
九、作业:必作题:
选择题:
1、一次函数的图像不经过( )
第一象限 B、第二象限
C、 第三想象限 D、 第四象限
2、已知直线不经过第三象限,也不经过原点,则下列结论正确的是( )
A、 B、
C、 D、
3、下列函数中,y随x的增大而增大的是( )
A、 B、
C、 D、
4、对于一次函数,函数值y随x的增大而减小,则k的取值范围是( )
A、 B、 C、 D、
5、一次函数的图像一定经过( )
A、(3,5) B、(-2,3) C、(2,7) D、(4、10)
6、已知正比例函数的函数值y随x的增大而增大,则一次函数的图像大致是( )
7、一次函数的图像如图所示,则k_______,b_______,y随x的增大而_________
8、一次函数的图像经过___________象限,y随x的增大而_________
《达标测试》:
9、已知点(-1,a)、(2,b)在直线 上,则a,b的大小关系是__________
10、直线与x轴交点坐标为__________;与y轴交点坐标_________;图像经过__________象限,y随x的增大而____________,图像与坐标轴所围成的三角形的面积是___________
11、已知一次函数的图像经过点(0,1),且y随x的增大而增大,请你写出一个符合上述条件的函数关系式_____________
12、已知一次函数图像(1 ( http: / / www.21cnjy.com ))不经过第二象限,(2)经过点(2,-5),请写出一个同时满足(1)和(2)这两个条件的函数关系式:_______________
一、警句:一次函数图直线 ( http: / / www.21cnjy.com ),经过(0,b)这个点。
K正左低右边高,越走越高向爬山。
K负左高右边低,越来越低很明显。
K称斜率b截距,截距为零变正函。
二、课前展示:
复习一次函数的性质及画图像的方法。
学习目标:
1.了解两个条件确定一个一次函数;一个条件确定一个正比例函数.
2.能由两个条件求出一次函数的表达式,一个条件求出正比例函数的表达式.
3能根据函数的图象确定一次函数的表达式,培养学生的数形结合能力.
检查预习情况
一次函数关系式y=kx+b(k≠0),如果知道了k与b的值,函数解析式就确定了,那么有怎样的条件才能求出k和b呢?
已知一次函数的图像经过点(3,5)与(2,3),求这个一次函数的解析式。
分析:求一次函数的解析式,关键是求出k,b的值,从已知条件可以列出关于k,b的二元一次方程组,并求出k,b。
解: ∵一次函数经过点(3,5)与(2,3)
∴
解得
∴一次函数的解析式为_______________
像这样先设出函数解析式,再根据条件确定 ( http: / / www.21cnjy.com )解析式中未知的系数,从而具体写出这个式子的方法,叫做
五、小组讨论、合作探究:
探究(一)
1、已知一次函数,当x = 5时,y = 4,
(1)求这个一次函数。 (2)求当时,函数y的值。
2、.已知一次函数y=kx+b的图象经过点(-1,1)和点(1,-5),求当x=5时,函数y的值.
展示汇报、质疑答疑:
(函数解析式y=kx+b) (满足条件的两个点) 一次函数
(x1 , y1)与(x2 , y2) 的图像
拓展延伸:
黄金一号玉米种子的价格为5元/kg,如果一次购买2kg以上的种子,超过2kg部分的种子价格打8折.
1、完成下表:
购买量/kg 0.5 1 1.5 2 2.5 3 ......
付款金额/元
2、写出购买量关于付款金额的函数解析式,并画出函数的图像。
八、目标回应:
1、_______________________________________
2、
九、作业:必作题:
1、已知弹簧的长度 y(厘米)在一定的 ( http: / / www.21cnjy.com )限度内是所挂重物质量 x(千克)的一次函数.现已测得不挂重物时弹簧的长度是6厘米,挂4千克质量的重物时,弹簧的长度是7.2厘米.求这个一次函数的关系式.
2:已知一次函数的图象如图所示,求出它的函数关系式
3、某自来水公司为了鼓励市民节约用水,采取分段收费标准。居民每月应交水费y(元)是用水量x(吨)的函数,其图象如图所示:
分别写出和时,y与x的函数解析式;
若某用户居民该月用水3.5吨,问应交水费多少元?
若该月交水费9元,则用水多少吨?
《达标测试》:
1、求函数与x轴、y轴的交点坐标,并求这条直线与两坐标轴围成的三角形的面积.
2、某运输公司规定每名旅客行李托运费与所托运行李质量之间的关系式如图所示,请根据图像回答下列问题:
(1)、由图像可知,行李质量只要不超过______kg,就可以免费携带。如果超过了规定的质量,则每超过10kg,要付费_______元。
(2)若旅客携带的行李质量为x(kg),所付的行李费是y(元),请写出y(元)随x(kg)变化的关系式。
(3)若王先生携带行李50kg,他共要付行李费多少元?
19.2.3 一次函数与一元一次方程
警句:一次函数图直线,经过(0,b ( http: / / www.21cnjy.com ))这个点。
K正左低右边高,越走越高向爬山。
K负左高右边低,越来越低很明显。
课前展示:
复习一元一次方程及标准形式的意义。
复习不等式的意义
学习目标:
1、用函数观点认识一元一次方程,认识一元一次不等式与一次函数问题的转化关系.毛
2.学会用图象法求解不等式.
3.进一步理解数形结合思想.
检查预习情况
1、解方程2x+20=0
2.当自变量x为何值时,函数y=2x+20的值为0?
这两个问题之间有什么联系吗?
1.解不等式2x-4>0
2.当自变量x为何值时函数y=2x-4的值大于0?
这两个问题之间有什么联系吗?
五、小组讨论、合作探究:
探究(一)
下面三个方程有什么共同点和不同点?你能从函数的角度对解这三个方程进行解释吗?
(1) 2x+1=3 (2) 2x+1=0 (3)2x+1=-1
结论:
探究(二)
下面三个不等式有什么共同点和不同点?你能从函数的角度对解这三个不等式进行解释吗?
(1) 2x+1>3 (2) 2x+1<0 (3)2x+1<-1
结论:
展示汇报、质疑答疑:
1、若直线y=kx+6与两坐标轴所围成的三角形面积是24,求常数k的值是多少?
分析:(1)一次函数的图象与两条坐标轴围 ( http: / / www.21cnjy.com )成的图形是直角三角形,两条直角边的长分别是图象与x轴的交点的横坐标的绝对值和与y轴的交点的纵坐标的绝对值.
(2)确定图象与两条坐标轴的交点坐标可以通过令x=0和y=0解方程求得.
七、拓展延伸:
2、已知函数y1=kx-2和y2=-3x+b相交于点A(2,-1)
(1)求k、b的值,在同一坐标系中画出两个函数的图象.
(2)利用图象求出:当x取何值时有:①y1(3)利用图象求出:当x取何值时有:①y1<0且y2<0;②y1>0且y2<0
八、目标回应:
1、_______________________________________
2、
九、作业:必作题:
1.直线y=3x+9与x轴的交点是( )
A.(0,-3) B.(-3,0) C.(0,3) D.(0,-3)
2.直线y=kx+3与x轴的交点是(1,0),则k的值是( )
A.3 B.2 C.-2 D.-3
3.已知直线y=kx+b与直线y=3x-1交于y轴同一点,则b的值是( )
A.1 B.-1 C. D.-
4.已知直线AB∥x轴,且点A的坐标是(-1,1),则直线y=x与直线AB的交点是( )
A.(1,1) B.(-1,-1) C.(1,-1) D.(-1,1)
5.直线y=3x+6与x轴的交点的横坐标x的值是方程2x+a=0的解,则a的值是______.
6.已知直线y=2x+8与x轴和y轴 ( http: / / www.21cnjy.com )的交点的坐标分别是_______、_______.与两条坐标轴围成的三角形的面积是__________.
7.已知关于x的方程mx+n=0的解是x=-2,则直线y=mx+n与x轴的交点坐标是________.
8.方程3x+2=8的解是__________,则函数y=3x+2在自变量x等于_________时的函数值是8.
1.直线y=x-1上的点在x轴上方时对应的自变量的范围是( )
A.x>1 B.x≥1 C.x<1 D.x≤1
2.已知直线y=2x+k与x轴的交点为(-2,0),则关于x的不等式2x+k<0的解集是( )
A.x>-2 B.x≥-2 C.x<-2 D.x≤-2
3.已知关于x的不等式ax+1>0(a≠0)的解集是x<1,则直线y=ax+1与x轴的交点是( )
A.(0,1) B.(-1,0) C.(0,-1) D.(1,0)
4.当自变量x的值满足____________时,直线y=-x+2上的点在x轴下方.
5.已知直线y=x-2与y=-x+2相交于点(2,0),则不等式x-2≥-x+2的解集是________.
6.直线y=-3x-3与x轴的交点坐标是________,则不等式-3x+9>12的解集是________.
7.已知关于x的不等式kx-2>0(k≠0)的解集是x>-3,则直线y=-kx+2与x轴的交点是__________.
《达标测试》:
有一个一次函数的图象,可心和黄瑶分别说出了它的两个特征.
可心:图象与x轴交于点(6,0)。
黄瑶:图象与x轴、y轴围成的三角形的面积是9。
你知道这个一次函数的关系式吗?
1.已知不等式-x+5>3x-3的解集是x<2,则直线y=-x+5与y=3x-3的交点坐标是_________.
2.某单位需要用车,准备和一个体车主 ( http: / / www.21cnjy.com )或一国有出租公司其中的一家签订合同,设汽车每月行驶xkm,应付给个体车主的月租费是y元,付给出租车公司的月租费是y元,y,y分别与x之间的函数关系图象是如图11-3-4所示的两条直线,观察图象,回答下列问题:
(1)每月行驶的路程在什么范围内时,租国有出租车公司的出租车合算?
(2)每月行驶的路程等于多少时,租两家车的费用相同?
(3)如果这个单位估计每月行驶的路程为2300km,那么这个单位租哪家的车合算?
( http: / / www.21cnjy.com )
19·2·3一次函数与二元一次方程(组)
一、警句:一次函数图直线,经过 ( http: / / www.21cnjy.com )(0,b)这个点。
K正左低右边高,越走越高向爬山。
K负左高右边低,越来越低很明显。
二、课前展示:
用画图象的方法解不等式2x+1>3x+4
(1)可将不等式化为-x-3>0,作出直线y=-x-3,然后观察:自变量x取何值时,图象上的点在x轴上方?
或(2)画出直线y=2x+1与y=3x+4,然后观察:对于哪些x的值,直线y=2x+1上的点在直线y=3x+4上相应的点的上方?
学习目标:
1.理解一次函数与二元一次方程(组)的关系。
2.会利用函数图象解二元一次方程组。
3.通过学习了解变量问题利用函数方法的优越性。
四、检查预习情况
1.已知2x-y=1,用含x的代数式表示y,则y= 。
2.方程 2x-y=1的解有 个。
3.(1,1)是否是直线y=2x-1上的一个点?
综合以上几个问题,你能得到哪些启示?通过上述问题的讨论,你认为一次函数与二元一次方程有何关系?
五、小组讨论、合作探究:
探究(一)
1. 3x+5y=8对应的一次函数(以x为自变量)的解析式是 。
2.直线y=-x+上任取一点(x,y)则(x,y)一定是方程3x+5y=8的解吗?为什么?
3.在同一直角坐标系中画出直线y=2x-1与y=-x+的图象,并思考:
(1)它们有交点吗?
(2)交点的坐标与方程组
(3)当自变量x取何值时,函数y=2x-1与y=-x+的值相等?这时的函数值是多少?
展示汇报、质疑答疑:
总结一次函数与二元一次方程(组)的关系。
七、拓展延伸:
1号探测气球从海拔5m处出发, ( http: / / www.21cnjy.com )以1m/min的速度上升,与此同时,2号探测气球从海拔15m处出发,以0.5m/min的速度上升,两个气球都上升了1h.
用式子分别表示两个气球所在的位置的海拔y(单位:m)关于上升时间x(单位:min)的函数关系。
在某时刻两个气球能否位于同一高度?如果能,这时气球上升了多长时间?位于什么高度?
你能用一次函数的图像解释上述(2)问题吗?
八、目标回应:
1、_______________________________________
2、
九、作业:必作题:
1、下面是两种移动电话计费方式 :
方式 一 方式 二
月租费/(元/月) 30 0
本地通话费/(元/min 0.30 0.40
用函数方法解答何时两种计费方式费用相等.
2、在同一坐标系中画出一次函数y1=-x+1与y2=2x-2的图象,并根据图象回答下列问题:
(1)写出直线y1=-x+1与y2=2x-2的交点P的坐标.
(2)直接写出:当x取何值时y1>y2;y1《达标测试》:
已知函数y1=kx-2和y2=-3x+b相交于点A(2,-1)
(1)求k、b的值,在同一坐标系中画出两个函数的图象.
(2)利用图象求出:当x取何值时有:①y1(3)利用图象求出:当x取何值时有:①y1<0且y2<0;②y1>0且y2<0
在同一坐标系中画出一次函数y1=-2x+1与y2=2x-3的图象,并根据图象回答下列问题:
(1)直线y1=-2x+1、y2=2x-3与y轴分别交于点A、B,请写出A、B两点的坐标.
(2)写出直线y1=-2x+1与y2=2x-3的交点P的坐标.
(3)求△PAB的面积.
2x-y=1
3x+5y=8
的解有何关系?
警示语:K正一三负二四,变化趋势记心间。
K正左低右边高,同大同小向爬山。
K负左高右边低,一大另小下山峦。
学习目标
1、理解正比例函数的概念
2、会画正比例函数的图像,理解正比例函数的性质。
四、检查预习情况
按下列要求写出解析式
(1)一本笔记本的单价为2元,现购买x本与付费y元的关系式为_________________;
(2)若正方形的周长为P,边长为a,那么边长a与周长p之间的关系式为______________;
(3)一辆汽车的速度为60 km / h ,则行使路程s与行使时间t之间的关系式为___________;
(4)圆的半径为r,则圆的周长c与半径r之间的关系式为
五、小组讨论、合作探究:
探究(一)
在上述问题中变量之间的对应关系是函数关系吗?如果是,这些函数解析式有哪些共同的特征?
一般地,形如 (k是常数,k≠0)的函数,叫做正比例函数,其中 叫做比例系数。
1、下列函数,那些是正比例函数?______________
(1) (2) (3) (4)
(5) (6) (7)
(8)
2、关于x的函数是正比例函数,则m__________
探究(二)解决下列问题。
画出下列正比例函数的图像
(1)
x -2 -1 0 1 2
(2)
x -2 -1 0 1 2
探究(三)分组合作,交流探索:
比较上面两组图像,填写你发现的规律:
两个图像都是经过原点的 __________,
函数 、 的图像经过第_______象限,从左到右_______,即y随x的增大而________;
函数 、 的图像经过第_______象限,从左到右_______,即y随x的增大而________;
总结:正比例函数的解析式为__________________
相同点
图像所在象限
图像大致形状
增减性
展示汇报、质疑答疑:
因为两点确定一条直线,所以可用两点法画正 ( http: / / www.21cnjy.com )比例函数y=kx(k≠0)图像 。方法:过( )和( )的直线就是
七、拓展延伸:
用你认为最简单的方法画出下列函数的图像。
Y=0.5x y= -2x
七、目标回应:
1、_______________________________________
2、
九、作业:必作题:
1、关于函数,下列结论中,正确的是( )
A、函数图像经过点(1,3) B、函数图像经过二、四象限
C、y随x的增大而增大 D、不论x为何值,总有y>0
2、已知正比例函数的图像过第二、四象限,则( )
A、y随x的增大而增大 B、y随x的增大而减小
C、当时,y随x的增大而增大;当时,y随x的增大而减少;
D、不论x如何变化,y不变。
3、当时,函数的图像在第( )象限。
A、一、三 B、二、四 C、二 D、三
4、函数的图像经过点P(-1,3)则k的值为( )
A、3 B、—3 C、 D、
5、若A(1,m)在函数的图像上,则m=________,则点A关于y轴对称点坐标是___________;
6、若B(m,6)在函数的图像上,则m=________,则点A关于x轴对称点坐标是___________;
达标测试:
1、y与x成正比例,当x=3时,,则y关于x的函数关系式是____________
2、函数的图像在第_______象限,经过点(0,____)与点(1,____),y随x的增大而_________
3、一个函数的图像是经过原点的直线,并且这条直线经过点(1,-3),求这个函数解析式。
19.2.2 一次函数(一)
警示语: K正左低右边高,越走越高向爬山。 ( http: / / www.21cnjy.com )
K负左高右边低,越来越低很明显。
K称斜率b截距,截距为零变正函。
课前展示:
复习什么叫正比例函数,并举例说明。
复习正比例函数的图像和性质。
学习目标:
1、掌握一次函数解析式的特点及意义
2、理解一次函数与正比例函数的关系.
3、会画一次函数的图象
四、检查预习情况
根据题意写出下列函数的解析式
有人发现,在20~25℃时蟋蟀每分鸣叫次数c与温度t(单位:℃)有关,即c的值约是t的7倍与35的差;_______________
一种计算成年人标准体重G(单位:千克)的方法是,以厘米为单位量出身高值h,再减常数105,所得的差是G的值;_______________
某城市的市内电话的月收费为y(单位:元)包括:月租22元,拨打电话x分的计时费(按0.1元/分收取);_______________
把一个长10cm、宽5cm的长方形的长减少xcm,宽不变,长方形的面积y(单位:cm2)随x的值而变化。_______________
五、小组讨论、合作探究:
探究(一)
在上述问题中变量之间的对应关系是函数关系吗?如果是,这些函数解析式有哪些共同的特征?
一般地,形如 (k,b是常数,)的函数,叫做一次函数,特别地,当 时,即,即正比例函数是一种特殊的一次函数。
探究(二)
分组合作;交流探索:
下列函数中,是一次函数的有_____________,是正比例函数的有______________
(1) (2) (3) (4)
(5) (6) (7)
2、若函数是正比例函数,则b = _________
六、展示汇报、质疑答疑:
七、拓展延伸:
1、在一次函数中,k =_______,b =________
2、若函数是一次函数,则m__________
3、在一次函数中,当时,______;当_____时,。
八、目标回应:
1、_______________________________________
2、
九、作业:必作题:
1、下列说法正确的是( )
A、是一次函数 B、一次函数是正比例函数
C、正比例函数是一次函数 D、不是正比例函数就一定不是一次函数
2、仓库内原有粉笔400盒,如果每个星期领 ( http: / / www.21cnjy.com )出36盒,则仓库内余下的粉笔盒数Q与星期数t之间的函数关系式是________________,它是__________函数。
3、随着海拔高度的升高,大 ( http: / / www.21cnjy.com )气压下降,空气的含氧量也随之下降,已知含氧量y与大气压强x成正比例,当x=36时,y=108,请写出y与x的函数解析式___________,这个函数图像在第________象限,同时经过点(0,_____)与点(1,_____)
4.若函数y=(m-1)x+m是关于x的一次函数,试求m的值.
5、下列说法不正确的是( )
(A)一次函数不一定是正比例函数 (B)不是一次函数就一定不是正比例函数
(C)正比例函数是特定的一次函数 (D)不是正比例函数就不是一次函数
6.已知函数y=(2-m)x+2m-3.求当m为何值时,
(1)此函数为正比例函数
(2)此函数为一次函数
.《达标测试》:
一个小球由静止开始在一个斜坡向下滚动,其速度每秒增加2米。
(1)求小球速度v随时间t变化的函数关系式,它是一次函数吗?(2)求第2.5秒时小球的速度?
8、梯形的上底长x,下底长15,高8;
(1)写出梯形的面积y与上底x的关系式,是一次函数吗 ( http: / / www.21cnjy.com )
(2)当x每增加1时, y是如何变化的
(3)当x=0时, y等于多少?此时y的意义是什么
10.若函数y=mx-(4m-4)的图 ( http: / / www.21cnjy.com )象过原点,则m=_______,此时函数是______函数.若函数y=mx-(4m-4)的图象经过(1,3)点,则m=______,此时函数是______函数.
11.在同一坐标系中作出函数Y=2X+3和y=-2x+3的图像。
19.2.2一次函数(二)
警示语:一次函数图直线,经过(0, ( http: / / www.21cnjy.com )b)这个点。
K正左低右边高,越走越高向爬山。
K负左高右边低,越来越低很明显。
K称斜率b截距,截距为零变正函。
课前展示:
一次函数的定义
学习目标:
1.知道一次函数图象的特点,知道一次函数与正比例函数图象之间的关系.。毛
2.理解一次函数图像的性质,了解中的k,b对函数图像的影响
3.会熟练地画一次函数的图象.
四、检查预习情况
在同一个直角坐标系中画出函数,,的图像
-2 -1 0 1 2
y=2x
y=2x+3
y=2x-3
五、小组讨论、合作探究:
探究(一)
分组合作,交流探索:
观察这三个图像,这三个函数图像形状都是________,并且倾斜度_______。函数
的图像经过原点,函数与y轴交于点________,即它可以看作由直线向_____平移_____个单位长度得到;同样的,函数与y轴交于点
________,即它可以看作由直线向_____平移_____个单位长度得到。
探究(二)解决下列问题。
比较一次函数y=kx+b(k≠0)与正比例函数y=kx(k≠0)的解析式与图像你能得到二者的关系吗?
一次函数y=kx+b(k≠0)的图像是一条________,它可以由直线( )平移( )个单位长度得到,当时,它是由直线y=kx(k≠0)向_____平移_____个单位长度得到;当时,它是由直线y=kx(k≠0)向_____平移_____个单位长度得到。
展示汇报、质疑答疑:
在同一个直角坐标系中,把直线向_______平移_____个单位就得到的图像;若向_______平移_____个单位就得到的图像。
将直线向下平移2个单位,可得直线________;
3、将直线向_____平移______个单位可得直线
七、拓展延伸:
1、(1)将直线y=3x向下平移2个单位,得到直线 ;
(2)将直线y=-x-5向上平移5个单位,得到直线 ;
(3)将直线y=-2x+3向下平移5个单位,得到直线 .
2、函数y=kx-4的图象平行于直线y=-2x,求函数的表达式.
八、目标回应:
1、_______________________________________
2、
九、作业:必作题:
1、直线y=kx+b可以看作由直线 ( http: / / www.21cnjy.com )y=kx平移_____个单位而得到,当b>0时,向_____平移,当b<0时,向_____平移。即k值相同时,直线一定平行。
2.在不同坐标系中作出下列函数的图象:
(1)y=3x+2 (2)y= -3x+2 (3)y=3x-2 (4)y= -3x-2
《达标测试》:
一次函数y=kx+b的图象与y轴交于点(0,-2),且与直线平行,求它的函数表达式.
19.2.2一次函数(三)
一、警示语:一次函数图直线,经过(0,b)这 ( http: / / www.21cnjy.com )个点。
K正左低右边高,越走越高向爬山。
K负左高右边低,越来越低很明显。
K称斜率b截距,截距为零变正函。
二、课前展示:
在同坐标系中作出下列函数的图象:
(2)
学习目标:
1、理解一次函数图像的性质,了解中的k,b对函数图像的影响
2.会熟练地画一次函数的图象.
四、检查预习情况
在同坐标系中作出下列函数的图象:
(3) (4)
五、小组讨论、合作探究:
探究(一)
观察上面四个图像,
经过_________象限;y随x的增大而_______,函数的图像从左到右________;
(2)经过_________象限;y随x的增大而_______,函数的图像从左到右________;
(3)经过_________象限;y随x的增大而_______,函数的图像从左到右________;
(4)经过_________象限;y随x的增大而_______,函数的图像从左到右________。
1、由此可以得到直线中, 的取值决定直线的位置:
(1)直线经过___________象限;
(2)直线经过___________象限;
(3)直线经过___________象限;
(4)直线经过___________象限;
2、一次函数的性质:
(1)当时,y随x的增大而_______,这时函数的图像从左到右_______;
(2)当时,y随x的增大而_______,这时函数的图像从左到右_______;
六、展示汇报、质疑答疑:
七、拓展延伸:
1.已知一次函数y=(2m-1)x+m+5,当m是什么数时,函数值y随x的增大而减小?
2.已知一次函数y=(1-2m)x+m-1,若函数y随x的增大而减小,并且函数的图象经过二、三、四象限,求m的取值范围.
八、目标回应:
1、_______________________________________
2、
九、作业:必作题:
选择题:
1、一次函数的图像不经过( )
第一象限 B、第二象限
C、 第三想象限 D、 第四象限
2、已知直线不经过第三象限,也不经过原点,则下列结论正确的是( )
A、 B、
C、 D、
3、下列函数中,y随x的增大而增大的是( )
A、 B、
C、 D、
4、对于一次函数,函数值y随x的增大而减小,则k的取值范围是( )
A、 B、 C、 D、
5、一次函数的图像一定经过( )
A、(3,5) B、(-2,3) C、(2,7) D、(4、10)
6、已知正比例函数的函数值y随x的增大而增大,则一次函数的图像大致是( )
7、一次函数的图像如图所示,则k_______,b_______,y随x的增大而_________
8、一次函数的图像经过___________象限,y随x的增大而_________
《达标测试》:
9、已知点(-1,a)、(2,b)在直线 上,则a,b的大小关系是__________
10、直线与x轴交点坐标为__________;与y轴交点坐标_________;图像经过__________象限,y随x的增大而____________,图像与坐标轴所围成的三角形的面积是___________
11、已知一次函数的图像经过点(0,1),且y随x的增大而增大,请你写出一个符合上述条件的函数关系式_____________
12、已知一次函数图像(1 ( http: / / www.21cnjy.com ))不经过第二象限,(2)经过点(2,-5),请写出一个同时满足(1)和(2)这两个条件的函数关系式:_______________
一、警句:一次函数图直线 ( http: / / www.21cnjy.com ),经过(0,b)这个点。
K正左低右边高,越走越高向爬山。
K负左高右边低,越来越低很明显。
K称斜率b截距,截距为零变正函。
二、课前展示:
复习一次函数的性质及画图像的方法。
学习目标:
1.了解两个条件确定一个一次函数;一个条件确定一个正比例函数.
2.能由两个条件求出一次函数的表达式,一个条件求出正比例函数的表达式.
3能根据函数的图象确定一次函数的表达式,培养学生的数形结合能力.
检查预习情况
一次函数关系式y=kx+b(k≠0),如果知道了k与b的值,函数解析式就确定了,那么有怎样的条件才能求出k和b呢?
已知一次函数的图像经过点(3,5)与(2,3),求这个一次函数的解析式。
分析:求一次函数的解析式,关键是求出k,b的值,从已知条件可以列出关于k,b的二元一次方程组,并求出k,b。
解: ∵一次函数经过点(3,5)与(2,3)
∴
解得
∴一次函数的解析式为_______________
像这样先设出函数解析式,再根据条件确定 ( http: / / www.21cnjy.com )解析式中未知的系数,从而具体写出这个式子的方法,叫做
五、小组讨论、合作探究:
探究(一)
1、已知一次函数,当x = 5时,y = 4,
(1)求这个一次函数。 (2)求当时,函数y的值。
2、.已知一次函数y=kx+b的图象经过点(-1,1)和点(1,-5),求当x=5时,函数y的值.
展示汇报、质疑答疑:
(函数解析式y=kx+b) (满足条件的两个点) 一次函数
(x1 , y1)与(x2 , y2) 的图像
拓展延伸:
黄金一号玉米种子的价格为5元/kg,如果一次购买2kg以上的种子,超过2kg部分的种子价格打8折.
1、完成下表:
购买量/kg 0.5 1 1.5 2 2.5 3 ......
付款金额/元
2、写出购买量关于付款金额的函数解析式,并画出函数的图像。
八、目标回应:
1、_______________________________________
2、
九、作业:必作题:
1、已知弹簧的长度 y(厘米)在一定的 ( http: / / www.21cnjy.com )限度内是所挂重物质量 x(千克)的一次函数.现已测得不挂重物时弹簧的长度是6厘米,挂4千克质量的重物时,弹簧的长度是7.2厘米.求这个一次函数的关系式.
2:已知一次函数的图象如图所示,求出它的函数关系式
3、某自来水公司为了鼓励市民节约用水,采取分段收费标准。居民每月应交水费y(元)是用水量x(吨)的函数,其图象如图所示:
分别写出和时,y与x的函数解析式;
若某用户居民该月用水3.5吨,问应交水费多少元?
若该月交水费9元,则用水多少吨?
《达标测试》:
1、求函数与x轴、y轴的交点坐标,并求这条直线与两坐标轴围成的三角形的面积.
2、某运输公司规定每名旅客行李托运费与所托运行李质量之间的关系式如图所示,请根据图像回答下列问题:
(1)、由图像可知,行李质量只要不超过______kg,就可以免费携带。如果超过了规定的质量,则每超过10kg,要付费_______元。
(2)若旅客携带的行李质量为x(kg),所付的行李费是y(元),请写出y(元)随x(kg)变化的关系式。
(3)若王先生携带行李50kg,他共要付行李费多少元?
19.2.3 一次函数与一元一次方程
警句:一次函数图直线,经过(0,b ( http: / / www.21cnjy.com ))这个点。
K正左低右边高,越走越高向爬山。
K负左高右边低,越来越低很明显。
课前展示:
复习一元一次方程及标准形式的意义。
复习不等式的意义
学习目标:
1、用函数观点认识一元一次方程,认识一元一次不等式与一次函数问题的转化关系.毛
2.学会用图象法求解不等式.
3.进一步理解数形结合思想.
检查预习情况
1、解方程2x+20=0
2.当自变量x为何值时,函数y=2x+20的值为0?
这两个问题之间有什么联系吗?
1.解不等式2x-4>0
2.当自变量x为何值时函数y=2x-4的值大于0?
这两个问题之间有什么联系吗?
五、小组讨论、合作探究:
探究(一)
下面三个方程有什么共同点和不同点?你能从函数的角度对解这三个方程进行解释吗?
(1) 2x+1=3 (2) 2x+1=0 (3)2x+1=-1
结论:
探究(二)
下面三个不等式有什么共同点和不同点?你能从函数的角度对解这三个不等式进行解释吗?
(1) 2x+1>3 (2) 2x+1<0 (3)2x+1<-1
结论:
展示汇报、质疑答疑:
1、若直线y=kx+6与两坐标轴所围成的三角形面积是24,求常数k的值是多少?
分析:(1)一次函数的图象与两条坐标轴围 ( http: / / www.21cnjy.com )成的图形是直角三角形,两条直角边的长分别是图象与x轴的交点的横坐标的绝对值和与y轴的交点的纵坐标的绝对值.
(2)确定图象与两条坐标轴的交点坐标可以通过令x=0和y=0解方程求得.
七、拓展延伸:
2、已知函数y1=kx-2和y2=-3x+b相交于点A(2,-1)
(1)求k、b的值,在同一坐标系中画出两个函数的图象.
(2)利用图象求出:当x取何值时有:①y1
八、目标回应:
1、_______________________________________
2、
九、作业:必作题:
1.直线y=3x+9与x轴的交点是( )
A.(0,-3) B.(-3,0) C.(0,3) D.(0,-3)
2.直线y=kx+3与x轴的交点是(1,0),则k的值是( )
A.3 B.2 C.-2 D.-3
3.已知直线y=kx+b与直线y=3x-1交于y轴同一点,则b的值是( )
A.1 B.-1 C. D.-
4.已知直线AB∥x轴,且点A的坐标是(-1,1),则直线y=x与直线AB的交点是( )
A.(1,1) B.(-1,-1) C.(1,-1) D.(-1,1)
5.直线y=3x+6与x轴的交点的横坐标x的值是方程2x+a=0的解,则a的值是______.
6.已知直线y=2x+8与x轴和y轴 ( http: / / www.21cnjy.com )的交点的坐标分别是_______、_______.与两条坐标轴围成的三角形的面积是__________.
7.已知关于x的方程mx+n=0的解是x=-2,则直线y=mx+n与x轴的交点坐标是________.
8.方程3x+2=8的解是__________,则函数y=3x+2在自变量x等于_________时的函数值是8.
1.直线y=x-1上的点在x轴上方时对应的自变量的范围是( )
A.x>1 B.x≥1 C.x<1 D.x≤1
2.已知直线y=2x+k与x轴的交点为(-2,0),则关于x的不等式2x+k<0的解集是( )
A.x>-2 B.x≥-2 C.x<-2 D.x≤-2
3.已知关于x的不等式ax+1>0(a≠0)的解集是x<1,则直线y=ax+1与x轴的交点是( )
A.(0,1) B.(-1,0) C.(0,-1) D.(1,0)
4.当自变量x的值满足____________时,直线y=-x+2上的点在x轴下方.
5.已知直线y=x-2与y=-x+2相交于点(2,0),则不等式x-2≥-x+2的解集是________.
6.直线y=-3x-3与x轴的交点坐标是________,则不等式-3x+9>12的解集是________.
7.已知关于x的不等式kx-2>0(k≠0)的解集是x>-3,则直线y=-kx+2与x轴的交点是__________.
《达标测试》:
有一个一次函数的图象,可心和黄瑶分别说出了它的两个特征.
可心:图象与x轴交于点(6,0)。
黄瑶:图象与x轴、y轴围成的三角形的面积是9。
你知道这个一次函数的关系式吗?
1.已知不等式-x+5>3x-3的解集是x<2,则直线y=-x+5与y=3x-3的交点坐标是_________.
2.某单位需要用车,准备和一个体车主 ( http: / / www.21cnjy.com )或一国有出租公司其中的一家签订合同,设汽车每月行驶xkm,应付给个体车主的月租费是y元,付给出租车公司的月租费是y元,y,y分别与x之间的函数关系图象是如图11-3-4所示的两条直线,观察图象,回答下列问题:
(1)每月行驶的路程在什么范围内时,租国有出租车公司的出租车合算?
(2)每月行驶的路程等于多少时,租两家车的费用相同?
(3)如果这个单位估计每月行驶的路程为2300km,那么这个单位租哪家的车合算?
( http: / / www.21cnjy.com )
19·2·3一次函数与二元一次方程(组)
一、警句:一次函数图直线,经过 ( http: / / www.21cnjy.com )(0,b)这个点。
K正左低右边高,越走越高向爬山。
K负左高右边低,越来越低很明显。
二、课前展示:
用画图象的方法解不等式2x+1>3x+4
(1)可将不等式化为-x-3>0,作出直线y=-x-3,然后观察:自变量x取何值时,图象上的点在x轴上方?
或(2)画出直线y=2x+1与y=3x+4,然后观察:对于哪些x的值,直线y=2x+1上的点在直线y=3x+4上相应的点的上方?
学习目标:
1.理解一次函数与二元一次方程(组)的关系。
2.会利用函数图象解二元一次方程组。
3.通过学习了解变量问题利用函数方法的优越性。
四、检查预习情况
1.已知2x-y=1,用含x的代数式表示y,则y= 。
2.方程 2x-y=1的解有 个。
3.(1,1)是否是直线y=2x-1上的一个点?
综合以上几个问题,你能得到哪些启示?通过上述问题的讨论,你认为一次函数与二元一次方程有何关系?
五、小组讨论、合作探究:
探究(一)
1. 3x+5y=8对应的一次函数(以x为自变量)的解析式是 。
2.直线y=-x+上任取一点(x,y)则(x,y)一定是方程3x+5y=8的解吗?为什么?
3.在同一直角坐标系中画出直线y=2x-1与y=-x+的图象,并思考:
(1)它们有交点吗?
(2)交点的坐标与方程组
(3)当自变量x取何值时,函数y=2x-1与y=-x+的值相等?这时的函数值是多少?
展示汇报、质疑答疑:
总结一次函数与二元一次方程(组)的关系。
七、拓展延伸:
1号探测气球从海拔5m处出发, ( http: / / www.21cnjy.com )以1m/min的速度上升,与此同时,2号探测气球从海拔15m处出发,以0.5m/min的速度上升,两个气球都上升了1h.
用式子分别表示两个气球所在的位置的海拔y(单位:m)关于上升时间x(单位:min)的函数关系。
在某时刻两个气球能否位于同一高度?如果能,这时气球上升了多长时间?位于什么高度?
你能用一次函数的图像解释上述(2)问题吗?
八、目标回应:
1、_______________________________________
2、
九、作业:必作题:
1、下面是两种移动电话计费方式 :
方式 一 方式 二
月租费/(元/月) 30 0
本地通话费/(元/min 0.30 0.40
用函数方法解答何时两种计费方式费用相等.
2、在同一坐标系中画出一次函数y1=-x+1与y2=2x-2的图象,并根据图象回答下列问题:
(1)写出直线y1=-x+1与y2=2x-2的交点P的坐标.
(2)直接写出:当x取何值时y1>y2;y1
已知函数y1=kx-2和y2=-3x+b相交于点A(2,-1)
(1)求k、b的值,在同一坐标系中画出两个函数的图象.
(2)利用图象求出:当x取何值时有:①y1
在同一坐标系中画出一次函数y1=-2x+1与y2=2x-3的图象,并根据图象回答下列问题:
(1)直线y1=-2x+1、y2=2x-3与y轴分别交于点A、B,请写出A、B两点的坐标.
(2)写出直线y1=-2x+1与y2=2x-3的交点P的坐标.
(3)求△PAB的面积.
2x-y=1
3x+5y=8
的解有何关系?
