9.4 矩形、菱形、正方形同步练习(含答案)
文档属性
| 名称 | 9.4 矩形、菱形、正方形同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 722.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-17 13:06:10 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
9.4矩形、菱形、正方形
学校:___________姓名:___________班级:___________考号:___________
一、单选题
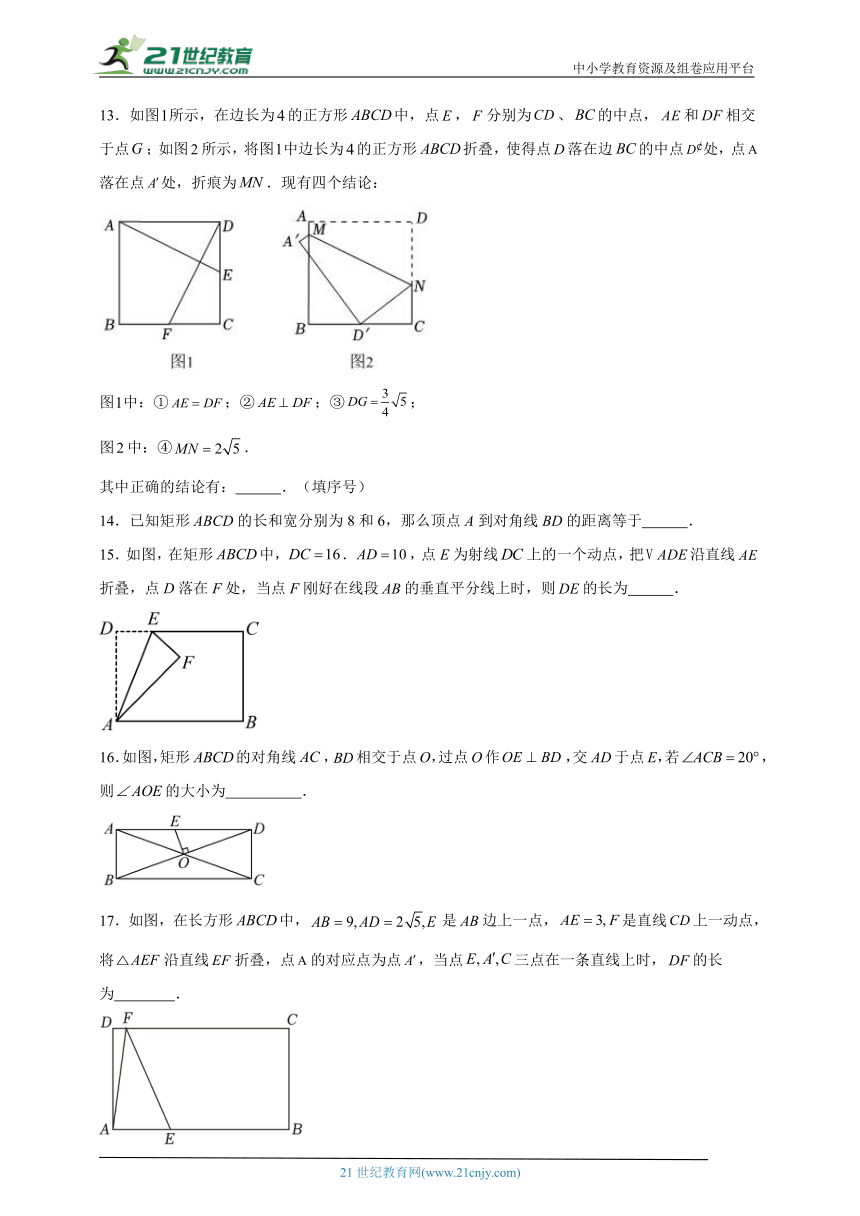
1.“数形结合”思想是数学学习的一个重大思想.通过巧妙运用几何代数的结合性有时能将某些难题迎刃而解.已知a,b,c,d均为实数,a2+b2=c2+d2,则abcd的最大值为( )
A. B. C.1 D.2
2.如图,在平行四边形中,平分,平分,则( )
A. B.四边形是菱形
C.四边形是菱形 D.四边形是矩形
3.如图,矩形ABCD的边,,点E在边上,且,F为边上的一个动点,连接,将线段绕点E顺时针旋转90°得到,连接,则的最小值为( )
A.2 B.3 C. D.
4.如图,点E是正方形外一点,连接和,过点A作垂线交于点P.若.下列结论:①;②;③点B到直线的距高为;④.则正确结论的个数是( )
A.1 B.2 C.3 D.4
5.如图,在四边形ABCD中,AD=BC,点E、F、G、H分别是AB、BD、CD、AC的中点,则对四边形EFGH表述最确切的是( )
A.四边形EFGH是矩形 B.四边形EFGH是菱形
C.四边形EFGH是正方形 D.四边形EFGH是平行四边形
6.一个长方形在平面直角坐标系中三个顶点坐标为(–1,–1)、(–1,2)、(3,–1),则第四个顶点的坐标为( )
A.(3,2) B.(2,3) C.(-2,3) D.(-3,-2)
7.割补法在我国古代数学著作中称为“出入相补”、《九章算术》已经能十分灵活地运用“出入相补”原理解决平面图形的面积问题.在《九章算术》中,三角形被称为圭田.圭田术曰“半广以乘正纵”,也就是说三角形的面积等于底的一半乘高,说明三角形的面积是运用“出入相补”原理,由长方形面积导出的.如图中的三角形下盈上虚,以下补上.如果图中矩形的面积为20,那么图中阴影部分的面积是( ).
A.15 B.10 C.5 D.2.5
8.如图,下列条件中能使成为菱形的是( )
A. B. C. D.
9.如图,在△ABC中,点E 、D、F分别在边AB、BC、CA上,且DE∥AC,DF∥AB.下列说法中错误的是( )
A.四边形AEDF是平行四边形
B.如果∠BAC=90 ,那么四边形AEDF是矩形
C.如果AD⊥BC,那么四边形AEDF是正方形
D.如果AD平分∠BAC,那么四边形AEDF是菱形
10.如图,在矩形ABCD中,AE⊥BD,垂足为E,∠DAE:∠BAE=1:2,则∠CAE的度数( )
A.30° B.45° C.60° D.75°
二、填空题
11.如图,把边长为4的正方形纸片分成五块,其中点为正方形的中心,点,,,分别为,,,的中点.用这五块纸片拼成与此正方形不全等的四边形(要求这五块纸片不重叠无缝隙),则四边形的周长是 .
12.如图,矩形ABCD中,AB=6,BC=8,AE⊥BD于点E则AE之长为 .
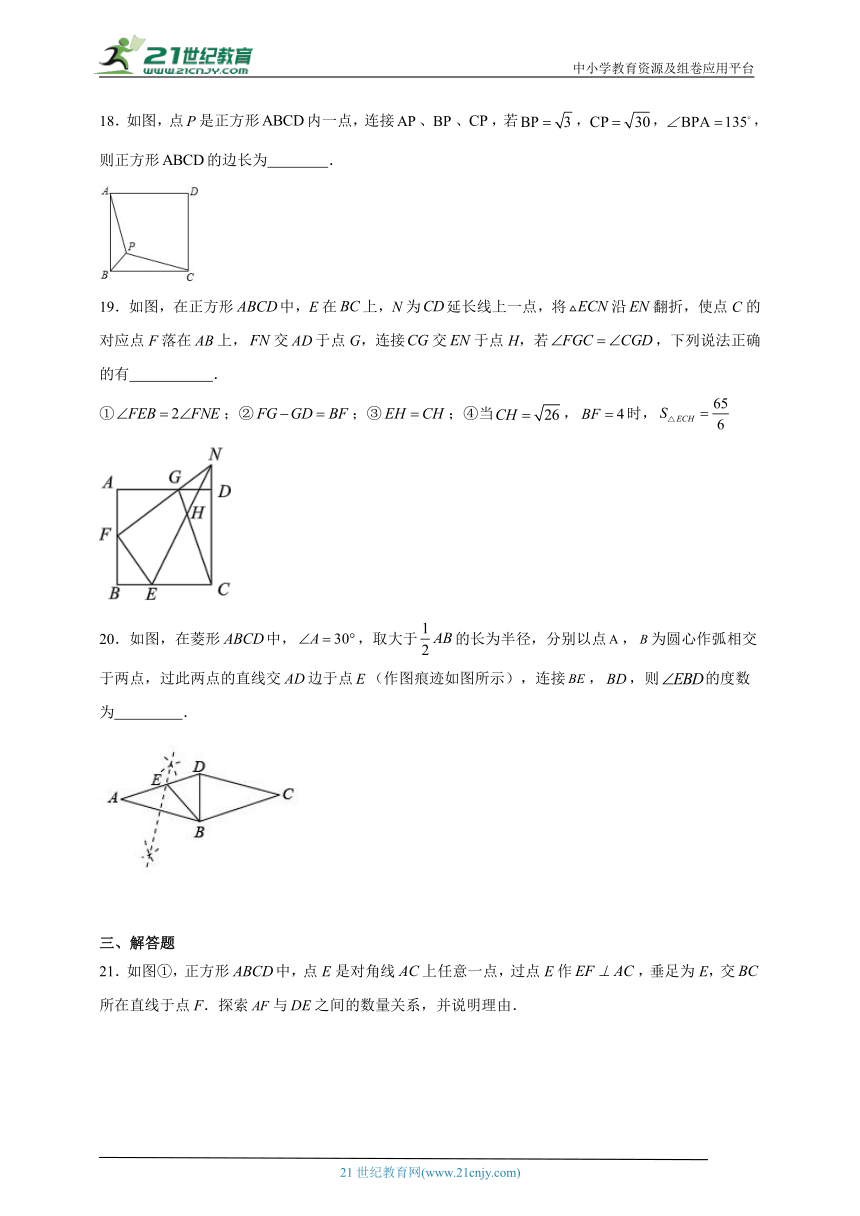
13.如图所示,在边长为的正方形中,点,分别为、的中点,和相交于点;如图所示,将图中边长为的正方形折叠,使得点落在边的中点处,点落在点处,折痕为.现有四个结论:
图中:①;②;③;
图中:④.
其中正确的结论有: .(填序号)
14.已知矩形ABCD的长和宽分别为8和6,那么顶点A到对角线BD的距离等于 .
15.如图,在矩形中,.,点E为射线上的一个动点,把沿直线折叠,点D落在F处,当点F刚好在线段的垂直平分线上时,则的长为 .
16.如图,矩形的对角线,相交于点O,过点O作,交于点E,若,则的大小为 .
17.如图,在长方形中,是边上一点,是直线上一动点,将沿直线折叠,点的对应点为点,当点三点在一条直线上时,的长为 .
18.如图,点是正方形内一点,连接、、,若,,,则正方形的边长为 .
19.如图,在正方形中,E在上,N为延长线上一点,将沿翻折,使点C的对应点F落在上,交于点G,连接交于点H,若,下列说法正确的有 .
①;②;③;④当,时,
20.如图,在菱形中,,取大于的长为半径,分别以点,为圆心作弧相交于两点,过此两点的直线交边于点(作图痕迹如图所示),连接,,则的度数为 .
三、解答题
21.如图①,正方形中,点E是对角线上任意一点,过点E作,垂足为E,交所在直线于点F.探索与之间的数量关系,并说明理由.
(1)如图②,当E是对角线的中点时,与之间的数量关系是 .
(2)小明用“平移法”将沿方向平移得到,将原来分散的两条线段集中到同一个三角形中,如图③,这样就可以将问题转化为探究与之间的数量关系.请你按照他的思路,完成解题过程.
22.在平行四边形ABCD中,∠BAD的平分线交线段BC于点E,交线段DC的延长线于点F,以EC、CF为邻边作平行四边形ECFG.
(1)如图1,证明平行四边形ECFG为菱形;
(2)如图2,若∠ABC=90°,M是EF的中点,求∠BDM的度数;
(3)如图3,若∠ABC=120°,请直接写出∠BDG的度数.
23.在中,,.
(1)如图①,将沿直线BE折叠,使点A的对应点F落在BC边上,求证:四边形ABFE是菱形.
(2)如图②,若是矩形,
①按(1)中操作进行,求证:四边形ABFE是正方形.
②在矩形ABCD中折叠出一个菱形,并使菱形的各个顶点都在矩形的边上,则菱形面积的最大值为______,最小值为______.
24.如图,在矩形ABCD中,E是对角线BD上一点(不与点B、D重合),过点E作EF∥AB,且EF=AB,连接AE、BF、CF.
(1)若DE=DC,求证:四边形CDEF是菱形;
(2)若AB=,BC=3,当四边形ABFE周长最小时,四边形CDEF的周长为 .
25.如图,ABC中,AC的垂直平分线MN交AB于点D,交AC于点O,CE∥AB交MN于E,连接AE、CD.
(1)求证:AD=CE;
(2)试判断四边形ADCE的形状,并说明理由.
参考答案:
1.D
2.B
3.D
4.C
5.B
6.A
7.C
8.D
9.C
10.A
11.20或或或
12.4.8
13.①②④
14.
15.5或20/20或5
16./50度
17.或
18.
19.①②④
20.45°
21.(1)
(2)
22.(1)略;
(2)∠BDM的度数为45°;
(3)∠BDG的度数为60°.
23.(1)略
(2)①略;②,24
24.(1)略;(2)
25.(1)略;(2)菱形
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
9.4矩形、菱形、正方形
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.“数形结合”思想是数学学习的一个重大思想.通过巧妙运用几何代数的结合性有时能将某些难题迎刃而解.已知a,b,c,d均为实数,a2+b2=c2+d2,则abcd的最大值为( )
A. B. C.1 D.2
2.如图,在平行四边形中,平分,平分,则( )
A. B.四边形是菱形
C.四边形是菱形 D.四边形是矩形
3.如图,矩形ABCD的边,,点E在边上,且,F为边上的一个动点,连接,将线段绕点E顺时针旋转90°得到,连接,则的最小值为( )
A.2 B.3 C. D.
4.如图,点E是正方形外一点,连接和,过点A作垂线交于点P.若.下列结论:①;②;③点B到直线的距高为;④.则正确结论的个数是( )
A.1 B.2 C.3 D.4
5.如图,在四边形ABCD中,AD=BC,点E、F、G、H分别是AB、BD、CD、AC的中点,则对四边形EFGH表述最确切的是( )
A.四边形EFGH是矩形 B.四边形EFGH是菱形
C.四边形EFGH是正方形 D.四边形EFGH是平行四边形
6.一个长方形在平面直角坐标系中三个顶点坐标为(–1,–1)、(–1,2)、(3,–1),则第四个顶点的坐标为( )
A.(3,2) B.(2,3) C.(-2,3) D.(-3,-2)
7.割补法在我国古代数学著作中称为“出入相补”、《九章算术》已经能十分灵活地运用“出入相补”原理解决平面图形的面积问题.在《九章算术》中,三角形被称为圭田.圭田术曰“半广以乘正纵”,也就是说三角形的面积等于底的一半乘高,说明三角形的面积是运用“出入相补”原理,由长方形面积导出的.如图中的三角形下盈上虚,以下补上.如果图中矩形的面积为20,那么图中阴影部分的面积是( ).
A.15 B.10 C.5 D.2.5
8.如图,下列条件中能使成为菱形的是( )
A. B. C. D.
9.如图,在△ABC中,点E 、D、F分别在边AB、BC、CA上,且DE∥AC,DF∥AB.下列说法中错误的是( )
A.四边形AEDF是平行四边形
B.如果∠BAC=90 ,那么四边形AEDF是矩形
C.如果AD⊥BC,那么四边形AEDF是正方形
D.如果AD平分∠BAC,那么四边形AEDF是菱形
10.如图,在矩形ABCD中,AE⊥BD,垂足为E,∠DAE:∠BAE=1:2,则∠CAE的度数( )
A.30° B.45° C.60° D.75°
二、填空题
11.如图,把边长为4的正方形纸片分成五块,其中点为正方形的中心,点,,,分别为,,,的中点.用这五块纸片拼成与此正方形不全等的四边形(要求这五块纸片不重叠无缝隙),则四边形的周长是 .
12.如图,矩形ABCD中,AB=6,BC=8,AE⊥BD于点E则AE之长为 .
13.如图所示,在边长为的正方形中,点,分别为、的中点,和相交于点;如图所示,将图中边长为的正方形折叠,使得点落在边的中点处,点落在点处,折痕为.现有四个结论:
图中:①;②;③;
图中:④.
其中正确的结论有: .(填序号)
14.已知矩形ABCD的长和宽分别为8和6,那么顶点A到对角线BD的距离等于 .
15.如图,在矩形中,.,点E为射线上的一个动点,把沿直线折叠,点D落在F处,当点F刚好在线段的垂直平分线上时,则的长为 .
16.如图,矩形的对角线,相交于点O,过点O作,交于点E,若,则的大小为 .
17.如图,在长方形中,是边上一点,是直线上一动点,将沿直线折叠,点的对应点为点,当点三点在一条直线上时,的长为 .
18.如图,点是正方形内一点,连接、、,若,,,则正方形的边长为 .
19.如图,在正方形中,E在上,N为延长线上一点,将沿翻折,使点C的对应点F落在上,交于点G,连接交于点H,若,下列说法正确的有 .
①;②;③;④当,时,
20.如图,在菱形中,,取大于的长为半径,分别以点,为圆心作弧相交于两点,过此两点的直线交边于点(作图痕迹如图所示),连接,,则的度数为 .
三、解答题
21.如图①,正方形中,点E是对角线上任意一点,过点E作,垂足为E,交所在直线于点F.探索与之间的数量关系,并说明理由.
(1)如图②,当E是对角线的中点时,与之间的数量关系是 .
(2)小明用“平移法”将沿方向平移得到,将原来分散的两条线段集中到同一个三角形中,如图③,这样就可以将问题转化为探究与之间的数量关系.请你按照他的思路,完成解题过程.
22.在平行四边形ABCD中,∠BAD的平分线交线段BC于点E,交线段DC的延长线于点F,以EC、CF为邻边作平行四边形ECFG.
(1)如图1,证明平行四边形ECFG为菱形;
(2)如图2,若∠ABC=90°,M是EF的中点,求∠BDM的度数;
(3)如图3,若∠ABC=120°,请直接写出∠BDG的度数.
23.在中,,.
(1)如图①,将沿直线BE折叠,使点A的对应点F落在BC边上,求证:四边形ABFE是菱形.
(2)如图②,若是矩形,
①按(1)中操作进行,求证:四边形ABFE是正方形.
②在矩形ABCD中折叠出一个菱形,并使菱形的各个顶点都在矩形的边上,则菱形面积的最大值为______,最小值为______.
24.如图,在矩形ABCD中,E是对角线BD上一点(不与点B、D重合),过点E作EF∥AB,且EF=AB,连接AE、BF、CF.
(1)若DE=DC,求证:四边形CDEF是菱形;
(2)若AB=,BC=3,当四边形ABFE周长最小时,四边形CDEF的周长为 .
25.如图,ABC中,AC的垂直平分线MN交AB于点D,交AC于点O,CE∥AB交MN于E,连接AE、CD.
(1)求证:AD=CE;
(2)试判断四边形ADCE的形状,并说明理由.
参考答案:
1.D
2.B
3.D
4.C
5.B
6.A
7.C
8.D
9.C
10.A
11.20或或或
12.4.8
13.①②④
14.
15.5或20/20或5
16./50度
17.或
18.
19.①②④
20.45°
21.(1)
(2)
22.(1)略;
(2)∠BDM的度数为45°;
(3)∠BDG的度数为60°.
23.(1)略
(2)①略;②,24
24.(1)略;(2)
25.(1)略;(2)菱形
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
