9.5 三角形的中位线同步练习(含答案)
文档属性
| 名称 | 9.5 三角形的中位线同步练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 724.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-17 13:12:44 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
9.5三角形的中位线
学校:___________姓名:___________班级:___________考号:___________
一、单选题
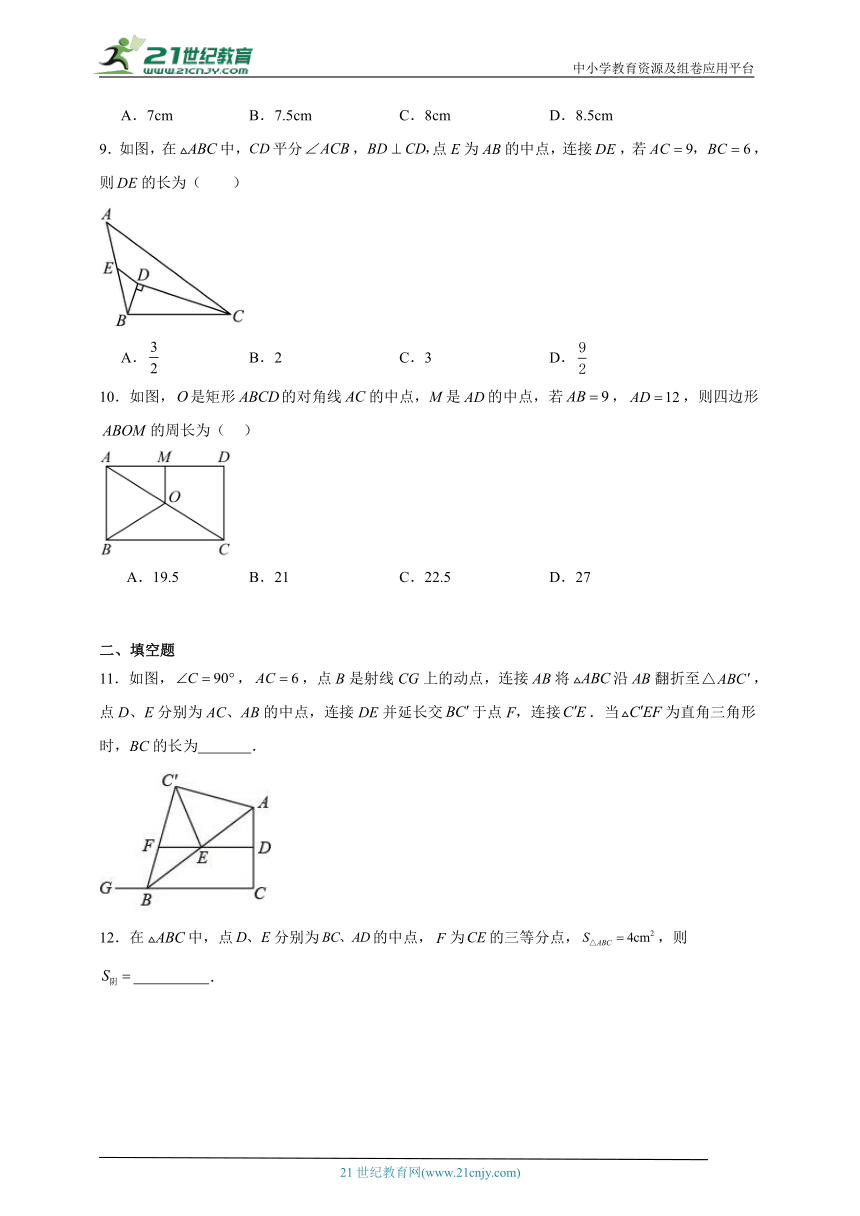
1.如图,四边形中,,分别是,上的点,,分别是,的中点,当点在上从点向移动而点不动时,那么下列结论成立的是( )
A.线段的长逐渐增大 B.线段的长逐渐减小
C.线段的长不变 D.线段的长先逐渐增大后逐渐减小
2.老师布置的作业中有这么一道题:
如图,在中,为的中点,若,.则的长不可能是( ) A.5 B.7 C.8 D.9
甲同学认为,,这条三边不在同一个三角形中,无法解答,老师给的题目有错误.乙同学认为可以从中点出发,构造辅助线,利用全等的知识解决.丙同学认为没必要借助全等三角形的知识,只需构造一个特殊四边形,就可以解决关于三位同学的思考过程,你认为正确的是…( )
A.甲 B.乙 C.丙 D.乙和丙
3.如图,DE垂直平分△ABC的边AB,交CB的延长线于点D,交AB于点E,F是AC的中点,连接AD、EF.若AD=5,CD=9,则EF的长为( )
A.3 B.2.5 C.2 D.1.5
4.如图,是的中位线,点F是的中点,的延长线交于点G,若的面积为2,则的面积为( )
A.18 B.16 C.14 D.12
5.顺次连接下列四边形各边中点,所构成的四边形中为矩形的是( )
A.矩形 B.平行四边形 C.菱形 D.对角线相等且互相平分的四边形
6.四边形ABCD的对角线AC与BD相等且互相垂直,则顺次连接这个四边形四边的中点得到四边形是( )
A.平行四边形 B.矩形 C.菱形 D.正方形
7.一个三角形的三条中位线的长为则此三角形的周长为( )
A. B. C. D.
8.如图,在矩形纸片ABCD中,AB=9cm,BC=12cm,E为边CD上一点,将△BCE沿BE所在的直线折叠,点C恰好落在AD边上的点F处,过点F作FM⊥BE,垂足为点M,取AF的中点N,连接MN,则MN的长为( )
A.7cm B.7.5cm C.8cm D.8.5cm
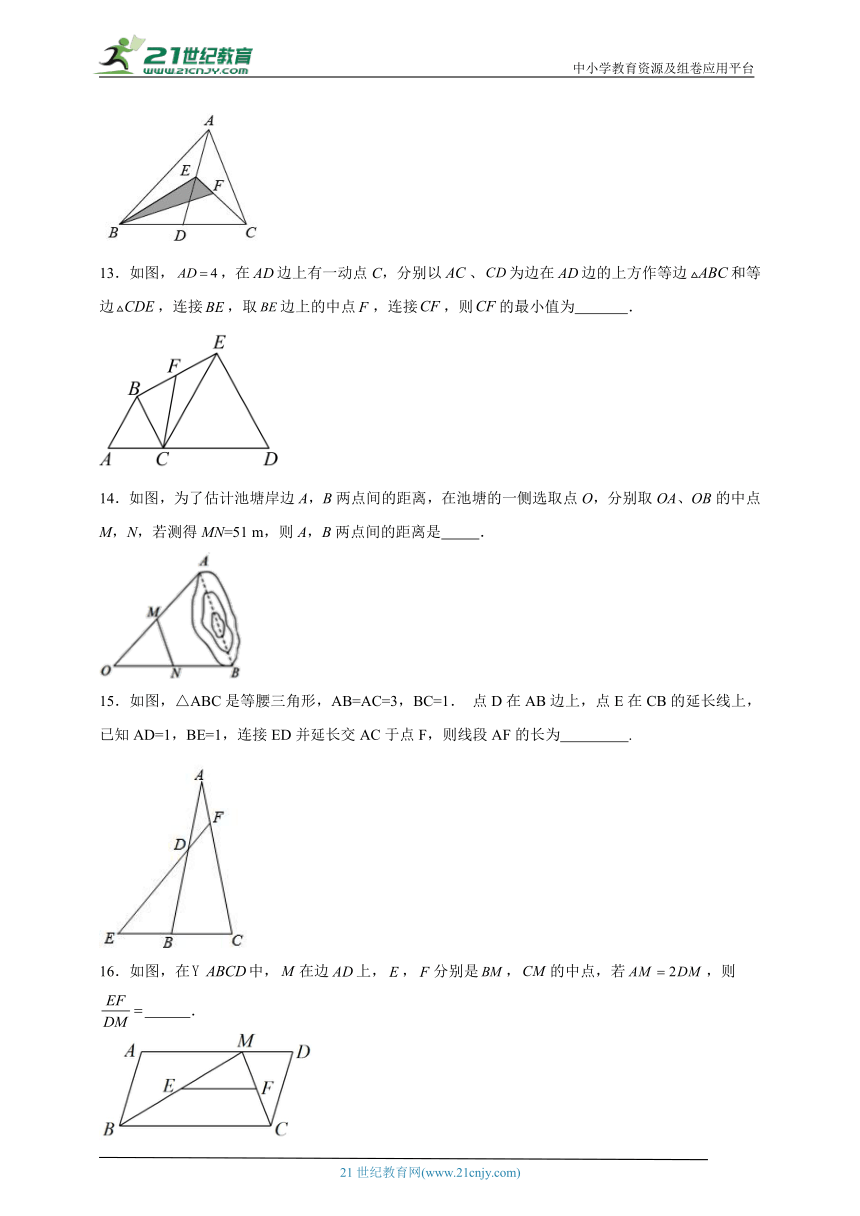
9.如图,在中,平分,点E为的中点,连接,若,则的长为( )
A. B.2 C.3 D.
10.如图,是矩形的对角线的中点,M是的中点,若,,则四边形的周长为( )
A.19.5 B.21 C.22.5 D.27
二、填空题
11.如图,,,点B是射线CG上的动点,连接AB将沿AB翻折至,点D、E分别为AC、AB的中点,连接DE并延长交于点F,连接.当为直角三角形时,BC的长为 .
12.在中,点分别为的中点,为的三等分点,,则 .
13.如图,,在边上有一动点C,分别以、为边在边的上方作等边和等边,连接,取边上的中点,连接,则的最小值为 .
14.如图,为了估计池塘岸边A,B两点间的距离,在池塘的一侧选取点O,分别取OA、OB的中点M,N,若测得MN=51 m,则A,B两点间的距离是 .
15.如图,△ABC是等腰三角形,AB=AC=3,BC=1. 点D在AB边上,点E在CB的延长线上,已知AD=1,BE=1,连接ED并延长交AC于点F,则线段AF的长为 .
16.如图,在中,在边上,,分别是,的中点,若,则 .
17.如图,在中,点D、E分别是边的中点,连接,的平分线交于点F,若,则的长为 .
18.如图,在中,,D,E分别是的中点,F是的中点,若,则 .
19.如图,四边形是菱形,,对角线,相交于点,是边的中点,连接,则的长是 .
20.如图,四边形中,对角线相交于点,、、、分别是、、、的中点,请你添加一个条件 ,使得四边形是菱形.
三、解答题
21.如图,在△ABC 中,∠ABC=90°,在边 AC 上截取 AD=AB,连接 BD,过点 A 作 AE⊥BD 于点E,F 是边 BC 的中点,连接 EF . 若 AB=5,BC=12,求 EF 的长度.
22.如图,在平面直角坐标系中,点B在x轴正半轴上,点A的坐标为(0,6),点P在线段AB上,∠OAB=∠AOP=30°.
(1)求点P的坐标;
(2)将△AOP绕点O顺时针方向旋转,旋转角度为α(0°<α<180°),旋转中的三角形记为△A1OP1(点A、P的对应点分别A1、P1),在旋转过程中,直线OA1交直线AB于点M,直线OP1交直线AB于点N,当△OMN为等腰三角形时,请直接写出α的值.
23.我们已经学行四边形的知识,借助平行四边形的相关性质、判定定理,我们研究学习了三角形的中位线的定义和性质.根据研究图形的规律,请回答以下问题:
(1)三角形中位线定理是:__________________________________________
(2)梯形也是一种常见的四边形,它是有一组对边平行,另一组对边不平行的四边形,连接梯形两腰的中点,得到的线段叫做梯形的中位线.
①请在图中画出梯形的中位线;(请在答题卡上画出此梯形后,画出梯形中位线)
②通过观察、度量、猜想梯形中位线具有的性质并证明.
猜想:梯形的中位线________________.(请在答题卡上把这句话写全)
已知:
求证:
证明:
(3)已知梯形的中位线长6,梯形的高为3,则梯形面积是________________.
参考答案:
1.C
2.D
3.C
4.B
5.C
6.D
7.C
8.B
9.A
10.D
11.6或
12.
13.
14.102m
15.
16.
17.1
18.8
19.1
20.(答案不唯一)
21.4
22.(1)P(,3);(2)当△OMN为等腰三角形时,α的值是45°或90°或135°
23.(1)三角形的中位线平行于第三边,并且等于第三边的一半.
(2)①略;②平行于两底,并且等于两底和的一半;
(3)18
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
9.5三角形的中位线
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,四边形中,,分别是,上的点,,分别是,的中点,当点在上从点向移动而点不动时,那么下列结论成立的是( )
A.线段的长逐渐增大 B.线段的长逐渐减小
C.线段的长不变 D.线段的长先逐渐增大后逐渐减小
2.老师布置的作业中有这么一道题:
如图,在中,为的中点,若,.则的长不可能是( ) A.5 B.7 C.8 D.9
甲同学认为,,这条三边不在同一个三角形中,无法解答,老师给的题目有错误.乙同学认为可以从中点出发,构造辅助线,利用全等的知识解决.丙同学认为没必要借助全等三角形的知识,只需构造一个特殊四边形,就可以解决关于三位同学的思考过程,你认为正确的是…( )
A.甲 B.乙 C.丙 D.乙和丙
3.如图,DE垂直平分△ABC的边AB,交CB的延长线于点D,交AB于点E,F是AC的中点,连接AD、EF.若AD=5,CD=9,则EF的长为( )
A.3 B.2.5 C.2 D.1.5
4.如图,是的中位线,点F是的中点,的延长线交于点G,若的面积为2,则的面积为( )
A.18 B.16 C.14 D.12
5.顺次连接下列四边形各边中点,所构成的四边形中为矩形的是( )
A.矩形 B.平行四边形 C.菱形 D.对角线相等且互相平分的四边形
6.四边形ABCD的对角线AC与BD相等且互相垂直,则顺次连接这个四边形四边的中点得到四边形是( )
A.平行四边形 B.矩形 C.菱形 D.正方形
7.一个三角形的三条中位线的长为则此三角形的周长为( )
A. B. C. D.
8.如图,在矩形纸片ABCD中,AB=9cm,BC=12cm,E为边CD上一点,将△BCE沿BE所在的直线折叠,点C恰好落在AD边上的点F处,过点F作FM⊥BE,垂足为点M,取AF的中点N,连接MN,则MN的长为( )
A.7cm B.7.5cm C.8cm D.8.5cm
9.如图,在中,平分,点E为的中点,连接,若,则的长为( )
A. B.2 C.3 D.
10.如图,是矩形的对角线的中点,M是的中点,若,,则四边形的周长为( )
A.19.5 B.21 C.22.5 D.27
二、填空题
11.如图,,,点B是射线CG上的动点,连接AB将沿AB翻折至,点D、E分别为AC、AB的中点,连接DE并延长交于点F,连接.当为直角三角形时,BC的长为 .
12.在中,点分别为的中点,为的三等分点,,则 .
13.如图,,在边上有一动点C,分别以、为边在边的上方作等边和等边,连接,取边上的中点,连接,则的最小值为 .
14.如图,为了估计池塘岸边A,B两点间的距离,在池塘的一侧选取点O,分别取OA、OB的中点M,N,若测得MN=51 m,则A,B两点间的距离是 .
15.如图,△ABC是等腰三角形,AB=AC=3,BC=1. 点D在AB边上,点E在CB的延长线上,已知AD=1,BE=1,连接ED并延长交AC于点F,则线段AF的长为 .
16.如图,在中,在边上,,分别是,的中点,若,则 .
17.如图,在中,点D、E分别是边的中点,连接,的平分线交于点F,若,则的长为 .
18.如图,在中,,D,E分别是的中点,F是的中点,若,则 .
19.如图,四边形是菱形,,对角线,相交于点,是边的中点,连接,则的长是 .
20.如图,四边形中,对角线相交于点,、、、分别是、、、的中点,请你添加一个条件 ,使得四边形是菱形.
三、解答题
21.如图,在△ABC 中,∠ABC=90°,在边 AC 上截取 AD=AB,连接 BD,过点 A 作 AE⊥BD 于点E,F 是边 BC 的中点,连接 EF . 若 AB=5,BC=12,求 EF 的长度.
22.如图,在平面直角坐标系中,点B在x轴正半轴上,点A的坐标为(0,6),点P在线段AB上,∠OAB=∠AOP=30°.
(1)求点P的坐标;
(2)将△AOP绕点O顺时针方向旋转,旋转角度为α(0°<α<180°),旋转中的三角形记为△A1OP1(点A、P的对应点分别A1、P1),在旋转过程中,直线OA1交直线AB于点M,直线OP1交直线AB于点N,当△OMN为等腰三角形时,请直接写出α的值.
23.我们已经学行四边形的知识,借助平行四边形的相关性质、判定定理,我们研究学习了三角形的中位线的定义和性质.根据研究图形的规律,请回答以下问题:
(1)三角形中位线定理是:__________________________________________
(2)梯形也是一种常见的四边形,它是有一组对边平行,另一组对边不平行的四边形,连接梯形两腰的中点,得到的线段叫做梯形的中位线.
①请在图中画出梯形的中位线;(请在答题卡上画出此梯形后,画出梯形中位线)
②通过观察、度量、猜想梯形中位线具有的性质并证明.
猜想:梯形的中位线________________.(请在答题卡上把这句话写全)
已知:
求证:
证明:
(3)已知梯形的中位线长6,梯形的高为3,则梯形面积是________________.
参考答案:
1.C
2.D
3.C
4.B
5.C
6.D
7.C
8.B
9.A
10.D
11.6或
12.
13.
14.102m
15.
16.
17.1
18.8
19.1
20.(答案不唯一)
21.4
22.(1)P(,3);(2)当△OMN为等腰三角形时,α的值是45°或90°或135°
23.(1)三角形的中位线平行于第三边,并且等于第三边的一半.
(2)①略;②平行于两底,并且等于两底和的一半;
(3)18
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
