人教版八年级数学上册 第十一章 三角形 期末复习单元卷(含解析)
文档属性
| 名称 | 人教版八年级数学上册 第十一章 三角形 期末复习单元卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 456.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-17 15:09:14 | ||
图片预览



文档简介
人教版八年级数学上册 第十一章 三角形 期末复习单元卷
一、单选题
1.用下列一种正多边形,不能用来作平面镶嵌的是( )
A.正三角形 B.正方形 C.正五边形 D.正六边形
2.盖房子时,在窗框未安装好之前,木工师傅常常先在窗框上斜钉一根木条,使其窗框不变形如图所示,这样做的数学依据是( )
A.三角形的稳定性 B.两点之间线段最短
C.两点确定一条直线 D.垂线段最短
3.如图,人字梯中间一般会设计一“拉杆”,以增加使用梯子时的安全性,这样做蕴含的道理是( )
A.三角形具有稳定性 B.三角形内角和等于180°
C.两点之间线段最短 D.同位角相等,两直线平行
4.n边形的边每增加1条,它的内角和就增加( )
A.90° B.180° C.360° D.
5.下列长度的四根木棒中,能与长度分别为1cm和5cm的木棒首尾相接构成三角形的是( ).
A.3cm B.5cm C.6cm D.10cm
6.如图,在 中, 是 上的一点,且 与 的面积相等,则线段 为 的( )
A.高 B.角平分线 C.中线 D.不能确定
7.如图, 三边的中线 的公共点为 ,若 ,则图中阴影部分的面积为( )
A.6 B.4 C.4.5 D.8
8.如图,工人师傅做了一个长方形窗框 ,E,F,G,H分别是四条边上的中点,为了使它稳固,需要在窗框上钉一根木条,这根木条应钉在( )
A.E,H两点之间 B.E,G两点之间
C.F,H两点之间 D.A,B两点之间
9.正方形网格中的交点,我们称之为格点.如图所示的网格图中,每个小正方形的边长都为.现有格点,那么,在网格图中找出格点,使以和格点为顶点的三角形的面积为1.这样的点可找到的个数为( )
A.4 B.5 C.6 D.7
10.如图,线段AB、CD相交于点O,连接AD、CB,和∠BCD的平分线AP和CP相交于点P,则∠P与∠D、∠B之间存在的数量关系为( )
A. B.
C. D.
二、填空题
11.在 中,已知 , ,则 的度数是
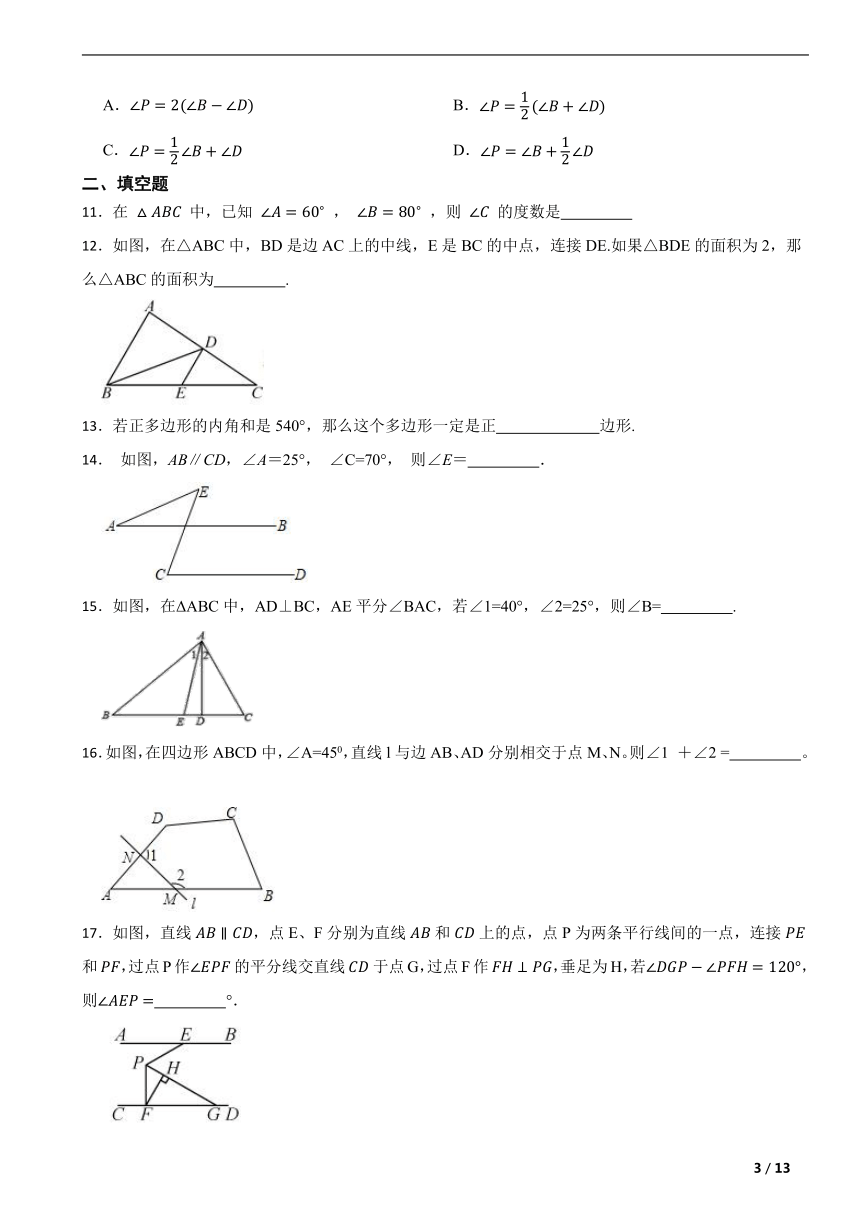
12.如图,在△ABC中,BD是边AC上的中线,E是BC的中点,连接DE.如果△BDE的面积为2,那么△ABC的面积为 .
13.若正多边形的内角和是540°,那么这个多边形一定是正 边形.
14. 如图,AB∥CD,∠A=25°, ∠C=70°, 则∠E= .
15.如图,在ΔABC中,AD⊥BC,AE平分∠BAC,若∠1=40°,∠2=25°,则∠B= .
16.如图,在四边形ABCD中,∠A=450,直线l与边AB、AD分别相交于点M、N。则∠1 +∠2 = 。
17.如图,直线,点E、F分别为直线和上的点,点P为两条平行线间的一点,连接和,过点P作的平分线交直线于点G,过点F作,垂足为H,若,则 °.
三、解答题
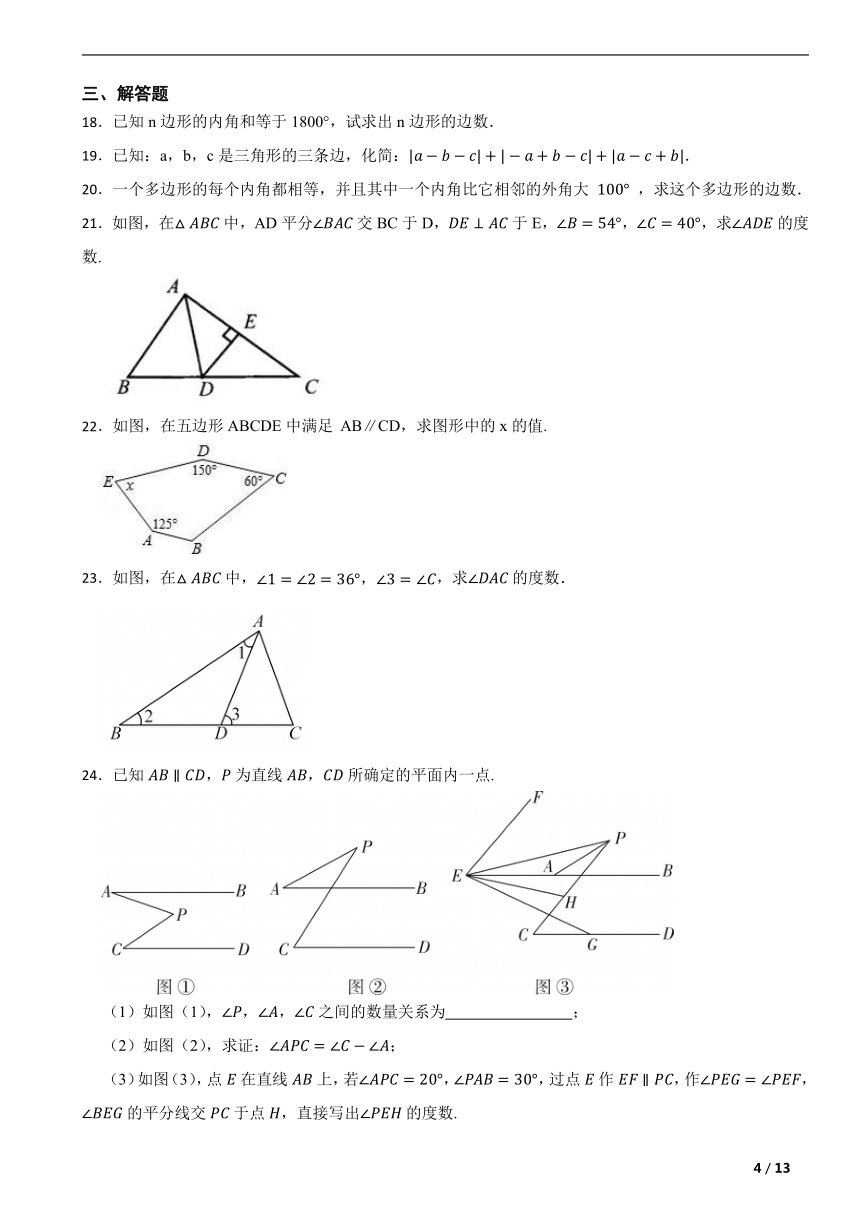
18.已知n边形的内角和等于1800°,试求出n边形的边数.
19.已知:a,b,c是三角形的三条边,化简:.
20.一个多边形的每个内角都相等,并且其中一个内角比它相邻的外角大 ,求这个多边形的边数.
21.如图,在中,AD平分交BC于D,于E,,,求的度数.
22.如图,在五边形ABCDE中满足 AB∥CD,求图形中的x的值.
23.如图,在中,,求的度数.
24.已知,为直线,所确定的平面内一点.
(1)如图(1),,,之间的数量关系为 ;
(2)如图(2),求证:;
(3)如图(3),点在直线上,若,,过点作,作,的平分线交于点,直接写出的度数.
答案解析部分
1.【答案】C
【解析】【解答】解:A、∵360°÷60°=6,∴用6个正三角形能镶嵌成一个平面图形,不符合题意;
B、∵360°÷90°=4,∴用4个正方形能镶嵌成一个平面图形,不符合题意;
C、∵360°÷108°=3……36°,∴用正五边形不能镶嵌成一个平面图形,符合题意;
D、∵360°÷120°=3,∴用3个正六边形能镶嵌成一个平面图形,不符合题意;
只用上面正多边形,不能进行平面镶嵌的是正五边形.
故答案为:C.
【分析】 平面图形镶嵌的条件:判断一种图形是否能够镶嵌,只要看一看拼在同一顶点处的几个角能否构成周角.若能构成360°,则说明能够进行平面镶嵌,反之则不能.
2.【答案】A
【解析】【解答】解:加上木条后,原不稳定的四边形中具有了稳定的三角形,故这种做法根据的是三角形的稳定性.
故答案为:A.
【分析】根据三角形的稳定性求解即可。
3.【答案】A
【解析】【解答】解:∵人字梯中间一般会设计一“拉杆”,
∴构成的是一个三角形,
∴这样做蕴含的道理是三角形具有稳定性.
故答案为:A.
【分析】利用已知条件:人字梯中间一般会设计一“拉杆”,可得到这个图形是一个三角形,因此利用三角形具有稳定性,可求解.
4.【答案】B
【解析】【解答】解:n边形的内角和是(n-2) 180°,
边数增加1,则新的多边形的内角和是(n+1-2) 180°,
则(n+1-2) 180°-(n-2) 180°=180°.
故它的内角和增加180°.
故答案为:B.
【分析】原来的多边形的边数是n,则新的多边形的边数是n+1,根据多边形的内角和定理即可求得.
5.【答案】B
【解析】【解答】解:设第三根木棒的长为x cm,
∵两木棒的长度分别为1cm和5cm,
∴5 1<x<5+1,即4<x<6,
∴只有5cm的木棒符合题意,
故答案为:B.
【分析】根据三角形三边的关系求出第三边的取值范围,再求解即可。
6.【答案】C
【解析】【解答】解:过点A作 于 ,
∵ 与 面积相等,
∴ ,
∴ ,
∴ ,
即线段 一定是 的中线.
故答案为:C.
【分析】过点A作 于 ,由可得,从而得出,根据三角形中线的定义即可判断.
7.【答案】B
【解析】【解答】解:∵AD,BE,CF是△ABC的三条中线,
S△ACF=S△BCF=S△ABC=×12=6;
∴S△AGE=S△CGE=S△ACF=×6=2;
S△BGF=S△BGD=S△BCF=×6=2;
∴S阴影部分=2+2=4.
故答案为:B.
【分析】利用三角形的中线分得的两个三角形的面积相等,就可求出△ACF和△BCF的面积,同时可证得△CGE的面积与△ACF的面积之间的数量关系,△BFG的面积与△BCF的面积之间的数量关系,即可求出△BFG和△CGE的面积;然后求出阴影部分的面积。
8.【答案】A
【解析】【解答】解:A.若钉在E、H两点处则构成了三角形,能固定窗框,故符合题意;
B.若钉在E、G两点处则构成了两个四边形,不能固定窗框,故不符合题意;
C.若钉在F、H两点处则构成了两个四边形,不能固定窗框,故不符合题意;
D.若钉在A、B两点处则未改变形状,不能固定窗框,故不符合题意;
故答案为:A.
【分析】根据三角形的稳定性进行判断逐一判断即可.
9.【答案】C
【解析】【解答】解:如图,根据题意画出图形,这样的点有6个.
故答案为:C
【分析】分别在线段AB的上方和下方分别找到一个点C使△ABC的面积为1,然后再过点C作AB的平行线,平行线与网格点重合的点即为点C,找出所有符合要求的点即可.
10.【答案】B
【解析】【解答】解:在△AOD中:∠D=180°-∠DAO-∠AOD,
在△BOC中:∠B=180°-∠BCO-∠BOC,
∴∠B+∠D=180°-∠DAO-∠AOD+180°-∠BCO-∠BOC=360°-∠DAO-∠BCO-∠AOD-∠BOC,
∵AP、CP分别平分∠DAB和∠BCD,
∴∠DAO=2∠PAO,∠BCO=2∠PCO,
又∠AOD=∠BOC,
∴∠B+∠D=360°-2∠PAO-2∠PCO-2∠AOD=2(180°-∠PAO-∠PCO-∠AOD),
AP、CD的交点标为点E,
在△CPE中,
∠P=180°-∠PCO-∠CEP,
∵∠CEP=∠AOD+∠PAO,
∴∠P=180°-∠PCO-∠PAO-∠AOD,
∴∠P=(∠B+∠D)。
故答案为:B。
【分析】首先根据三角形内角和定理分别得出∠B=180°-∠BCO-∠BOC,∠D=180°-∠DAO-∠AOD,再根据角平分线的定义和对顶角的性质得出∠B+∠D=2(180°-∠PAO-∠PCO-∠AOD),然后在△CPE中,得出∠P=180°-∠PCO-∠CEP,再根据三角形外角的性质,得出∠P=180°-∠PCO-∠PAO-∠AOD,从而得出结论∠P=(∠B+∠D)。
11.【答案】40°
【解析】【解答】因为三角形内角和为180°,已知 , ,那么
故答案为:40°.
【分析】根据三角形内角和为180°可求解.
12.【答案】8
【解析】【解答】∵E是BC的中点,
∴ ,
∵BD是边AC上的中线,
∴ ,
∴ ,
又△BDE的面积为2,
∴△ABC的面积为8;
故答案是:8.
【分析】三角形的中线:连接顶点和对边的中点的线段叫做三角形的中线,三角形的中线平分三角形的面积可得 即可。
13.【答案】正五边形
【解析】【解答】设这个多边形是n边形,则(n﹣2) 180°=540°,解得n=5.故这个多边形一定是正五边形
【分析】直接利用多边形内角和公式(n﹣2) 180°=540°求解即可.
14.【答案】45°
【解析】【解答】解:∵AB∥CD,∠C=70°,
∴∠EFB=∠C=70°,
∵∠A=25°,
∴∠E=∠EFB-∠A=70°-25°=45°.
故答案为:45°.
【分析】由平行线的性质可得∠EFB=∠C=70°,根据三角形外角的性质可得∠E=∠EFB-∠A,据此即可求解.
15.【答案】35°
【解析】【解答】解:∵AE平分∠BAC,
∴∠1=∠EAD+∠2,
∴∠EAD=∠1-∠2=40°-25°=15°
在Rt△ABD中,
∠B=90°-∠BAD=90°-40°-15=35°
故答案为35°
【分析】根据角平分线的定义可得∠1=∠EAD+∠2,据此求出∠EAD=15°,利用直角三角形两锐角互余即可求出结论.
16.【答案】225°
【解析】【解答】如图,∵∠A=45°,∠A+∠ANM+∠AMN=180°
∴∠ANM+∠AMN=180°-∠A=135°
又∵∠1+∠2+∠ANM+∠AMN=360°
∴∠1+∠2=360°-135°=225°
【分析】利用三角形内角和及两个平角算出答案。
17.【答案】30
【解析】【解答】解:如图,过点P作PQ∥AB,
∵AB∥CD,PQ∥AB,
∴PQ∥AB∥CD,
∴∠AEP=∠EPQ,∠CFP=∠FPQ,
∴∠AEP+∠CFP=∠EPQ+∠FPQ=∠EPF,
∵PG平分∠EPF,
∴∠EPF=2∠FPG,
∴∠AEP=2∠FPG-∠CFP,
∵∠DGP-∠PFH=120°,∠DGP=∠FPG+∠PFH+∠HFG,
∴∠HFG=120°-∠FPG,
∵FH⊥PG,
∴∠PFH=90°-∠FPG,
∴∠CFP=180°-∠PFH-∠HFG=2∠PFG-30°,
∴∠AEP=2∠FPG-∠CFP=30°.
故答案为:30.
【分析】过点P作PQ∥AB,由平行于同一直线的两条直线互相平行得PQ∥AB∥CD,由二直线平行,内错角相等得∠AEP=∠EPQ,∠CFP=∠FPQ,结合角平分线的定义得∠AEP=2∠FPG-∠CFP,根据三角形外角相等及已知条件∠DGP-∠PFH=120°,得∠HFG=120°-∠FPG,由垂直的定义及三角形的内角和定理得∠PFH=90°-∠FPG,进而根据平角定义得∠CFP=180°=2∠PFG-30°,从而即可解决此题.
18.【答案】解:由题意得,(n﹣2) 180°=1800°,
解得:n=12.
答:n边形的边数是12.
【解析】【分析】利用多边形内角和公式(n﹣2) 180°即可解得.
19.【答案】解:∵a、b、c是三角形的三边长,
∴a-b-c<0,-a+b-c<0,a-c+b>0,
∴
=
=
=
【解析】【分析】根据三角形三边的关系可得a-b-c<0,-a+b-c<0,a-c+b>0,再去掉绝对值可得,然后去掉括号并合并同类项即可。
20.【答案】解:设每个内角度数为 度,则与它相邻的外角度数为 ,
根据题意可得 ,
解得 .
所以每个外角为 ,
所以这个多边形的边数为 .
答:这个多边形的边数为9.
【解析】【分析】根据内角与相邻外角和为180度、内角比它相邻的外角大 ,构造方程求出外角度数,最后利用外角和 可求边数.
21.【答案】解:∵ , ,
∴ .
∵ 平分 ,
∴ .
∵ ,
∴
∴.
【解析】【分析】首先根据三角形的内角和定理算出∠BAC的度数,再根据角平分线的定义算出∠DAE的度数,由垂直定义得∠AED=90°,最后再根据三角形内角和定理即可算出答案.
22.【答案】解:∵AB∥CD,∠C=60°,
∴∠B=180°﹣60°=120°,
∴(5﹣2)×180°=x+150°+125°+60°+120°,
∴x=85°.
【解析】【分析】由二直线平行,同旁内角互补可得∠B的度数,然后结合多边形的内角和公式进行计算.
23.【答案】解:在中,,
∴,
∴,
∴;
【解析】【分析】根据外角的性质可得∠3=∠1+∠2=72°,则∠3=∠C=72°,然后根据内角和定理进行计算.
24.【答案】(1)
(2)证明:如图,过点作.
∵,
∴
∵,,
∴
∴
∵,
∴.
(3)解:的度数为
【解析】【解答】解:(1) ∠P=∠A+∠C.理由如下:
过点P作PE∥AB,如下图:
∵AB∥CD,
∴PE∥AB∥CD,
∴∠1=∠A,∠2=∠C,
∴∠P=∠1+∠2=∠A+∠C;
(3)∠PEH的度数为25°,
∵∠APC=20°,∠PAB=30°,如图:
∴∠POB=∠APC+∠PAB=50°,
∵EF∥PC,
∴∠FEB=∠POB=50°,
∵∠PEG=∠PEF,∠BEG的平分线交PC于点H,
∴∠GEH=∠BEG,∠PEG=∠FEG,
∴∠PEH=∠PEG ∠GEH=(∠FEG ∠BEG)=∠FEB=25°.
【分析】(1)过点P作AB的平行线,结合平行线的传递性求解;(2)方法一:标出AB与CP的交点,结合三角形的内角和定理求解,方法二:过点P点作AB的平行线求解;(3)由三角形外角的性质,可求出∠1,然后由平行线的性质,求出∠FEB,再利用角平分线的意义,求得∠PEH.
1 / 1
一、单选题
1.用下列一种正多边形,不能用来作平面镶嵌的是( )
A.正三角形 B.正方形 C.正五边形 D.正六边形
2.盖房子时,在窗框未安装好之前,木工师傅常常先在窗框上斜钉一根木条,使其窗框不变形如图所示,这样做的数学依据是( )
A.三角形的稳定性 B.两点之间线段最短
C.两点确定一条直线 D.垂线段最短
3.如图,人字梯中间一般会设计一“拉杆”,以增加使用梯子时的安全性,这样做蕴含的道理是( )
A.三角形具有稳定性 B.三角形内角和等于180°
C.两点之间线段最短 D.同位角相等,两直线平行
4.n边形的边每增加1条,它的内角和就增加( )
A.90° B.180° C.360° D.
5.下列长度的四根木棒中,能与长度分别为1cm和5cm的木棒首尾相接构成三角形的是( ).
A.3cm B.5cm C.6cm D.10cm
6.如图,在 中, 是 上的一点,且 与 的面积相等,则线段 为 的( )
A.高 B.角平分线 C.中线 D.不能确定
7.如图, 三边的中线 的公共点为 ,若 ,则图中阴影部分的面积为( )
A.6 B.4 C.4.5 D.8
8.如图,工人师傅做了一个长方形窗框 ,E,F,G,H分别是四条边上的中点,为了使它稳固,需要在窗框上钉一根木条,这根木条应钉在( )
A.E,H两点之间 B.E,G两点之间
C.F,H两点之间 D.A,B两点之间
9.正方形网格中的交点,我们称之为格点.如图所示的网格图中,每个小正方形的边长都为.现有格点,那么,在网格图中找出格点,使以和格点为顶点的三角形的面积为1.这样的点可找到的个数为( )
A.4 B.5 C.6 D.7
10.如图,线段AB、CD相交于点O,连接AD、CB,和∠BCD的平分线AP和CP相交于点P,则∠P与∠D、∠B之间存在的数量关系为( )
A. B.
C. D.
二、填空题
11.在 中,已知 , ,则 的度数是
12.如图,在△ABC中,BD是边AC上的中线,E是BC的中点,连接DE.如果△BDE的面积为2,那么△ABC的面积为 .
13.若正多边形的内角和是540°,那么这个多边形一定是正 边形.
14. 如图,AB∥CD,∠A=25°, ∠C=70°, 则∠E= .
15.如图,在ΔABC中,AD⊥BC,AE平分∠BAC,若∠1=40°,∠2=25°,则∠B= .
16.如图,在四边形ABCD中,∠A=450,直线l与边AB、AD分别相交于点M、N。则∠1 +∠2 = 。
17.如图,直线,点E、F分别为直线和上的点,点P为两条平行线间的一点,连接和,过点P作的平分线交直线于点G,过点F作,垂足为H,若,则 °.
三、解答题
18.已知n边形的内角和等于1800°,试求出n边形的边数.
19.已知:a,b,c是三角形的三条边,化简:.
20.一个多边形的每个内角都相等,并且其中一个内角比它相邻的外角大 ,求这个多边形的边数.
21.如图,在中,AD平分交BC于D,于E,,,求的度数.
22.如图,在五边形ABCDE中满足 AB∥CD,求图形中的x的值.
23.如图,在中,,求的度数.
24.已知,为直线,所确定的平面内一点.
(1)如图(1),,,之间的数量关系为 ;
(2)如图(2),求证:;
(3)如图(3),点在直线上,若,,过点作,作,的平分线交于点,直接写出的度数.
答案解析部分
1.【答案】C
【解析】【解答】解:A、∵360°÷60°=6,∴用6个正三角形能镶嵌成一个平面图形,不符合题意;
B、∵360°÷90°=4,∴用4个正方形能镶嵌成一个平面图形,不符合题意;
C、∵360°÷108°=3……36°,∴用正五边形不能镶嵌成一个平面图形,符合题意;
D、∵360°÷120°=3,∴用3个正六边形能镶嵌成一个平面图形,不符合题意;
只用上面正多边形,不能进行平面镶嵌的是正五边形.
故答案为:C.
【分析】 平面图形镶嵌的条件:判断一种图形是否能够镶嵌,只要看一看拼在同一顶点处的几个角能否构成周角.若能构成360°,则说明能够进行平面镶嵌,反之则不能.
2.【答案】A
【解析】【解答】解:加上木条后,原不稳定的四边形中具有了稳定的三角形,故这种做法根据的是三角形的稳定性.
故答案为:A.
【分析】根据三角形的稳定性求解即可。
3.【答案】A
【解析】【解答】解:∵人字梯中间一般会设计一“拉杆”,
∴构成的是一个三角形,
∴这样做蕴含的道理是三角形具有稳定性.
故答案为:A.
【分析】利用已知条件:人字梯中间一般会设计一“拉杆”,可得到这个图形是一个三角形,因此利用三角形具有稳定性,可求解.
4.【答案】B
【解析】【解答】解:n边形的内角和是(n-2) 180°,
边数增加1,则新的多边形的内角和是(n+1-2) 180°,
则(n+1-2) 180°-(n-2) 180°=180°.
故它的内角和增加180°.
故答案为:B.
【分析】原来的多边形的边数是n,则新的多边形的边数是n+1,根据多边形的内角和定理即可求得.
5.【答案】B
【解析】【解答】解:设第三根木棒的长为x cm,
∵两木棒的长度分别为1cm和5cm,
∴5 1<x<5+1,即4<x<6,
∴只有5cm的木棒符合题意,
故答案为:B.
【分析】根据三角形三边的关系求出第三边的取值范围,再求解即可。
6.【答案】C
【解析】【解答】解:过点A作 于 ,
∵ 与 面积相等,
∴ ,
∴ ,
∴ ,
即线段 一定是 的中线.
故答案为:C.
【分析】过点A作 于 ,由可得,从而得出,根据三角形中线的定义即可判断.
7.【答案】B
【解析】【解答】解:∵AD,BE,CF是△ABC的三条中线,
S△ACF=S△BCF=S△ABC=×12=6;
∴S△AGE=S△CGE=S△ACF=×6=2;
S△BGF=S△BGD=S△BCF=×6=2;
∴S阴影部分=2+2=4.
故答案为:B.
【分析】利用三角形的中线分得的两个三角形的面积相等,就可求出△ACF和△BCF的面积,同时可证得△CGE的面积与△ACF的面积之间的数量关系,△BFG的面积与△BCF的面积之间的数量关系,即可求出△BFG和△CGE的面积;然后求出阴影部分的面积。
8.【答案】A
【解析】【解答】解:A.若钉在E、H两点处则构成了三角形,能固定窗框,故符合题意;
B.若钉在E、G两点处则构成了两个四边形,不能固定窗框,故不符合题意;
C.若钉在F、H两点处则构成了两个四边形,不能固定窗框,故不符合题意;
D.若钉在A、B两点处则未改变形状,不能固定窗框,故不符合题意;
故答案为:A.
【分析】根据三角形的稳定性进行判断逐一判断即可.
9.【答案】C
【解析】【解答】解:如图,根据题意画出图形,这样的点有6个.
故答案为:C
【分析】分别在线段AB的上方和下方分别找到一个点C使△ABC的面积为1,然后再过点C作AB的平行线,平行线与网格点重合的点即为点C,找出所有符合要求的点即可.
10.【答案】B
【解析】【解答】解:在△AOD中:∠D=180°-∠DAO-∠AOD,
在△BOC中:∠B=180°-∠BCO-∠BOC,
∴∠B+∠D=180°-∠DAO-∠AOD+180°-∠BCO-∠BOC=360°-∠DAO-∠BCO-∠AOD-∠BOC,
∵AP、CP分别平分∠DAB和∠BCD,
∴∠DAO=2∠PAO,∠BCO=2∠PCO,
又∠AOD=∠BOC,
∴∠B+∠D=360°-2∠PAO-2∠PCO-2∠AOD=2(180°-∠PAO-∠PCO-∠AOD),
AP、CD的交点标为点E,
在△CPE中,
∠P=180°-∠PCO-∠CEP,
∵∠CEP=∠AOD+∠PAO,
∴∠P=180°-∠PCO-∠PAO-∠AOD,
∴∠P=(∠B+∠D)。
故答案为:B。
【分析】首先根据三角形内角和定理分别得出∠B=180°-∠BCO-∠BOC,∠D=180°-∠DAO-∠AOD,再根据角平分线的定义和对顶角的性质得出∠B+∠D=2(180°-∠PAO-∠PCO-∠AOD),然后在△CPE中,得出∠P=180°-∠PCO-∠CEP,再根据三角形外角的性质,得出∠P=180°-∠PCO-∠PAO-∠AOD,从而得出结论∠P=(∠B+∠D)。
11.【答案】40°
【解析】【解答】因为三角形内角和为180°,已知 , ,那么
故答案为:40°.
【分析】根据三角形内角和为180°可求解.
12.【答案】8
【解析】【解答】∵E是BC的中点,
∴ ,
∵BD是边AC上的中线,
∴ ,
∴ ,
又△BDE的面积为2,
∴△ABC的面积为8;
故答案是:8.
【分析】三角形的中线:连接顶点和对边的中点的线段叫做三角形的中线,三角形的中线平分三角形的面积可得 即可。
13.【答案】正五边形
【解析】【解答】设这个多边形是n边形,则(n﹣2) 180°=540°,解得n=5.故这个多边形一定是正五边形
【分析】直接利用多边形内角和公式(n﹣2) 180°=540°求解即可.
14.【答案】45°
【解析】【解答】解:∵AB∥CD,∠C=70°,
∴∠EFB=∠C=70°,
∵∠A=25°,
∴∠E=∠EFB-∠A=70°-25°=45°.
故答案为:45°.
【分析】由平行线的性质可得∠EFB=∠C=70°,根据三角形外角的性质可得∠E=∠EFB-∠A,据此即可求解.
15.【答案】35°
【解析】【解答】解:∵AE平分∠BAC,
∴∠1=∠EAD+∠2,
∴∠EAD=∠1-∠2=40°-25°=15°
在Rt△ABD中,
∠B=90°-∠BAD=90°-40°-15=35°
故答案为35°
【分析】根据角平分线的定义可得∠1=∠EAD+∠2,据此求出∠EAD=15°,利用直角三角形两锐角互余即可求出结论.
16.【答案】225°
【解析】【解答】如图,∵∠A=45°,∠A+∠ANM+∠AMN=180°
∴∠ANM+∠AMN=180°-∠A=135°
又∵∠1+∠2+∠ANM+∠AMN=360°
∴∠1+∠2=360°-135°=225°
【分析】利用三角形内角和及两个平角算出答案。
17.【答案】30
【解析】【解答】解:如图,过点P作PQ∥AB,
∵AB∥CD,PQ∥AB,
∴PQ∥AB∥CD,
∴∠AEP=∠EPQ,∠CFP=∠FPQ,
∴∠AEP+∠CFP=∠EPQ+∠FPQ=∠EPF,
∵PG平分∠EPF,
∴∠EPF=2∠FPG,
∴∠AEP=2∠FPG-∠CFP,
∵∠DGP-∠PFH=120°,∠DGP=∠FPG+∠PFH+∠HFG,
∴∠HFG=120°-∠FPG,
∵FH⊥PG,
∴∠PFH=90°-∠FPG,
∴∠CFP=180°-∠PFH-∠HFG=2∠PFG-30°,
∴∠AEP=2∠FPG-∠CFP=30°.
故答案为:30.
【分析】过点P作PQ∥AB,由平行于同一直线的两条直线互相平行得PQ∥AB∥CD,由二直线平行,内错角相等得∠AEP=∠EPQ,∠CFP=∠FPQ,结合角平分线的定义得∠AEP=2∠FPG-∠CFP,根据三角形外角相等及已知条件∠DGP-∠PFH=120°,得∠HFG=120°-∠FPG,由垂直的定义及三角形的内角和定理得∠PFH=90°-∠FPG,进而根据平角定义得∠CFP=180°=2∠PFG-30°,从而即可解决此题.
18.【答案】解:由题意得,(n﹣2) 180°=1800°,
解得:n=12.
答:n边形的边数是12.
【解析】【分析】利用多边形内角和公式(n﹣2) 180°即可解得.
19.【答案】解:∵a、b、c是三角形的三边长,
∴a-b-c<0,-a+b-c<0,a-c+b>0,
∴
=
=
=
【解析】【分析】根据三角形三边的关系可得a-b-c<0,-a+b-c<0,a-c+b>0,再去掉绝对值可得,然后去掉括号并合并同类项即可。
20.【答案】解:设每个内角度数为 度,则与它相邻的外角度数为 ,
根据题意可得 ,
解得 .
所以每个外角为 ,
所以这个多边形的边数为 .
答:这个多边形的边数为9.
【解析】【分析】根据内角与相邻外角和为180度、内角比它相邻的外角大 ,构造方程求出外角度数,最后利用外角和 可求边数.
21.【答案】解:∵ , ,
∴ .
∵ 平分 ,
∴ .
∵ ,
∴
∴.
【解析】【分析】首先根据三角形的内角和定理算出∠BAC的度数,再根据角平分线的定义算出∠DAE的度数,由垂直定义得∠AED=90°,最后再根据三角形内角和定理即可算出答案.
22.【答案】解:∵AB∥CD,∠C=60°,
∴∠B=180°﹣60°=120°,
∴(5﹣2)×180°=x+150°+125°+60°+120°,
∴x=85°.
【解析】【分析】由二直线平行,同旁内角互补可得∠B的度数,然后结合多边形的内角和公式进行计算.
23.【答案】解:在中,,
∴,
∴,
∴;
【解析】【分析】根据外角的性质可得∠3=∠1+∠2=72°,则∠3=∠C=72°,然后根据内角和定理进行计算.
24.【答案】(1)
(2)证明:如图,过点作.
∵,
∴
∵,,
∴
∴
∵,
∴.
(3)解:的度数为
【解析】【解答】解:(1) ∠P=∠A+∠C.理由如下:
过点P作PE∥AB,如下图:
∵AB∥CD,
∴PE∥AB∥CD,
∴∠1=∠A,∠2=∠C,
∴∠P=∠1+∠2=∠A+∠C;
(3)∠PEH的度数为25°,
∵∠APC=20°,∠PAB=30°,如图:
∴∠POB=∠APC+∠PAB=50°,
∵EF∥PC,
∴∠FEB=∠POB=50°,
∵∠PEG=∠PEF,∠BEG的平分线交PC于点H,
∴∠GEH=∠BEG,∠PEG=∠FEG,
∴∠PEH=∠PEG ∠GEH=(∠FEG ∠BEG)=∠FEB=25°.
【分析】(1)过点P作AB的平行线,结合平行线的传递性求解;(2)方法一:标出AB与CP的交点,结合三角形的内角和定理求解,方法二:过点P点作AB的平行线求解;(3)由三角形外角的性质,可求出∠1,然后由平行线的性质,求出∠FEB,再利用角平分线的意义,求得∠PEH.
1 / 1
