1.3 二元一次方程组的应用(第1课时) 课件(共30张PPT)
文档属性
| 名称 | 1.3 二元一次方程组的应用(第1课时) 课件(共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-18 08:42:05 | ||
图片预览










文档简介
1.3 二元一次方程组的应用
第1课时 用二元一次方程组解决
较为简单的实际问题
1.通过实际问题使学生感受二元一次方程组的广泛应用,体会列二元一次方程组是解决某些实际问题的一种有效的数学模型,增强应用意识;
2.能够由题意找出等量关系,列出二元一次方程组并检验所得结果是否符合实际意义.
3.教师引导学生的自主探索,体会把实际问题转化到数学方程问题的数学思想方法,加强知识的综合运用,培养学生分析问题和解决问题的能力.
4.使学生体验数学活动充满探索与创造,体会到经济社会中数学的应用价值,提高学生探索的精神与能力.
【教学重点】
把应用问题转化为数学问题的过程,即对实际问题的数学模型的建立.
【教学难点】
在实践探索中寻找解题方案.
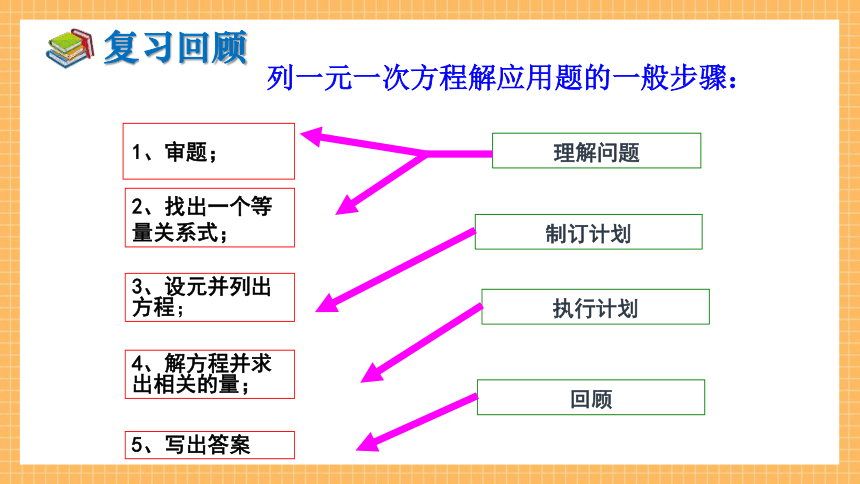
列一元一次方程解应用题的一般步骤:
1、审题;
2、找出一个等量关系式;
3、设元并列出方程;
5、写出答案
4、解方程并求出相关的量;
理解问题
制订计划
执行计划
回顾
《孙子算经》是我国古代一部较为普及的算书,许多问题浅显有趣,其中下卷第 31 题“雉兔同笼”流传尤为广泛,飘洋过海流传到了日本等国.
课本P14 动脑筋:
“鸡兔同笼”是我国古代著名的数学趣题之一. 大约在1500年前成书的《孙子算经》中就有关于“鸡兔同笼”的记载:“今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?” 这四句话的意思是:有若干只鸡兔关在一个笼子里,从上面数,有 35 个头;从下面数,有 94 条腿. 问笼中各有几只鸡和兔?
《孙子算经》中记载的算法:
金鸡独立,兔子站起
94÷2 = 47(只)
1
2
47-35 = 12(只)
脚数:
头数:
35-12 = 23(只)
兔
鸡
1.用我们学过的一元一次方程你能解这个问题吗?
题目意思是:有若干只鸡兔关在一个笼子里,从上面数,有 35 个头;从下面数,有 94 条腿. 问笼中各有几只鸡和兔?
解:设鸡有x只 ,则兔有(35-x)只。
根据题意,得 2????+435?
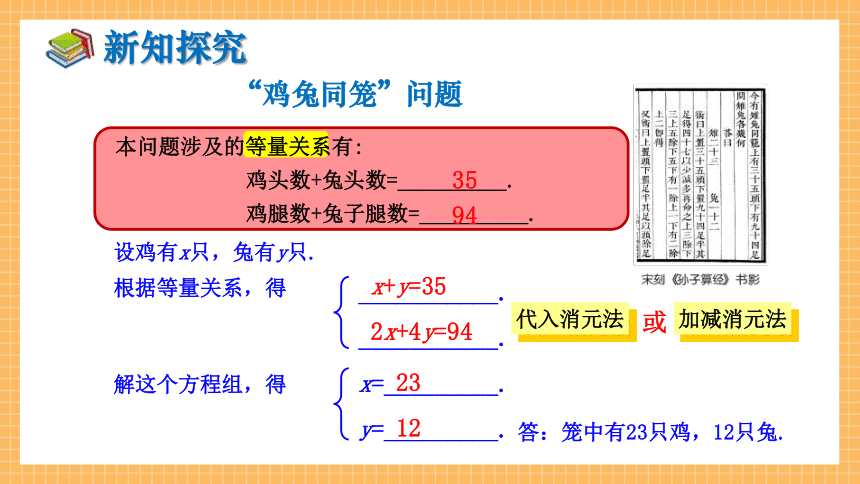
本问题涉及的等量关系有:
鸡头数+兔头数=__________.
鸡腿数+兔子腿数=__________.
35
94
“鸡兔同笼”问题
设鸡有x只,兔有y只.
根据等量关系,得
___________.
___________.
x+y=35
2x+4y=94
解这个方程组,得
x=_________.
y=_________.
23
12
答:笼中有23只鸡,12只兔.
代入消元法
加减消元法
或
列方程解应用题的步骤
1.审题 (找等量关系)
2.设未知数
3.列方程
4.解方程
5.检验,作答
关键:找等量关系、列方程
【例1】某业余运动员针对自行车和长跑项目进行专项训练.
某次训练中,他骑自行车的平均速度为10m/s,跑步的平均
速度为 m/s,自行车路段和长跑路段共5km,共用时15min.求自行车
路段和长跑路段的长度.
分析:本问题涉及的等量关系有:
自行车路段长度+长跑路段长度=总路程,
骑自行车的时间+长跑时间=总时间.
解:设自行车路段的长度为xm,长跑路段的长度为ym.
根据等量关系,得
解这个方程组,得
因此自行车路段长度为3000m,长跑路段的长度为2000m.
解题小结:用二元一次方程组解决实际问题的步骤:
(1) 审题:弄清题意和题目中的_________;
(2) 设元:用___________表示题目中的未知数;
(3) 列方程组:根据___个等量关系列出方程组;
(4) 解方程组:利用__________法或___________解出未知数的值;
(5) 检验并答:检验所求的解是否符合实际意义,然后作答.
数量关系
字母
2
代入消元
加减消元法
?
分析 本题涉及的等量关系有:
金重克数+银重克数=合金重克数,
金重减轻克数+银重减轻克数=合金重减轻克数.
①
②
解:设这块合金中含金 x g,含银 y g.
根据等量关系,得
解这个方程组,得
答:这块合金重含金190克,含银60克.
?
x=190,
y=60.
【例2】某食品厂要配制含蛋白质 15% 的食品 100 kg,现在有含蛋白质分别为 20%,12% 的甲乙两种配料.用这两种配料可以配制出所要求的食品吗?如果可以的话,它们各需多少千克?
分析 本问题涉及的等量关系有:
甲配料质量+乙配料质量 = 总质量,
甲配料含蛋白质质量+乙配料含蛋白质质量= 总蛋白质质量.
解: 设含蛋白质 20% 的配料需用 x kg,含蛋白质
12% 的配料需用 y kg.
根据等量关系得
解这个方程组得
答:可以配制出所要求的食品,其中含蛋白质 20% 的配料需用 37.5 kg,含蛋白质12%的配料需用 62.5 kg.
解:设甲、乙两种商品原来的单价分别为x元,y元,则
x+y=100,
90%x+140%y=120%(x+y),
解得
x=40,
y=60.
答:甲、乙两种商品原来的单价分别为40元、60元.
本问题涉及的等量关系有:
甲的单价+乙的单价=100元,
(1-10%)甲的单价+(1+40%)乙的单价=(1+20%)×100元.
分析
2、甲、乙两种商品原来的单价和为100元,因市场变化,甲商品降价10%,乙商品提价40%,调价后两种商品的单价和比原来的单价和提高了。20%. 求甲、乙两 种商品原来的单价.
3、8 块相同的小长方形地砖拼成一个大长方形,每块小长方形地砖的长和宽分别是多少?(单位 cm)
60cm
x + y = 60,
x = 3y.
解:设小长方形的长为 x,宽为 y,
由题意,得
解此方程组得
x = 45,
y = 15.
答:每块小长方形地砖的长和宽分别是 45 cm,15 cm.
1. 某人买了1分和2分邮票共10张,,共花费12元,设买的两种邮票分别为x张、y张,则下列方程组正确的是( )
D
x+y2=12????+????=10
?
1x+2y=10????+2????=12
?
x+????=5????+2????=10
?
x+????=10????+2????=12
?
A.
B.
C.
D.
2.小亮对小芬说:“我的生日的月和日相加是37,月的2倍和日相加是 43.” 小芬说:“这不可能啊!” 你觉得小芬说得对吗?为什么?
答:对,因为小亮所说的是6月31日,这是不可能的.
本问题涉及的等量关系有:
月+日=37,
月×2+日=43.
分析
解:设月、日分别是x,y,则
x+y=37,
2x+y=43,
x=6,
y=31.
解得
3.学校有许多社团,其中书法社团人数的3倍比绘画社团的人数多15,绘画社团人数的2倍比书法社团的人数多5.设书法社团有x人,绘画社团有????人,下面方程组正确的是( )
A.?????3????=15?????2????=5 B.?????3????=152?????????=5
C.3?????????=15?????2????=5 D.3?????????=152?????????=5
?
D
4. 小洪买了 80 分与 60 分邮票共 17 枚,花了 12.2 元. 试问:80 分与 60 分邮票各买了多少枚?
解:设小洪买 80 分的邮票共 x 枚,买 60 分邮票共 y 枚,
根据题意有
解得
答:小洪买 80 分的邮票共 10 枚,买 60 分的邮票共7 枚.
5.一艘轮船在相距90km的甲、乙两地之间匀速航行,从甲地到乙地顺流航行用6小时,逆流航行用10小时,求该轮船在静水中的速度和水流速度。
解:设该轮船在静水中的速度是每小时x千米,水流速度是每小时y千米。
6????+????=90?????????????
6. 100 匹马恰好拉了 100 片瓦,已知一匹大马能拉 3 片瓦,3 匹小马能拉一片瓦,问有多少匹大马、多少匹小马?
解:设有 x 匹大马, y 匹小马,
由题意,得
解此方程组,得
x = 25,
y = 75.
x + y = 100,
3x + y = 100.
答:有 25 匹大马,75匹小马.
7.小英家今年1月份用水20t,交水费43元;2月份用水18t,交水费38元.该城市实行阶梯水价,14 t以内按正常收费,超出部分则收较高水费.问:在限定量以内的水费每吨多少元?超出部分的水费每吨多少元?
解:设在限定量以内的水费每吨x元,超出部分的水费每吨y元,则
14x+6y=43,
14x+4y=38,
解得
x=2,
y=2.5.
答:在限定量以内的水费每吨2元,超出部分的水费每吨2.5元.
本问题涉及的等量关系有:
1月份14 t以内的水费+1月份超出水费=43元,
2月份14 t以内的水费+2月份超出水费=38元.
分析
8. 某工地挖掘机的台数和装卸机的台数之和为 21,如果每台挖掘机每天平均挖土 750 m3,每台装卸机每天平均运土 300 m3,正好能使挖出的土及时运走,问挖掘机有多少台?装卸机有多少台?
解:设挖掘机 x 台,装卸机 y 台,
根据题意列出方程组得
(以下部分由同学们完成)
9.某水果公司收购某种水果104 t,准备加工后上市销售.该公司加工该种水果的能力是:每天可以精加工4t或粗加工8t.现水果公司计划用16天完成这项加工任务,则应安排几天精加工,几天粗加工?
解:设应安排x天精加工,y天粗加工,则
x+y=16,
4x+8y=104,
解得
x=6,
y=10.
答:应安排6天精加工,10天粗加工.
本问题涉及的等量关系有:
精加工天数+粗加工天数=总天数,
精加工天数×4t+粗加工天数×8t=水果总量.
分析
建立二元一次方程组解决实际问题的步骤如下:
设两个未知数
实际问题
列二元一次
方程组
解方程组
检验解是否
符合实际情况
分析等量关系
习题1.3
第1、2、3、4、5题
第1课时 用二元一次方程组解决
较为简单的实际问题
1.通过实际问题使学生感受二元一次方程组的广泛应用,体会列二元一次方程组是解决某些实际问题的一种有效的数学模型,增强应用意识;
2.能够由题意找出等量关系,列出二元一次方程组并检验所得结果是否符合实际意义.
3.教师引导学生的自主探索,体会把实际问题转化到数学方程问题的数学思想方法,加强知识的综合运用,培养学生分析问题和解决问题的能力.
4.使学生体验数学活动充满探索与创造,体会到经济社会中数学的应用价值,提高学生探索的精神与能力.
【教学重点】
把应用问题转化为数学问题的过程,即对实际问题的数学模型的建立.
【教学难点】
在实践探索中寻找解题方案.
列一元一次方程解应用题的一般步骤:
1、审题;
2、找出一个等量关系式;
3、设元并列出方程;
5、写出答案
4、解方程并求出相关的量;
理解问题
制订计划
执行计划
回顾
《孙子算经》是我国古代一部较为普及的算书,许多问题浅显有趣,其中下卷第 31 题“雉兔同笼”流传尤为广泛,飘洋过海流传到了日本等国.
课本P14 动脑筋:
“鸡兔同笼”是我国古代著名的数学趣题之一. 大约在1500年前成书的《孙子算经》中就有关于“鸡兔同笼”的记载:“今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?” 这四句话的意思是:有若干只鸡兔关在一个笼子里,从上面数,有 35 个头;从下面数,有 94 条腿. 问笼中各有几只鸡和兔?
《孙子算经》中记载的算法:
金鸡独立,兔子站起
94÷2 = 47(只)
1
2
47-35 = 12(只)
脚数:
头数:
35-12 = 23(只)
兔
鸡
1.用我们学过的一元一次方程你能解这个问题吗?
题目意思是:有若干只鸡兔关在一个笼子里,从上面数,有 35 个头;从下面数,有 94 条腿. 问笼中各有几只鸡和兔?
解:设鸡有x只 ,则兔有(35-x)只。
根据题意,得 2????+435?
本问题涉及的等量关系有:
鸡头数+兔头数=__________.
鸡腿数+兔子腿数=__________.
35
94
“鸡兔同笼”问题
设鸡有x只,兔有y只.
根据等量关系,得
___________.
___________.
x+y=35
2x+4y=94
解这个方程组,得
x=_________.
y=_________.
23
12
答:笼中有23只鸡,12只兔.
代入消元法
加减消元法
或
列方程解应用题的步骤
1.审题 (找等量关系)
2.设未知数
3.列方程
4.解方程
5.检验,作答
关键:找等量关系、列方程
【例1】某业余运动员针对自行车和长跑项目进行专项训练.
某次训练中,他骑自行车的平均速度为10m/s,跑步的平均
速度为 m/s,自行车路段和长跑路段共5km,共用时15min.求自行车
路段和长跑路段的长度.
分析:本问题涉及的等量关系有:
自行车路段长度+长跑路段长度=总路程,
骑自行车的时间+长跑时间=总时间.
解:设自行车路段的长度为xm,长跑路段的长度为ym.
根据等量关系,得
解这个方程组,得
因此自行车路段长度为3000m,长跑路段的长度为2000m.
解题小结:用二元一次方程组解决实际问题的步骤:
(1) 审题:弄清题意和题目中的_________;
(2) 设元:用___________表示题目中的未知数;
(3) 列方程组:根据___个等量关系列出方程组;
(4) 解方程组:利用__________法或___________解出未知数的值;
(5) 检验并答:检验所求的解是否符合实际意义,然后作答.
数量关系
字母
2
代入消元
加减消元法
?
分析 本题涉及的等量关系有:
金重克数+银重克数=合金重克数,
金重减轻克数+银重减轻克数=合金重减轻克数.
①
②
解:设这块合金中含金 x g,含银 y g.
根据等量关系,得
解这个方程组,得
答:这块合金重含金190克,含银60克.
?
x=190,
y=60.
【例2】某食品厂要配制含蛋白质 15% 的食品 100 kg,现在有含蛋白质分别为 20%,12% 的甲乙两种配料.用这两种配料可以配制出所要求的食品吗?如果可以的话,它们各需多少千克?
分析 本问题涉及的等量关系有:
甲配料质量+乙配料质量 = 总质量,
甲配料含蛋白质质量+乙配料含蛋白质质量= 总蛋白质质量.
解: 设含蛋白质 20% 的配料需用 x kg,含蛋白质
12% 的配料需用 y kg.
根据等量关系得
解这个方程组得
答:可以配制出所要求的食品,其中含蛋白质 20% 的配料需用 37.5 kg,含蛋白质12%的配料需用 62.5 kg.
解:设甲、乙两种商品原来的单价分别为x元,y元,则
x+y=100,
90%x+140%y=120%(x+y),
解得
x=40,
y=60.
答:甲、乙两种商品原来的单价分别为40元、60元.
本问题涉及的等量关系有:
甲的单价+乙的单价=100元,
(1-10%)甲的单价+(1+40%)乙的单价=(1+20%)×100元.
分析
2、甲、乙两种商品原来的单价和为100元,因市场变化,甲商品降价10%,乙商品提价40%,调价后两种商品的单价和比原来的单价和提高了。20%. 求甲、乙两 种商品原来的单价.
3、8 块相同的小长方形地砖拼成一个大长方形,每块小长方形地砖的长和宽分别是多少?(单位 cm)
60cm
x + y = 60,
x = 3y.
解:设小长方形的长为 x,宽为 y,
由题意,得
解此方程组得
x = 45,
y = 15.
答:每块小长方形地砖的长和宽分别是 45 cm,15 cm.
1. 某人买了1分和2分邮票共10张,,共花费12元,设买的两种邮票分别为x张、y张,则下列方程组正确的是( )
D
x+y2=12????+????=10
?
1x+2y=10????+2????=12
?
x+????=5????+2????=10
?
x+????=10????+2????=12
?
A.
B.
C.
D.
2.小亮对小芬说:“我的生日的月和日相加是37,月的2倍和日相加是 43.” 小芬说:“这不可能啊!” 你觉得小芬说得对吗?为什么?
答:对,因为小亮所说的是6月31日,这是不可能的.
本问题涉及的等量关系有:
月+日=37,
月×2+日=43.
分析
解:设月、日分别是x,y,则
x+y=37,
2x+y=43,
x=6,
y=31.
解得
3.学校有许多社团,其中书法社团人数的3倍比绘画社团的人数多15,绘画社团人数的2倍比书法社团的人数多5.设书法社团有x人,绘画社团有????人,下面方程组正确的是( )
A.?????3????=15?????2????=5 B.?????3????=152?????????=5
C.3?????????=15?????2????=5 D.3?????????=152?????????=5
?
D
4. 小洪买了 80 分与 60 分邮票共 17 枚,花了 12.2 元. 试问:80 分与 60 分邮票各买了多少枚?
解:设小洪买 80 分的邮票共 x 枚,买 60 分邮票共 y 枚,
根据题意有
解得
答:小洪买 80 分的邮票共 10 枚,买 60 分的邮票共7 枚.
5.一艘轮船在相距90km的甲、乙两地之间匀速航行,从甲地到乙地顺流航行用6小时,逆流航行用10小时,求该轮船在静水中的速度和水流速度。
解:设该轮船在静水中的速度是每小时x千米,水流速度是每小时y千米。
6????+????=90?????????????
6. 100 匹马恰好拉了 100 片瓦,已知一匹大马能拉 3 片瓦,3 匹小马能拉一片瓦,问有多少匹大马、多少匹小马?
解:设有 x 匹大马, y 匹小马,
由题意,得
解此方程组,得
x = 25,
y = 75.
x + y = 100,
3x + y = 100.
答:有 25 匹大马,75匹小马.
7.小英家今年1月份用水20t,交水费43元;2月份用水18t,交水费38元.该城市实行阶梯水价,14 t以内按正常收费,超出部分则收较高水费.问:在限定量以内的水费每吨多少元?超出部分的水费每吨多少元?
解:设在限定量以内的水费每吨x元,超出部分的水费每吨y元,则
14x+6y=43,
14x+4y=38,
解得
x=2,
y=2.5.
答:在限定量以内的水费每吨2元,超出部分的水费每吨2.5元.
本问题涉及的等量关系有:
1月份14 t以内的水费+1月份超出水费=43元,
2月份14 t以内的水费+2月份超出水费=38元.
分析
8. 某工地挖掘机的台数和装卸机的台数之和为 21,如果每台挖掘机每天平均挖土 750 m3,每台装卸机每天平均运土 300 m3,正好能使挖出的土及时运走,问挖掘机有多少台?装卸机有多少台?
解:设挖掘机 x 台,装卸机 y 台,
根据题意列出方程组得
(以下部分由同学们完成)
9.某水果公司收购某种水果104 t,准备加工后上市销售.该公司加工该种水果的能力是:每天可以精加工4t或粗加工8t.现水果公司计划用16天完成这项加工任务,则应安排几天精加工,几天粗加工?
解:设应安排x天精加工,y天粗加工,则
x+y=16,
4x+8y=104,
解得
x=6,
y=10.
答:应安排6天精加工,10天粗加工.
本问题涉及的等量关系有:
精加工天数+粗加工天数=总天数,
精加工天数×4t+粗加工天数×8t=水果总量.
分析
建立二元一次方程组解决实际问题的步骤如下:
设两个未知数
实际问题
列二元一次
方程组
解方程组
检验解是否
符合实际情况
分析等量关系
习题1.3
第1、2、3、4、5题
