期末图形计算专项:长方体和正方体-数学六年级上册苏教版(含解析)
文档属性
| 名称 | 期末图形计算专项:长方体和正方体-数学六年级上册苏教版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 443.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-16 18:43:11 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
期末图形计算专项:长方体和正方体-数学六年级上册苏教版
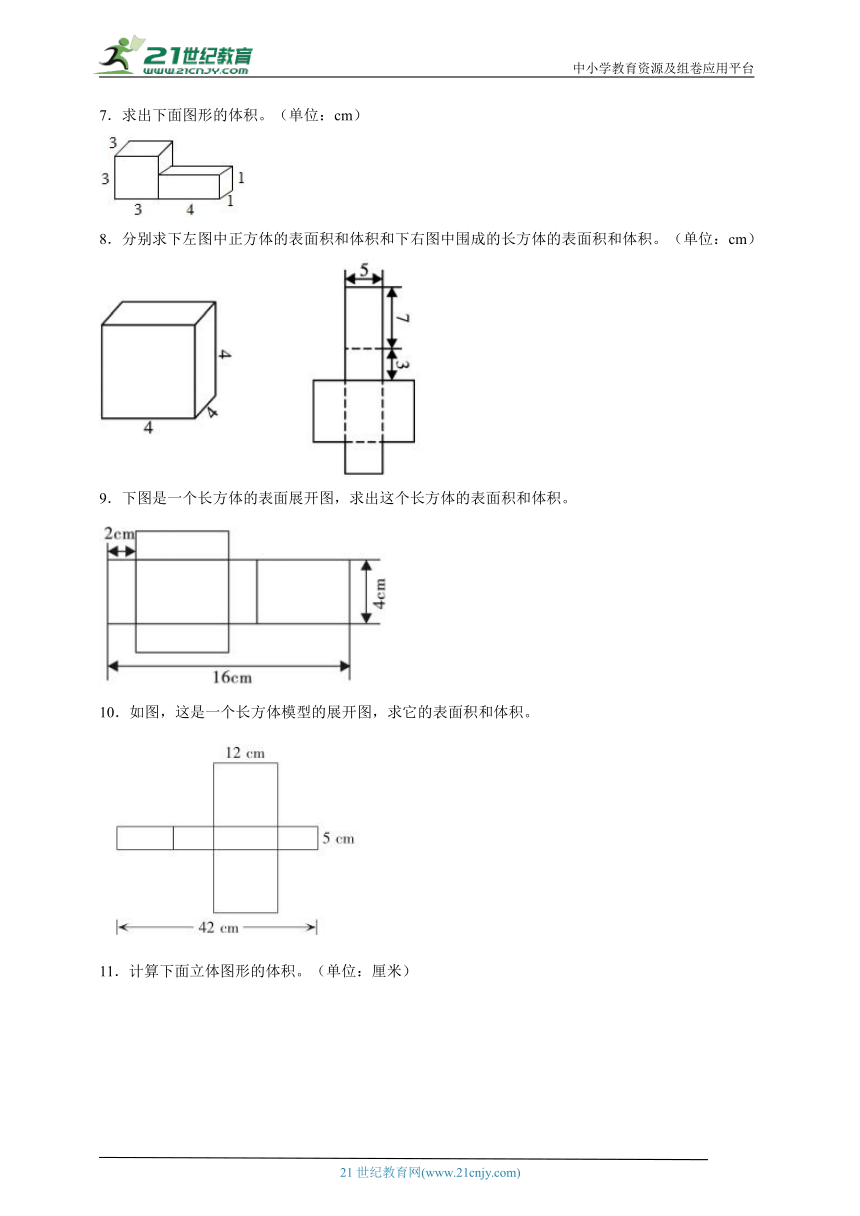
1.计算下面的体积。
2.计算图形的表面积和体积。(单位:分米)
3.下图中长方体长8厘米、宽6厘米、高4厘米,正方体的棱长是5厘米。请计算组合体的表面积和体积。
4.计算下面图形的表面积和体积。(单位:m)
5.计算下面几何体的表面积和体积。
6.求下面图形的表面积和体积。(单位:厘米)
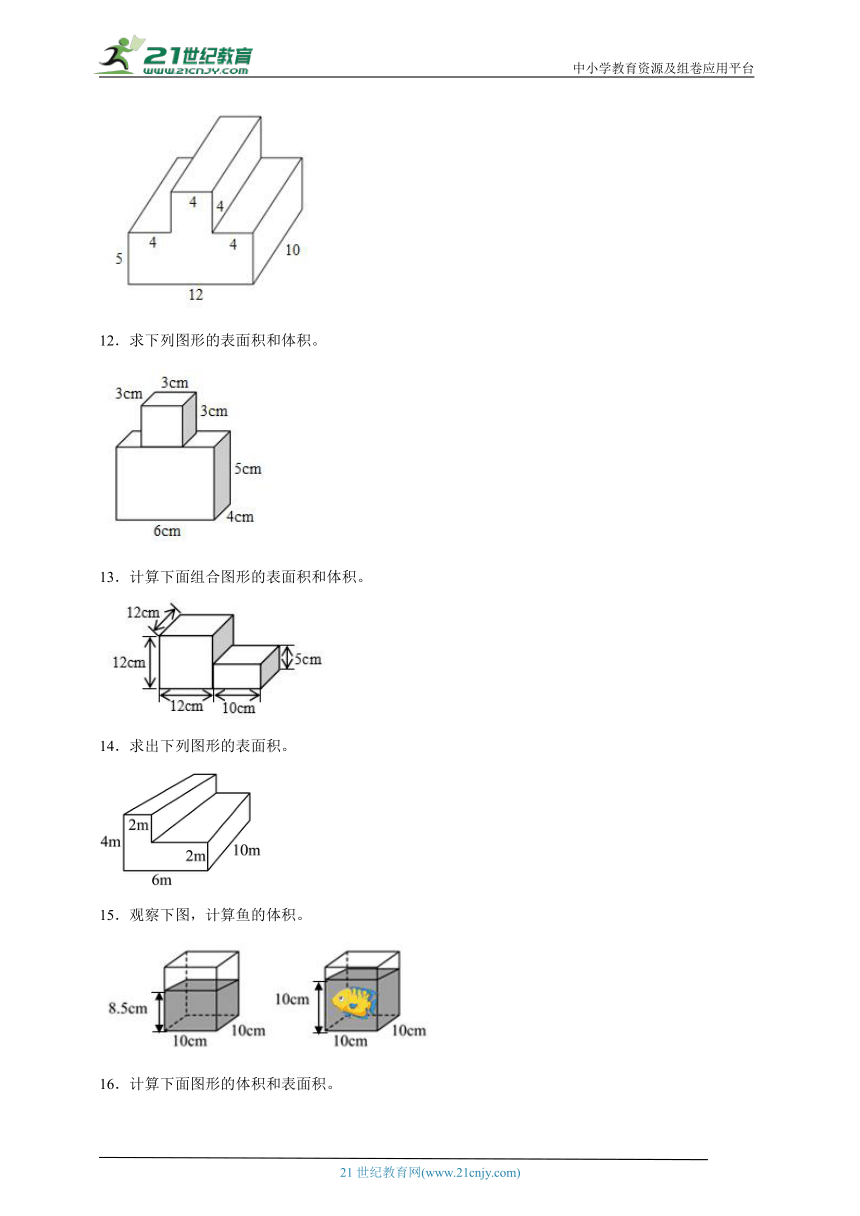
7.求出下面图形的体积。(单位:cm)
8.分别求下左图中正方体的表面积和体积和下右图中围成的长方体的表面积和体积。(单位:cm)
9.下图是一个长方体的表面展开图,求出这个长方体的表面积和体积。
10.如图,这是一个长方体模型的展开图,求它的表面积和体积。
11.计算下面立体图形的体积。(单位:厘米)
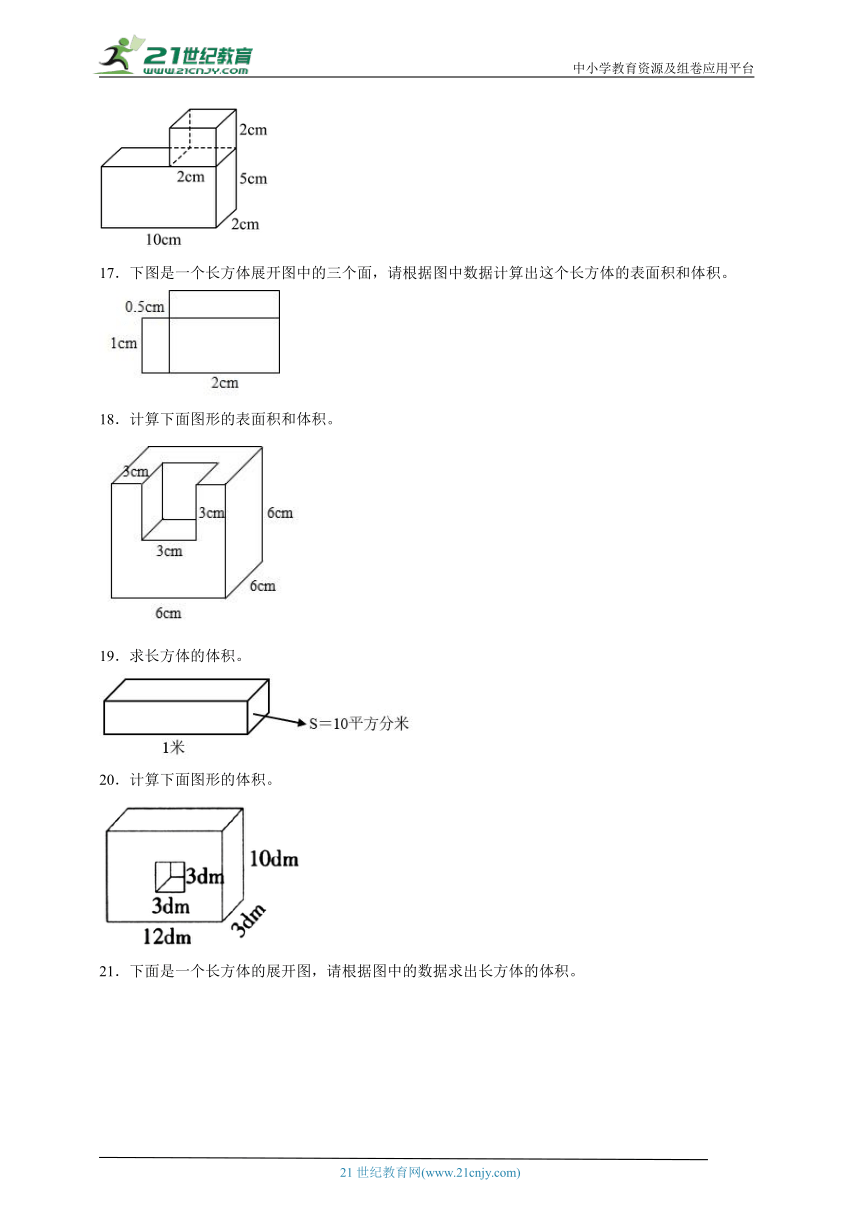
12.求下列图形的表面积和体积。
13.计算下面组合图形的表面积和体积。
14.求出下列图形的表面积。
15.观察下图,计算鱼的体积。
16.计算下面图形的体积和表面积。
17.下图是一个长方体展开图中的三个面,请根据图中数据计算出这个长方体的表面积和体积。
18.计算下面图形的表面积和体积。
19.求长方体的体积。
20.计算下面图形的体积。
21.下面是一个长方体的展开图,请根据图中的数据求出长方体的体积。
参考答案:
1.84cm3;216dm3
【分析】根据长方体体积公式,用7×3×4即可求出长方体的体积;
根据正方体的体积公式,用6×6×6即可求出正方体的体积。
【详解】7×3×4
=21×4
=84(cm3)
长方体的体积是84cm3。
6×6×6
=36×6
=216(dm3)
正方体的体积是216dm3。
2.184平方分米;160立方分米;37.5平方分米;15.625立方分米
【分析】根据长方体的表面积公式,用(8×4+8×5+4×5)×2即可求出长方体的表面积;
根据长方体的体积公式,用8×5×4即可求出长方体的体积;
根据正方体的表面积公式,用2.5×2.5×6即可求出正方体的表面积;
根据正方体的体积公式,用2.5×2.5×2.5即可求出正方体的体积。
【详解】(8×4+8×5+4×5)×2
=(32+40+20)×2
=92×2
=184(平方分米)
长方体的表面积是184平方分米。
8×5×4
=40×4
=160(立方分米)
长方体的体积是160立方分米。
2.5×2.5×6
=6.25×6
=37.5(平方分米)
正方体的表面积是37.5平方分米。
2.5×2.5×2.5
=6.25×2.5
=15.625(立方分米)
正方体的体积是15.625立方分米。
3.308平方厘米;317立方厘米
【分析】组合体的表面积=完整的长方体表面积+正方体4个面的面积和,长方体表面积=(长×宽+长×高+宽×高)×2;组合体的体积=长方体体积+正方体体积,长方体体积=长×宽×高,正方体体积=棱长×棱长×棱长,据此列式计算。
【详解】(8×6+8×4+6×4)×2+5×5×4
=(48+32+24)×2+100
=104×2+100
=208+100
=308(平方厘米)
8×6×4+5×5×5
=192+125
=317(立方厘米)
4.表面积428m2;体积453m3
【分析】观察图形可知,在长方体上面挖出一个正方体,长方体的表面积增加了正方体的4个侧面面积。长方体的表面积=(长×宽+长×高+宽×高)×2,正方体4个侧面面积=棱长×棱长×4,据此代入数据计算,再把它们加起来即可。
用长方体的体积减去正方体的体积即是这个图形的体积。长方体的体积=长×宽×高,正方体的体积=棱长×棱长×棱长,据此解答。
【详解】表面积:(12×8+12×5+8×5)×2+3×3×4
=(96+60+40)×2+36
=196×2+36
=392+36
=428(m2)
体积:12×8×5-3×3×3
=480-27
=453(m3)
5.1220m2;2445m3
【分析】长方体的表面积=(长×宽+宽×高+长×高)×2,长方体的体积=长×宽×高,几何体的表面积=大长方体的表面积+小长方体4个侧面的面积,几何体的体积=大长方体的体积+小长方体的体积,据此解答。
【详解】表面积:(20×8+20×15+8×15)×2+5×3×4
=(160+300+120)×2+5×3×4
=580×2+5×3×4
=1160+60
=1220(m2)
体积:20×8×15+5×3×3
=160×15+15×3
=2400+45
=2445(m3)
所以,这个几何体的表面积是1220m2,体积是2445m3。
6.216平方厘米;204立方厘米
【分析】组合体的表面积=大正方体表面积,正方体表面积=棱长×棱长×6;组合体体积=大正方体体积-小长方体体积,正方体体积=棱长×棱长×棱长,长方体体积=棱长×棱长×棱长,据此列式计算。
【详解】(平方厘米)
(立方厘米)
7.31cm3
【分析】组合图形的体积=正方体的体积+长方体的体积;根据正方体的体积=棱长×棱长×棱长,长方体的体积=长×宽×高,代入数据计算即可。
【详解】3×3×3+4×1×1
=27+4
=31(cm3)
图形的体积是31cm3。
8.左图正方体:表面积是96平方厘米;体积是64立方厘米
右图长方体:表面积是142平方厘米;体积是105立方厘米
【分析】正方体的表面积=棱长×棱长×6,正方体的体积=棱长×棱长×棱长,由此代入数据即可解答;长方体的表面积=(长×宽+长×高+宽×高)×2,长方体的体积=长×宽×高
【详解】正方体的表面积是:
4×4×6
=16×6
=96(平方厘米)
体积是:
4×4×4
=16×4
=64(立方厘米)
长方体的表面积是:
(7×5+5×3+7×3)×2
=(35+15+21)×2
=71×2
=142(平方厘米)
体积是:
7×5×3
=35×3
=105(立方厘米)
9.88cm2;48cm3
【分析】由图可知:长方体两条长+两条高的长度是16cm,高为2cm,所以长方体的长为(16-2×2)÷2=6cm;求表面将数据代入长方体表面积公式:S=(ab+ah+bh)×2计算即可,求体积将数据代入长方体体积公式:V=abh计算即可。
【详解】
=(16-4)÷2
=12÷2
=6(cm)
表面积:
=(12+8+24)×2
=44×2
=88(cm2)
体积:
=24×2
=48(cm3)
这个长方体的表面积是88cm2,体积是48cm3。
10.表面积是426cm2,体积是540cm3
【分析】观察展开图可知,长为12cm,宽为5cm,高为[(42-12×2)÷2]cm,也就是9cm,根据长方体的表面积=(长×宽+长×高+宽×高)×2,用(12×5+12×9+9×5)×2即可求出长方体的表面积,根据长方体的体积=长×宽×高,用12×5×9即可求出长方体体积。
【详解】(42-12×2)÷2
=(42-24)÷2
=18÷2
=9(cm)
表面积:(12×5+12×9+9×5)×2
=(60+108+45)×2
=213×2
=426(cm2)
体积:12×5×9
=60×9
=540(cm3)
这个长方体的表面积是426cm2,体积是540cm3。
11.760立方厘米
【分析】长方体的体积=长×宽×高,立体图形的体积=上面小长方体的体积+下面大长方体的体积,据此解答。
【详解】4×10×4+12×10×5
=40×4+120×5
=160+600
=760(立方厘米)
所以,立体图形的体积是760立方厘米。
12.表面积:184cm2,体积:147cm3
【分析】观察图形可知,该组合图形的表面积=长方体的表面积+正方体的表面积-两个正方形的面积;该组合图形的体积=长方体的体积+正方体的体积;然后根据长方体的表面积公式:S=(ab+ah+bh)×2,正方体的表面积公式:S=6a2,长方体的体积公式:V=abh,正方体的体积公式:V=a3,据此计算即可。
【详解】表面积:(6×4+6×5+4×5)×2+3×3×6-3×3×2
=(24+30+20)×2+54-18
=74×2+54-18
=148+54-18
=202-18
=184(cm2)
体积:6×4×5+3×3×3
=24×5+9×3
=120+27
=147(cm3)
13.表面积1204 cm2;体积2328cm3
【分析】组合图形的左边是正方体,右边是长方体,正方体和长方体有重合部分;把长方体的右面向左平移到重合部分,补给正方体的右面,这样正方体的表面积是6个面的面积之和,长方体的表面积只有上下面、前后面共4个面的面积;
组合图形的表面积=正方体的表面积+长方体4个面的面积,根据正方体的表面积=棱长×棱长×6,长方体4个面的面积=长×宽×2+长×高×2,代入数据计算即可;
组合图形的体积=正方体的体积+长方体的体积,根据正方体的体积=棱长×棱长×棱长,长方体的体积=长×宽×高,代入数据计算即可。
【详解】表面积:
12×12×6
=144×6
=864(cm2)
10×12×2+10×5×2
=240+100
=340(cm2)
864+340=1204(cm2)
体积:
12×12×12
=144×12
=1728(cm3)
10×12×5
=120×5
=600(cm3)
1728+600=2328(cm3)
14.232m2
【分析】由图可知,该几何体是由一个大长方体的表面积减去两个长(6-2)m和宽(4-2)m的长方形的面积,根据长方体的表面积公式,代入数据进行解答即可。
【详解】(10×6+10×4+4×6)×2
=(60+40+24)×2
=124×2
=248(m2)
2×(6-2)×(4-2)
=2×4×2
=8×2
=16(m2)
248-16=232(m2)
15.150cm3
【分析】结合图示可知:长方体容器长、宽都是10cm,原来水面高8.5cm,浸没一条鱼后水面上升至10cm;则鱼的体积就相当于上升部分水的体积,因为上升部分是长方体,所以可以套用长方体体积公式来计算,列式为:10×10×(10-8.5)。
【详解】10×10×(10-8.5)
=100×1.5
=150(cm3)
【点睛】本题运用了转化思想,把不规则物体的体积转化为规则物体的体积,其中注意关注水面上升的高度。
16.表面积:176cm2;体积:108cm3
【分析】本题考查立体图形堆叠在一起后体积和表面积的变化。该图形的体积=正方体的体积+长方体的体积;该图形的表面积=长方体表面积+正方体表面积-减少的两个正方形的面积。根据长方体的体积公式:V=abh,正方体的体积公式:V=a3,长方体的表面积公式:S=(ab+ah+bh)×2,正方体的表面积公式:S=6a2,据此代入数值进行计算即可。
【详解】表面积:
(10×2+10×5+2×5)×2
=(20+50+10)×2
=80×2
=160(cm2)
2×2×6=24(cm2)
2×2×2=8(cm2)
160+24-8
=184-8
=176(cm2)
体积:10×2×5+2×2×2
=20×5+8
=100+8
=108(cm3)
17.5.5平方厘米;0.75立方厘米
【分析】观察这个长方体的展开图,这个长方体的长是2-0.5=1.5(厘米),宽是1厘米,高是0.5厘米,再根据长方体的体积=长×宽×高,长方体的表面积=(长×宽+长×高+宽×高)×2代入数据进行计算即可。
【详解】这个长方体的长:2-0.5=1.5(厘米)
表面积:
(1.5×1+1.5×0.5+1×0.5)×2
=(1.5+0.75+0.5)×2
=2.75×2
=5.5(平方厘米)
体积:1.5×1×0.5=0.75(立方厘米)
18.234cm2;189cm3
【分析】从图中可以看出,几何体缺少1个棱长为3cm的小正方体,这个位置原来有2个面;挖去这个小正方体后,露出来4个面;所以几何体的表面积比原来大正方体的表面积多(4-2)个(3×3)的小正方形的面积;几何体的表面积=大正方体的表面积+2个小正方形的面积;几何体的体积=大正方体的体积-小正方体的体积;根据正方体的表面积=棱长×棱长×6,正方体的体积=棱长×棱长×棱长,代入数据计算即可。
【详解】6×6×6+3×3×(4-2)
=36×6+9×2
=216+18
=234(cm2)
6×6×6-3×3×3
=36×6-9×3
=216-27
=189(cm3)
19.100立方分米
【分析】根据长方体的体积公式:V=Sh,把数据代入公式解答即可。
【详解】1米=10分米
10×10=100(立方分米)
20.333dm3
【分析】这个图形的体积=长是12dm,宽是3dm,高是10dm的长方体体积-棱长是3dm的正方体体积;根据长方体体积公式:长×宽×高;正方体体积公式:棱长×棱长×棱长,代入数据,即可解答。
【详解】12×3×10-3×3×3
=36×10-9×3
=360-27
=333(dm3)
21.336立方厘米
【分析】如图,把这个长方体的长看作12厘米,宽看作7厘米,高×2+宽=15厘米,代入宽的长度,可求得高为4厘米,利用长方体的体积公式:V=abh,代入数据即可得解。
【详解】(15-7)÷2
=8÷2
=4(厘米)
12×7×4=336(立方厘米)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末图形计算专项:长方体和正方体-数学六年级上册苏教版
1.计算下面的体积。
2.计算图形的表面积和体积。(单位:分米)
3.下图中长方体长8厘米、宽6厘米、高4厘米,正方体的棱长是5厘米。请计算组合体的表面积和体积。
4.计算下面图形的表面积和体积。(单位:m)
5.计算下面几何体的表面积和体积。
6.求下面图形的表面积和体积。(单位:厘米)
7.求出下面图形的体积。(单位:cm)
8.分别求下左图中正方体的表面积和体积和下右图中围成的长方体的表面积和体积。(单位:cm)
9.下图是一个长方体的表面展开图,求出这个长方体的表面积和体积。
10.如图,这是一个长方体模型的展开图,求它的表面积和体积。
11.计算下面立体图形的体积。(单位:厘米)
12.求下列图形的表面积和体积。
13.计算下面组合图形的表面积和体积。
14.求出下列图形的表面积。
15.观察下图,计算鱼的体积。
16.计算下面图形的体积和表面积。
17.下图是一个长方体展开图中的三个面,请根据图中数据计算出这个长方体的表面积和体积。
18.计算下面图形的表面积和体积。
19.求长方体的体积。
20.计算下面图形的体积。
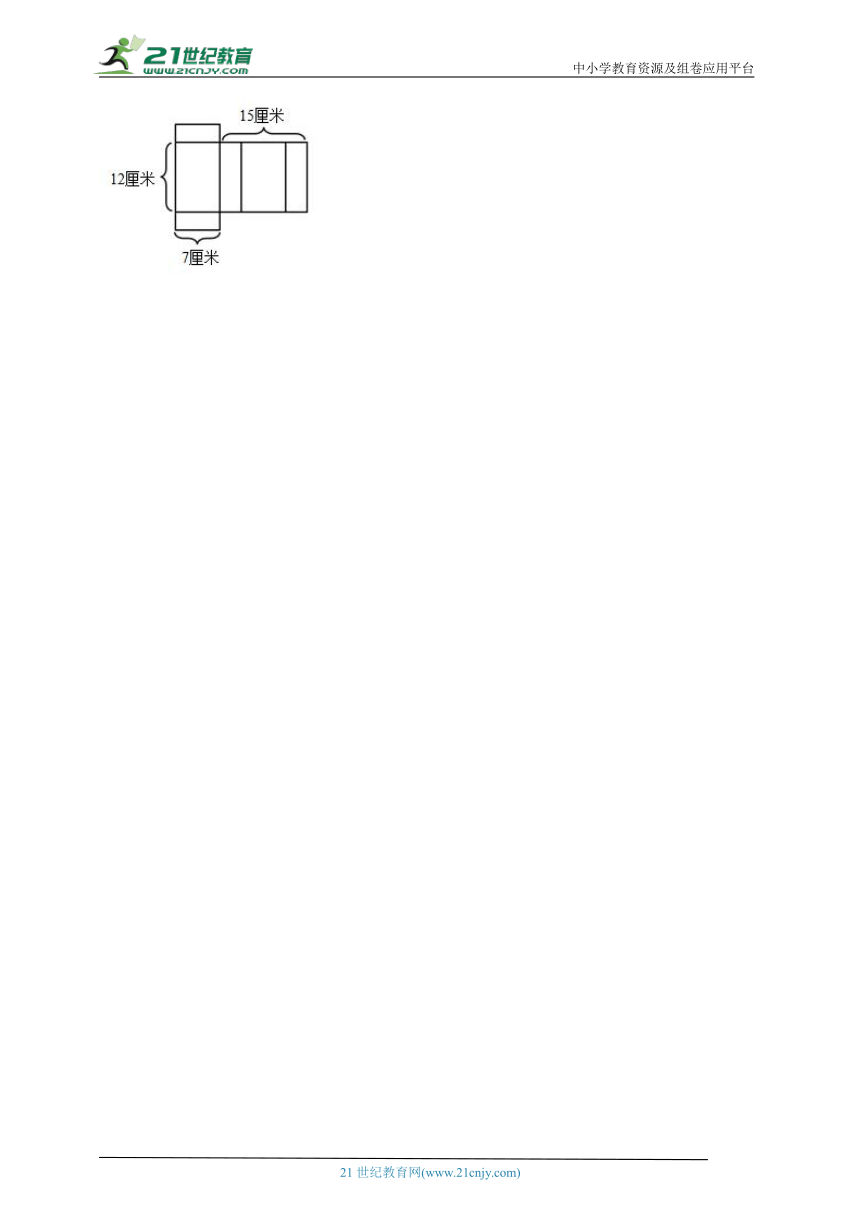
21.下面是一个长方体的展开图,请根据图中的数据求出长方体的体积。
参考答案:
1.84cm3;216dm3
【分析】根据长方体体积公式,用7×3×4即可求出长方体的体积;
根据正方体的体积公式,用6×6×6即可求出正方体的体积。
【详解】7×3×4
=21×4
=84(cm3)
长方体的体积是84cm3。
6×6×6
=36×6
=216(dm3)
正方体的体积是216dm3。
2.184平方分米;160立方分米;37.5平方分米;15.625立方分米
【分析】根据长方体的表面积公式,用(8×4+8×5+4×5)×2即可求出长方体的表面积;
根据长方体的体积公式,用8×5×4即可求出长方体的体积;
根据正方体的表面积公式,用2.5×2.5×6即可求出正方体的表面积;
根据正方体的体积公式,用2.5×2.5×2.5即可求出正方体的体积。
【详解】(8×4+8×5+4×5)×2
=(32+40+20)×2
=92×2
=184(平方分米)
长方体的表面积是184平方分米。
8×5×4
=40×4
=160(立方分米)
长方体的体积是160立方分米。
2.5×2.5×6
=6.25×6
=37.5(平方分米)
正方体的表面积是37.5平方分米。
2.5×2.5×2.5
=6.25×2.5
=15.625(立方分米)
正方体的体积是15.625立方分米。
3.308平方厘米;317立方厘米
【分析】组合体的表面积=完整的长方体表面积+正方体4个面的面积和,长方体表面积=(长×宽+长×高+宽×高)×2;组合体的体积=长方体体积+正方体体积,长方体体积=长×宽×高,正方体体积=棱长×棱长×棱长,据此列式计算。
【详解】(8×6+8×4+6×4)×2+5×5×4
=(48+32+24)×2+100
=104×2+100
=208+100
=308(平方厘米)
8×6×4+5×5×5
=192+125
=317(立方厘米)
4.表面积428m2;体积453m3
【分析】观察图形可知,在长方体上面挖出一个正方体,长方体的表面积增加了正方体的4个侧面面积。长方体的表面积=(长×宽+长×高+宽×高)×2,正方体4个侧面面积=棱长×棱长×4,据此代入数据计算,再把它们加起来即可。
用长方体的体积减去正方体的体积即是这个图形的体积。长方体的体积=长×宽×高,正方体的体积=棱长×棱长×棱长,据此解答。
【详解】表面积:(12×8+12×5+8×5)×2+3×3×4
=(96+60+40)×2+36
=196×2+36
=392+36
=428(m2)
体积:12×8×5-3×3×3
=480-27
=453(m3)
5.1220m2;2445m3
【分析】长方体的表面积=(长×宽+宽×高+长×高)×2,长方体的体积=长×宽×高,几何体的表面积=大长方体的表面积+小长方体4个侧面的面积,几何体的体积=大长方体的体积+小长方体的体积,据此解答。
【详解】表面积:(20×8+20×15+8×15)×2+5×3×4
=(160+300+120)×2+5×3×4
=580×2+5×3×4
=1160+60
=1220(m2)
体积:20×8×15+5×3×3
=160×15+15×3
=2400+45
=2445(m3)
所以,这个几何体的表面积是1220m2,体积是2445m3。
6.216平方厘米;204立方厘米
【分析】组合体的表面积=大正方体表面积,正方体表面积=棱长×棱长×6;组合体体积=大正方体体积-小长方体体积,正方体体积=棱长×棱长×棱长,长方体体积=棱长×棱长×棱长,据此列式计算。
【详解】(平方厘米)
(立方厘米)
7.31cm3
【分析】组合图形的体积=正方体的体积+长方体的体积;根据正方体的体积=棱长×棱长×棱长,长方体的体积=长×宽×高,代入数据计算即可。
【详解】3×3×3+4×1×1
=27+4
=31(cm3)
图形的体积是31cm3。
8.左图正方体:表面积是96平方厘米;体积是64立方厘米
右图长方体:表面积是142平方厘米;体积是105立方厘米
【分析】正方体的表面积=棱长×棱长×6,正方体的体积=棱长×棱长×棱长,由此代入数据即可解答;长方体的表面积=(长×宽+长×高+宽×高)×2,长方体的体积=长×宽×高
【详解】正方体的表面积是:
4×4×6
=16×6
=96(平方厘米)
体积是:
4×4×4
=16×4
=64(立方厘米)
长方体的表面积是:
(7×5+5×3+7×3)×2
=(35+15+21)×2
=71×2
=142(平方厘米)
体积是:
7×5×3
=35×3
=105(立方厘米)
9.88cm2;48cm3
【分析】由图可知:长方体两条长+两条高的长度是16cm,高为2cm,所以长方体的长为(16-2×2)÷2=6cm;求表面将数据代入长方体表面积公式:S=(ab+ah+bh)×2计算即可,求体积将数据代入长方体体积公式:V=abh计算即可。
【详解】
=(16-4)÷2
=12÷2
=6(cm)
表面积:
=(12+8+24)×2
=44×2
=88(cm2)
体积:
=24×2
=48(cm3)
这个长方体的表面积是88cm2,体积是48cm3。
10.表面积是426cm2,体积是540cm3
【分析】观察展开图可知,长为12cm,宽为5cm,高为[(42-12×2)÷2]cm,也就是9cm,根据长方体的表面积=(长×宽+长×高+宽×高)×2,用(12×5+12×9+9×5)×2即可求出长方体的表面积,根据长方体的体积=长×宽×高,用12×5×9即可求出长方体体积。
【详解】(42-12×2)÷2
=(42-24)÷2
=18÷2
=9(cm)
表面积:(12×5+12×9+9×5)×2
=(60+108+45)×2
=213×2
=426(cm2)
体积:12×5×9
=60×9
=540(cm3)
这个长方体的表面积是426cm2,体积是540cm3。
11.760立方厘米
【分析】长方体的体积=长×宽×高,立体图形的体积=上面小长方体的体积+下面大长方体的体积,据此解答。
【详解】4×10×4+12×10×5
=40×4+120×5
=160+600
=760(立方厘米)
所以,立体图形的体积是760立方厘米。
12.表面积:184cm2,体积:147cm3
【分析】观察图形可知,该组合图形的表面积=长方体的表面积+正方体的表面积-两个正方形的面积;该组合图形的体积=长方体的体积+正方体的体积;然后根据长方体的表面积公式:S=(ab+ah+bh)×2,正方体的表面积公式:S=6a2,长方体的体积公式:V=abh,正方体的体积公式:V=a3,据此计算即可。
【详解】表面积:(6×4+6×5+4×5)×2+3×3×6-3×3×2
=(24+30+20)×2+54-18
=74×2+54-18
=148+54-18
=202-18
=184(cm2)
体积:6×4×5+3×3×3
=24×5+9×3
=120+27
=147(cm3)
13.表面积1204 cm2;体积2328cm3
【分析】组合图形的左边是正方体,右边是长方体,正方体和长方体有重合部分;把长方体的右面向左平移到重合部分,补给正方体的右面,这样正方体的表面积是6个面的面积之和,长方体的表面积只有上下面、前后面共4个面的面积;
组合图形的表面积=正方体的表面积+长方体4个面的面积,根据正方体的表面积=棱长×棱长×6,长方体4个面的面积=长×宽×2+长×高×2,代入数据计算即可;
组合图形的体积=正方体的体积+长方体的体积,根据正方体的体积=棱长×棱长×棱长,长方体的体积=长×宽×高,代入数据计算即可。
【详解】表面积:
12×12×6
=144×6
=864(cm2)
10×12×2+10×5×2
=240+100
=340(cm2)
864+340=1204(cm2)
体积:
12×12×12
=144×12
=1728(cm3)
10×12×5
=120×5
=600(cm3)
1728+600=2328(cm3)
14.232m2
【分析】由图可知,该几何体是由一个大长方体的表面积减去两个长(6-2)m和宽(4-2)m的长方形的面积,根据长方体的表面积公式,代入数据进行解答即可。
【详解】(10×6+10×4+4×6)×2
=(60+40+24)×2
=124×2
=248(m2)
2×(6-2)×(4-2)
=2×4×2
=8×2
=16(m2)
248-16=232(m2)
15.150cm3
【分析】结合图示可知:长方体容器长、宽都是10cm,原来水面高8.5cm,浸没一条鱼后水面上升至10cm;则鱼的体积就相当于上升部分水的体积,因为上升部分是长方体,所以可以套用长方体体积公式来计算,列式为:10×10×(10-8.5)。
【详解】10×10×(10-8.5)
=100×1.5
=150(cm3)
【点睛】本题运用了转化思想,把不规则物体的体积转化为规则物体的体积,其中注意关注水面上升的高度。
16.表面积:176cm2;体积:108cm3
【分析】本题考查立体图形堆叠在一起后体积和表面积的变化。该图形的体积=正方体的体积+长方体的体积;该图形的表面积=长方体表面积+正方体表面积-减少的两个正方形的面积。根据长方体的体积公式:V=abh,正方体的体积公式:V=a3,长方体的表面积公式:S=(ab+ah+bh)×2,正方体的表面积公式:S=6a2,据此代入数值进行计算即可。
【详解】表面积:
(10×2+10×5+2×5)×2
=(20+50+10)×2
=80×2
=160(cm2)
2×2×6=24(cm2)
2×2×2=8(cm2)
160+24-8
=184-8
=176(cm2)
体积:10×2×5+2×2×2
=20×5+8
=100+8
=108(cm3)
17.5.5平方厘米;0.75立方厘米
【分析】观察这个长方体的展开图,这个长方体的长是2-0.5=1.5(厘米),宽是1厘米,高是0.5厘米,再根据长方体的体积=长×宽×高,长方体的表面积=(长×宽+长×高+宽×高)×2代入数据进行计算即可。
【详解】这个长方体的长:2-0.5=1.5(厘米)
表面积:
(1.5×1+1.5×0.5+1×0.5)×2
=(1.5+0.75+0.5)×2
=2.75×2
=5.5(平方厘米)
体积:1.5×1×0.5=0.75(立方厘米)
18.234cm2;189cm3
【分析】从图中可以看出,几何体缺少1个棱长为3cm的小正方体,这个位置原来有2个面;挖去这个小正方体后,露出来4个面;所以几何体的表面积比原来大正方体的表面积多(4-2)个(3×3)的小正方形的面积;几何体的表面积=大正方体的表面积+2个小正方形的面积;几何体的体积=大正方体的体积-小正方体的体积;根据正方体的表面积=棱长×棱长×6,正方体的体积=棱长×棱长×棱长,代入数据计算即可。
【详解】6×6×6+3×3×(4-2)
=36×6+9×2
=216+18
=234(cm2)
6×6×6-3×3×3
=36×6-9×3
=216-27
=189(cm3)
19.100立方分米
【分析】根据长方体的体积公式:V=Sh,把数据代入公式解答即可。
【详解】1米=10分米
10×10=100(立方分米)
20.333dm3
【分析】这个图形的体积=长是12dm,宽是3dm,高是10dm的长方体体积-棱长是3dm的正方体体积;根据长方体体积公式:长×宽×高;正方体体积公式:棱长×棱长×棱长,代入数据,即可解答。
【详解】12×3×10-3×3×3
=36×10-9×3
=360-27
=333(dm3)
21.336立方厘米
【分析】如图,把这个长方体的长看作12厘米,宽看作7厘米,高×2+宽=15厘米,代入宽的长度,可求得高为4厘米,利用长方体的体积公式:V=abh,代入数据即可得解。
【详解】(15-7)÷2
=8÷2
=4(厘米)
12×7×4=336(立方厘米)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
