人教版数学九年级上册第二十二章 二次函数 单元测评卷(含解析)
文档属性
| 名称 | 人教版数学九年级上册第二十二章 二次函数 单元测评卷(含解析) | 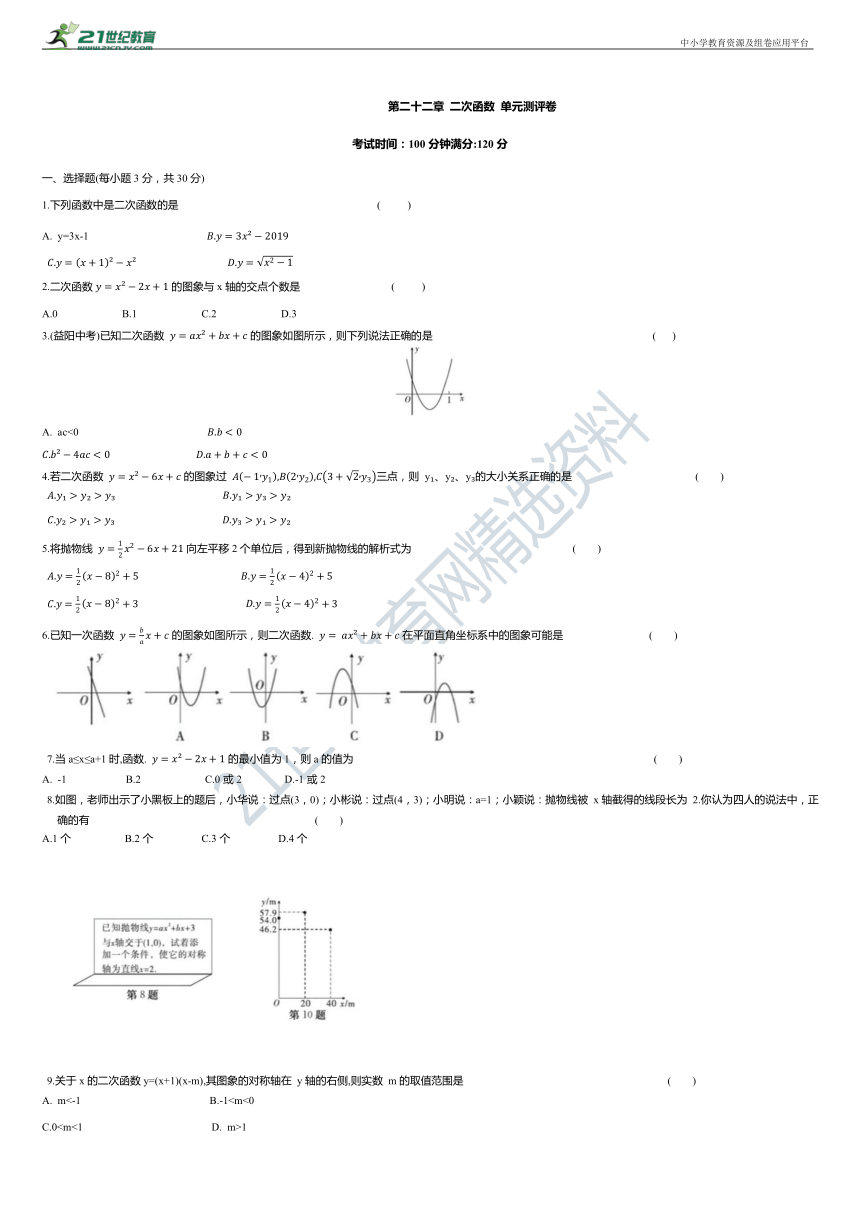 | |
| 格式 | docx | ||
| 文件大小 | 464.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-17 21:50:54 | ||
图片预览


文档简介
第二十二章 二次函数 单元测评卷
考试时间:100分钟满分:120分
一、选择题(每小题3分,共30分)
1.下列函数中是二次函数的是 ( )
A. y=3x-1
2.二次函数的图象与x轴的交点个数是 ( )
A.0 B.1 C.2 D.3
3.(益阳中考)已知二次函数 的图象如图所示,则下列说法正确的是 ( )
A. ac<0
4.若二次函数 的图象过 三点,则 y 、y 、y 的大小关系正确的是 ( )
5.将抛物线 向左平移2个单位后,得到新抛物线的解析式为 ( )
6.已知一次函数 的图象如图所示,则二次函数. 在平面直角坐标系中的图象可能是 ( )
7.当a≤x≤a+1时,函数. 的最小值为1,则a的值为 ( )
A. -1 B.2 C.0或2 D.-1或2
8.如图,老师出示了小黑板上的题后,小华说:过点(3,0);小彬说:过点(4,3);小明说:a=1;小颖说:抛物线被 x轴截得的线段长为 2.你认为四人的说法中,正确的有 ( )
A.1个 B.2个 C.3个 D.4个
9.关于x的二次函数y=(x+1)(x-m),其图象的对称轴在 y轴的右侧,则实数 m的取值范围是 ( )
A. m<-1 B.-1C.01
10.跳台滑雪是冬季奥运会比赛项目之一.运动员起跳后的飞行路线可以看作是抛物线的一部分,运动员起跳后的竖直高度y(单位:m)与水平距离x(单位:m)近似满足函数关系 如图记录了某运动员起跳后的x与y的三组数据,根据上述函数模型和数据,可推断出该运动员起跳后飞行到最高点时,水平距离为( )
A.10m B.15m C.20m D.22.5m
二、填空题(每小题3分,共 15 分)
11.抛物线 的顶点坐标为 .
12.如果函数 是二次函数,那么k的值一定是 .
13.某一型号飞机着陆后滑行的距离y(米)与滑行时间x(秒)之间的函数解析式是 该型号飞机着陆后需滑行 米才能停下来.
14.已知函数 与函数 的图象大致如图所示.若 ,则自变量x的取值范围是 .
15.如图所示,一座大桥有一段抛物线形的拱梁,抛物线的表达式为 小强骑自行车从拱梁一端O沿直线匀速穿过拱梁部分的桥面OC,当小强骑自行车行驶 10s时和26s时拱梁的高度相同,则小强骑自行车通过拱梁部分的桥面OC共需 s.
三、解答题(本大题共8小题,满分75 分)
16.(8分)已知抛物线
(1)求它的对称轴;
(2)求它与x轴、y轴的交点坐标.
17.(9分)如图,(1)写出二次函数的解析式;
(2)观察图象写出 时,x的取值范围.
中小学教育资源及组卷应用平台
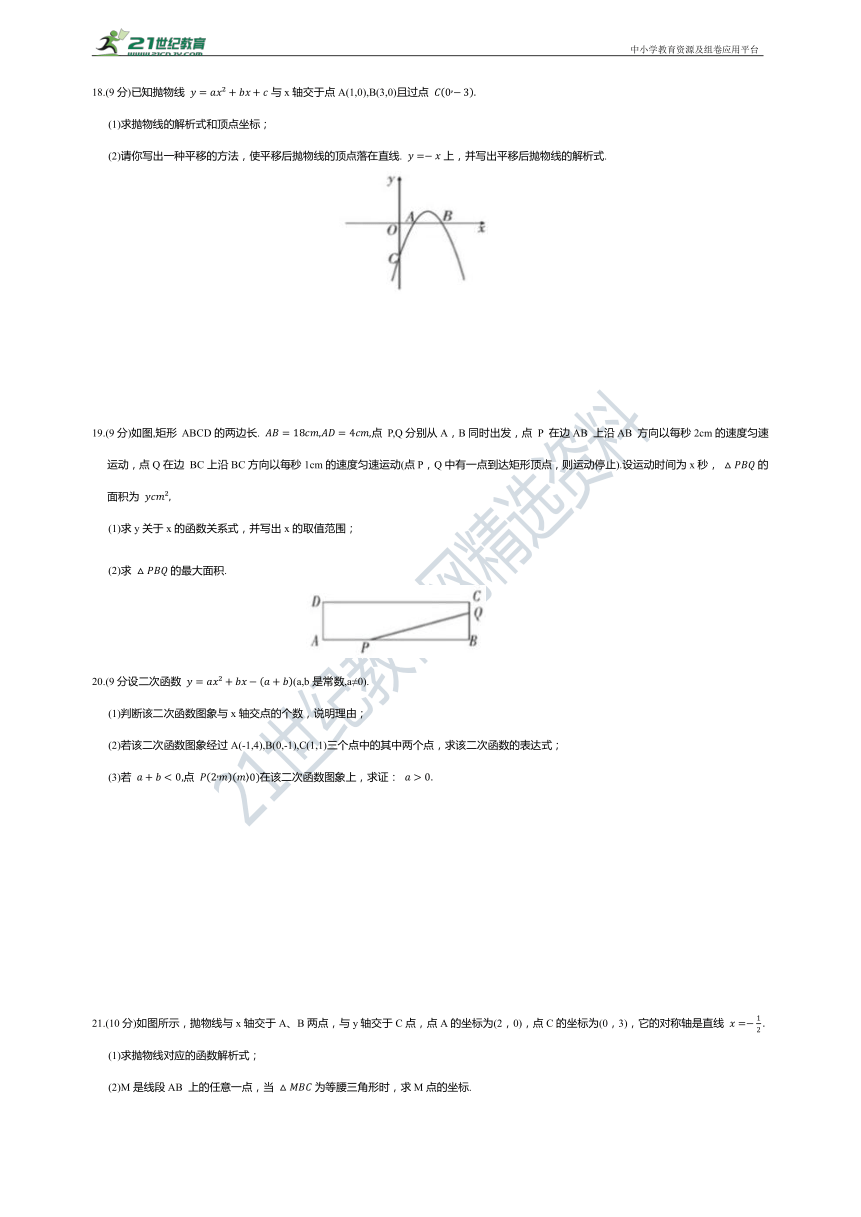
18.(9分)已知抛物线 与x轴交于点A(1,0),B(3,0)且过点
(1)求抛物线的解析式和顶点坐标;
(2)请你写出一种平移的方法,使平移后抛物线的顶点落在直线. 上,并写出平移后抛物线的解析式.
19.(9分)如图,矩形 ABCD的两边长. 点 P,Q分别从A,B同时出发,点 P 在边AB 上沿AB 方向以每秒2cm的速度匀速运动,点Q在边 BC上沿BC方向以每秒1cm的速度匀速运动(点P,Q中有一点到达矩形顶点,则运动停止).设运动时间为x秒, 的面积为
(1)求y关于x的函数关系式,并写出x的取值范围;
(2)求 的最大面积.
20.(9分设二次函数 (a,b是常数,a≠0).
(1)判断该二次函数图象与x轴交点的个数,说明理由;
(2)若该二次函数图象经过A(-1,4),B(0,-1),C(1,1)三个点中的其中两个点,求该二次函数的表达式;
(3)若 点 在该二次函数图象上,求证:
21.(10分)如图所示,抛物线与x轴交于A、B两点,与y轴交于C点,点A的坐标为(2,0),点C的坐标为(0,3),它的对称轴是直线
(1)求抛物线对应的函数解析式;
(2)M是线段AB 上的任意一点,当 为等腰三角形时,求M点的坐标.
22.(10分)如图,已知抛物线 与一直线相交于 C(2.3)两点,与y轴交于点N,其顶点为 D.
(1)求抛物线及直线AC的函数解析式;
(2)设点 M(3,m),求使. 的值最小时m 的值.
23.(11分))“绿水青山就是金山银山”的理念已融入人们的日常生活中,因此,越来越多的人喜欢骑自行车出行.某自行车店在销售某型号自行车时,以高出进价的50%标价.已知按标价九折销售该型号自行车8辆与将标价直降100元销售7辆获利相同.
(1)求该型号自行车的进价和标价分别是多少元.
(2)若该型号自行车的进价不变,按(1)中的标价出售,该店平均每月可售出51辆;若每辆自行车每降价 20元,每月可多售出3辆,求该型号自行车每辆降价多少元时,每月获利最大,最大利润是多少
一、1. B 2. B
3. B 解析:A.∵抛物线开口向上,∴a>0,∵抛物线与y轴交于正半轴,∴c>0,∴ac>0,故A 选项错误;B.∵对称轴在y轴右侧,∴a、b异号,∴b<0,故B选项正确;C.∵抛物线与x轴有两个交点, 故C选项错误;D.由题图可知,当x=1时,y=a+b+c>0,故 D选项错误.所以选B.
4. B
5. D 解析:将抛物线解析式化为顶点式,即 根据函数图象平移规律“左加右减”,则将此抛物线向左平移2个单位后,得到新抛物线的解析式为
6. A 解析:由题图中一次函数 的图象可知 对于二次函数 ∴它的图象与y轴的交点在x轴上方,且对称轴在y轴右侧,故只有选项A中的图象符合题意.
7. D 解析:当 y=1时,有 解得 当a≤x≤a+1时,函数有最小值1.∴a+1=0或a=2,解得a=-1或2,故选D.
8. C
9. D 解析:二次函数化为一般形式,得 所以对称轴方程为 因为对称轴在y轴的右侧,所以m-1>0,解得m>1.故选D.
10. B 解析:由题意可知c=54,把(20,57.9)和(40,46.2)分别代入
得 解得
故该抛物线的解析式为 对称轴为直线 即该运动员起跳后飞行到最高点时,水平距离为15m.
二、11.(1.3)
12.0 解析:根据二次函数的定义,得k -3k+2=2,解得k=0或k=3.又∵k-3≠0,∴k≠3.∴当k=0时,这个函数是二次函数.
13.600 14.-215.36 解析:如图所示,设在10s时小强到达A处,在26s时小强到达B处,线段OC的中点是D.∵行驶10s时和26s时拱梁的高度相同,∴A,B两点关于对称轴对称.∵从A 处到B 处需要16s,从A处到D处需要8s.∴从O处到D 处需要10+8=18(s).∴从O处到C处需要2×18=36(s).
三、16.解:(1)对称轴为 (2)把y=0代入y= 得 解这个方程,得.x =3,x =- 所以抛物线与x轴的交点坐标为(3.0)(- .0).把 x=0代入 得y=-3,所以抛物线与y轴交于点(0,-3).
17.解:(1)由图象知抛物线的对称轴是x=-1,顶点坐标是(-1,2),过原点(0,0)和点(-2,0).设二次函数的解析为 过原点(0,0),∴a+2=0,a=-2,故二次函数的解析式为 y 即 (2)由图象可知:当y>0时,x的取值范围是-218.解:(1)∵抛物线与x轴交于点A(1,0),B(3,0),∴可设抛物线的解析式为 y=a(x-1)(x-3),把C(0,-3)代入得3a=-3,解得a=-1,故抛物线的解析式为 y=-(x-1)(x-3),即 .顶点坐标为(2.1). (2)先向左平移2个单位,再向下平移1个单位,得到的抛物线的解析式为 y=-x ,平移后抛物线的顶点(0,0)落在直线 y=-x上.
19.解:(1)∵S△mq= PB·BQ,PB=AB-AP=18-2x,BQ=x,∴y= (18-2x)x,l即 +9x(020.(1)解:∵a≠0,∴b -4ac=b +4a(a+b)=(b+2a) ≥0,∴二次函数与x轴有1个或2个交点:(2)解:由(1)可知,函数过(1,0),∴图象不经过(1,1),即只经过A、B两点,将A(-1,4),B(0,-1)代入 中得 解得 (3)证明:∵P(2,m)在二次函数图象上,∴m=4a+2b-(a+b)=3a+b=a+b+2a,又∵a+b<0,m>0,∴2a>0,即a>0.
21.解:(1)设抛物线对应的函数解析式为 把 A(2,0),C(0,3)代入得 解得 耳 (2)由y=0得 时,∵BO=CO=3,即△BOC是等腰直角三角形,∴M点的坐标为(0,0).②BC=BM时,在 Rt△BOC中,BO=CO=3,由勾股定理得 M点的坐标为( 即点M 的坐标为(0,0)或
22.解:(1)由抛物线. 过点A(-1,0)及C(2,3),得 解得 故抛物线为 又设直线AC为y=kx+n,由A(-1,0)及C(2,3)得 解得 故直线AC为y=x+1. (2)由(1)易得点 N(0,3),作点 N关于直线x=3的对称点 N′,则 N'(6.3).由(1)得 D(1.4),故直线 DN'的函数解析式为 当M(3,m)在直线DN'上时,MN+MD的值最小,则
23.解:(1)设该型号自行车的进价为x元/辆,则标价为(1+50%)x元/辆.根据题意,得8[(1+50%)x×0.9-x]=7[(1+50%)x-100-x],整理得2.8x=3.5x-700,解得x=1000,(1+50%)x=(1+50%)×1000=1500(元/辆).答:该型号自行车的进价为 1000元/辆,标价为 1500 元/辆.(2)设该型号自行车每辆降价a元,每月获利 W 元.根据题意,得 W=(1500-1000-a) ∴当a=80时,W 最大,为26460.答:该型号自行车每辆降价80元时,每月获利最大,最大利润是 26460元.
考试时间:100分钟满分:120分
一、选择题(每小题3分,共30分)
1.下列函数中是二次函数的是 ( )
A. y=3x-1
2.二次函数的图象与x轴的交点个数是 ( )
A.0 B.1 C.2 D.3
3.(益阳中考)已知二次函数 的图象如图所示,则下列说法正确的是 ( )
A. ac<0
4.若二次函数 的图象过 三点,则 y 、y 、y 的大小关系正确的是 ( )
5.将抛物线 向左平移2个单位后,得到新抛物线的解析式为 ( )
6.已知一次函数 的图象如图所示,则二次函数. 在平面直角坐标系中的图象可能是 ( )
7.当a≤x≤a+1时,函数. 的最小值为1,则a的值为 ( )
A. -1 B.2 C.0或2 D.-1或2
8.如图,老师出示了小黑板上的题后,小华说:过点(3,0);小彬说:过点(4,3);小明说:a=1;小颖说:抛物线被 x轴截得的线段长为 2.你认为四人的说法中,正确的有 ( )
A.1个 B.2个 C.3个 D.4个
9.关于x的二次函数y=(x+1)(x-m),其图象的对称轴在 y轴的右侧,则实数 m的取值范围是 ( )
A. m<-1 B.-1
10.跳台滑雪是冬季奥运会比赛项目之一.运动员起跳后的飞行路线可以看作是抛物线的一部分,运动员起跳后的竖直高度y(单位:m)与水平距离x(单位:m)近似满足函数关系 如图记录了某运动员起跳后的x与y的三组数据,根据上述函数模型和数据,可推断出该运动员起跳后飞行到最高点时,水平距离为( )
A.10m B.15m C.20m D.22.5m
二、填空题(每小题3分,共 15 分)
11.抛物线 的顶点坐标为 .
12.如果函数 是二次函数,那么k的值一定是 .
13.某一型号飞机着陆后滑行的距离y(米)与滑行时间x(秒)之间的函数解析式是 该型号飞机着陆后需滑行 米才能停下来.
14.已知函数 与函数 的图象大致如图所示.若 ,则自变量x的取值范围是 .
15.如图所示,一座大桥有一段抛物线形的拱梁,抛物线的表达式为 小强骑自行车从拱梁一端O沿直线匀速穿过拱梁部分的桥面OC,当小强骑自行车行驶 10s时和26s时拱梁的高度相同,则小强骑自行车通过拱梁部分的桥面OC共需 s.
三、解答题(本大题共8小题,满分75 分)
16.(8分)已知抛物线
(1)求它的对称轴;
(2)求它与x轴、y轴的交点坐标.
17.(9分)如图,(1)写出二次函数的解析式;
(2)观察图象写出 时,x的取值范围.
中小学教育资源及组卷应用平台
18.(9分)已知抛物线 与x轴交于点A(1,0),B(3,0)且过点
(1)求抛物线的解析式和顶点坐标;
(2)请你写出一种平移的方法,使平移后抛物线的顶点落在直线. 上,并写出平移后抛物线的解析式.
19.(9分)如图,矩形 ABCD的两边长. 点 P,Q分别从A,B同时出发,点 P 在边AB 上沿AB 方向以每秒2cm的速度匀速运动,点Q在边 BC上沿BC方向以每秒1cm的速度匀速运动(点P,Q中有一点到达矩形顶点,则运动停止).设运动时间为x秒, 的面积为
(1)求y关于x的函数关系式,并写出x的取值范围;
(2)求 的最大面积.
20.(9分设二次函数 (a,b是常数,a≠0).
(1)判断该二次函数图象与x轴交点的个数,说明理由;
(2)若该二次函数图象经过A(-1,4),B(0,-1),C(1,1)三个点中的其中两个点,求该二次函数的表达式;
(3)若 点 在该二次函数图象上,求证:
21.(10分)如图所示,抛物线与x轴交于A、B两点,与y轴交于C点,点A的坐标为(2,0),点C的坐标为(0,3),它的对称轴是直线
(1)求抛物线对应的函数解析式;
(2)M是线段AB 上的任意一点,当 为等腰三角形时,求M点的坐标.
22.(10分)如图,已知抛物线 与一直线相交于 C(2.3)两点,与y轴交于点N,其顶点为 D.
(1)求抛物线及直线AC的函数解析式;
(2)设点 M(3,m),求使. 的值最小时m 的值.
23.(11分))“绿水青山就是金山银山”的理念已融入人们的日常生活中,因此,越来越多的人喜欢骑自行车出行.某自行车店在销售某型号自行车时,以高出进价的50%标价.已知按标价九折销售该型号自行车8辆与将标价直降100元销售7辆获利相同.
(1)求该型号自行车的进价和标价分别是多少元.
(2)若该型号自行车的进价不变,按(1)中的标价出售,该店平均每月可售出51辆;若每辆自行车每降价 20元,每月可多售出3辆,求该型号自行车每辆降价多少元时,每月获利最大,最大利润是多少
一、1. B 2. B
3. B 解析:A.∵抛物线开口向上,∴a>0,∵抛物线与y轴交于正半轴,∴c>0,∴ac>0,故A 选项错误;B.∵对称轴在y轴右侧,∴a、b异号,∴b<0,故B选项正确;C.∵抛物线与x轴有两个交点, 故C选项错误;D.由题图可知,当x=1时,y=a+b+c>0,故 D选项错误.所以选B.
4. B
5. D 解析:将抛物线解析式化为顶点式,即 根据函数图象平移规律“左加右减”,则将此抛物线向左平移2个单位后,得到新抛物线的解析式为
6. A 解析:由题图中一次函数 的图象可知 对于二次函数 ∴它的图象与y轴的交点在x轴上方,且对称轴在y轴右侧,故只有选项A中的图象符合题意.
7. D 解析:当 y=1时,有 解得 当a≤x≤a+1时,函数有最小值1.∴a+1=0或a=2,解得a=-1或2,故选D.
8. C
9. D 解析:二次函数化为一般形式,得 所以对称轴方程为 因为对称轴在y轴的右侧,所以m-1>0,解得m>1.故选D.
10. B 解析:由题意可知c=54,把(20,57.9)和(40,46.2)分别代入
得 解得
故该抛物线的解析式为 对称轴为直线 即该运动员起跳后飞行到最高点时,水平距离为15m.
二、11.(1.3)
12.0 解析:根据二次函数的定义,得k -3k+2=2,解得k=0或k=3.又∵k-3≠0,∴k≠3.∴当k=0时,这个函数是二次函数.
13.600 14.-2
三、16.解:(1)对称轴为 (2)把y=0代入y= 得 解这个方程,得.x =3,x =- 所以抛物线与x轴的交点坐标为(3.0)(- .0).把 x=0代入 得y=-3,所以抛物线与y轴交于点(0,-3).
17.解:(1)由图象知抛物线的对称轴是x=-1,顶点坐标是(-1,2),过原点(0,0)和点(-2,0).设二次函数的解析为 过原点(0,0),∴a+2=0,a=-2,故二次函数的解析式为 y 即 (2)由图象可知:当y>0时,x的取值范围是-2
19.解:(1)∵S△mq= PB·BQ,PB=AB-AP=18-2x,BQ=x,∴y= (18-2x)x,l即 +9x(0
21.解:(1)设抛物线对应的函数解析式为 把 A(2,0),C(0,3)代入得 解得 耳 (2)由y=0得 时,∵BO=CO=3,即△BOC是等腰直角三角形,∴M点的坐标为(0,0).②BC=BM时,在 Rt△BOC中,BO=CO=3,由勾股定理得 M点的坐标为( 即点M 的坐标为(0,0)或
22.解:(1)由抛物线. 过点A(-1,0)及C(2,3),得 解得 故抛物线为 又设直线AC为y=kx+n,由A(-1,0)及C(2,3)得 解得 故直线AC为y=x+1. (2)由(1)易得点 N(0,3),作点 N关于直线x=3的对称点 N′,则 N'(6.3).由(1)得 D(1.4),故直线 DN'的函数解析式为 当M(3,m)在直线DN'上时,MN+MD的值最小,则
23.解:(1)设该型号自行车的进价为x元/辆,则标价为(1+50%)x元/辆.根据题意,得8[(1+50%)x×0.9-x]=7[(1+50%)x-100-x],整理得2.8x=3.5x-700,解得x=1000,(1+50%)x=(1+50%)×1000=1500(元/辆).答:该型号自行车的进价为 1000元/辆,标价为 1500 元/辆.(2)设该型号自行车每辆降价a元,每月获利 W 元.根据题意,得 W=(1500-1000-a) ∴当a=80时,W 最大,为26460.答:该型号自行车每辆降价80元时,每月获利最大,最大利润是 26460元.
同课章节目录
