期末易错精选题检测卷-2023-2024学年数学九年级上册苏科版(含解析)
文档属性
| 名称 | 期末易错精选题检测卷-2023-2024学年数学九年级上册苏科版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-16 21:34:24 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
期末易错精选题检测卷-2023-2024学年数学九年级上册苏科版
一、单选题
1.在学校举办的合唱比赛中,八(3)班的演唱质量、精神风貌、配合默契得分分别为92分,80分,70分,若最终成绩由这三项得分依次按照 ,,的百分比确定,则八(3)班的最终成绩是 ( )
A.80.6分 B.81.8分 C.84.7分 D.96.8分
2.一元二次方程的根是( )
A.0 B.2 C.0,2 D.1,2
3.某校发起了“圆贫困地区孩子一个读书梦”的爱心捐书公益活动,在短短一周时间内,就收到了同学们捐赠的大量书籍. 现从中随机调查了部分学生的捐赠情况,并将收集到的数据统计如下:
数量/本 30 22 16 8 6 4
人数 40 30 25 50 20 35
根据表中的信息判断,下列结论正确的是( )
A.该校参与调查的学生有86人
B.该校参与调查的学生捐赠书籍的中位数为12本
C.该校参与调查的学生捐赠书籍的众数为8本
D.该校参与调查的学生平均捐赠书籍16本
4.汉代数学家赵爽在注解《周髀算经》时,给出的“赵爽弦图”是我国古代数学的瑰宝.如图,这个弦图中的四个直角三角形都是全等的,它们的两直角边的长分别是2和3.现随机向该图形内掷一枚飞镖,则飞镖落在阴影区域的概率为( )
A. B. C. D.
5.10月8日,杭州亚运会乒乓球比赛全部结束,国乒揽获除女双项目外的6块金牌,展现了在乒乓球领域强大的统治力.乒乓球比赛采用双循环制(每两队之间都进行两场比赛),比赛总场数为380场,若设参赛队伍有x支,则可列方程为( )
A. B.
C. D.
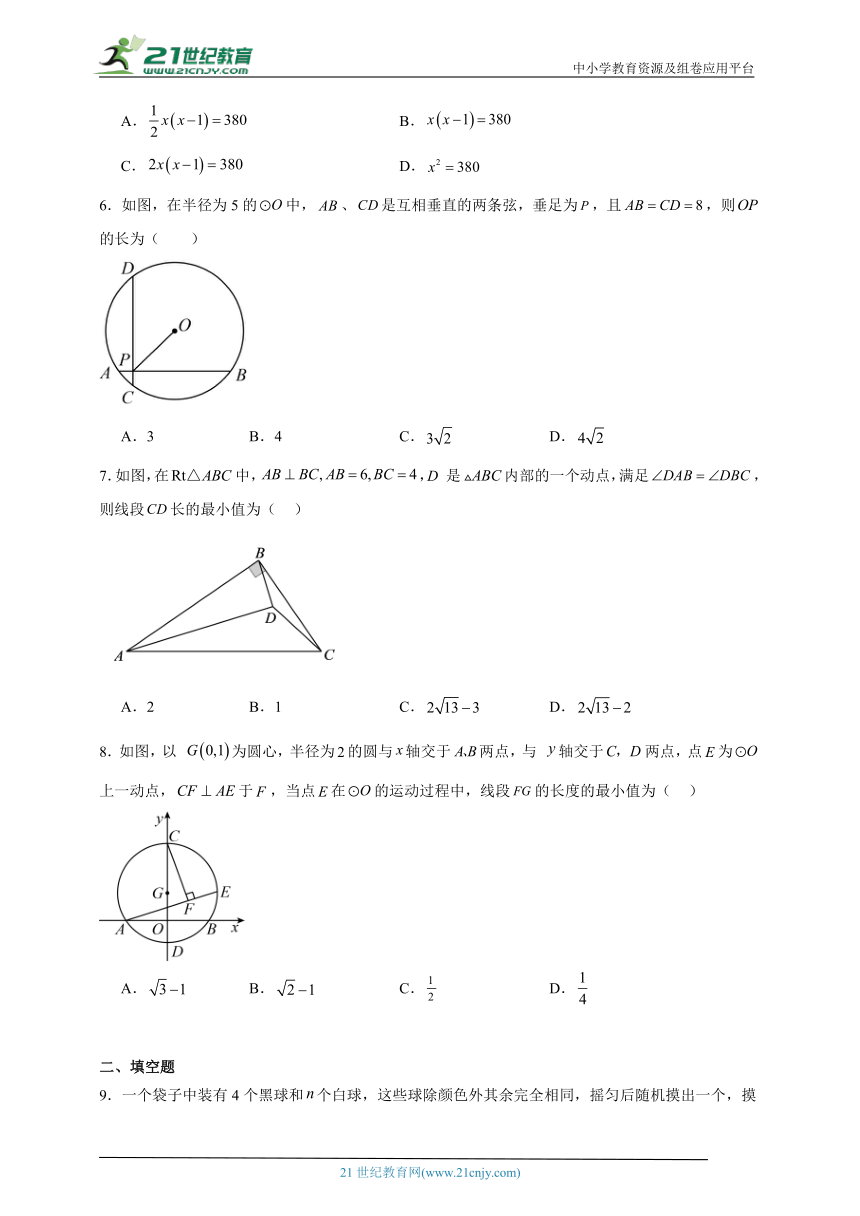
6.如图,在半径为5的中,、是互相垂直的两条弦,垂足为,且,则的长为( )
A.3 B.4 C. D.
7.如图,在中,,D 是内部的一个动点,满足,则线段长的最小值为( )
A.2 B.1 C. D.
8.如图,以 为圆心,半径为的圆与轴交于两点,与 轴交于两点,点为上一动点,于,当点在的运动过程中,线段的长度的最小值为( )
A. B. C. D.
二、填空题
9.一个袋子中装有4个黑球和个白球,这些球除颜色外其余完全相同,摇匀后随机摸出一个,摸到白球的概率为,则白球的个数为 .
10.若是方程的一个根,则代数式的值为 .
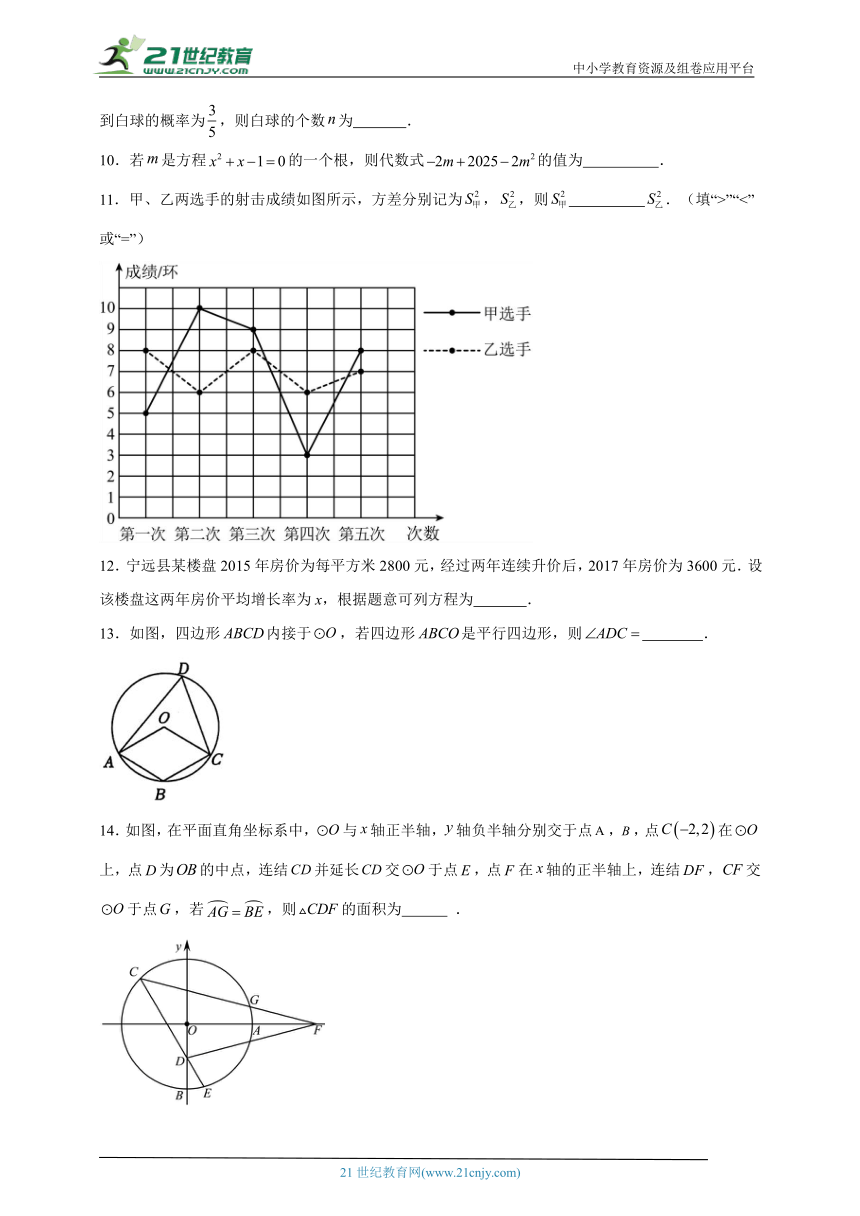
11.甲、乙两选手的射击成绩如图所示,方差分别记为,,则 .(填“>”“<”或“=”)
12.宁远县某楼盘2015年房价为每平方米2800元,经过两年连续升价后,2017年房价为3600元.设该楼盘这两年房价平均增长率为x,根据题意可列方程为 .
13.如图,四边形内接于,若四边形是平行四边形,则 .
14.如图,在平面直角坐标系中,与轴正半轴,轴负半轴分别交于点,,点在上,点为的中点,连结并延长交于点,点在轴的正半轴上,连结,交于点,若,则的面积为 .
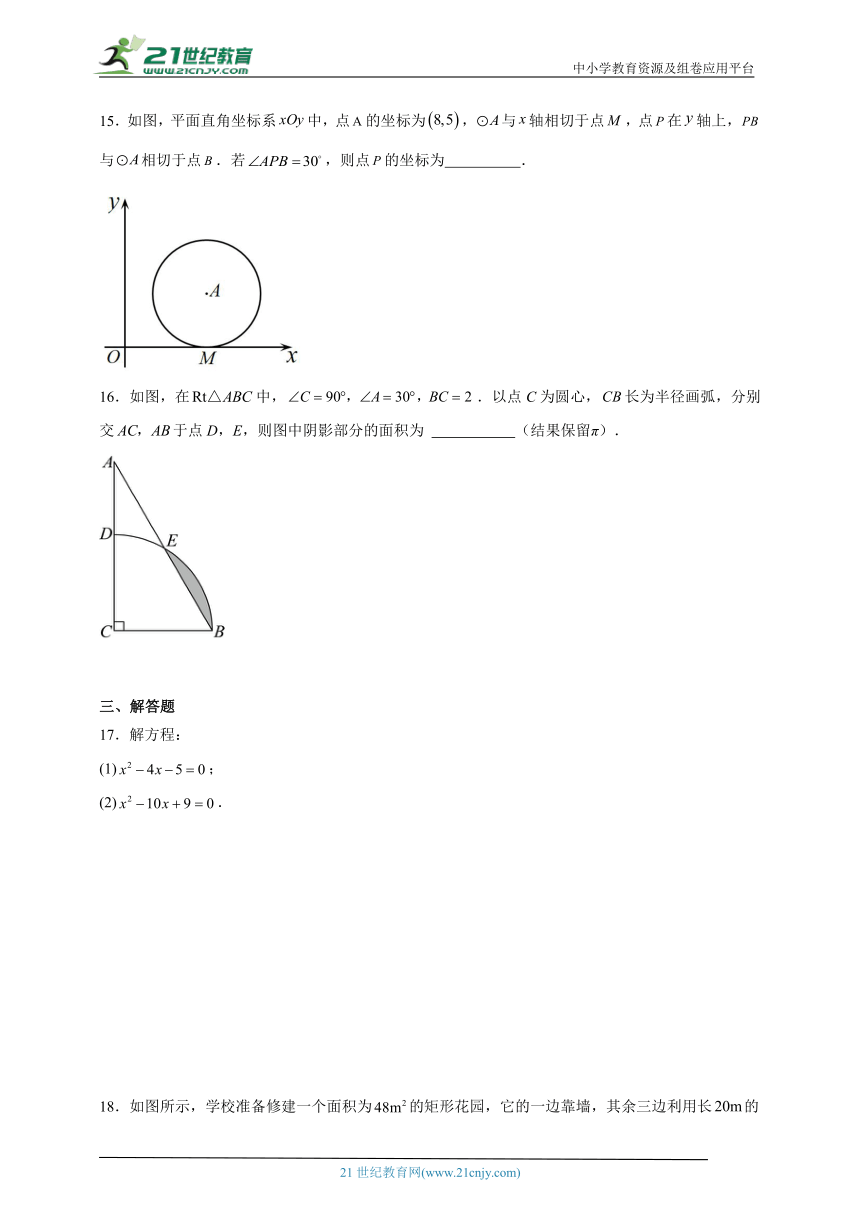
15.如图,平面直角坐标系中,点的坐标为,与轴相切于点,点在轴上,与相切于点.若,则点的坐标为 .
16.如图,在中,.以点C为圆心,长为半径画弧,分别交于点D,E,则图中阴影部分的面积为 (结果保留π).
三、解答题
17.解方程:
(1);
(2).
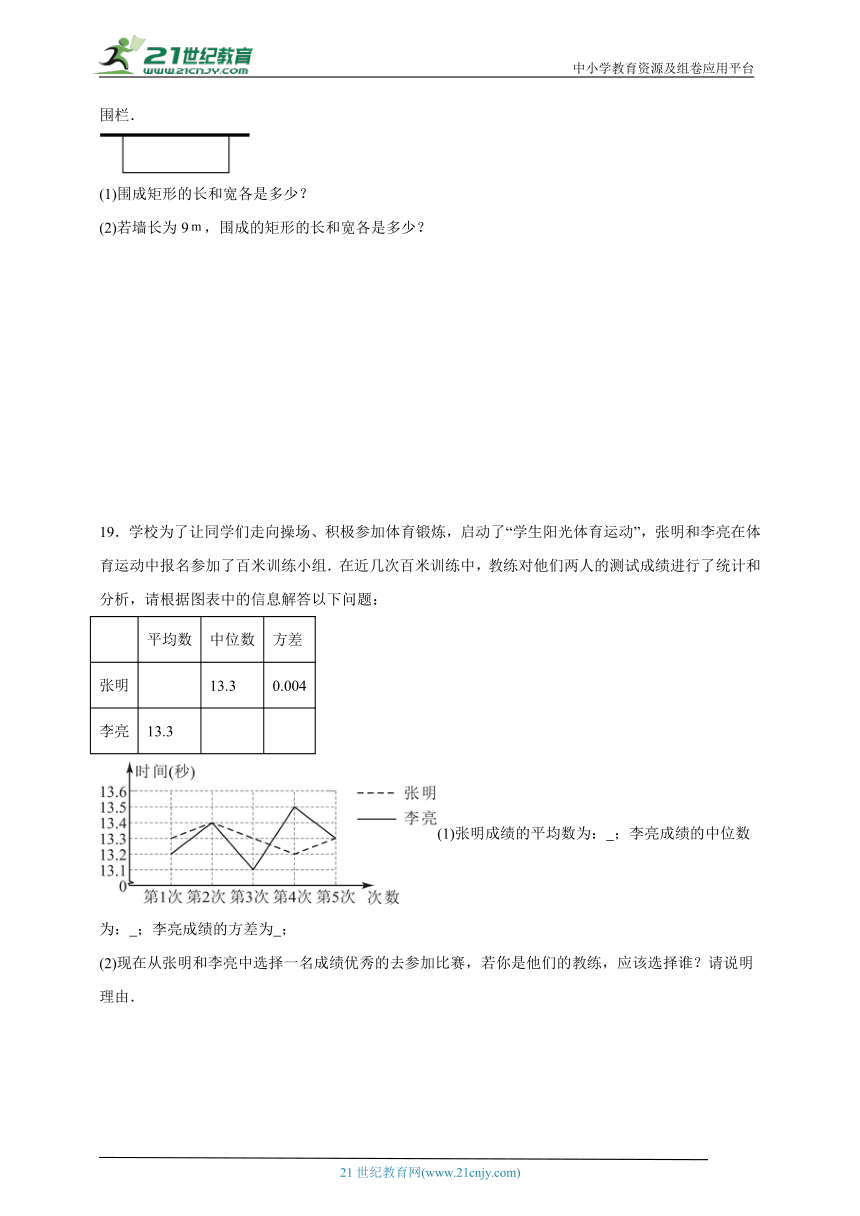
18.如图所示,学校准备修建一个面积为的矩形花园,它的一边靠墙,其余三边利用长的围栏.
(1)围成矩形的长和宽各是多少?
(2)若墙长为9,围成的矩形的长和宽各是多少?
19.学校为了让同学们走向操场、积极参加体育锻炼,启动了“学生阳光体育运动”,张明和李亮在体育运动中报名参加了百米训练小组.在近几次百米训练中,教练对他们两人的测试成绩进行了统计和分析,请根据图表中的信息解答以下问题:
平均数 中位数 方差
张明 13.3 0.004
李亮 13.3
(1)张明成绩的平均数为: ;李亮成绩的中位数为: ;李亮成绩的方差为 ;
(2)现在从张明和李亮中选择一名成绩优秀的去参加比赛,若你是他们的教练,应该选择谁?请说明理由.
20.笼子里关着一只小松鼠(如图),管理员决定把小松鼠放归大自然,将笼子所有的门都打开.松鼠要先经过第一道门(或),再经过第二道门(或或)才能出去.
(1)松鼠经过第一道门时,从口出去的概率是_____;
(2)请用画树状图或列表的方法表示松鼠出笼子的所有可能路线(经过两道门),并求松鼠经过门出去的概率.
21.如图,及外一点.按以下步骤完成作图:
①连接,分别以、为圆心,以大于的长为半径作弧,两弧分别交于、两点(、分别位于直线的上下两侧);
②作直线,交于点;
③以点为圆心,为半径作,交于点(点位于直线的上侧);
④连接,交于点,则直线即为所求.
(1)请按照步骤完成作图,并准确标注字母(尺规作图,保留作图痕迹);
(2)结合图形,判定直线与的位置关系(直接写出结论).
22.如图,平面直角坐标系中,正六边形的顶点、在轴上,顶点在轴上,若,求中心的坐标.
23.每年“双十一”活动,许多网店商家都会进行打折让利的促销活动.甲网店销售一件A商品成本为50元,网上标价为80元.
(1)“双十一”购物活动开始前先打九折预售,问预售价为多少元?
(2)“双十一”购物活动当天,甲网店连续两次降价销售A商品吸引买主,问平均每次降价率为多少,才能使这件A商品的售价为51.2元?
(3)据媒体爆料,有一些商家在“双十一”购物活动当天,先提高商品的网上标价后再推出促销活动,存在欺诈行为:“双十一”活动之前,乙网店销售A商品的成本、网上标价与甲网店一致,一周可售出60件A商品.在“双十一”购物活动这天,乙网店先将网上标价提高a%,再推出5折销售的促销活动,乙网店在“双十一”购物活动当天卖出的A商品数量也比原来一周卖出的A商品数量增加了a%,这样“双十一”活动当天乙网店的利润达到了3600元,求乙网店在“双十一”购物活动这天的网上标价为多少元?
24.石拱桥是我国古代人民勤劳和智慧的结晶(如图①),赵州桥是我国古代石拱桥的代表,图②是根据该石拱桥画出的几何图形,桥的主桥拱是圆弧形,表示为,桥的跨度(弧所对的弦长),设所在圆的圆心为O,,为半径,半径,垂足为D.拱高(弧的中点到弦的距离).
(1)直接写出与的数量关系;
(2)求这座石拱桥主桥拱的半径.
参考答案:
1.B
【分析】本题主要考查加权平均数,根据加权平均数的定义可得答案.解题的关键是掌握加权平均数的定义.
【详解】解:八(3)班的最终成绩是(分),
故选:B.
2.D
【分析】本题考查的是解一元二次方程,直接根据因式分解法求解即可.
【详解】解:,
,
或,
解得.
故选:D.
3.C
【分析】本题主要考查了求样本容量,中位数,众数,平均数,熟练掌握相关定义和求法是解题的关键.
【详解】解:A、该校参与调查的学生有(人),故A不正确,不符合题意;
B、∵该校参与调查的学生有200人,
∴中位数为第100个人和第101个人捐赠书籍的平均数,
由表可知,第100个人和第101个人捐赠书籍均为8本,
∴该校参与调查的学生捐赠书籍的中位数为8本,故B不正确,不符合题意;
C、∵该校参与调查的学生捐赠书籍为8本的人数最多,
∴该校参与调查的学生捐赠书籍的众数为8本,故C正确,符合题意;
D、该校参与调查的学生平均捐赠书籍(本),故D不正确,不符合题意;
故选:C.
4.D
【分析】本题主要考查了求几何概率,先求出空白部分是边长为1的正方形,再根据飞镖落在阴影区域的概率等于阴影部分面积除以这个弦图的面积进行求解即可.
【详解】解:由题意得,空白部分是边长为的正方形,
∴飞镖落在阴影区域的概率为,
故选D.
5.B
【分析】本题考查由实际问题抽象出一元二次方程,关键是设参赛队伍有支,根据参加乒乓球比赛的每两队之间都进行两场比赛,共要比赛380场,可列出方程.
【详解】解:设参赛队伍有x支,
由题意可得:,
故选B.
6.C
【分析】作于,于,连接,,由垂径定理和勾股定理求得,再推出四边形是正方形,求得正方形对角线的长即可得到答案.
【详解】解:作于,于,连接,,
由垂径定理可知,,,
,
由勾股定理得:,,
弦、互相垂直,
,
于,于,
,
四边形是矩形,
,
四边形是正方形,
,
故选:C.
【点睛】本题考查了垂径定理,勾股定理,矩形的和正方形的判定,掌握圆的性质是解题关键.
7.A
【分析】本题考查圆外一点到圆上一点距离的最值问题.根据,推出,得到点在以为直径的圆上,取的中点,连接,,根据,求出最小值即可.解题的关键是确定点的运动轨迹.
【详解】解:∵,
∴,
∴,
∵,
∴,
∴,
∴点在以为直径的圆上,
取的中点,连接,,则:
∵,
∴,
∴,
∴,
∴的最小值为2.
故选A.
8.A
【分析】本题考查垂径定理、直角三角形30度角的判定和性质、勾股定理等知识连接, 作 ,连接,可知点在以为直径的圆上移动,当点在的延长线上时,的长最小,根据含的直角三角形的性质和勾股定理求出,即可求解,解题的关键是学会添加常用辅助线,构造直角三角形解决问题.
【详解】连接, 作 ,连接,
,
∴,
∵为圆心,半径为,
∴,,
在中,,
∴,
∴,,
∵,
∴,
∴
∴,
∴,,
∴,
∵,
∴点在以为直径的圆上移动,
当点在的延长线上时,的长最小,最小值为,
故选:.
9.6
【分析】本题考查利用概率求个数,根据白球概率求出黑球概率,黑球共有4个,就可以求出球的总数,再减去黑球个数即可解答,熟练掌握简单概率公式是解决问题的关键.
【详解】解:∵摇匀后随机摸出一个,摸到白球的概率为,
∴摸到黑球的概率为,
∵袋子中有4个黑球和个白球,
∴由简单概率公式可得,解得,
∴白球有6个,
故答案为:6.
10.
【分析】本题考查一元二次方程的解,根据方程的解满足方程代入方程,再整体代换即可得到答案.
【详解】解:∵是方程的一个根,
∴,
即:,
∴,
故答案为:.
11.>
【分析】本题考查方差的意义.方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
【详解】解:图表数据可知,
甲数据偏离平均数数据较大,乙数据偏离平均数数据较小,
即甲的波动性较大,即方差大,
故答案为:>.
12.
【分析】本题考查了一元二次方程的应用,可得年的价格为每平方米元,进而可求解;掌握增长率的典型模型()的解法是解题的关键.
【详解】解:由题意得
,
故答案:.
13./60度
【分析】本题考查圆内接四边形,圆周角定理,平行四边形的性质,由平行四边形的性质,得,由圆周角定理可知,,可知,在结合内接四边形对角互补可知,即可求解,熟练掌握相关图形的性质是解决问题的关键.
【详解】解:∵四边形是平行四边形,
∴,
由圆周角定理可知,,
则,
又∵四边形是圆的内接四边形,
∴,即:,
∴,
故答案为:.
14.
【分析】本题考查平面直角坐标系中点与线段的长,圆的有关性质,圆周角定理,三角形全等的判定及性质,待定系数法求解析式.
过作,垂足为,过作y轴,交轴于点,过作,垂足为,过作,垂足为,设直线交轴于点,交轴于点.由可得,根据圆周角定理得到,进而求得,,由点可得半径为,从而得到,通过待定系数法求得直线的表达式为,从而得到点,因此,通过“”证明,得到,,因此,又,求得,因此,,即得到,设直线的表达式为,代入点、得直线的表达式为,从而得到点,因此,而,根据三角形的面积公式即可求解.
【详解】过作,垂足为,过作y轴,交轴于点,过作,垂足为,过作,垂足为,设直线交轴于点,交轴于点,
,
,
,
,
∵,
∴,
∴
,
点,
,
,
∵点为的中点,
,
,
设直线的表达式为,代入点得,
∴直线的表达式为,
令得,
∴
,
,,
,
,,
,
,,
,
,
,
,
,
,
,
设直线的表达式为,代入点、得
,
∴,
∴直线的表达式为,
令得,
∴
,
,
.
15.或
【分析】本题考查了圆的切线的性质、矩形的判定和性质、勾股定理等知识,解题关键是把所求的线段放在直角三角形中利用勾股定理求解和已知圆的切线作半径.连接,过点A作轴,利用根据圆的切线性质可知为直角三角形,,利用直角三角形中角的性质和勾股定理分别求出的长度,进而求出的长度即可求得答案.
【详解】解:如图,过点A作轴于点D,连接,
∵轴,轴,
∴四边形为矩形.
∴.
∵与x轴相切,
∴为的半径.
∵点A坐标为,
∴,
∵是切线,
∴.
∵,
∴.
在中,根据勾股定理,得
∴当点P在y轴的正半轴上,则
∴点P坐标为
∴当点P在y轴的负半轴上,则,
∴点P坐标为
综上,点P坐标为或
故答案为:或
16.
【分析】连接,由扇形面积面积求解.本题考查扇形的面积与等边三角形的性质与判定,解题关键是判断出为等边三角形与扇形面积的计算.
【详解】解:连接,
∵,
∴,
∵,
∴为等边三角形,
∴,,
∴,
∵,
∴阴影部分的面积为.
故答案为:
17.(1)
(2)
【分析】本题主要考查了解一元二次方程:
(1)利用因式分解法解方程即可;
(2)利用因式分解法解方程即可.
【详解】(1)解:
,
或,
解得;
(2)解:
,
或,
解得.
18.(1)长为8、宽为6或长12,宽4
(2)矩形长8,宽6
【分析】本题主要考查一元二次方程的应用,
设宽为,则长为.利用面积列出一元二次方程,解方程即可;
结合矩形的长不能大于9,即可得到矩形的长宽.
【详解】(1)解:设宽为,则长为.
由题意,得,
解得,,
那么,当时,,
当时,.
答:围成矩形的长为8、宽为6或长12,宽4;
(2)由(1)得,若墙长9米,12大于9,舍去,围成的矩形长8,宽6.
19.(1)13.3,13.3,0.02
(2)选择张明参加比赛,理由见解析
【分析】本题考查了平均数,中位数,方差的意义:
(1)利用平均数的计算公式可得出张明成绩的平均数;先将李亮的成绩按照从小到大排列,然后即可得到这组数据的中位数;
(2)在平均数、中位数相同的情况下,再根据方差越小数据越稳定,即可得出答案.
【详解】(1)解:张明成绩的平均数为:(秒);
李亮的成绩是:13.2,13.4,13.1,13.5,13.3,
把这些数从小到大排列为:13.1,13.2,13.3,13.4,13.5,
则李亮成绩的中位数是:13.3秒;
李亮的方差为:
故答案为:13.3,13.3,0.02;
(2)解: 选择张明参加比赛,理由如下:
因为张明和李亮成绩的平均数、中位数都相同,但张明成绩的方差小于李亮成绩的方差,张明成绩比李亮成绩稳定.
20.(1)
(2)
【分析】本题考查了概率的应用,掌握概率的求解方法以及画树状图或列表法是解题关键.
(1)根据松鼠经过第一道门时,要么选择,要么选择,即可求解;
(2)根据题意画出树状图,找出总的可能情况和松鼠经过门出去的情况,即可求出概率.
【详解】(1)解:∵松鼠经过第一道门时,要么选择,要么选择,
∴松鼠经过第一道门时,从口出去的概率是,
故答案为:
(2)解:画树状图如下:
共有6种等可能的情况,其中松鼠经过门出去的情况有2种,
∴松鼠经过门出去的概率是
21.(1)见解析
(2)直线与相切
【分析】本题考查尺规作图,切线的判定,直径所对的圆周角为.
(1)按照步骤即可完成作图;
(2)直线与相切,理由是由是的直径可得,即,又是的半径,即可判定直线与的切线.
【详解】(1)所求图形,如图所示
(2)连接,
∵是的直径,
∴,即,
∵是的半径,
∴直线与相切.
22.
【分析】本题考查了正多边形的性质,勾股定理,平面直角坐标系等知识,连接、,过点P作轴于Q,证明是等边三角形,求出,然后利用含的直角三角形的性质求出、,利用勾股定理求出,即可求解.
【详解】解:连接、,过点P作轴于Q,
∵六边形是正六边形,,
∴,,,,
∴,是等边三角形,,
∴,,,
∴,
∴,
∴中心的坐标为.
23.(1)预售价为72元.
(2)平均每次降价率为20%,才能使这件A商品的售价为51.2元.
(3)乙网店在“双十一”购物活动这天的网上标价为160元.
【分析】本题考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的关键.
(1)根据“售价=标价×折扣”即可求解;
(2)设平均每次降价率为x,建立方程即可求解;
(3)首先列出方程求出增长率,再求得标价即可;
【详解】(1)解:(元).
答:预售价为72元.
(2)设平均每次降价率为x,
依题意,得:,
解得:,(不合题意,舍去).
答:平均每次降价率为20%,才能使这件A商品的售价为51.2元.
(3)依题意,得:,
整理,得:,
解得:,(不合题意,舍去),
∴.
答:乙网店在“双十一”购物活动这天的网上标价为160元.
24.(1)
(2)这座石拱桥主桥拱半径约为
【分析】此题考查垂径定理和勾股定理,是重要考点,根据题意利用勾股定理列出方程是解题关键.
(1)根据垂径定理即可得出结论;
(2)设主桥拱半径为,在中,根据勾股定理列出方程,即可得出答案.
【详解】(1)解:∵半径,
∴.
(2)解:设主桥拱半径为,
∵,,,
∴,,
在中,由勾股定理,得,
即,
解得,
因此,这座石拱桥主桥拱半径约为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末易错精选题检测卷-2023-2024学年数学九年级上册苏科版
一、单选题
1.在学校举办的合唱比赛中,八(3)班的演唱质量、精神风貌、配合默契得分分别为92分,80分,70分,若最终成绩由这三项得分依次按照 ,,的百分比确定,则八(3)班的最终成绩是 ( )
A.80.6分 B.81.8分 C.84.7分 D.96.8分
2.一元二次方程的根是( )
A.0 B.2 C.0,2 D.1,2
3.某校发起了“圆贫困地区孩子一个读书梦”的爱心捐书公益活动,在短短一周时间内,就收到了同学们捐赠的大量书籍. 现从中随机调查了部分学生的捐赠情况,并将收集到的数据统计如下:
数量/本 30 22 16 8 6 4
人数 40 30 25 50 20 35
根据表中的信息判断,下列结论正确的是( )
A.该校参与调查的学生有86人
B.该校参与调查的学生捐赠书籍的中位数为12本
C.该校参与调查的学生捐赠书籍的众数为8本
D.该校参与调查的学生平均捐赠书籍16本
4.汉代数学家赵爽在注解《周髀算经》时,给出的“赵爽弦图”是我国古代数学的瑰宝.如图,这个弦图中的四个直角三角形都是全等的,它们的两直角边的长分别是2和3.现随机向该图形内掷一枚飞镖,则飞镖落在阴影区域的概率为( )
A. B. C. D.
5.10月8日,杭州亚运会乒乓球比赛全部结束,国乒揽获除女双项目外的6块金牌,展现了在乒乓球领域强大的统治力.乒乓球比赛采用双循环制(每两队之间都进行两场比赛),比赛总场数为380场,若设参赛队伍有x支,则可列方程为( )
A. B.
C. D.
6.如图,在半径为5的中,、是互相垂直的两条弦,垂足为,且,则的长为( )
A.3 B.4 C. D.
7.如图,在中,,D 是内部的一个动点,满足,则线段长的最小值为( )
A.2 B.1 C. D.
8.如图,以 为圆心,半径为的圆与轴交于两点,与 轴交于两点,点为上一动点,于,当点在的运动过程中,线段的长度的最小值为( )
A. B. C. D.
二、填空题
9.一个袋子中装有4个黑球和个白球,这些球除颜色外其余完全相同,摇匀后随机摸出一个,摸到白球的概率为,则白球的个数为 .
10.若是方程的一个根,则代数式的值为 .
11.甲、乙两选手的射击成绩如图所示,方差分别记为,,则 .(填“>”“<”或“=”)
12.宁远县某楼盘2015年房价为每平方米2800元,经过两年连续升价后,2017年房价为3600元.设该楼盘这两年房价平均增长率为x,根据题意可列方程为 .
13.如图,四边形内接于,若四边形是平行四边形,则 .
14.如图,在平面直角坐标系中,与轴正半轴,轴负半轴分别交于点,,点在上,点为的中点,连结并延长交于点,点在轴的正半轴上,连结,交于点,若,则的面积为 .
15.如图,平面直角坐标系中,点的坐标为,与轴相切于点,点在轴上,与相切于点.若,则点的坐标为 .
16.如图,在中,.以点C为圆心,长为半径画弧,分别交于点D,E,则图中阴影部分的面积为 (结果保留π).
三、解答题
17.解方程:
(1);
(2).
18.如图所示,学校准备修建一个面积为的矩形花园,它的一边靠墙,其余三边利用长的围栏.
(1)围成矩形的长和宽各是多少?
(2)若墙长为9,围成的矩形的长和宽各是多少?
19.学校为了让同学们走向操场、积极参加体育锻炼,启动了“学生阳光体育运动”,张明和李亮在体育运动中报名参加了百米训练小组.在近几次百米训练中,教练对他们两人的测试成绩进行了统计和分析,请根据图表中的信息解答以下问题:
平均数 中位数 方差
张明 13.3 0.004
李亮 13.3
(1)张明成绩的平均数为: ;李亮成绩的中位数为: ;李亮成绩的方差为 ;
(2)现在从张明和李亮中选择一名成绩优秀的去参加比赛,若你是他们的教练,应该选择谁?请说明理由.
20.笼子里关着一只小松鼠(如图),管理员决定把小松鼠放归大自然,将笼子所有的门都打开.松鼠要先经过第一道门(或),再经过第二道门(或或)才能出去.
(1)松鼠经过第一道门时,从口出去的概率是_____;
(2)请用画树状图或列表的方法表示松鼠出笼子的所有可能路线(经过两道门),并求松鼠经过门出去的概率.
21.如图,及外一点.按以下步骤完成作图:
①连接,分别以、为圆心,以大于的长为半径作弧,两弧分别交于、两点(、分别位于直线的上下两侧);
②作直线,交于点;
③以点为圆心,为半径作,交于点(点位于直线的上侧);
④连接,交于点,则直线即为所求.
(1)请按照步骤完成作图,并准确标注字母(尺规作图,保留作图痕迹);
(2)结合图形,判定直线与的位置关系(直接写出结论).
22.如图,平面直角坐标系中,正六边形的顶点、在轴上,顶点在轴上,若,求中心的坐标.
23.每年“双十一”活动,许多网店商家都会进行打折让利的促销活动.甲网店销售一件A商品成本为50元,网上标价为80元.
(1)“双十一”购物活动开始前先打九折预售,问预售价为多少元?
(2)“双十一”购物活动当天,甲网店连续两次降价销售A商品吸引买主,问平均每次降价率为多少,才能使这件A商品的售价为51.2元?
(3)据媒体爆料,有一些商家在“双十一”购物活动当天,先提高商品的网上标价后再推出促销活动,存在欺诈行为:“双十一”活动之前,乙网店销售A商品的成本、网上标价与甲网店一致,一周可售出60件A商品.在“双十一”购物活动这天,乙网店先将网上标价提高a%,再推出5折销售的促销活动,乙网店在“双十一”购物活动当天卖出的A商品数量也比原来一周卖出的A商品数量增加了a%,这样“双十一”活动当天乙网店的利润达到了3600元,求乙网店在“双十一”购物活动这天的网上标价为多少元?
24.石拱桥是我国古代人民勤劳和智慧的结晶(如图①),赵州桥是我国古代石拱桥的代表,图②是根据该石拱桥画出的几何图形,桥的主桥拱是圆弧形,表示为,桥的跨度(弧所对的弦长),设所在圆的圆心为O,,为半径,半径,垂足为D.拱高(弧的中点到弦的距离).
(1)直接写出与的数量关系;
(2)求这座石拱桥主桥拱的半径.
参考答案:
1.B
【分析】本题主要考查加权平均数,根据加权平均数的定义可得答案.解题的关键是掌握加权平均数的定义.
【详解】解:八(3)班的最终成绩是(分),
故选:B.
2.D
【分析】本题考查的是解一元二次方程,直接根据因式分解法求解即可.
【详解】解:,
,
或,
解得.
故选:D.
3.C
【分析】本题主要考查了求样本容量,中位数,众数,平均数,熟练掌握相关定义和求法是解题的关键.
【详解】解:A、该校参与调查的学生有(人),故A不正确,不符合题意;
B、∵该校参与调查的学生有200人,
∴中位数为第100个人和第101个人捐赠书籍的平均数,
由表可知,第100个人和第101个人捐赠书籍均为8本,
∴该校参与调查的学生捐赠书籍的中位数为8本,故B不正确,不符合题意;
C、∵该校参与调查的学生捐赠书籍为8本的人数最多,
∴该校参与调查的学生捐赠书籍的众数为8本,故C正确,符合题意;
D、该校参与调查的学生平均捐赠书籍(本),故D不正确,不符合题意;
故选:C.
4.D
【分析】本题主要考查了求几何概率,先求出空白部分是边长为1的正方形,再根据飞镖落在阴影区域的概率等于阴影部分面积除以这个弦图的面积进行求解即可.
【详解】解:由题意得,空白部分是边长为的正方形,
∴飞镖落在阴影区域的概率为,
故选D.
5.B
【分析】本题考查由实际问题抽象出一元二次方程,关键是设参赛队伍有支,根据参加乒乓球比赛的每两队之间都进行两场比赛,共要比赛380场,可列出方程.
【详解】解:设参赛队伍有x支,
由题意可得:,
故选B.
6.C
【分析】作于,于,连接,,由垂径定理和勾股定理求得,再推出四边形是正方形,求得正方形对角线的长即可得到答案.
【详解】解:作于,于,连接,,
由垂径定理可知,,,
,
由勾股定理得:,,
弦、互相垂直,
,
于,于,
,
四边形是矩形,
,
四边形是正方形,
,
故选:C.
【点睛】本题考查了垂径定理,勾股定理,矩形的和正方形的判定,掌握圆的性质是解题关键.
7.A
【分析】本题考查圆外一点到圆上一点距离的最值问题.根据,推出,得到点在以为直径的圆上,取的中点,连接,,根据,求出最小值即可.解题的关键是确定点的运动轨迹.
【详解】解:∵,
∴,
∴,
∵,
∴,
∴,
∴点在以为直径的圆上,
取的中点,连接,,则:
∵,
∴,
∴,
∴,
∴的最小值为2.
故选A.
8.A
【分析】本题考查垂径定理、直角三角形30度角的判定和性质、勾股定理等知识连接, 作 ,连接,可知点在以为直径的圆上移动,当点在的延长线上时,的长最小,根据含的直角三角形的性质和勾股定理求出,即可求解,解题的关键是学会添加常用辅助线,构造直角三角形解决问题.
【详解】连接, 作 ,连接,
,
∴,
∵为圆心,半径为,
∴,,
在中,,
∴,
∴,,
∵,
∴,
∴
∴,
∴,,
∴,
∵,
∴点在以为直径的圆上移动,
当点在的延长线上时,的长最小,最小值为,
故选:.
9.6
【分析】本题考查利用概率求个数,根据白球概率求出黑球概率,黑球共有4个,就可以求出球的总数,再减去黑球个数即可解答,熟练掌握简单概率公式是解决问题的关键.
【详解】解:∵摇匀后随机摸出一个,摸到白球的概率为,
∴摸到黑球的概率为,
∵袋子中有4个黑球和个白球,
∴由简单概率公式可得,解得,
∴白球有6个,
故答案为:6.
10.
【分析】本题考查一元二次方程的解,根据方程的解满足方程代入方程,再整体代换即可得到答案.
【详解】解:∵是方程的一个根,
∴,
即:,
∴,
故答案为:.
11.>
【分析】本题考查方差的意义.方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
【详解】解:图表数据可知,
甲数据偏离平均数数据较大,乙数据偏离平均数数据较小,
即甲的波动性较大,即方差大,
故答案为:>.
12.
【分析】本题考查了一元二次方程的应用,可得年的价格为每平方米元,进而可求解;掌握增长率的典型模型()的解法是解题的关键.
【详解】解:由题意得
,
故答案:.
13./60度
【分析】本题考查圆内接四边形,圆周角定理,平行四边形的性质,由平行四边形的性质,得,由圆周角定理可知,,可知,在结合内接四边形对角互补可知,即可求解,熟练掌握相关图形的性质是解决问题的关键.
【详解】解:∵四边形是平行四边形,
∴,
由圆周角定理可知,,
则,
又∵四边形是圆的内接四边形,
∴,即:,
∴,
故答案为:.
14.
【分析】本题考查平面直角坐标系中点与线段的长,圆的有关性质,圆周角定理,三角形全等的判定及性质,待定系数法求解析式.
过作,垂足为,过作y轴,交轴于点,过作,垂足为,过作,垂足为,设直线交轴于点,交轴于点.由可得,根据圆周角定理得到,进而求得,,由点可得半径为,从而得到,通过待定系数法求得直线的表达式为,从而得到点,因此,通过“”证明,得到,,因此,又,求得,因此,,即得到,设直线的表达式为,代入点、得直线的表达式为,从而得到点,因此,而,根据三角形的面积公式即可求解.
【详解】过作,垂足为,过作y轴,交轴于点,过作,垂足为,过作,垂足为,设直线交轴于点,交轴于点,
,
,
,
,
∵,
∴,
∴
,
点,
,
,
∵点为的中点,
,
,
设直线的表达式为,代入点得,
∴直线的表达式为,
令得,
∴
,
,,
,
,,
,
,,
,
,
,
,
,
,
,
设直线的表达式为,代入点、得
,
∴,
∴直线的表达式为,
令得,
∴
,
,
.
15.或
【分析】本题考查了圆的切线的性质、矩形的判定和性质、勾股定理等知识,解题关键是把所求的线段放在直角三角形中利用勾股定理求解和已知圆的切线作半径.连接,过点A作轴,利用根据圆的切线性质可知为直角三角形,,利用直角三角形中角的性质和勾股定理分别求出的长度,进而求出的长度即可求得答案.
【详解】解:如图,过点A作轴于点D,连接,
∵轴,轴,
∴四边形为矩形.
∴.
∵与x轴相切,
∴为的半径.
∵点A坐标为,
∴,
∵是切线,
∴.
∵,
∴.
在中,根据勾股定理,得
∴当点P在y轴的正半轴上,则
∴点P坐标为
∴当点P在y轴的负半轴上,则,
∴点P坐标为
综上,点P坐标为或
故答案为:或
16.
【分析】连接,由扇形面积面积求解.本题考查扇形的面积与等边三角形的性质与判定,解题关键是判断出为等边三角形与扇形面积的计算.
【详解】解:连接,
∵,
∴,
∵,
∴为等边三角形,
∴,,
∴,
∵,
∴阴影部分的面积为.
故答案为:
17.(1)
(2)
【分析】本题主要考查了解一元二次方程:
(1)利用因式分解法解方程即可;
(2)利用因式分解法解方程即可.
【详解】(1)解:
,
或,
解得;
(2)解:
,
或,
解得.
18.(1)长为8、宽为6或长12,宽4
(2)矩形长8,宽6
【分析】本题主要考查一元二次方程的应用,
设宽为,则长为.利用面积列出一元二次方程,解方程即可;
结合矩形的长不能大于9,即可得到矩形的长宽.
【详解】(1)解:设宽为,则长为.
由题意,得,
解得,,
那么,当时,,
当时,.
答:围成矩形的长为8、宽为6或长12,宽4;
(2)由(1)得,若墙长9米,12大于9,舍去,围成的矩形长8,宽6.
19.(1)13.3,13.3,0.02
(2)选择张明参加比赛,理由见解析
【分析】本题考查了平均数,中位数,方差的意义:
(1)利用平均数的计算公式可得出张明成绩的平均数;先将李亮的成绩按照从小到大排列,然后即可得到这组数据的中位数;
(2)在平均数、中位数相同的情况下,再根据方差越小数据越稳定,即可得出答案.
【详解】(1)解:张明成绩的平均数为:(秒);
李亮的成绩是:13.2,13.4,13.1,13.5,13.3,
把这些数从小到大排列为:13.1,13.2,13.3,13.4,13.5,
则李亮成绩的中位数是:13.3秒;
李亮的方差为:
故答案为:13.3,13.3,0.02;
(2)解: 选择张明参加比赛,理由如下:
因为张明和李亮成绩的平均数、中位数都相同,但张明成绩的方差小于李亮成绩的方差,张明成绩比李亮成绩稳定.
20.(1)
(2)
【分析】本题考查了概率的应用,掌握概率的求解方法以及画树状图或列表法是解题关键.
(1)根据松鼠经过第一道门时,要么选择,要么选择,即可求解;
(2)根据题意画出树状图,找出总的可能情况和松鼠经过门出去的情况,即可求出概率.
【详解】(1)解:∵松鼠经过第一道门时,要么选择,要么选择,
∴松鼠经过第一道门时,从口出去的概率是,
故答案为:
(2)解:画树状图如下:
共有6种等可能的情况,其中松鼠经过门出去的情况有2种,
∴松鼠经过门出去的概率是
21.(1)见解析
(2)直线与相切
【分析】本题考查尺规作图,切线的判定,直径所对的圆周角为.
(1)按照步骤即可完成作图;
(2)直线与相切,理由是由是的直径可得,即,又是的半径,即可判定直线与的切线.
【详解】(1)所求图形,如图所示
(2)连接,
∵是的直径,
∴,即,
∵是的半径,
∴直线与相切.
22.
【分析】本题考查了正多边形的性质,勾股定理,平面直角坐标系等知识,连接、,过点P作轴于Q,证明是等边三角形,求出,然后利用含的直角三角形的性质求出、,利用勾股定理求出,即可求解.
【详解】解:连接、,过点P作轴于Q,
∵六边形是正六边形,,
∴,,,,
∴,是等边三角形,,
∴,,,
∴,
∴,
∴中心的坐标为.
23.(1)预售价为72元.
(2)平均每次降价率为20%,才能使这件A商品的售价为51.2元.
(3)乙网店在“双十一”购物活动这天的网上标价为160元.
【分析】本题考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的关键.
(1)根据“售价=标价×折扣”即可求解;
(2)设平均每次降价率为x,建立方程即可求解;
(3)首先列出方程求出增长率,再求得标价即可;
【详解】(1)解:(元).
答:预售价为72元.
(2)设平均每次降价率为x,
依题意,得:,
解得:,(不合题意,舍去).
答:平均每次降价率为20%,才能使这件A商品的售价为51.2元.
(3)依题意,得:,
整理,得:,
解得:,(不合题意,舍去),
∴.
答:乙网店在“双十一”购物活动这天的网上标价为160元.
24.(1)
(2)这座石拱桥主桥拱半径约为
【分析】此题考查垂径定理和勾股定理,是重要考点,根据题意利用勾股定理列出方程是解题关键.
(1)根据垂径定理即可得出结论;
(2)设主桥拱半径为,在中,根据勾股定理列出方程,即可得出答案.
【详解】(1)解:∵半径,
∴.
(2)解:设主桥拱半径为,
∵,,,
∴,,
在中,由勾股定理,得,
即,
解得,
因此,这座石拱桥主桥拱半径约为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
