数学人教A版(2019)选择性必修第一册第一章 空间向量与立体几何章末复习 课件(共39张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册第一章 空间向量与立体几何章末复习 课件(共39张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 5.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-17 07:06:13 | ||
图片预览



文档简介
(共39张PPT)
空间向量与立体几何复习
选择性必修第一册 第一章 《空间向量与立体几何》
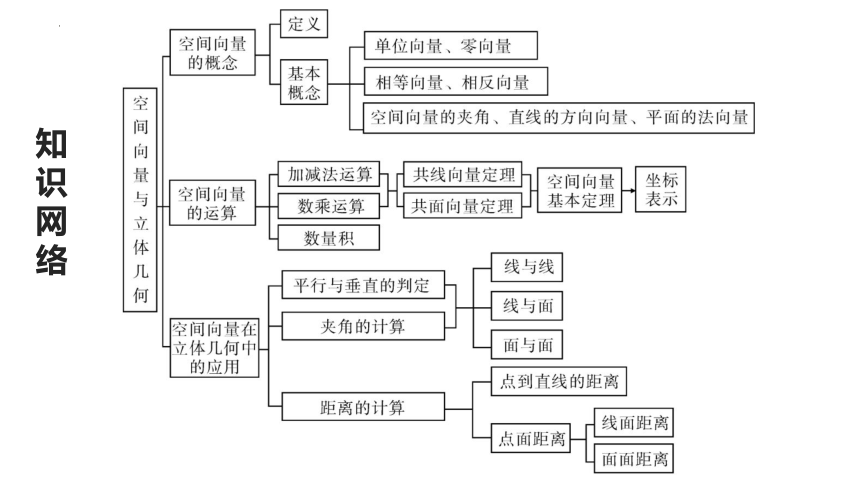
知识网络
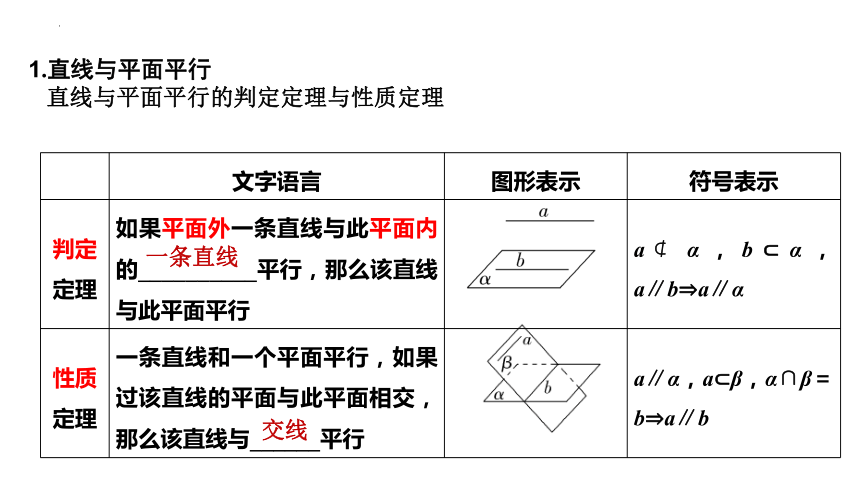
1.直线与平面平行
直线与平面平行的判定定理与性质定理
文字语言 图形表示 符号表示
判定定理 如果平面外一条直线与此平面内的__________平行,那么该直线与此平面平行 a α,b α,a∥b a∥α
性质定理 一条直线和一个平面平行,如果过该直线的平面与此平面相交,那么该直线与______平行 a∥α,a β,α∩β=b a∥b
一条直线
交线
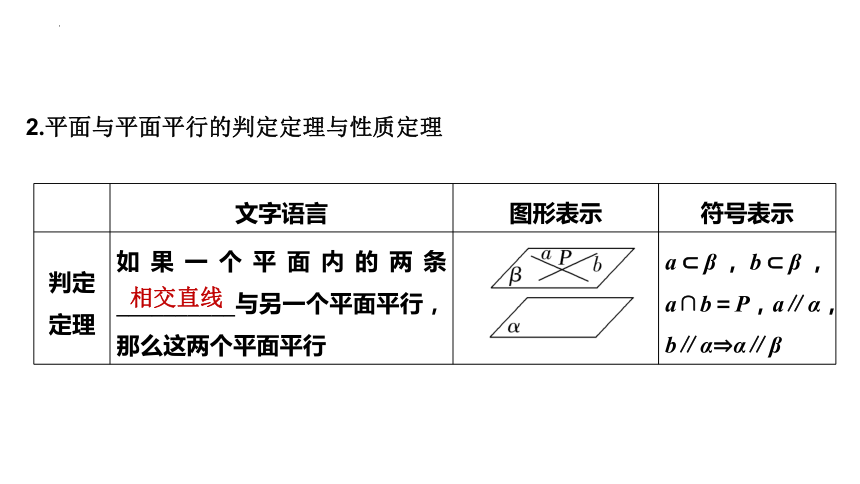
2.平面与平面平行的判定定理与性质定理
文字语言 图形表示 符号表示
判定定理 如果一个平面内的两条__________与另一个平面平行,那么这两个平面平行 a β,b β,a∩b=P,a∥α,b∥α α∥β
相交直线
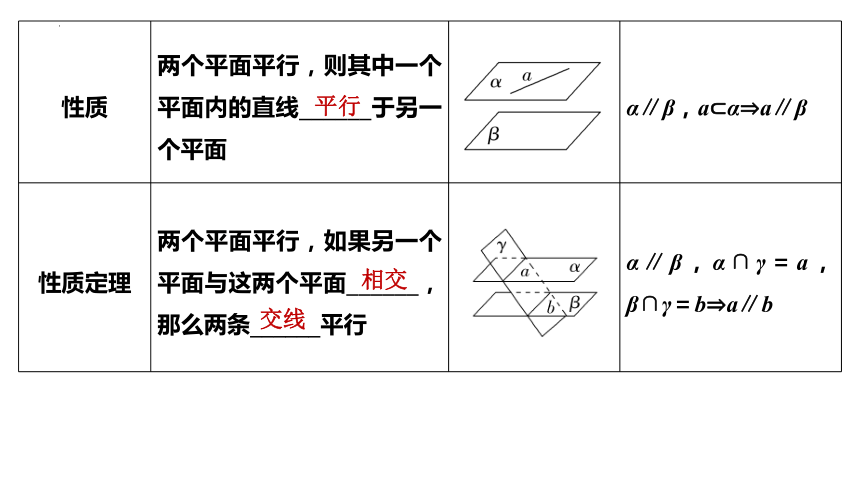
性质 两个平面平行,则其中一个平面内的直线______于另一个平面 α∥β,a α a∥β
性质定理 两个平面平行,如果另一个平面与这两个平面______,那么两条______平行 α∥β,α∩γ=a,β∩γ=b a∥b
平行
相交
交线
1.平行关系中的三个重要结论
(1)垂直于同一条直线的两个平面平行,即若a⊥α,a⊥β,则α∥β.
(2)平行于同一平面的两个平面平行,即若α∥β,β∥γ,则α∥γ.
(3)垂直于同一个平面的两条直线平行,即若a⊥α,b⊥α,则a∥b.
2.三种平行关系的转化
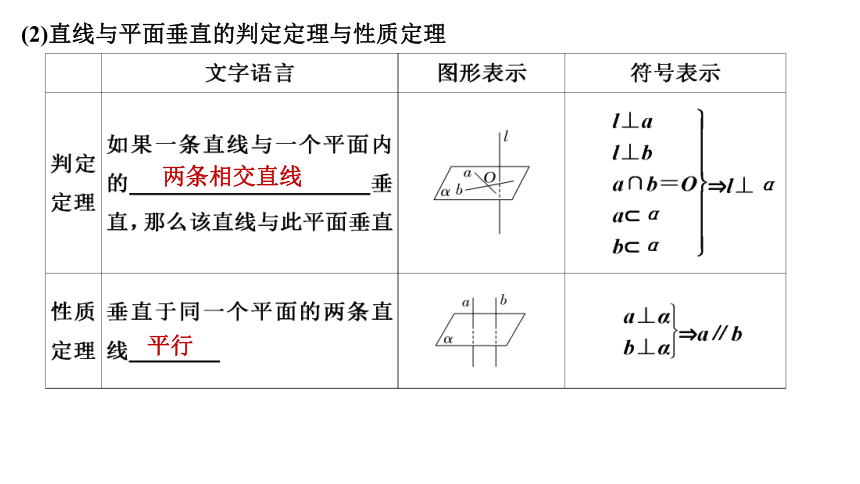
(2)直线与平面垂直的判定定理与性质定理
两条相交直线
平行
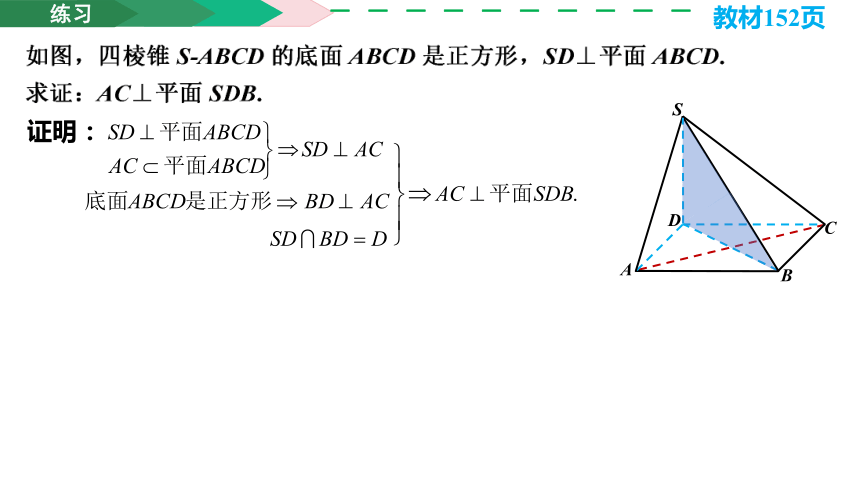
练习
- - - - - - - - - -
教材152页
证明:
B
D
C
S
A
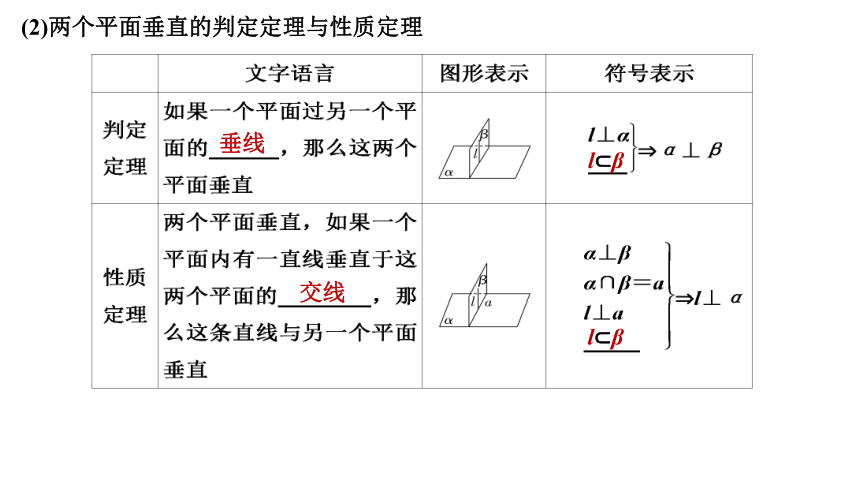
(2)两个平面垂直的判定定理与性质定理
垂线
l β
交线
l β
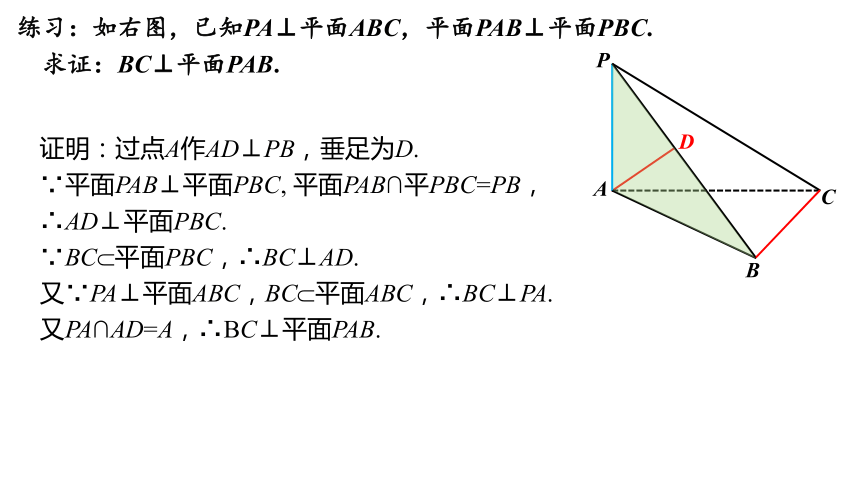
练习:如右图,已知PA⊥平面ABC,平面PAB⊥平面PBC.
求证:BC⊥平面PAB.
D
证明:过点A作AD⊥PB,垂足为D.
∵平面PAB⊥平面PBC, 平面PAB∩平PBC=PB,
∴AD⊥平面PBC.
∵BC 平面PBC,∴BC⊥AD.
又∵PA⊥平面ABC,BC 平面ABC,∴BC⊥PA.
又PA∩AD=A,∴BC⊥平面PAB.
P
A
B
C
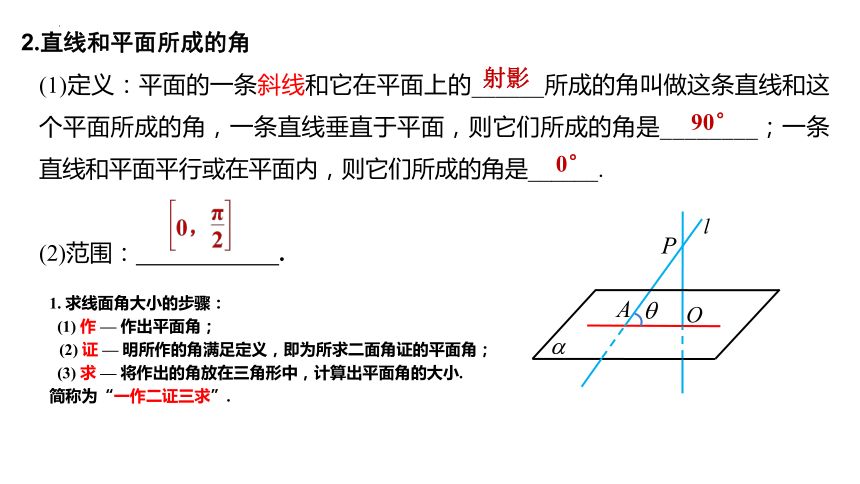
2.直线和平面所成的角
(1)定义:平面的一条斜线和它在平面上的______所成的角叫做这条直线和这个平面所成的角,一条直线垂直于平面,则它们所成的角是________;一条直线和平面平行或在平面内,则它们所成的角是______.
(2)范围: .
射影
90°
0°
1. 求线面角大小的步骤:
(1) 作 — 作出平面角;
(2) 证 — 明所作的角满足定义,即为所求二面角证的平面角;
(3) 求 — 将作出的角放在三角形中,计算出平面角的大小.
简称为“一作二证三求”.
C
A
M
B
3.二面角
(1)定义:从一条直线出发的____________所组成的图形叫做二面角.
(2)二面角的平面角
若有①O∈l;②OA α,OB β;③OA⊥l,OB⊥l,则二面角α-l-β的平面角是__________.
(3)二面角的平面角α的范围:[0,π].
两个半平面
∠AOB
4. 平面与平面的夹角的定义:平面α与平面β相交所形成的4个二面角中,把其中不大于90°的二面角称为平面α与平面β的夹角.
1. 求二面角大小的步骤:
(1) 作 — 作出平面角;
(2) 证 — 明所作的角满足定义,即为所求二面角证的平面角;
(3) 求 — 将作出的角放在三角形中,计算出平面角的大小.
简称为“一作二证三求”.
2. 作出二面角的平面角的方法:
方法一:(定义法) 在二面角的棱上找一个特殊点O,在两个半平面内分别作垂直于棱的射线OA,OB.
如图所示,∠AOB为二面角α- a -β的平面角.
练习:如右图,已知PA⊥平面ABC, BC⊥AB.
求平面ABC与平面PBC所成的二面角的平面角.
D
P
A
B
C
O
A
B
1.找角:两向量同起点
2.范围:
3.求角:
4.向量夹角与数量积的关系:
5. 投影向量:
1.共线向量定理:对于任意两个空间向量 ,
①作用:判定两个向量是否共线(找λ).
②推论:判定三点是否共线(同起点&系数和为1;或转化为向量共线).
2. 共面向量定理:
作用: 判定三个向量是否共面(找x,y).
推论: 判定四点是否共面(同起点/系数和为1,或转化为三个向量共面).
1.直线的方向向量:直线的方向向量是指和这条直线平行(或在这条直线上)的有向线段所表示的向量,一条直线的方向向量有无数个.
2.平面的法向量:直线l⊥平面α,取直线l的方向向量,则这个向量叫做平面α的法向量.显然一个平面的法向量有无数个,它们是共线向量.
位置关系 向量表示 直线l1,l2的方向向量分别为n1,n2 l1∥l2 n1∥n2 n1=λn2
l1⊥l2 n1⊥n2 n1·n2=0
直线l的方向向量为n, 平面α的法向量为m l∥α n⊥m n·m=0
l⊥α n∥m n=λm
平面α,β的法向量分别为n,m α∥β n∥m n=λm
α⊥β n⊥m n·m=0
2.利用空间向量的坐标运算求夹角或距离的一般步骤
(1)建系:根据题目中的几何图形建立恰当的空间直角坐标系;
(2)求坐标:①求出相关点的坐标;②写出向量的坐标;
(3)坐标运算:结合公式进行计算、论证;
(4)翻译:将坐标运算的结果翻译为夹角或距离等集合语言.
②等面积法(将点线距离视为三角形的高)
两条平行直线m,l间的距离转化为直线m上任一点到直线l的距离
4.2求直线到直线的距离:
4.1求点到直线的距离:
4.3求点到平面的距离:
①等体积法(将点面距离看作三棱锥的高)
③找垂线法(过点找面的垂线)
平行于平面的直线到平面的距离转化为线上任意一点到平面的距离
两个平行平面间的距离转化为平面内任意一点到平面的距离
空间向量与立体几何复习
选择性必修第一册 第一章 《空间向量与立体几何》
知识网络
1.直线与平面平行
直线与平面平行的判定定理与性质定理
文字语言 图形表示 符号表示
判定定理 如果平面外一条直线与此平面内的__________平行,那么该直线与此平面平行 a α,b α,a∥b a∥α
性质定理 一条直线和一个平面平行,如果过该直线的平面与此平面相交,那么该直线与______平行 a∥α,a β,α∩β=b a∥b
一条直线
交线
2.平面与平面平行的判定定理与性质定理
文字语言 图形表示 符号表示
判定定理 如果一个平面内的两条__________与另一个平面平行,那么这两个平面平行 a β,b β,a∩b=P,a∥α,b∥α α∥β
相交直线
性质 两个平面平行,则其中一个平面内的直线______于另一个平面 α∥β,a α a∥β
性质定理 两个平面平行,如果另一个平面与这两个平面______,那么两条______平行 α∥β,α∩γ=a,β∩γ=b a∥b
平行
相交
交线
1.平行关系中的三个重要结论
(1)垂直于同一条直线的两个平面平行,即若a⊥α,a⊥β,则α∥β.
(2)平行于同一平面的两个平面平行,即若α∥β,β∥γ,则α∥γ.
(3)垂直于同一个平面的两条直线平行,即若a⊥α,b⊥α,则a∥b.
2.三种平行关系的转化
(2)直线与平面垂直的判定定理与性质定理
两条相交直线
平行
练习
- - - - - - - - - -
教材152页
证明:
B
D
C
S
A
(2)两个平面垂直的判定定理与性质定理
垂线
l β
交线
l β
练习:如右图,已知PA⊥平面ABC,平面PAB⊥平面PBC.
求证:BC⊥平面PAB.
D
证明:过点A作AD⊥PB,垂足为D.
∵平面PAB⊥平面PBC, 平面PAB∩平PBC=PB,
∴AD⊥平面PBC.
∵BC 平面PBC,∴BC⊥AD.
又∵PA⊥平面ABC,BC 平面ABC,∴BC⊥PA.
又PA∩AD=A,∴BC⊥平面PAB.
P
A
B
C
2.直线和平面所成的角
(1)定义:平面的一条斜线和它在平面上的______所成的角叫做这条直线和这个平面所成的角,一条直线垂直于平面,则它们所成的角是________;一条直线和平面平行或在平面内,则它们所成的角是______.
(2)范围: .
射影
90°
0°
1. 求线面角大小的步骤:
(1) 作 — 作出平面角;
(2) 证 — 明所作的角满足定义,即为所求二面角证的平面角;
(3) 求 — 将作出的角放在三角形中,计算出平面角的大小.
简称为“一作二证三求”.
C
A
M
B
3.二面角
(1)定义:从一条直线出发的____________所组成的图形叫做二面角.
(2)二面角的平面角
若有①O∈l;②OA α,OB β;③OA⊥l,OB⊥l,则二面角α-l-β的平面角是__________.
(3)二面角的平面角α的范围:[0,π].
两个半平面
∠AOB
4. 平面与平面的夹角的定义:平面α与平面β相交所形成的4个二面角中,把其中不大于90°的二面角称为平面α与平面β的夹角.
1. 求二面角大小的步骤:
(1) 作 — 作出平面角;
(2) 证 — 明所作的角满足定义,即为所求二面角证的平面角;
(3) 求 — 将作出的角放在三角形中,计算出平面角的大小.
简称为“一作二证三求”.
2. 作出二面角的平面角的方法:
方法一:(定义法) 在二面角的棱上找一个特殊点O,在两个半平面内分别作垂直于棱的射线OA,OB.
如图所示,∠AOB为二面角α- a -β的平面角.
练习:如右图,已知PA⊥平面ABC, BC⊥AB.
求平面ABC与平面PBC所成的二面角的平面角.
D
P
A
B
C
O
A
B
1.找角:两向量同起点
2.范围:
3.求角:
4.向量夹角与数量积的关系:
5. 投影向量:
1.共线向量定理:对于任意两个空间向量 ,
①作用:判定两个向量是否共线(找λ).
②推论:判定三点是否共线(同起点&系数和为1;或转化为向量共线).
2. 共面向量定理:
作用: 判定三个向量是否共面(找x,y).
推论: 判定四点是否共面(同起点/系数和为1,或转化为三个向量共面).
1.直线的方向向量:直线的方向向量是指和这条直线平行(或在这条直线上)的有向线段所表示的向量,一条直线的方向向量有无数个.
2.平面的法向量:直线l⊥平面α,取直线l的方向向量,则这个向量叫做平面α的法向量.显然一个平面的法向量有无数个,它们是共线向量.
位置关系 向量表示 直线l1,l2的方向向量分别为n1,n2 l1∥l2 n1∥n2 n1=λn2
l1⊥l2 n1⊥n2 n1·n2=0
直线l的方向向量为n, 平面α的法向量为m l∥α n⊥m n·m=0
l⊥α n∥m n=λm
平面α,β的法向量分别为n,m α∥β n∥m n=λm
α⊥β n⊥m n·m=0
2.利用空间向量的坐标运算求夹角或距离的一般步骤
(1)建系:根据题目中的几何图形建立恰当的空间直角坐标系;
(2)求坐标:①求出相关点的坐标;②写出向量的坐标;
(3)坐标运算:结合公式进行计算、论证;
(4)翻译:将坐标运算的结果翻译为夹角或距离等集合语言.
②等面积法(将点线距离视为三角形的高)
两条平行直线m,l间的距离转化为直线m上任一点到直线l的距离
4.2求直线到直线的距离:
4.1求点到直线的距离:
4.3求点到平面的距离:
①等体积法(将点面距离看作三棱锥的高)
③找垂线法(过点找面的垂线)
平行于平面的直线到平面的距离转化为线上任意一点到平面的距离
两个平行平面间的距离转化为平面内任意一点到平面的距离
