数学人教A版(2019)必修第一册5.1.2弧度制 课件(共30张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册5.1.2弧度制 课件(共30张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 886.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-17 07:24:22 | ||
图片预览











文档简介
(共30张PPT)
5.1.2 弧度制
学习目标
1.了解弧度制,体会引入弧度制的必要性.(数学抽象)
2.能进行弧度与角度的互化,熟悉特殊角的弧度制.(数学运算)
3.掌握弧度制中扇形的弧长和面积公式,会应用公式解决简单的
问题.(数学运算)
探究新知
请思考并回答以下问题:
1.在初中学过的角度制中,1度的角是如何规定的?
2.在我们度量长度时,有时用“米”作单位,有时用“英尺”作单位,
有不同的单位制度量质量时,可以使用“千克”“磅”等不同的
单位制,角的度量除了角度制之外,是否也有其他的的单位制呢?
提示:有不同的单位制,即弧度制.
3. 在弧度制中,1弧度的角是如何规定的?如何表示?
提示: 把长度等于半径长的弧所对的圆心角叫做1弧度(radian)的角,用符号rad表示.
4. 360°的角是多少弧度的角?180°的角是多少弧度的角?1°的角呢?
5.“1弧度的角”的大小和所在圆的半径大小有关系吗?
提示: “1弧度的角”的大小是长度等于半径长的圆弧所对的圆心角,是一个定值,与所在圆的半径大小无关.
1.角度制:
(1)定义:用 作为单位来度量角的单位制.
(2)1度的角:周角的 .
2.弧度制:
(1)定义:以 作为单位来度量角的单位制.
(2)1弧度的角:长度等于 的圆弧所对的圆心角.
知 识 梳 理
知识点一 度量角的两种单位制
度
弧度
半径长
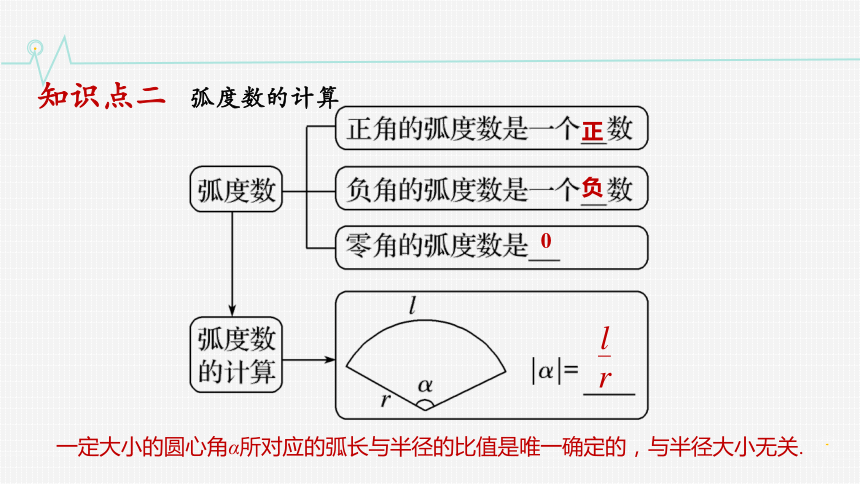
知识点二 弧度数的计算
正
负
0
一定大小的圆心角α所对应的弧长与半径的比值是唯一确定的,与半径大小无关.
知识点三 角度与弧度的互化
角度化弧度 弧度化角度
360°= rad 2π rad=_____
180°= rad π rad=_____
1°= rad≈0.017 45 rad 1 rad= ≈57.30°
角度数× =弧度数 弧度数× =角度数
2π
π
360°
180°
一些特殊角与弧度数的对应关系
0
2π
60°
180°
学习目标
知识点四 弧度制下的弧长与扇形面积公式
设扇形的半径为R,弧长为l,α(0<α<2π)为其圆心角,则
(1)弧长公式:l= .
αR
扇形的面积公式与三角形的面积公式类似.实际上,扇形可看作是
一曲边三角形,弧是底,半径是底上的高.
题 型 探 究
题型一 弧度制的概念
例1(多选题)下列说法中正确的是( )
A.弧度角与实数之间建立了一一对应的关系
C.根据弧度的定义,180°一定等于π弧度
D.无论是用角度制还是用弧度制度量角,角的大小均与圆的半径的大小有关
答案 ABC
解析 无论是用角度制还是用弧度制度量角,角的大小均与圆的半径的大小无关,而是与弧长和半径的比值有关,故D项错误.
反思感悟
对弧度制定义的三点说明
(1)不管是以弧度还是度为单位的角的大小,都是一个与半径的大小无关
的定值.
(2)在弧度制下,“弧度”二字或“rad”可以省略不写,如2 rad可简写
为2.
(3)用弧度与度去度量同一个角时,除了零角以外,所得到的数量是不同
的.
跟踪训练1 下列各说法中,错误的是
A.“度”与“弧度”是度量角的两种不同的度量单位
B.1弧度的角是长度等于半径长的弧所对的圆心角
C.根据弧度的定义,180°一定等于π弧度
D.不论用角度制还是用弧度制度量角,它们均与圆的半径长短有关
√
解析 根据角度和弧度的定义,可知无论是角度制还是弧度制,角的大小与圆的半径长短无关,而是与弧长与半径的比值有关,所以D是错误的,其他A,B,C正确.
题型二 角度制与弧度制的互化
例2
(1) ①将112°30'化为弧度为 .
反思感悟
角度制与弧度制互化的关键与方法
(1)关键:抓住互化公式π rad=180°是关键;
(2)方法:度数× =弧度数;弧度数×( )°=度数;
(3)角度化弧度时,应先将分、秒化成度,再化成弧度.
解 α<β<γ<θ=φ.
题型三 用弧度制表示角或范围
例3. 用弧度表示终边落在图中所示阴影部分内(不包括边界)的角的集合.
分析先将边界角由角度化为弧度,再根据阴影部分写出角的集合.
用弧度制表示角应注意的问题
(1)用弧度表示区域角,实质是角度表示区域角在弧度制下的应用,必要时,需
进行角度与弧度的换算.注意单位要统一,角度数与弧度数不能混用.
(2)在表示角的集合时,可以先写出一周范围(如-π~π,0~2π)内的角,再加上
2kπ,k∈Z.
(3)终边在同一直线上的角的集合可以合并为{x|x=α+kπ,k∈Z};终边在相互
垂直的两直线上的角的集合可以合并为 ,在进行区间的合并时,一定要做到准确无误.
反思感悟
跟踪训练3 以弧度为单位,写出终边落在直线y=-x上的角的集合.
题型四 扇形的弧长公式与面积公式的应用
例4
(1)已知扇形的周长为8 cm,圆心角为2,求该扇形的面积;
(2)已知扇形的周长为10 cm,面积等于4 cm2,求其圆心角的弧度数.
分析(1)先求出扇形的半径,再求面积;(2)设出圆心角,建立方程组求解.
解 (1)设扇形的半径为r cm,弧长为l cm,由圆心角为2 rad,依据弧长公式可得l=2r,从而扇形的周长为l+2r=4r=8,解得r=2,则l=4.故扇形的面积
延伸探究 本例(1)中,将条件“圆心角为2”去掉,求扇形面积的最大值.
解 设扇形的弧长为l cm,半径为r cm,则有2r+l=8,于是l=8-2r,
故当半径为2 cm,圆心角为2时,扇形面积最大值为4 cm2.
反思感悟
扇形的弧长和面积的求解策略
(1)记公式:弧度制下扇形的面积公式是S= lR= αR2(其中l是扇
形的弧长,R是扇形的半径,α是扇形圆心角的弧度数,0<α<2π).
(2)找关键:涉及扇形的半径、周长、弧长、圆心角、面积等的
计算问题,关键是分析题目中已知哪些量、求哪些量,然后灵活运用弧长公式、扇形面积公式直接求解或列方程(组)求解.
跟踪训练4 已知扇形的半径为10 cm,圆心角为60°,求扇形的弧长和面积.
小 试 牛 刀
1.下列说法中,错误的是
A.半圆所对的圆心角是π rad
B.周角的大小等于2π
C.1弧度的圆心角所对的弧长等于该圆的半径
D.长度等于半径的弦所对的圆心角的大小是1弧度
√
2.若α=-2 rad,则α的终边在
A.第一象限 B.第二象限
C.第三象限 D.第四象限
√
3.时钟的分针在1点到3点20分这段时间里转过的弧度为
√
√
5.周长为9,圆心角为1 rad的扇形面积为________.
1.知识清单:
(1)弧度制的概念.
(2)弧度与角度的相互转化.
(3)扇形的弧长与面积的计算.
2.方法归纳:消元法解方程组.
3.常见误区:弧度与角度混用.
课 后 小 结
本 课 结 束
5.1.2 弧度制
学习目标
1.了解弧度制,体会引入弧度制的必要性.(数学抽象)
2.能进行弧度与角度的互化,熟悉特殊角的弧度制.(数学运算)
3.掌握弧度制中扇形的弧长和面积公式,会应用公式解决简单的
问题.(数学运算)
探究新知
请思考并回答以下问题:
1.在初中学过的角度制中,1度的角是如何规定的?
2.在我们度量长度时,有时用“米”作单位,有时用“英尺”作单位,
有不同的单位制度量质量时,可以使用“千克”“磅”等不同的
单位制,角的度量除了角度制之外,是否也有其他的的单位制呢?
提示:有不同的单位制,即弧度制.
3. 在弧度制中,1弧度的角是如何规定的?如何表示?
提示: 把长度等于半径长的弧所对的圆心角叫做1弧度(radian)的角,用符号rad表示.
4. 360°的角是多少弧度的角?180°的角是多少弧度的角?1°的角呢?
5.“1弧度的角”的大小和所在圆的半径大小有关系吗?
提示: “1弧度的角”的大小是长度等于半径长的圆弧所对的圆心角,是一个定值,与所在圆的半径大小无关.
1.角度制:
(1)定义:用 作为单位来度量角的单位制.
(2)1度的角:周角的 .
2.弧度制:
(1)定义:以 作为单位来度量角的单位制.
(2)1弧度的角:长度等于 的圆弧所对的圆心角.
知 识 梳 理
知识点一 度量角的两种单位制
度
弧度
半径长
知识点二 弧度数的计算
正
负
0
一定大小的圆心角α所对应的弧长与半径的比值是唯一确定的,与半径大小无关.
知识点三 角度与弧度的互化
角度化弧度 弧度化角度
360°= rad 2π rad=_____
180°= rad π rad=_____
1°= rad≈0.017 45 rad 1 rad= ≈57.30°
角度数× =弧度数 弧度数× =角度数
2π
π
360°
180°
一些特殊角与弧度数的对应关系
0
2π
60°
180°
学习目标
知识点四 弧度制下的弧长与扇形面积公式
设扇形的半径为R,弧长为l,α(0<α<2π)为其圆心角,则
(1)弧长公式:l= .
αR
扇形的面积公式与三角形的面积公式类似.实际上,扇形可看作是
一曲边三角形,弧是底,半径是底上的高.
题 型 探 究
题型一 弧度制的概念
例1(多选题)下列说法中正确的是( )
A.弧度角与实数之间建立了一一对应的关系
C.根据弧度的定义,180°一定等于π弧度
D.无论是用角度制还是用弧度制度量角,角的大小均与圆的半径的大小有关
答案 ABC
解析 无论是用角度制还是用弧度制度量角,角的大小均与圆的半径的大小无关,而是与弧长和半径的比值有关,故D项错误.
反思感悟
对弧度制定义的三点说明
(1)不管是以弧度还是度为单位的角的大小,都是一个与半径的大小无关
的定值.
(2)在弧度制下,“弧度”二字或“rad”可以省略不写,如2 rad可简写
为2.
(3)用弧度与度去度量同一个角时,除了零角以外,所得到的数量是不同
的.
跟踪训练1 下列各说法中,错误的是
A.“度”与“弧度”是度量角的两种不同的度量单位
B.1弧度的角是长度等于半径长的弧所对的圆心角
C.根据弧度的定义,180°一定等于π弧度
D.不论用角度制还是用弧度制度量角,它们均与圆的半径长短有关
√
解析 根据角度和弧度的定义,可知无论是角度制还是弧度制,角的大小与圆的半径长短无关,而是与弧长与半径的比值有关,所以D是错误的,其他A,B,C正确.
题型二 角度制与弧度制的互化
例2
(1) ①将112°30'化为弧度为 .
反思感悟
角度制与弧度制互化的关键与方法
(1)关键:抓住互化公式π rad=180°是关键;
(2)方法:度数× =弧度数;弧度数×( )°=度数;
(3)角度化弧度时,应先将分、秒化成度,再化成弧度.
解 α<β<γ<θ=φ.
题型三 用弧度制表示角或范围
例3. 用弧度表示终边落在图中所示阴影部分内(不包括边界)的角的集合.
分析先将边界角由角度化为弧度,再根据阴影部分写出角的集合.
用弧度制表示角应注意的问题
(1)用弧度表示区域角,实质是角度表示区域角在弧度制下的应用,必要时,需
进行角度与弧度的换算.注意单位要统一,角度数与弧度数不能混用.
(2)在表示角的集合时,可以先写出一周范围(如-π~π,0~2π)内的角,再加上
2kπ,k∈Z.
(3)终边在同一直线上的角的集合可以合并为{x|x=α+kπ,k∈Z};终边在相互
垂直的两直线上的角的集合可以合并为 ,在进行区间的合并时,一定要做到准确无误.
反思感悟
跟踪训练3 以弧度为单位,写出终边落在直线y=-x上的角的集合.
题型四 扇形的弧长公式与面积公式的应用
例4
(1)已知扇形的周长为8 cm,圆心角为2,求该扇形的面积;
(2)已知扇形的周长为10 cm,面积等于4 cm2,求其圆心角的弧度数.
分析(1)先求出扇形的半径,再求面积;(2)设出圆心角,建立方程组求解.
解 (1)设扇形的半径为r cm,弧长为l cm,由圆心角为2 rad,依据弧长公式可得l=2r,从而扇形的周长为l+2r=4r=8,解得r=2,则l=4.故扇形的面积
延伸探究 本例(1)中,将条件“圆心角为2”去掉,求扇形面积的最大值.
解 设扇形的弧长为l cm,半径为r cm,则有2r+l=8,于是l=8-2r,
故当半径为2 cm,圆心角为2时,扇形面积最大值为4 cm2.
反思感悟
扇形的弧长和面积的求解策略
(1)记公式:弧度制下扇形的面积公式是S= lR= αR2(其中l是扇
形的弧长,R是扇形的半径,α是扇形圆心角的弧度数,0<α<2π).
(2)找关键:涉及扇形的半径、周长、弧长、圆心角、面积等的
计算问题,关键是分析题目中已知哪些量、求哪些量,然后灵活运用弧长公式、扇形面积公式直接求解或列方程(组)求解.
跟踪训练4 已知扇形的半径为10 cm,圆心角为60°,求扇形的弧长和面积.
小 试 牛 刀
1.下列说法中,错误的是
A.半圆所对的圆心角是π rad
B.周角的大小等于2π
C.1弧度的圆心角所对的弧长等于该圆的半径
D.长度等于半径的弦所对的圆心角的大小是1弧度
√
2.若α=-2 rad,则α的终边在
A.第一象限 B.第二象限
C.第三象限 D.第四象限
√
3.时钟的分针在1点到3点20分这段时间里转过的弧度为
√
√
5.周长为9,圆心角为1 rad的扇形面积为________.
1.知识清单:
(1)弧度制的概念.
(2)弧度与角度的相互转化.
(3)扇形的弧长与面积的计算.
2.方法归纳:消元法解方程组.
3.常见误区:弧度与角度混用.
课 后 小 结
本 课 结 束
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
