初中数学(鲁教版)七年级下册7.4二元一次方程与一次函数课件 54张PPT
文档属性
| 名称 | 初中数学(鲁教版)七年级下册7.4二元一次方程与一次函数课件 54张PPT |
|
|
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-18 00:00:00 | ||
图片预览










文档简介
(共54张PPT)
4 二元一次方程与一次函数
1.理解二元一次方程和一次函数的关系;掌握二元一次方程组和对应的两条直线之间的关系;掌握二元一次方程组的图象解法.
2.理解作函数图象的方法与代数方法各自的特点.掌握利用二元一次方程组确定一次函数的表达式.进一步理解方程与函数的联系.
一次函数
这是怎么回事?
二元一次方程
你知道y=x+1是什么吗?
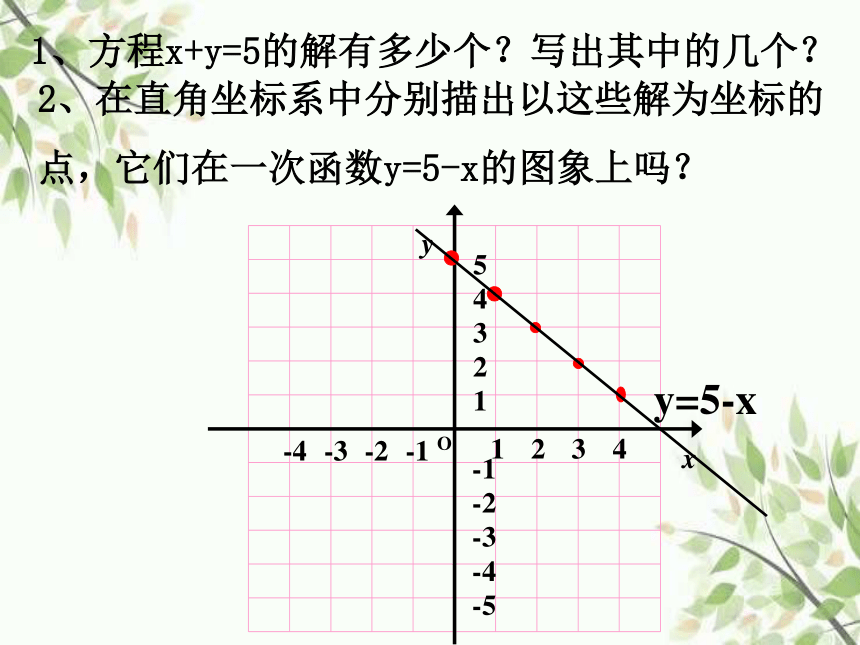
1、方程x+y=5的解有多少个?写出其中的几个?
2、在直角坐标系中分别描出以这些解为坐标的点,它们在一次函数y=5-x的图象上吗?
O
4
3
1
2
y
x
2
3
4
5
1
-1
-2
-4
-3
-4
-3
-2
-1
-5
y=5-x
3、在一次函数y=5-x的图象上任取一点,它的坐标适合方程x+y=5吗?
O
4
3
1
2
y
x
2
3
4
5
1
-1
-2
-4
-3
-4
-3
-2
-1
-5
y=5-x
4、以方程x+y=5的解为坐标的所有点组成的图象与一次函数y=5-x的图象相同吗?
知识源于悟:
通过以上结论,你能分析研究出二元一次方程和一次函数图象的关系吗?
一般地,以一个二元一次方程的解为坐标的点组成的图象与相应的一次函数的图象相同,是一条直线
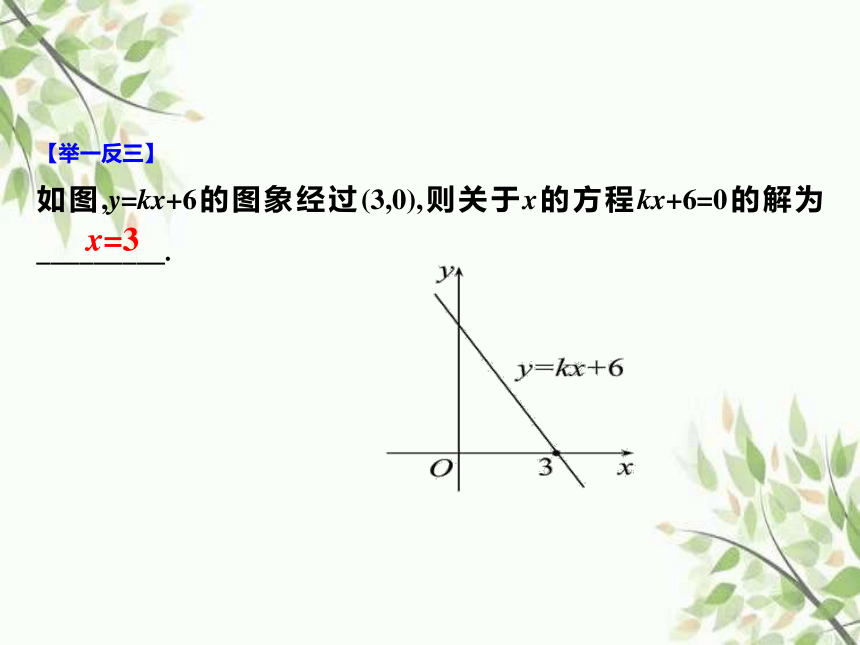
【举一反三】
如图,y=kx+6的图象经过(3,0),则关于x的方程kx+6=0的解为_________.
x=3
(梧州·中考)直线y=2x+b与x轴的交点坐标是
(2,0),则关于x的方程2x+b=0的解是x=______
【小题快练】
1.在平面直角坐标系中,二元一次方程ax+by=c的图象如图所示,则当x=4时,y的值
为_______.
-1
【例1】用作图象的方法解方程组:
(1)书写步骤;
A 二元一次方程化为一次函数
B 作函数图象
C 找交点
D 方程组的解
(2)书写格式.
注 意
【例题】
取点(-2,0),(0,1)作出直线 .
由②得:
x
3
2
1
-1
-2
y
-2
2
-1
0
1
3
【解析】由①得:
取点(1,0),(0,-2),作出直线
观察图象得出交点为P(2,2).
P
如图,直线
的交点坐标是____.
x
y
-2
2
-1
0
1
3
3
2
1
-1
-2
【跟踪训练】
3
2
1
-1
-2
x
y
-2
2
-1
0
1
3
答案:
二元一次方程组有哪些解法?
消元法
二元一次方程组与一次函数有何联系?
二元一次方程组的解是它们对应的两个一次函数图象的交点坐标;反之,两个一次函数图象的交点也是它们所对应的二元一次方程组的解.
正因如此,方程问题可以通过函数知识来解决,反之,函数问题也可以通过方程知识来解决.
图象法
是一种代数方法
【规律方法】
2.方程组的解即为直线y=-x+b与直线y=2x的______________.
交点坐标
3.已知直线y=2x+1与y=-x+b的交点为(-1,a),则方程组的解为_______.
____
【举一反三】
1. (2023·泰安新泰市期末)如图,已知一次函数y=x+1和一次函数y=ax+3图象交于点P,点P的横坐标为1,那么方程y=x+1和方程y=ax+3的公共解为( )
A. B.
C. D.
B
如图,两条直线
的交点坐标可以看作哪个方程组的解?
答案:
3
-1
2
-3
x
y
0
(镇江·中考)两直线
的交点坐标为( )
A.(—2,3) B.(2,—3)
C.(—2,—3) D.(2,3)
D
1
-9
【举一反三】
如图,已知B中的实数与A中的实数之间的对应关系是某个一次函数.若用y表示B
中的实数,用x表示A中的实数,则a=_______.
1
6.如图中的两直线l1,l2 的交点坐标可以看作方程组
____________的解
1
2
3
4
x
2
3
4
1
-1
y
0
-1
l1
l2
1
2.如图,直线l1,l2的交点A坐标可以看作方程组 _______________的解.
想一想
在同一直角坐标系内,一次函数y=x+1和y=x-2的图象有怎样的位置关系?方程组
x-y=-1的解的情况如何?你发现了什么?
x-y=2
O
4
3
1
2
y
x
2
3
4
5
1
-1
-2
-4
-3
-4
-3
-2
-1
-5
y=x+1
y=x-2
【小题快练】
1.若方程组没有解,则一次函数y=2-x与y=-x的图象必定( )
A.重合 B.平行
C.相交 D.无法确定
B
4.如果一次函数y=x+1与一次函数y=kx+b平行,则关于x,y的方程组的解的情
况是__________.
无解
重点·典例研析
【重点1】二元一次方程与一次函数的关系
【典例1】一个二元一次方程ax+by=c(a,b,c为常数,且a,b均不为0)有无数组解,我们规定,将其每一个解中x,y的值分别作为一个点的横,纵坐标,交点在平面直角坐标系中,这样我们就得到了二元一次方程的图象:一条直线,即二元一次方程的解均满足其对应直线上点的坐标,反之直线上点的坐标均为其对应的二元一次方程的解,如2x-y=0,其中一解x=1,y=2,则对应其图象上一个点(1,2).
(1)如图,3x+3y=12的图象为直线m,与x轴的交点A的坐标为_______,与y轴的交点B的坐标为_______.
(2)如图,ax+by=-5的图象为直线n,其与x轴交于C(-,0),与(1)中直线m交于
点P,若点P的横坐标为1,求a和b的值.
[解](1)令3x+3y=12中y=0,
则3x=12,解得:x=4,
所以A(4,0);
令3x+3y=12中x=0,
则3y=12,解得:y=4,
所以B(0,4).
答案:(4,0) (0,4)
(2)令3x+3y=12中x=1,则3+3y=12,
解得:y=3,所以P(1,3).
将C,P(1,3)代入ax+by=-5中,
得:解得
【重点2】二元一次方程组与一次函数的关系
【典例2】(2023·烟台芝罘区期中)若正比例函数y=-2x的图象与一次函数y=x+m的图象交于点A,且点A的横坐标为-3.
(1)求该一次函数的表达式.
(2)直接写出方程组的解.
[自主解答](1)将x=-3代入y=-2x,得y=6,
则点A坐标为(-3,6).
将A(-3,6)代入y=x+m,得-3+m=6,
解得m=9,
所以一次函数的表达式为y=x+9;
(2)方程组的解为.
一次函数与面积
7.求两条直线y=3x-2与
y=-2x+4和x轴所围成的三角形的面积.
答案:
-2
-1
4
3
2
1
2
1
x
y
O
2.(2023·泰安岱岳区质检)如图所示,直线l1的函数表达式为y=3x-2,且直线l1与x轴交于点D.直线l2与x轴交于点A,且经过点B(4,1),直线l1与l2交于点C(m,3).
(1)求点D和点C的坐标;
(2)已知l2的函数表达式为y=-x+,利用函数图象写出关于x,y的二元一次方程组的解;
(3)求两直线与x轴围成的三角形面积.
【解析】(1)在y=3x-2中,
令y=0,即3x-2=0,
解得x=,所以D(,0),
因为点C(m,3)在直线y=3x-2上,
所以3m-2=3,所以m=,所以C(,3);
(2)由题图可知,二元一次方程组的解为.
(3)易知A(,0),所以AD=-=,
所以S△ADC=×3×0.5=.
重点·典例研析
【重点1】二元一次方程组与待定系数法
【典例1】(2023·淄博张店区期末)如图,直线l1:y1=kx+b与y轴交于点A,与x轴交于点B(,0),直线l2:y2=-x+2与y轴交于点C,与直线l1交于点D,点D到y轴的距离为2.
(1)求直线l1的函数表达式;
(2)请直接写出方程组的解: _____________________;
(3)求△ACD的面积;
(4)在直线l1上是否存在异于点D的另一点M,使得△ACD与△ACM的
面积相等 若存在,请求出点M的坐标;若不存在,请说明理由.
【自主解答】(1)因为点D到y轴的距离为2,
所以点D的横坐标为2,
把x=2代入y2=-x+2得,y2=-×2+2=1,
所以D(2,1),
把B(,0),D(2,1)代入y1=kx+b,得,所以.
所以直线l1的函数表达式为y1=2x-3;
(2)因为直线l1:y1=kx+b与直线l2:y2=-x+2交于点D(2,1),
所以方程组的解是.
答案:
(3)把x=0代入y2=-x+2,得y2=2,
所以C(0,2),把x=0代入y1=2x-3,得y1=-3.
所以A(0,-3).
所以AC=2+3=5.所以S△ACD=×5×2=5;
(4)存在,
因为在直线l1上存在异于点D的另一点M,使得△ACD与△ACM的面积相等,
所以M点到y轴的距离为2,
因为点D的横坐标为2,
所以点M的横坐标为-2,
把x=-2代入y1=2x-3得,y1=2×(-2)-3=-7,
所以M点的坐标为(-2,-7).
一次函数实际应用
A,B 两地相距100 km,甲、乙两人骑自行车分别从A,B两地相向而行.假设他们都保持匀速行驶,则他们各自到A地的距离s(km)都是骑车时间t (h)的一次函数.1 h后乙距A地80 km; 2小时后甲距A地30 km.
问:经过多长时间两人相遇
直线型图表示
80 km
乙
1时
议一议
2时,30 km
甲
B
A
你明白他的想法吗?
用他的方法做一做!
图象表示
(A)
0
4
1
2
3
t/h
s/km
120
100
80
60
40
20
(B)
【解析】可以分别作出两人
s 与t 之间的关系
图象,找出交点
的横坐标就行了!
小明
5
【解析】1 小时后乙距A地80 km,即乙的速度是
20 km/h, 2 小时后甲距A 地 30 km,
故甲的速度是 15 km/h,由此可求出
甲、乙两人的速度和 ……
小彬
你明白他的想法吗?
用他的方法做一做!
t=
小颖
【解析】对于乙,s 是t的一次函数,可设 s=kt+b.
当t=0时,s=100;
当t=1时,s=80.将它们分别代入s=kt+b中,可以求出k,b的值,也即可以求出乙s与t 之间的函数表达式.
同样可求出甲s与t之间的函数表达式.
再联立这两个表达式,求解方程组就行了.
你明白她的想法吗?用她的方法做一做!
消去 s
小明
小彬
小颖
用作图象的方法可以直观地获得问题的结果,但有时却难以保证准确,为了获得准确的结果,我们一般用代数方法.
在以上的解题过程中你受到什么启发?
用一元一次方程的方法可以解决问题
用图象法可以解决问题
用方程组的方法可以解决问题
【例2】某长途汽车客运站规定,乘客可以免费携带一定质量的行李,但超过该质量则需购买行李票,且行李费y(元)是行李质量x(kg)的一次函数.已知李明带了60 kg的行李,交了行李费5元;张华带了90 kg的行李,交了行李费10元.
(1)写出y与x之间的函数表达式;
(2)旅客最多可免费携带多少千克的行李?
【例题】
【解析】(1)设此一次函数表达式为:y=kx+b(k≠0) . 根据题意,可得方程组
解得
(2)当x=30时,y=0.
所以旅客最多可免费携带30 kg的行李.
某市自来水公司为鼓励居民节约用水,采取按月用
水量分段收费办法,若某户居民应交水费y(元)与用水量x(t)的函数关系如图所示.
O
y(元)
x(t)
15
20
27
39
【跟踪训练】
(2)若某用户十月份用水量为10 t,则应交水费多少元?若该用户十一月份交了51元的水费,则他该月用水多少吨?
(1)分别写出当0≤x≤15和x>15时,y与x的函数关系式;
【解析】(1)当0≤x≤15时,设y=kx,根据题意,可得方程27=15k,解得
. ①
当x>15时,设y=mx+n,根据题意,可得方程组
解得
. ②
(2)当x=10 时(10<15),
代入①中可得y=18;
当y=51 时(51>27),
代入②中可得x=25.
3.甲超市进行苹果优惠促销活动,苹果的标价为10元/kg,如果一次购买4 kg以上的苹果,超过4 kg的部分按标价的6折售卖.
x(单位:kg)表示购买苹果的重量,y(单位:元)表示付款金额.
(1)文文购买3 kg苹果需付款________元;
购买5 kg苹果需付款________元.
(2)写出付款金额y关于购买苹果的重量x的函数表达式:
当0当x>4时,_____________.
30
46
y=10x
y=6x+16
【重点2】二元一次方程组与一次函数的应用
【典例2】在一条笔直的公路旁依次有A,B,C三个村庄,甲、乙两人同时分别从A,B两村
出发,甲骑摩托车,乙骑电动车沿公路匀速驶向C村,最终到达C村.设甲、乙两人到C村
的距离y1,y2(km)与行驶时间x(h)之间的函数关系如图所示,若乙在行驶过程中与甲相距
5 km,则x的值为____________.
或或
【举一反三】
1.同学们,还记得“龟兔赛跑”的故事吗 兔子在第一次龟兔赛跑中失败了很不服气,于是
找到乌龟再比一次,鉴于兔子跑得明显快于乌龟,于是兔子让乌龟先跑一段时间,本次比
赛兔子破了自己的记录达到了米/秒,如图是两者所跑的路程s与时间t的关系,下列说
法正确的是( )
A.两者同时到达终点
B.乌龟先跑了40分钟
C.两者在第分钟时相遇
D.兔子的速度是乌龟的9倍
C
2.如图是某地出租车的乘车里程和所付车费之间的关系图象,分别有线段AB,BC和射线
CD组成.张老师乘坐出租车里程是8千米.他应该付车费________元.
20
4 二元一次方程与一次函数
1.理解二元一次方程和一次函数的关系;掌握二元一次方程组和对应的两条直线之间的关系;掌握二元一次方程组的图象解法.
2.理解作函数图象的方法与代数方法各自的特点.掌握利用二元一次方程组确定一次函数的表达式.进一步理解方程与函数的联系.
一次函数
这是怎么回事?
二元一次方程
你知道y=x+1是什么吗?
1、方程x+y=5的解有多少个?写出其中的几个?
2、在直角坐标系中分别描出以这些解为坐标的点,它们在一次函数y=5-x的图象上吗?
O
4
3
1
2
y
x
2
3
4
5
1
-1
-2
-4
-3
-4
-3
-2
-1
-5
y=5-x
3、在一次函数y=5-x的图象上任取一点,它的坐标适合方程x+y=5吗?
O
4
3
1
2
y
x
2
3
4
5
1
-1
-2
-4
-3
-4
-3
-2
-1
-5
y=5-x
4、以方程x+y=5的解为坐标的所有点组成的图象与一次函数y=5-x的图象相同吗?
知识源于悟:
通过以上结论,你能分析研究出二元一次方程和一次函数图象的关系吗?
一般地,以一个二元一次方程的解为坐标的点组成的图象与相应的一次函数的图象相同,是一条直线
【举一反三】
如图,y=kx+6的图象经过(3,0),则关于x的方程kx+6=0的解为_________.
x=3
(梧州·中考)直线y=2x+b与x轴的交点坐标是
(2,0),则关于x的方程2x+b=0的解是x=______
【小题快练】
1.在平面直角坐标系中,二元一次方程ax+by=c的图象如图所示,则当x=4时,y的值
为_______.
-1
【例1】用作图象的方法解方程组:
(1)书写步骤;
A 二元一次方程化为一次函数
B 作函数图象
C 找交点
D 方程组的解
(2)书写格式.
注 意
【例题】
取点(-2,0),(0,1)作出直线 .
由②得:
x
3
2
1
-1
-2
y
-2
2
-1
0
1
3
【解析】由①得:
取点(1,0),(0,-2),作出直线
观察图象得出交点为P(2,2).
P
如图,直线
的交点坐标是____.
x
y
-2
2
-1
0
1
3
3
2
1
-1
-2
【跟踪训练】
3
2
1
-1
-2
x
y
-2
2
-1
0
1
3
答案:
二元一次方程组有哪些解法?
消元法
二元一次方程组与一次函数有何联系?
二元一次方程组的解是它们对应的两个一次函数图象的交点坐标;反之,两个一次函数图象的交点也是它们所对应的二元一次方程组的解.
正因如此,方程问题可以通过函数知识来解决,反之,函数问题也可以通过方程知识来解决.
图象法
是一种代数方法
【规律方法】
2.方程组的解即为直线y=-x+b与直线y=2x的______________.
交点坐标
3.已知直线y=2x+1与y=-x+b的交点为(-1,a),则方程组的解为_______.
____
【举一反三】
1. (2023·泰安新泰市期末)如图,已知一次函数y=x+1和一次函数y=ax+3图象交于点P,点P的横坐标为1,那么方程y=x+1和方程y=ax+3的公共解为( )
A. B.
C. D.
B
如图,两条直线
的交点坐标可以看作哪个方程组的解?
答案:
3
-1
2
-3
x
y
0
(镇江·中考)两直线
的交点坐标为( )
A.(—2,3) B.(2,—3)
C.(—2,—3) D.(2,3)
D
1
-9
【举一反三】
如图,已知B中的实数与A中的实数之间的对应关系是某个一次函数.若用y表示B
中的实数,用x表示A中的实数,则a=_______.
1
6.如图中的两直线l1,l2 的交点坐标可以看作方程组
____________的解
1
2
3
4
x
2
3
4
1
-1
y
0
-1
l1
l2
1
2.如图,直线l1,l2的交点A坐标可以看作方程组 _______________的解.
想一想
在同一直角坐标系内,一次函数y=x+1和y=x-2的图象有怎样的位置关系?方程组
x-y=-1的解的情况如何?你发现了什么?
x-y=2
O
4
3
1
2
y
x
2
3
4
5
1
-1
-2
-4
-3
-4
-3
-2
-1
-5
y=x+1
y=x-2
【小题快练】
1.若方程组没有解,则一次函数y=2-x与y=-x的图象必定( )
A.重合 B.平行
C.相交 D.无法确定
B
4.如果一次函数y=x+1与一次函数y=kx+b平行,则关于x,y的方程组的解的情
况是__________.
无解
重点·典例研析
【重点1】二元一次方程与一次函数的关系
【典例1】一个二元一次方程ax+by=c(a,b,c为常数,且a,b均不为0)有无数组解,我们规定,将其每一个解中x,y的值分别作为一个点的横,纵坐标,交点在平面直角坐标系中,这样我们就得到了二元一次方程的图象:一条直线,即二元一次方程的解均满足其对应直线上点的坐标,反之直线上点的坐标均为其对应的二元一次方程的解,如2x-y=0,其中一解x=1,y=2,则对应其图象上一个点(1,2).
(1)如图,3x+3y=12的图象为直线m,与x轴的交点A的坐标为_______,与y轴的交点B的坐标为_______.
(2)如图,ax+by=-5的图象为直线n,其与x轴交于C(-,0),与(1)中直线m交于
点P,若点P的横坐标为1,求a和b的值.
[解](1)令3x+3y=12中y=0,
则3x=12,解得:x=4,
所以A(4,0);
令3x+3y=12中x=0,
则3y=12,解得:y=4,
所以B(0,4).
答案:(4,0) (0,4)
(2)令3x+3y=12中x=1,则3+3y=12,
解得:y=3,所以P(1,3).
将C,P(1,3)代入ax+by=-5中,
得:解得
【重点2】二元一次方程组与一次函数的关系
【典例2】(2023·烟台芝罘区期中)若正比例函数y=-2x的图象与一次函数y=x+m的图象交于点A,且点A的横坐标为-3.
(1)求该一次函数的表达式.
(2)直接写出方程组的解.
[自主解答](1)将x=-3代入y=-2x,得y=6,
则点A坐标为(-3,6).
将A(-3,6)代入y=x+m,得-3+m=6,
解得m=9,
所以一次函数的表达式为y=x+9;
(2)方程组的解为.
一次函数与面积
7.求两条直线y=3x-2与
y=-2x+4和x轴所围成的三角形的面积.
答案:
-2
-1
4
3
2
1
2
1
x
y
O
2.(2023·泰安岱岳区质检)如图所示,直线l1的函数表达式为y=3x-2,且直线l1与x轴交于点D.直线l2与x轴交于点A,且经过点B(4,1),直线l1与l2交于点C(m,3).
(1)求点D和点C的坐标;
(2)已知l2的函数表达式为y=-x+,利用函数图象写出关于x,y的二元一次方程组的解;
(3)求两直线与x轴围成的三角形面积.
【解析】(1)在y=3x-2中,
令y=0,即3x-2=0,
解得x=,所以D(,0),
因为点C(m,3)在直线y=3x-2上,
所以3m-2=3,所以m=,所以C(,3);
(2)由题图可知,二元一次方程组的解为.
(3)易知A(,0),所以AD=-=,
所以S△ADC=×3×0.5=.
重点·典例研析
【重点1】二元一次方程组与待定系数法
【典例1】(2023·淄博张店区期末)如图,直线l1:y1=kx+b与y轴交于点A,与x轴交于点B(,0),直线l2:y2=-x+2与y轴交于点C,与直线l1交于点D,点D到y轴的距离为2.
(1)求直线l1的函数表达式;
(2)请直接写出方程组的解: _____________________;
(3)求△ACD的面积;
(4)在直线l1上是否存在异于点D的另一点M,使得△ACD与△ACM的
面积相等 若存在,请求出点M的坐标;若不存在,请说明理由.
【自主解答】(1)因为点D到y轴的距离为2,
所以点D的横坐标为2,
把x=2代入y2=-x+2得,y2=-×2+2=1,
所以D(2,1),
把B(,0),D(2,1)代入y1=kx+b,得,所以.
所以直线l1的函数表达式为y1=2x-3;
(2)因为直线l1:y1=kx+b与直线l2:y2=-x+2交于点D(2,1),
所以方程组的解是.
答案:
(3)把x=0代入y2=-x+2,得y2=2,
所以C(0,2),把x=0代入y1=2x-3,得y1=-3.
所以A(0,-3).
所以AC=2+3=5.所以S△ACD=×5×2=5;
(4)存在,
因为在直线l1上存在异于点D的另一点M,使得△ACD与△ACM的面积相等,
所以M点到y轴的距离为2,
因为点D的横坐标为2,
所以点M的横坐标为-2,
把x=-2代入y1=2x-3得,y1=2×(-2)-3=-7,
所以M点的坐标为(-2,-7).
一次函数实际应用
A,B 两地相距100 km,甲、乙两人骑自行车分别从A,B两地相向而行.假设他们都保持匀速行驶,则他们各自到A地的距离s(km)都是骑车时间t (h)的一次函数.1 h后乙距A地80 km; 2小时后甲距A地30 km.
问:经过多长时间两人相遇
直线型图表示
80 km
乙
1时
议一议
2时,30 km
甲
B
A
你明白他的想法吗?
用他的方法做一做!
图象表示
(A)
0
4
1
2
3
t/h
s/km
120
100
80
60
40
20
(B)
【解析】可以分别作出两人
s 与t 之间的关系
图象,找出交点
的横坐标就行了!
小明
5
【解析】1 小时后乙距A地80 km,即乙的速度是
20 km/h, 2 小时后甲距A 地 30 km,
故甲的速度是 15 km/h,由此可求出
甲、乙两人的速度和 ……
小彬
你明白他的想法吗?
用他的方法做一做!
t=
小颖
【解析】对于乙,s 是t的一次函数,可设 s=kt+b.
当t=0时,s=100;
当t=1时,s=80.将它们分别代入s=kt+b中,可以求出k,b的值,也即可以求出乙s与t 之间的函数表达式.
同样可求出甲s与t之间的函数表达式.
再联立这两个表达式,求解方程组就行了.
你明白她的想法吗?用她的方法做一做!
消去 s
小明
小彬
小颖
用作图象的方法可以直观地获得问题的结果,但有时却难以保证准确,为了获得准确的结果,我们一般用代数方法.
在以上的解题过程中你受到什么启发?
用一元一次方程的方法可以解决问题
用图象法可以解决问题
用方程组的方法可以解决问题
【例2】某长途汽车客运站规定,乘客可以免费携带一定质量的行李,但超过该质量则需购买行李票,且行李费y(元)是行李质量x(kg)的一次函数.已知李明带了60 kg的行李,交了行李费5元;张华带了90 kg的行李,交了行李费10元.
(1)写出y与x之间的函数表达式;
(2)旅客最多可免费携带多少千克的行李?
【例题】
【解析】(1)设此一次函数表达式为:y=kx+b(k≠0) . 根据题意,可得方程组
解得
(2)当x=30时,y=0.
所以旅客最多可免费携带30 kg的行李.
某市自来水公司为鼓励居民节约用水,采取按月用
水量分段收费办法,若某户居民应交水费y(元)与用水量x(t)的函数关系如图所示.
O
y(元)
x(t)
15
20
27
39
【跟踪训练】
(2)若某用户十月份用水量为10 t,则应交水费多少元?若该用户十一月份交了51元的水费,则他该月用水多少吨?
(1)分别写出当0≤x≤15和x>15时,y与x的函数关系式;
【解析】(1)当0≤x≤15时,设y=kx,根据题意,可得方程27=15k,解得
. ①
当x>15时,设y=mx+n,根据题意,可得方程组
解得
. ②
(2)当x=10 时(10<15),
代入①中可得y=18;
当y=51 时(51>27),
代入②中可得x=25.
3.甲超市进行苹果优惠促销活动,苹果的标价为10元/kg,如果一次购买4 kg以上的苹果,超过4 kg的部分按标价的6折售卖.
x(单位:kg)表示购买苹果的重量,y(单位:元)表示付款金额.
(1)文文购买3 kg苹果需付款________元;
购买5 kg苹果需付款________元.
(2)写出付款金额y关于购买苹果的重量x的函数表达式:
当0
30
46
y=10x
y=6x+16
【重点2】二元一次方程组与一次函数的应用
【典例2】在一条笔直的公路旁依次有A,B,C三个村庄,甲、乙两人同时分别从A,B两村
出发,甲骑摩托车,乙骑电动车沿公路匀速驶向C村,最终到达C村.设甲、乙两人到C村
的距离y1,y2(km)与行驶时间x(h)之间的函数关系如图所示,若乙在行驶过程中与甲相距
5 km,则x的值为____________.
或或
【举一反三】
1.同学们,还记得“龟兔赛跑”的故事吗 兔子在第一次龟兔赛跑中失败了很不服气,于是
找到乌龟再比一次,鉴于兔子跑得明显快于乌龟,于是兔子让乌龟先跑一段时间,本次比
赛兔子破了自己的记录达到了米/秒,如图是两者所跑的路程s与时间t的关系,下列说
法正确的是( )
A.两者同时到达终点
B.乌龟先跑了40分钟
C.两者在第分钟时相遇
D.兔子的速度是乌龟的9倍
C
2.如图是某地出租车的乘车里程和所付车费之间的关系图象,分别有线段AB,BC和射线
CD组成.张老师乘坐出租车里程是8千米.他应该付车费________元.
20
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
