第二单元练习卷(单元测试)小学数学五年级下册 北师大版(基础篇)(含答案)
文档属性
| 名称 | 第二单元练习卷(单元测试)小学数学五年级下册 北师大版(基础篇)(含答案) |  | |
| 格式 | Doc | ||
| 文件大小 | 241.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-17 20:33:56 | ||
图片预览




文档简介
(基础篇)2023-2024学年下学期小学数学北师大新版五年级第二单元练习卷
一.选择题(共7小题)
1.长方体(不含正方体)的六个面中,最多有( )个面的面积相等。
A.6 B.4 C.3 D.2
2.加工一套空调外机的包装箱要用多少材料,是求包装箱的( )
A.表面积 B.体积 C.容积 D.棱长总和
3.用一根长1m的铁丝,正好能焊接成长10cm,宽5cm,高( )cm的长方体。
A.40 B.8 C.10 D.15
4.如图:将如图的纸片折起来可以做成一个正方体.这个正方体的6号面的对面是( )号面.
A.2 B.3 C.4
5.将展开图围成正方体后,标有“冬”字的那面就会与标有“( )”字的面相对。
A.春 B.夏 C.秋 D.季
6.从一个体积是30m3的长方体木块中挖掉一小块后(如图),它的表面积( )
A.比原来大 B.比原来小
C.和原来一样大 D.无法确定
7.笑笑把4盒长12cm,宽和高都是5cm的长方体礼品包装在一起,下面4种方法中,最节省包装纸的是( )
A.
B.
C.
D.
二.填空题(共5小题)
8.如图所示的平面图形折叠成一个正方体,“会”字对面的字是 。
9.长方体中,相交于一个顶点的三条棱的长度分别是7分米,5分米,4分米,要用铁丝围一个这样的长方体框架,需要铁丝 分米。(接头处忽略不计)
10.用一根长36cm的铁丝做一个宽是2cm,高是3cm的长方体框架,这个框架的长是 cm,如做成一个正方体,正方体一个面的面积是 cm2
11.把一个表面积是100平方分米的长方体,参照右图切三次,切后的表面积之和比原来增加了 平方分米。
12.把一个长是6dm的长方体按右面三种方法分割成两个相同的小长方体,两个小长方体的表面积之和分别比原来长方体的表面积增加了48dm2、36dm2、24dm2,原来长方体的宽是 dm,高是 dm。
三.判断题(共4小题)
13.正方体是长、宽、高都相等的长方体。
14.有6个面,8个顶点,12条棱的物体都是长方体. .
15.在同一位置看一个长方体,最多只能看到它的三个面. .
16.一个正方体的棱长总和是72dm,它的表面积是216dm2。
四.计算题(共2小题)
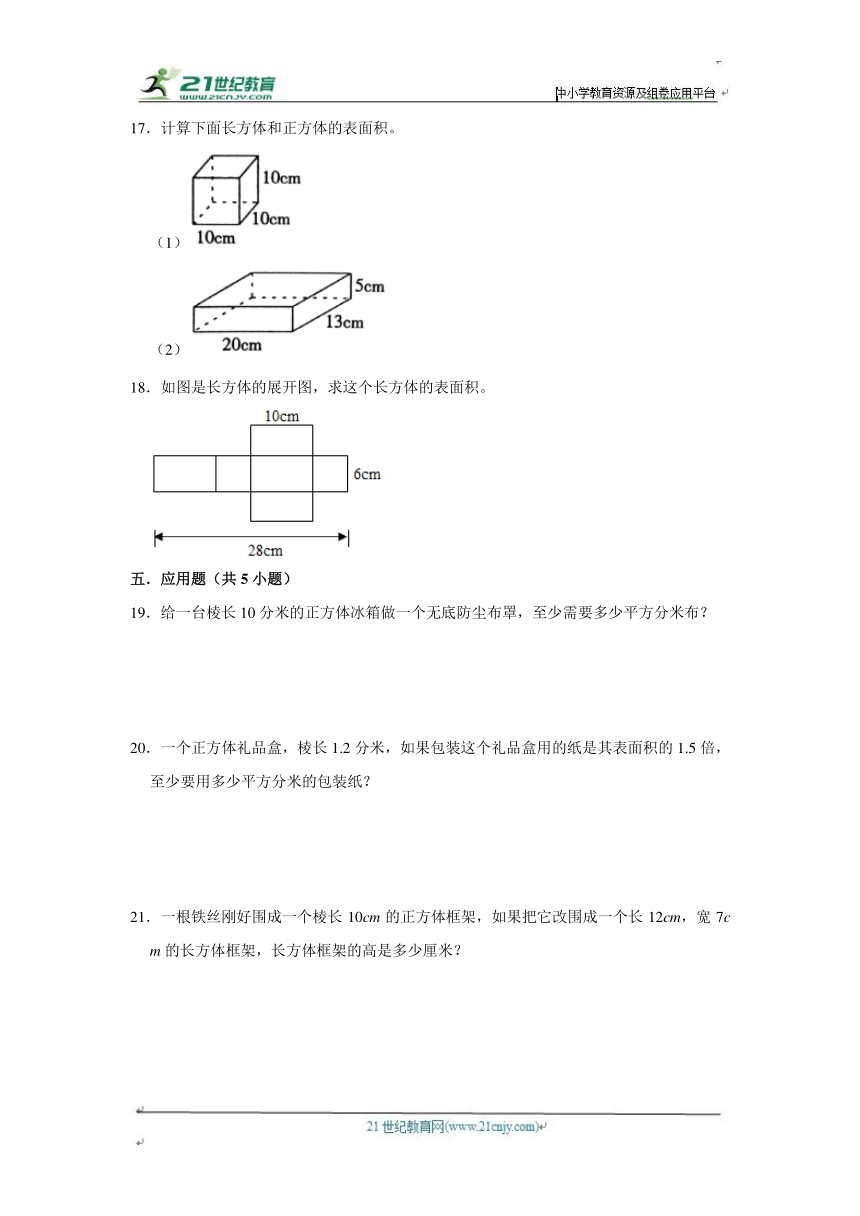
17.计算下面长方体和正方体的表面积。
(1)
(2)
18.如图是长方体的展开图,求这个长方体的表面积。
五.应用题(共5小题)
19.给一台棱长10分米的正方体冰箱做一个无底防尘布罩,至少需要多少平方分米布?
20.一个正方体礼品盒,棱长1.2分米,如果包装这个礼品盒用的纸是其表面积的1.5倍,至少要用多少平方分米的包装纸?
21.一根铁丝刚好围成一个棱长10cm的正方体框架,如果把它改围成一个长12cm,宽7cm的长方体框架,长方体框架的高是多少厘米?
22.某小学要粉刷新教室,除地板与门窗外,其余都要粉刷。已知教室的长是8m,宽6m,高4m,门窗的面积是12.5m2。如果每平方米需要花4元涂料费,粉刷这个教室需要花费多少钱?
23.一个小长方体长3cm,宽2cm,高1cm,把三个这样的小长方体拼成一个大长方体,在大长方体的表面刷一层油漆,刷油漆的面积最少是多少?
长/cm 宽/cm 高/cm 表面积/cm2
(基础篇)2023-2024学年下学期小学数学北师大新版五年级第二单元练习卷
参考答案与试题解析
一.选择题(共7小题)
1.长方体(不含正方体)的六个面中,最多有( )个面的面积相等。
A.6 B.4 C.3 D.2
【解答】解:在长方体中如果有两个相对的面是正方形,那么它的4个侧面是完全相同的长方形;
因此,长方体(不包括正方体)的六个面中,最多有4个的面积相等。
故选:B。
2.加工一套空调外机的包装箱要用多少材料,是求包装箱的( )
A.表面积 B.体积 C.容积 D.棱长总和
【解答】解:根据题干可得,
加工一套空调外机的包装箱要用多少材料,是求包装箱的表面积。
故选:A。
3.用一根长1m的铁丝,正好能焊接成长10cm,宽5cm,高( )cm的长方体。
A.40 B.8 C.10 D.15
【解答】解:1m=100cm
100÷4﹣(10+5)
=25﹣15
=10(厘米)
答:用一根长1m的铁丝,正好能焊接成长10cm,宽5cm,高10厘米的长方体。
故选:C。
4.如图:将如图的纸片折起来可以做成一个正方体.这个正方体的6号面的对面是( )号面.
A.2 B.3 C.4
【解答】解:纸片折起来可以做成一个正方体后:3号面对2号面,1号面对5号面,4号面对6号面.
故选:C。
5.将展开图围成正方体后,标有“冬”字的那面就会与标有“( )”字的面相对。
A.春 B.夏 C.秋 D.季
【解答】解:将展开图围成正方体后,标有“冬”字的那面就会与标有“春”字的面相对。
故选:A。
6.从一个体积是30m3的长方体木块中挖掉一小块后(如图),它的表面积( )
A.比原来大 B.比原来小
C.和原来一样大 D.无法确定
【解答】解:从一个体积是30m3的长方体木块中挖掉一小块后,它的表面积比原来大。
故选:A。
7.笑笑把4盒长12cm,宽和高都是5cm的长方体礼品包装在一起,下面4种方法中,最节省包装纸的是( )
A.
B.
C.
D.
【解答】解:A、12×5×8
=60×8
=480(平方厘米)
B、12×5×4+5×5×4
=240+100
=340(平方厘米)
C、5×5×6
=25×6
=150(平方厘米)
D,12×5×4+5×5×4
=240+100
=340(平方厘米)
480>340>150
答:最节省包装纸的是A。
故选:A。
二.填空题(共5小题)
8.如图所示的平面图形折叠成一个正方体,“会”字对面的字是 “运” 。
【解答】解:如图:
所示的平面图形折叠成一个正方体,“会”字对面的字是“运”。
故答案为:“运”。
9.长方体中,相交于一个顶点的三条棱的长度分别是7分米,5分米,4分米,要用铁丝围一个这样的长方体框架,需要铁丝 64 分米。(接头处忽略不计)
【解答】解:(7+5+4)×4
=16×4
=64(分米)
答:需要铁丝64分米。
故答案为:64。
10.用一根长36cm的铁丝做一个宽是2cm,高是3cm的长方体框架,这个框架的长是 4 cm,如做成一个正方体,正方体一个面的面积是 9 cm2
【解答】解:36÷4=9(厘米)
9﹣2﹣3=4(厘米)
36÷12=3(厘米)
3×3=9(平方厘米)
答:这个框架的长是4cm,如做成一个正方体,正方体一个面的面积是9cm2。
故答案为:4;36。
11.把一个表面积是100平方分米的长方体,参照右图切三次,切后的表面积之和比原来增加了 100 平方分米。
【解答】解:与长方体的上下面平行且一次,表面积增加上下面的面积;与长方体的前后面平行且一次,表面积增加前后面的面积,与长方体的左右面平行切一次,表面积增加左右面的面积。
所以,把一个表面积是100平方分米的长方体,参照右图切三次,切后的表面积之和比原来增加了100平方分米。
故答案为:100。
12.把一个长是6dm的长方体按右面三种方法分割成两个相同的小长方体,两个小长方体的表面积之和分别比原来长方体的表面积增加了48dm2、36dm2、24dm2,原来长方体的宽是 3 dm,高是 4 dm。
【解答】解:48÷2÷6
=24÷6
=4(分米)
36÷2÷6
=18÷6
=3(分米)
答:原来长方体的宽是3分米,高是4分米。
故答案为:3,4。
三.判断题(共4小题)
13.正方体是长、宽、高都相等的长方体。 √
【解答】解:长方体和正方体都有6个面,12条棱,8个顶点.
因此正方体可以看作长、宽、高都相等的长方体.
故答案为:√.
14.有6个面,8个顶点,12条棱的物体都是长方体. × .
【解答】解:如图就有8个顶点,12条棱,6个面的物体,不是长方体,也不是正方体,所以原题说法错误.
故答案为:×.
15.在同一位置看一个长方体,最多只能看到它的三个面. √ .
【解答】解:在一个观察点观察长方体最多可以看到它的三个面,由此,在同一位置看一个长方体,最多只能看到它的三个面.这种说法是正确的.
故答案为:√.
16.一个正方体的棱长总和是72dm,它的表面积是216dm2。 √
【解答】解:72÷12=6(分米)
6×6×6
=36×6
=216(平方分米)
所以它的表面积是216平方分米。
因此题干中的结论是正确的。
故答案为:√。
四.计算题(共2小题)
17.计算下面长方体和正方体的表面积。
(1)
(2)
【解答】解:(1)10×10×6
=100×6
=600(平方厘米)
答:这个正方体的表面积是600平方厘米。
(2)(20×13+20×5+13×5)×2
=(260+100+65)×2
=425×2
=850(平方厘米)
答:这个长方体的表面积是850平方厘米。
18.如图是长方体的展开图,求这个长方体的表面积。
【解答】解:高:(28﹣10×2)÷2
=(28﹣20)÷2
=8÷2
=4(厘米)
(10×6+10×4+6×4)×2
=(60+40+24)×2
=124×2
=248(平方厘米)
答:这个长方体的表面积是248平方厘米。
五.应用题(共5小题)
19.给一台棱长10分米的正方体冰箱做一个无底防尘布罩,至少需要多少平方分米布?
【解答】解:10×10×5
=100×5
=500(平方分米)
答:至少需要500平方分米布。
20.一个正方体礼品盒,棱长1.2分米,如果包装这个礼品盒用的纸是其表面积的1.5倍,至少要用多少平方分米的包装纸?
【解答】解:1.2×1.2×6×1.5
=1.44×6×1.5
=8.64×1.5
=12.96(平方分米)
答:至少要用12.96平方分米的包装纸。
21.一根铁丝刚好围成一个棱长10cm的正方体框架,如果把它改围成一个长12cm,宽7cm的长方体框架,长方体框架的高是多少厘米?
【解答】解;10×12=120(厘米)
120÷4﹣12﹣7
=30﹣12﹣7
=11(厘米)
答:长方体的高是11厘米.
22.某小学要粉刷新教室,除地板与门窗外,其余都要粉刷。已知教室的长是8m,宽6m,高4m,门窗的面积是12.5m2。如果每平方米需要花4元涂料费,粉刷这个教室需要花费多少钱?
【解答】解:(8×6+8×4×2+6×4×2﹣12.5)×4
=(48+64+48﹣12.5)×4
=(160﹣12.5)×4
=147.5×4
=590(元)
答:粉刷这个教室需要花费590元。
23.一个小长方体长3cm,宽2cm,高1cm,把三个这样的小长方体拼成一个大长方体,在大长方体的表面刷一层油漆,刷油漆的面积最少是多少?
长/cm 宽/cm 高/cm 表面积/cm2
9 2 1 58
3 6 1 54
3 2 3 42
【解答】解:(1)拼成一个长(3×3)厘米,宽是2厘米,高是1厘米的长方体。
(9×2+9×1+2×1)×2
=(18+9+2)×2
=29×2
=58(平方厘米)
(2)拼成一个长3厘米,宽(2×3)厘米,高是1厘米的长方体。
(3×6+3×1+6×1)×2
=(18+3+6)×2
=27×2
=54(平方厘米)
(3)拼成一个长3厘米,宽是2厘米高是(1×3)厘米的长方体。
(3×2+3×3+2×3)×2
=(6+9+6)×2
=21×2
=42(平方厘米)
42<54<58
答:第③种方油漆的面积最少,是42平方厘米。
故答案为:9,2,1,58;3,6,1,54;3,2,3,42。
一.选择题(共7小题)
1.长方体(不含正方体)的六个面中,最多有( )个面的面积相等。
A.6 B.4 C.3 D.2
2.加工一套空调外机的包装箱要用多少材料,是求包装箱的( )
A.表面积 B.体积 C.容积 D.棱长总和
3.用一根长1m的铁丝,正好能焊接成长10cm,宽5cm,高( )cm的长方体。
A.40 B.8 C.10 D.15
4.如图:将如图的纸片折起来可以做成一个正方体.这个正方体的6号面的对面是( )号面.
A.2 B.3 C.4
5.将展开图围成正方体后,标有“冬”字的那面就会与标有“( )”字的面相对。
A.春 B.夏 C.秋 D.季
6.从一个体积是30m3的长方体木块中挖掉一小块后(如图),它的表面积( )
A.比原来大 B.比原来小
C.和原来一样大 D.无法确定
7.笑笑把4盒长12cm,宽和高都是5cm的长方体礼品包装在一起,下面4种方法中,最节省包装纸的是( )
A.
B.
C.
D.
二.填空题(共5小题)
8.如图所示的平面图形折叠成一个正方体,“会”字对面的字是 。
9.长方体中,相交于一个顶点的三条棱的长度分别是7分米,5分米,4分米,要用铁丝围一个这样的长方体框架,需要铁丝 分米。(接头处忽略不计)
10.用一根长36cm的铁丝做一个宽是2cm,高是3cm的长方体框架,这个框架的长是 cm,如做成一个正方体,正方体一个面的面积是 cm2
11.把一个表面积是100平方分米的长方体,参照右图切三次,切后的表面积之和比原来增加了 平方分米。
12.把一个长是6dm的长方体按右面三种方法分割成两个相同的小长方体,两个小长方体的表面积之和分别比原来长方体的表面积增加了48dm2、36dm2、24dm2,原来长方体的宽是 dm,高是 dm。
三.判断题(共4小题)
13.正方体是长、宽、高都相等的长方体。
14.有6个面,8个顶点,12条棱的物体都是长方体. .
15.在同一位置看一个长方体,最多只能看到它的三个面. .
16.一个正方体的棱长总和是72dm,它的表面积是216dm2。
四.计算题(共2小题)
17.计算下面长方体和正方体的表面积。
(1)
(2)
18.如图是长方体的展开图,求这个长方体的表面积。
五.应用题(共5小题)
19.给一台棱长10分米的正方体冰箱做一个无底防尘布罩,至少需要多少平方分米布?
20.一个正方体礼品盒,棱长1.2分米,如果包装这个礼品盒用的纸是其表面积的1.5倍,至少要用多少平方分米的包装纸?
21.一根铁丝刚好围成一个棱长10cm的正方体框架,如果把它改围成一个长12cm,宽7cm的长方体框架,长方体框架的高是多少厘米?
22.某小学要粉刷新教室,除地板与门窗外,其余都要粉刷。已知教室的长是8m,宽6m,高4m,门窗的面积是12.5m2。如果每平方米需要花4元涂料费,粉刷这个教室需要花费多少钱?
23.一个小长方体长3cm,宽2cm,高1cm,把三个这样的小长方体拼成一个大长方体,在大长方体的表面刷一层油漆,刷油漆的面积最少是多少?
长/cm 宽/cm 高/cm 表面积/cm2
(基础篇)2023-2024学年下学期小学数学北师大新版五年级第二单元练习卷
参考答案与试题解析
一.选择题(共7小题)
1.长方体(不含正方体)的六个面中,最多有( )个面的面积相等。
A.6 B.4 C.3 D.2
【解答】解:在长方体中如果有两个相对的面是正方形,那么它的4个侧面是完全相同的长方形;
因此,长方体(不包括正方体)的六个面中,最多有4个的面积相等。
故选:B。
2.加工一套空调外机的包装箱要用多少材料,是求包装箱的( )
A.表面积 B.体积 C.容积 D.棱长总和
【解答】解:根据题干可得,
加工一套空调外机的包装箱要用多少材料,是求包装箱的表面积。
故选:A。
3.用一根长1m的铁丝,正好能焊接成长10cm,宽5cm,高( )cm的长方体。
A.40 B.8 C.10 D.15
【解答】解:1m=100cm
100÷4﹣(10+5)
=25﹣15
=10(厘米)
答:用一根长1m的铁丝,正好能焊接成长10cm,宽5cm,高10厘米的长方体。
故选:C。
4.如图:将如图的纸片折起来可以做成一个正方体.这个正方体的6号面的对面是( )号面.
A.2 B.3 C.4
【解答】解:纸片折起来可以做成一个正方体后:3号面对2号面,1号面对5号面,4号面对6号面.
故选:C。
5.将展开图围成正方体后,标有“冬”字的那面就会与标有“( )”字的面相对。
A.春 B.夏 C.秋 D.季
【解答】解:将展开图围成正方体后,标有“冬”字的那面就会与标有“春”字的面相对。
故选:A。
6.从一个体积是30m3的长方体木块中挖掉一小块后(如图),它的表面积( )
A.比原来大 B.比原来小
C.和原来一样大 D.无法确定
【解答】解:从一个体积是30m3的长方体木块中挖掉一小块后,它的表面积比原来大。
故选:A。
7.笑笑把4盒长12cm,宽和高都是5cm的长方体礼品包装在一起,下面4种方法中,最节省包装纸的是( )
A.
B.
C.
D.
【解答】解:A、12×5×8
=60×8
=480(平方厘米)
B、12×5×4+5×5×4
=240+100
=340(平方厘米)
C、5×5×6
=25×6
=150(平方厘米)
D,12×5×4+5×5×4
=240+100
=340(平方厘米)
480>340>150
答:最节省包装纸的是A。
故选:A。
二.填空题(共5小题)
8.如图所示的平面图形折叠成一个正方体,“会”字对面的字是 “运” 。
【解答】解:如图:
所示的平面图形折叠成一个正方体,“会”字对面的字是“运”。
故答案为:“运”。
9.长方体中,相交于一个顶点的三条棱的长度分别是7分米,5分米,4分米,要用铁丝围一个这样的长方体框架,需要铁丝 64 分米。(接头处忽略不计)
【解答】解:(7+5+4)×4
=16×4
=64(分米)
答:需要铁丝64分米。
故答案为:64。
10.用一根长36cm的铁丝做一个宽是2cm,高是3cm的长方体框架,这个框架的长是 4 cm,如做成一个正方体,正方体一个面的面积是 9 cm2
【解答】解:36÷4=9(厘米)
9﹣2﹣3=4(厘米)
36÷12=3(厘米)
3×3=9(平方厘米)
答:这个框架的长是4cm,如做成一个正方体,正方体一个面的面积是9cm2。
故答案为:4;36。
11.把一个表面积是100平方分米的长方体,参照右图切三次,切后的表面积之和比原来增加了 100 平方分米。
【解答】解:与长方体的上下面平行且一次,表面积增加上下面的面积;与长方体的前后面平行且一次,表面积增加前后面的面积,与长方体的左右面平行切一次,表面积增加左右面的面积。
所以,把一个表面积是100平方分米的长方体,参照右图切三次,切后的表面积之和比原来增加了100平方分米。
故答案为:100。
12.把一个长是6dm的长方体按右面三种方法分割成两个相同的小长方体,两个小长方体的表面积之和分别比原来长方体的表面积增加了48dm2、36dm2、24dm2,原来长方体的宽是 3 dm,高是 4 dm。
【解答】解:48÷2÷6
=24÷6
=4(分米)
36÷2÷6
=18÷6
=3(分米)
答:原来长方体的宽是3分米,高是4分米。
故答案为:3,4。
三.判断题(共4小题)
13.正方体是长、宽、高都相等的长方体。 √
【解答】解:长方体和正方体都有6个面,12条棱,8个顶点.
因此正方体可以看作长、宽、高都相等的长方体.
故答案为:√.
14.有6个面,8个顶点,12条棱的物体都是长方体. × .
【解答】解:如图就有8个顶点,12条棱,6个面的物体,不是长方体,也不是正方体,所以原题说法错误.
故答案为:×.
15.在同一位置看一个长方体,最多只能看到它的三个面. √ .
【解答】解:在一个观察点观察长方体最多可以看到它的三个面,由此,在同一位置看一个长方体,最多只能看到它的三个面.这种说法是正确的.
故答案为:√.
16.一个正方体的棱长总和是72dm,它的表面积是216dm2。 √
【解答】解:72÷12=6(分米)
6×6×6
=36×6
=216(平方分米)
所以它的表面积是216平方分米。
因此题干中的结论是正确的。
故答案为:√。
四.计算题(共2小题)
17.计算下面长方体和正方体的表面积。
(1)
(2)
【解答】解:(1)10×10×6
=100×6
=600(平方厘米)
答:这个正方体的表面积是600平方厘米。
(2)(20×13+20×5+13×5)×2
=(260+100+65)×2
=425×2
=850(平方厘米)
答:这个长方体的表面积是850平方厘米。
18.如图是长方体的展开图,求这个长方体的表面积。
【解答】解:高:(28﹣10×2)÷2
=(28﹣20)÷2
=8÷2
=4(厘米)
(10×6+10×4+6×4)×2
=(60+40+24)×2
=124×2
=248(平方厘米)
答:这个长方体的表面积是248平方厘米。
五.应用题(共5小题)
19.给一台棱长10分米的正方体冰箱做一个无底防尘布罩,至少需要多少平方分米布?
【解答】解:10×10×5
=100×5
=500(平方分米)
答:至少需要500平方分米布。
20.一个正方体礼品盒,棱长1.2分米,如果包装这个礼品盒用的纸是其表面积的1.5倍,至少要用多少平方分米的包装纸?
【解答】解:1.2×1.2×6×1.5
=1.44×6×1.5
=8.64×1.5
=12.96(平方分米)
答:至少要用12.96平方分米的包装纸。
21.一根铁丝刚好围成一个棱长10cm的正方体框架,如果把它改围成一个长12cm,宽7cm的长方体框架,长方体框架的高是多少厘米?
【解答】解;10×12=120(厘米)
120÷4﹣12﹣7
=30﹣12﹣7
=11(厘米)
答:长方体的高是11厘米.
22.某小学要粉刷新教室,除地板与门窗外,其余都要粉刷。已知教室的长是8m,宽6m,高4m,门窗的面积是12.5m2。如果每平方米需要花4元涂料费,粉刷这个教室需要花费多少钱?
【解答】解:(8×6+8×4×2+6×4×2﹣12.5)×4
=(48+64+48﹣12.5)×4
=(160﹣12.5)×4
=147.5×4
=590(元)
答:粉刷这个教室需要花费590元。
23.一个小长方体长3cm,宽2cm,高1cm,把三个这样的小长方体拼成一个大长方体,在大长方体的表面刷一层油漆,刷油漆的面积最少是多少?
长/cm 宽/cm 高/cm 表面积/cm2
9 2 1 58
3 6 1 54
3 2 3 42
【解答】解:(1)拼成一个长(3×3)厘米,宽是2厘米,高是1厘米的长方体。
(9×2+9×1+2×1)×2
=(18+9+2)×2
=29×2
=58(平方厘米)
(2)拼成一个长3厘米,宽(2×3)厘米,高是1厘米的长方体。
(3×6+3×1+6×1)×2
=(18+3+6)×2
=27×2
=54(平方厘米)
(3)拼成一个长3厘米,宽是2厘米高是(1×3)厘米的长方体。
(3×2+3×3+2×3)×2
=(6+9+6)×2
=21×2
=42(平方厘米)
42<54<58
答:第③种方油漆的面积最少,是42平方厘米。
故答案为:9,2,1,58;3,6,1,54;3,2,3,42。
