第二单元练习卷(单元测试)小学数学五年级下册 北师大版(进阶篇)(含答案)
文档属性
| 名称 | 第二单元练习卷(单元测试)小学数学五年级下册 北师大版(进阶篇)(含答案) |  | |
| 格式 | Doc | ||
| 文件大小 | 364.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-17 20:35:25 | ||
图片预览



文档简介
(进阶篇)2023-2024学年下学期小学数学北师大新版五年级第二单元练习卷
一.选择题(共8小题)
1.下面的图形,( )不是正方体的展开图。
A. B. C. D.
2.如图,是正方体表面展开图,“爱”字相对的字是( )
A.的 B.祖 C.国
3.根据如图所给的数据,想象一下这个长方体可能是( )
A.数学书 B.橡皮 C.米尺 D.粉笔盒
4.一根长56分米的铁丝,可以焊成一个长5分米,宽( )分米,高3分米的长方体框架。
A.3 B.4 C.5 D.6
5.如图,一个由8个小正方体拼成的大正方体,如果去掉一个小正方体后,得到的图形的表面积与原来的表面积相比,( )
A.变小了 B.变大了 C.相等
6.把两个棱长为4厘米的正方体拼成一个长方体,表面积减少了( )平方厘米。
A.16 B.32 C.48 D.60
7.如图,将一个长12厘米,宽6厘米,高2厘米的长方体木块锯成三个相同的小长方体,木块的表面积增加了( )平方厘米。
A.48 B.24 C.18 D.36
8.小明用橡皮泥做了一个棱长5厘米的实心正方体,从这个正方体上挖出一个棱长2厘米的小正方体,下面关于原来大正方体的表面积的说法中,错误的是( )
A.可能不变 B.最多增加16平方厘米
C.可能增加4平方厘米 D.可能增加8平方厘米
二.填空题(共7小题)
9.用一个长方体积木的面,最多能画出 种不同的长方形。
10.一个长方体长7cm,宽5cm,高4cm,它的表面积是 cm2,它的棱长总和是 cm。
11.把一个长方体切分成两个完全一样的小正方体,表面积增加了32cm2,原来长方体的表面积是 cm2。
12.若一个正方体的棱长为4dm,现在将棱长扩大到原来的2倍,则其棱长总和增加 dm,表面积增加 dm2。
13.一个长方体的底面是一个面积为2平方分米的正方形,它的侧面展开图正好是一个正方形,这个长方体的侧面积 平方分米。
14.用两个棱长是5分米的正方体拼成一个长方体,拼成的长方体的表面积是 平方分米。
15.将一个长9分米、宽6厘米、高5分米的长方体木块从中间截开,可以截成形状相同的两个小长方体。截开后,表面积最多增加 。
三.判断题(共5小题)
16.正方体的六个面都是正方形. .
17.在一个长方体中,相对的棱长度相等,相对的面完全相同。
18.长方体的长、宽、高都扩大到原来的2倍,则棱长总和也扩大到原来的2倍。
19.用铁丝制作一个棱长是5厘米的正方体框架,至少需要150厘米铁丝.
20.将一个长方体刚好切成两个相等的正方体,每个正方体的表面积是长方体表面积的一半. .
四.操作题(共3小题)
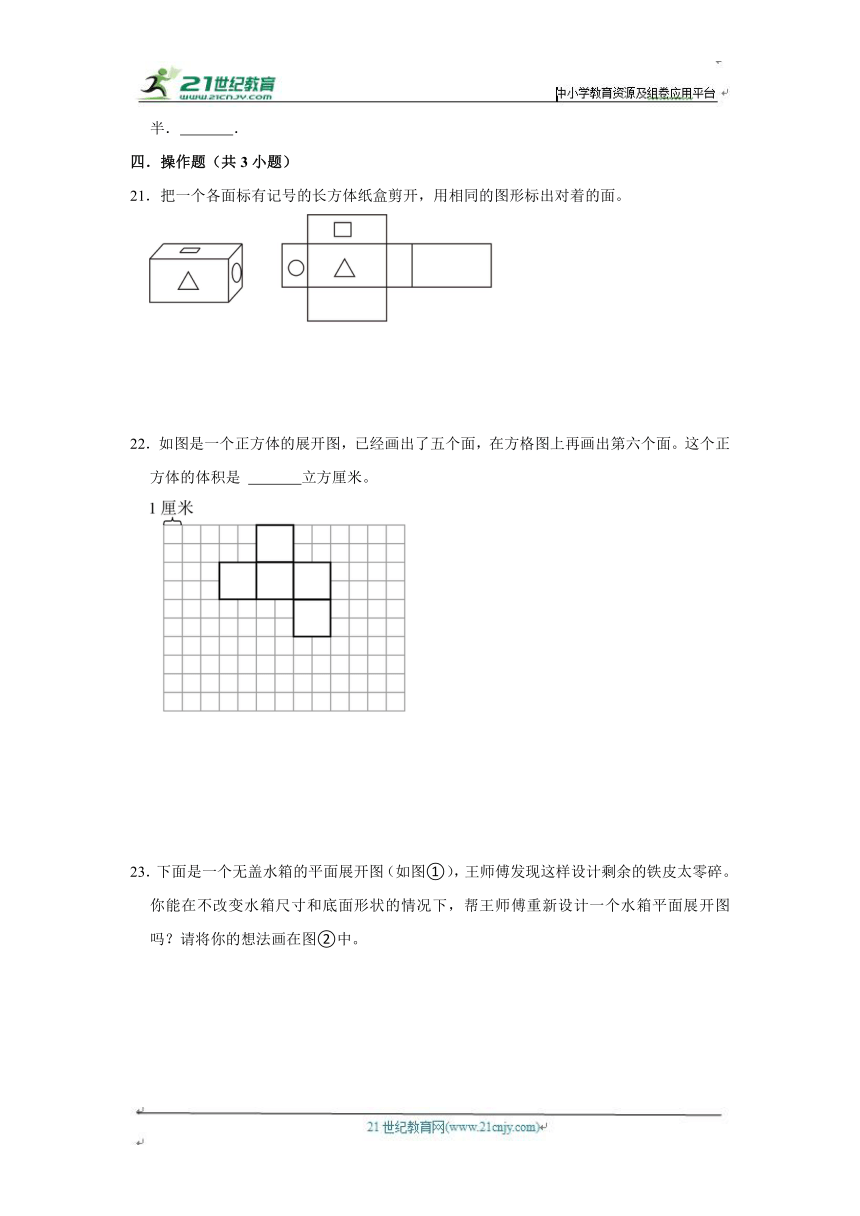
21.把一个各面标有记号的长方体纸盒剪开,用相同的图形标出对着的面。
22.如图是一个正方体的展开图,已经画出了五个面,在方格图上再画出第六个面。这个正方体的体积是 立方厘米。
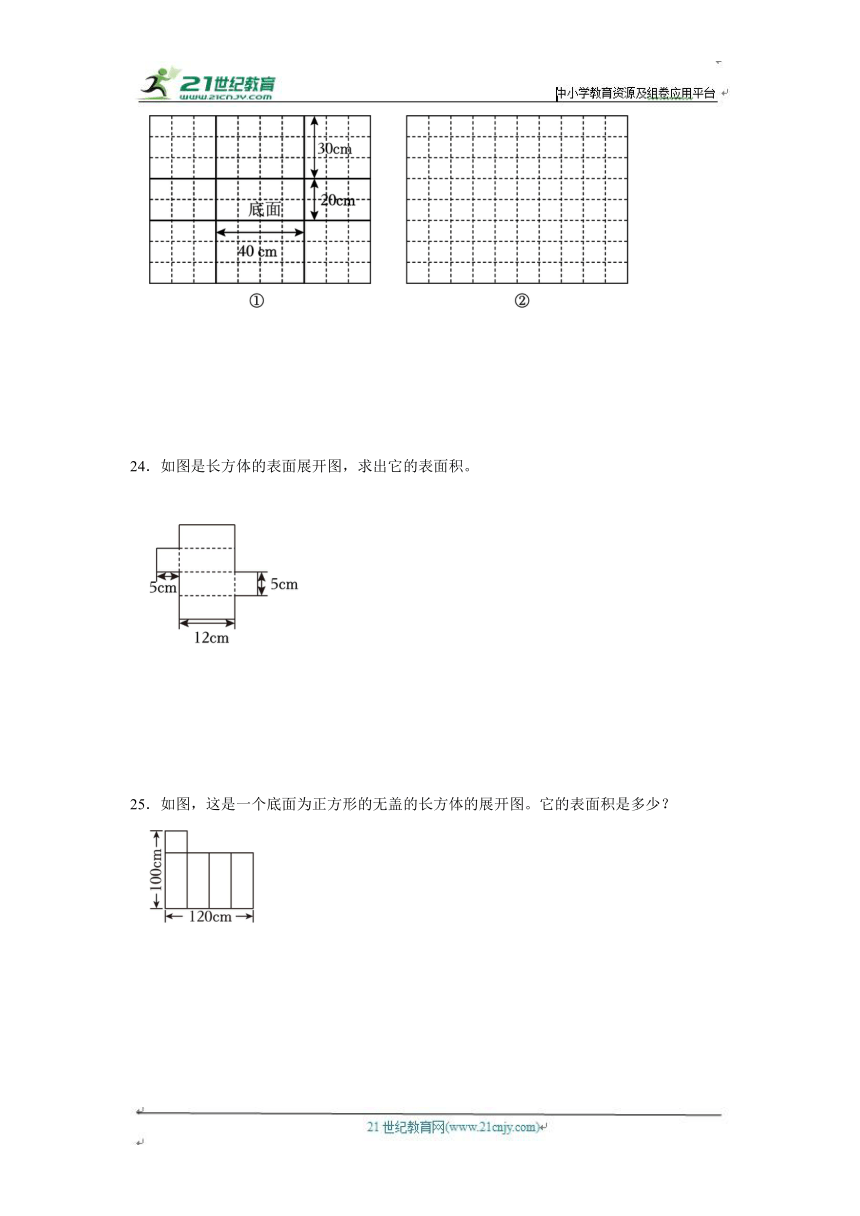
23.下面是一个无盖水箱的平面展开图(如图①),王师傅发现这样设计剩余的铁皮太零碎。你能在不改变水箱尺寸和底面形状的情况下,帮王师傅重新设计一个水箱平面展开图吗?请将你的想法画在图②中。
24.如图是长方体的表面展开图,求出它的表面积。
25.如图,这是一个底面为正方形的无盖的长方体的展开图。它的表面积是多少?
(进阶篇)2023-2024学年下学期小学数学北师大新版五年级第二单元练习卷
参考答案与试题解析
一.选择题(共8小题)
1.下面的图形,( )不是正方体的展开图。
A. B. C. D.
【解答】解:图B、图C和图D都是正方体的展开图,能折成正方体,图A不属于正方体的展开图,不能折成正方体。
故选:A。
2.如图,是正方体表面展开图,“爱”字相对的字是( )
A.的 B.祖 C.国
【解答】解:
是正方体表面展开图,相“爱”字相对的字是“祖”。
故选:B。
3.根据如图所给的数据,想象一下这个长方体可能是( )
A.数学书 B.橡皮 C.米尺 D.粉笔盒
【解答】解:根据分析可知这个长方体可能是数学书。
故选:A。
4.一根长56分米的铁丝,可以焊成一个长5分米,宽( )分米,高3分米的长方体框架。
A.3 B.4 C.5 D.6
【解答】解:56÷4﹣(5+3)
=14﹣8
=6(分米)
答:宽是6分米。
故选:D。
5.如图,一个由8个小正方体拼成的大正方体,如果去掉一个小正方体后,得到的图形的表面积与原来的表面积相比,( )
A.变小了 B.变大了 C.相等
【解答】解:由分析可知:八个小正方体拼成一个大正方体,若去掉一个小正方体,减少了三个小正方形的面,同时又增加了三个小正方形的面积,所以得到图形的表面积与原来正方体的表面积相等。
故选:C。
6.把两个棱长为4厘米的正方体拼成一个长方体,表面积减少了( )平方厘米。
A.16 B.32 C.48 D.60
【解答】解:4×4×2
=16×2
=32(平方厘米)
答:表面积减少了32平方厘米。
故选:B。
7.如图,将一个长12厘米,宽6厘米,高2厘米的长方体木块锯成三个相同的小长方体,木块的表面积增加了( )平方厘米。
A.48 B.24 C.18 D.36
【解答】解:6×2×4
=12×4
=48(平方厘米)
答:木块的表面积增加了48平方厘米。
故选:A。
8.小明用橡皮泥做了一个棱长5厘米的实心正方体,从这个正方体上挖出一个棱长2厘米的小正方体,下面关于原来大正方体的表面积的说法中,错误的是( )
A.可能不变 B.最多增加16平方厘米
C.可能增加4平方厘米 D.可能增加8平方厘米
【解答】解:由分析得:
A、可能不变。说法正确;
B、最多增加16平方厘米。说法正确;
C、可能增加4平方厘米。说法错误;
D、可能增加8平方厘米。说法正确。
故选:C。
二.填空题(共7小题)
9.用一个长方体积木的面,最多能画出 3 种不同的长方形。
【解答】解:因为长方体相对面是完全相同的长方形,长方体有6个面,所以用一个长方体积木的面,最多能画出3种不同的长方形。
故答案为:3。
10.一个长方体长7cm,宽5cm,高4cm,它的表面积是 166 cm2,它的棱长总和是 64 cm。
【解答】解:(7×5+7×4+5×4)×2
=(35+28+20)×2
=83×2
=166(平方厘米)
(7+5+4)×4
=16×4
=64(厘米)
答:它的表面积是166cm2,它的棱长总和是64cm。
故答案为:166,64。
11.把一个长方体切分成两个完全一样的小正方体,表面积增加了32cm2,原来长方体的表面积是 128 cm2。
【解答】解:32÷2×8
=16×8
=128(平方厘米)
答:原来长方体的表面积是128平方厘米。
故答案为:128。
12.若一个正方体的棱长为4dm,现在将棱长扩大到原来的2倍,则其棱长总和增加 48 dm,表面积增加 288 dm2。
【解答】解:4×2×12﹣4×12
=8×12﹣48
=96﹣48
=48(分米)
(4×2)×(4×2)×6﹣4×4×6
=8×8×6﹣96
=64×6﹣96
=384﹣96
=288(平方分米)
答:其棱长总和增加48dm,表面积增加288dm2。
故答案为:48,288。
13.一个长方体的底面是一个面积为2平方分米的正方形,它的侧面展开图正好是一个正方形,这个长方体的侧面积 32 平方分米。
【解答】解:结合长方体的侧面是一个正方形的特征,以及题目里具体的数据可得:
16×2=32(平方分米)
答:这个长方体的侧面积32平方分米。
故答案为:32。
14.用两个棱长是5分米的正方体拼成一个长方体,拼成的长方体的表面积是 250 平方分米。
【解答】解:5×5×6×2﹣5×5×2
=25×6×2﹣25×2
=150×2﹣50
=300﹣50
=250(平方分米)
答:拼成的长方体的表面积是250平方分米。
故答案为:250。
15.将一个长9分米、宽6厘米、高5分米的长方体木块从中间截开,可以截成形状相同的两个小长方体。截开后,表面积最多增加 90平方分米 。
【解答】解:9×5×2
=45×2
=90(平方分米)
答:表面积最多增加90平方分米。
故答案为:90平方分米。
三.判断题(共5小题)
16.正方体的六个面都是正方形. √ .
【解答】解:正方体的六个面都是正方形.
原题说法正确.
故答案为:√.
17.在一个长方体中,相对的棱长度相等,相对的面完全相同。 √
【解答】解:在一个长方体中,相对的棱长度相等,相对的面完全相同。说法正确。
故答案为:√。
18.长方体的长、宽、高都扩大到原来的2倍,则棱长总和也扩大到原来的2倍。 √
【解答】解:一个长方体的长、宽、高都扩大2倍,它的棱长总和就扩大到原来的2倍,原题说法正确。
故答案为:√。
19.用铁丝制作一个棱长是5厘米的正方体框架,至少需要150厘米铁丝. ×
【解答】解:5×12=60(厘米),
所以至少需要铁丝60厘米.
可见上面的说法错误.
故答案为:×.
20.将一个长方体刚好切成两个相等的正方体,每个正方体的表面积是长方体表面积的一半. × .
【解答】解:设正方体的棱长是a,正方体的表面积是:a×a×6=6a2;长方体的表面积是:a×a×2+2a×a×4=10a2.
所以每个正方体的表面积是长方体表面积的一半,是不对的.
故答案为:×.
四.操作题(共3小题)
21.把一个各面标有记号的长方体纸盒剪开,用相同的图形标出对着的面。
【解答】解:长方体的前后相对的两个面都是△,上下相对的两个面都是□,左右相对的两个面都是〇,由此作图:
。
22.如图是一个正方体的展开图,已经画出了五个面,在方格图上再画出第六个面。这个正方体的体积是 8 立方厘米。
【解答】解:根据题意画图如下(画法不唯一):
23=2×2×2=8(立方厘米)
答:这个正方体的体积是8立方厘米。
故答案为:8。
23.下面是一个无盖水箱的平面展开图(如图①),王师傅发现这样设计剩余的铁皮太零碎。你能在不改变水箱尺寸和底面形状的情况下,帮王师傅重新设计一个水箱平面展开图吗?请将你的想法画在图②中。
【解答】解:由分析可得:
(答案不唯一)
五.解答题(共2小题)
24.如图是长方体的表面展开图,求出它的表面积。
【解答】解:(12×5+12×5+5×5)×2
=145×2
=290(cm2)
答:它的表面积是290平方厘米。
25.如图,这是一个底面为正方形的无盖的长方体的展开图。它的表面积是多少?
【解答】解:底面边长:120÷4=30(厘米)
故:100﹣30=70(厘米)
表面积:
30×30+30×70×2+30×70×2
=900+4200+4200
=9300(平方厘米)
答:它的表面积是9300平方厘米。
一.选择题(共8小题)
1.下面的图形,( )不是正方体的展开图。
A. B. C. D.
2.如图,是正方体表面展开图,“爱”字相对的字是( )
A.的 B.祖 C.国
3.根据如图所给的数据,想象一下这个长方体可能是( )
A.数学书 B.橡皮 C.米尺 D.粉笔盒
4.一根长56分米的铁丝,可以焊成一个长5分米,宽( )分米,高3分米的长方体框架。
A.3 B.4 C.5 D.6
5.如图,一个由8个小正方体拼成的大正方体,如果去掉一个小正方体后,得到的图形的表面积与原来的表面积相比,( )
A.变小了 B.变大了 C.相等
6.把两个棱长为4厘米的正方体拼成一个长方体,表面积减少了( )平方厘米。
A.16 B.32 C.48 D.60
7.如图,将一个长12厘米,宽6厘米,高2厘米的长方体木块锯成三个相同的小长方体,木块的表面积增加了( )平方厘米。
A.48 B.24 C.18 D.36
8.小明用橡皮泥做了一个棱长5厘米的实心正方体,从这个正方体上挖出一个棱长2厘米的小正方体,下面关于原来大正方体的表面积的说法中,错误的是( )
A.可能不变 B.最多增加16平方厘米
C.可能增加4平方厘米 D.可能增加8平方厘米
二.填空题(共7小题)
9.用一个长方体积木的面,最多能画出 种不同的长方形。
10.一个长方体长7cm,宽5cm,高4cm,它的表面积是 cm2,它的棱长总和是 cm。
11.把一个长方体切分成两个完全一样的小正方体,表面积增加了32cm2,原来长方体的表面积是 cm2。
12.若一个正方体的棱长为4dm,现在将棱长扩大到原来的2倍,则其棱长总和增加 dm,表面积增加 dm2。
13.一个长方体的底面是一个面积为2平方分米的正方形,它的侧面展开图正好是一个正方形,这个长方体的侧面积 平方分米。
14.用两个棱长是5分米的正方体拼成一个长方体,拼成的长方体的表面积是 平方分米。
15.将一个长9分米、宽6厘米、高5分米的长方体木块从中间截开,可以截成形状相同的两个小长方体。截开后,表面积最多增加 。
三.判断题(共5小题)
16.正方体的六个面都是正方形. .
17.在一个长方体中,相对的棱长度相等,相对的面完全相同。
18.长方体的长、宽、高都扩大到原来的2倍,则棱长总和也扩大到原来的2倍。
19.用铁丝制作一个棱长是5厘米的正方体框架,至少需要150厘米铁丝.
20.将一个长方体刚好切成两个相等的正方体,每个正方体的表面积是长方体表面积的一半. .
四.操作题(共3小题)
21.把一个各面标有记号的长方体纸盒剪开,用相同的图形标出对着的面。
22.如图是一个正方体的展开图,已经画出了五个面,在方格图上再画出第六个面。这个正方体的体积是 立方厘米。
23.下面是一个无盖水箱的平面展开图(如图①),王师傅发现这样设计剩余的铁皮太零碎。你能在不改变水箱尺寸和底面形状的情况下,帮王师傅重新设计一个水箱平面展开图吗?请将你的想法画在图②中。
24.如图是长方体的表面展开图,求出它的表面积。
25.如图,这是一个底面为正方形的无盖的长方体的展开图。它的表面积是多少?
(进阶篇)2023-2024学年下学期小学数学北师大新版五年级第二单元练习卷
参考答案与试题解析
一.选择题(共8小题)
1.下面的图形,( )不是正方体的展开图。
A. B. C. D.
【解答】解:图B、图C和图D都是正方体的展开图,能折成正方体,图A不属于正方体的展开图,不能折成正方体。
故选:A。
2.如图,是正方体表面展开图,“爱”字相对的字是( )
A.的 B.祖 C.国
【解答】解:
是正方体表面展开图,相“爱”字相对的字是“祖”。
故选:B。
3.根据如图所给的数据,想象一下这个长方体可能是( )
A.数学书 B.橡皮 C.米尺 D.粉笔盒
【解答】解:根据分析可知这个长方体可能是数学书。
故选:A。
4.一根长56分米的铁丝,可以焊成一个长5分米,宽( )分米,高3分米的长方体框架。
A.3 B.4 C.5 D.6
【解答】解:56÷4﹣(5+3)
=14﹣8
=6(分米)
答:宽是6分米。
故选:D。
5.如图,一个由8个小正方体拼成的大正方体,如果去掉一个小正方体后,得到的图形的表面积与原来的表面积相比,( )
A.变小了 B.变大了 C.相等
【解答】解:由分析可知:八个小正方体拼成一个大正方体,若去掉一个小正方体,减少了三个小正方形的面,同时又增加了三个小正方形的面积,所以得到图形的表面积与原来正方体的表面积相等。
故选:C。
6.把两个棱长为4厘米的正方体拼成一个长方体,表面积减少了( )平方厘米。
A.16 B.32 C.48 D.60
【解答】解:4×4×2
=16×2
=32(平方厘米)
答:表面积减少了32平方厘米。
故选:B。
7.如图,将一个长12厘米,宽6厘米,高2厘米的长方体木块锯成三个相同的小长方体,木块的表面积增加了( )平方厘米。
A.48 B.24 C.18 D.36
【解答】解:6×2×4
=12×4
=48(平方厘米)
答:木块的表面积增加了48平方厘米。
故选:A。
8.小明用橡皮泥做了一个棱长5厘米的实心正方体,从这个正方体上挖出一个棱长2厘米的小正方体,下面关于原来大正方体的表面积的说法中,错误的是( )
A.可能不变 B.最多增加16平方厘米
C.可能增加4平方厘米 D.可能增加8平方厘米
【解答】解:由分析得:
A、可能不变。说法正确;
B、最多增加16平方厘米。说法正确;
C、可能增加4平方厘米。说法错误;
D、可能增加8平方厘米。说法正确。
故选:C。
二.填空题(共7小题)
9.用一个长方体积木的面,最多能画出 3 种不同的长方形。
【解答】解:因为长方体相对面是完全相同的长方形,长方体有6个面,所以用一个长方体积木的面,最多能画出3种不同的长方形。
故答案为:3。
10.一个长方体长7cm,宽5cm,高4cm,它的表面积是 166 cm2,它的棱长总和是 64 cm。
【解答】解:(7×5+7×4+5×4)×2
=(35+28+20)×2
=83×2
=166(平方厘米)
(7+5+4)×4
=16×4
=64(厘米)
答:它的表面积是166cm2,它的棱长总和是64cm。
故答案为:166,64。
11.把一个长方体切分成两个完全一样的小正方体,表面积增加了32cm2,原来长方体的表面积是 128 cm2。
【解答】解:32÷2×8
=16×8
=128(平方厘米)
答:原来长方体的表面积是128平方厘米。
故答案为:128。
12.若一个正方体的棱长为4dm,现在将棱长扩大到原来的2倍,则其棱长总和增加 48 dm,表面积增加 288 dm2。
【解答】解:4×2×12﹣4×12
=8×12﹣48
=96﹣48
=48(分米)
(4×2)×(4×2)×6﹣4×4×6
=8×8×6﹣96
=64×6﹣96
=384﹣96
=288(平方分米)
答:其棱长总和增加48dm,表面积增加288dm2。
故答案为:48,288。
13.一个长方体的底面是一个面积为2平方分米的正方形,它的侧面展开图正好是一个正方形,这个长方体的侧面积 32 平方分米。
【解答】解:结合长方体的侧面是一个正方形的特征,以及题目里具体的数据可得:
16×2=32(平方分米)
答:这个长方体的侧面积32平方分米。
故答案为:32。
14.用两个棱长是5分米的正方体拼成一个长方体,拼成的长方体的表面积是 250 平方分米。
【解答】解:5×5×6×2﹣5×5×2
=25×6×2﹣25×2
=150×2﹣50
=300﹣50
=250(平方分米)
答:拼成的长方体的表面积是250平方分米。
故答案为:250。
15.将一个长9分米、宽6厘米、高5分米的长方体木块从中间截开,可以截成形状相同的两个小长方体。截开后,表面积最多增加 90平方分米 。
【解答】解:9×5×2
=45×2
=90(平方分米)
答:表面积最多增加90平方分米。
故答案为:90平方分米。
三.判断题(共5小题)
16.正方体的六个面都是正方形. √ .
【解答】解:正方体的六个面都是正方形.
原题说法正确.
故答案为:√.
17.在一个长方体中,相对的棱长度相等,相对的面完全相同。 √
【解答】解:在一个长方体中,相对的棱长度相等,相对的面完全相同。说法正确。
故答案为:√。
18.长方体的长、宽、高都扩大到原来的2倍,则棱长总和也扩大到原来的2倍。 √
【解答】解:一个长方体的长、宽、高都扩大2倍,它的棱长总和就扩大到原来的2倍,原题说法正确。
故答案为:√。
19.用铁丝制作一个棱长是5厘米的正方体框架,至少需要150厘米铁丝. ×
【解答】解:5×12=60(厘米),
所以至少需要铁丝60厘米.
可见上面的说法错误.
故答案为:×.
20.将一个长方体刚好切成两个相等的正方体,每个正方体的表面积是长方体表面积的一半. × .
【解答】解:设正方体的棱长是a,正方体的表面积是:a×a×6=6a2;长方体的表面积是:a×a×2+2a×a×4=10a2.
所以每个正方体的表面积是长方体表面积的一半,是不对的.
故答案为:×.
四.操作题(共3小题)
21.把一个各面标有记号的长方体纸盒剪开,用相同的图形标出对着的面。
【解答】解:长方体的前后相对的两个面都是△,上下相对的两个面都是□,左右相对的两个面都是〇,由此作图:
。
22.如图是一个正方体的展开图,已经画出了五个面,在方格图上再画出第六个面。这个正方体的体积是 8 立方厘米。
【解答】解:根据题意画图如下(画法不唯一):
23=2×2×2=8(立方厘米)
答:这个正方体的体积是8立方厘米。
故答案为:8。
23.下面是一个无盖水箱的平面展开图(如图①),王师傅发现这样设计剩余的铁皮太零碎。你能在不改变水箱尺寸和底面形状的情况下,帮王师傅重新设计一个水箱平面展开图吗?请将你的想法画在图②中。
【解答】解:由分析可得:
(答案不唯一)
五.解答题(共2小题)
24.如图是长方体的表面展开图,求出它的表面积。
【解答】解:(12×5+12×5+5×5)×2
=145×2
=290(cm2)
答:它的表面积是290平方厘米。
25.如图,这是一个底面为正方形的无盖的长方体的展开图。它的表面积是多少?
【解答】解:底面边长:120÷4=30(厘米)
故:100﹣30=70(厘米)
表面积:
30×30+30×70×2+30×70×2
=900+4200+4200
=9300(平方厘米)
答:它的表面积是9300平方厘米。
