二次函数复习

课件26张PPT。二次函数复习1返回
通过对实际问题情境的分析确定二次会用描点法画二次函数的图象，能从图象上认识二次函数的性质。会根据公式确定图象的顶点、开口方向和对称轴（公式不要求推导和记忆），并能解决简单的实际问题。会利用二次函数的图象求一元二次、二元一次方程组的近似值。函数的表达式，体会二次函数的意义新课标内容解读1返回
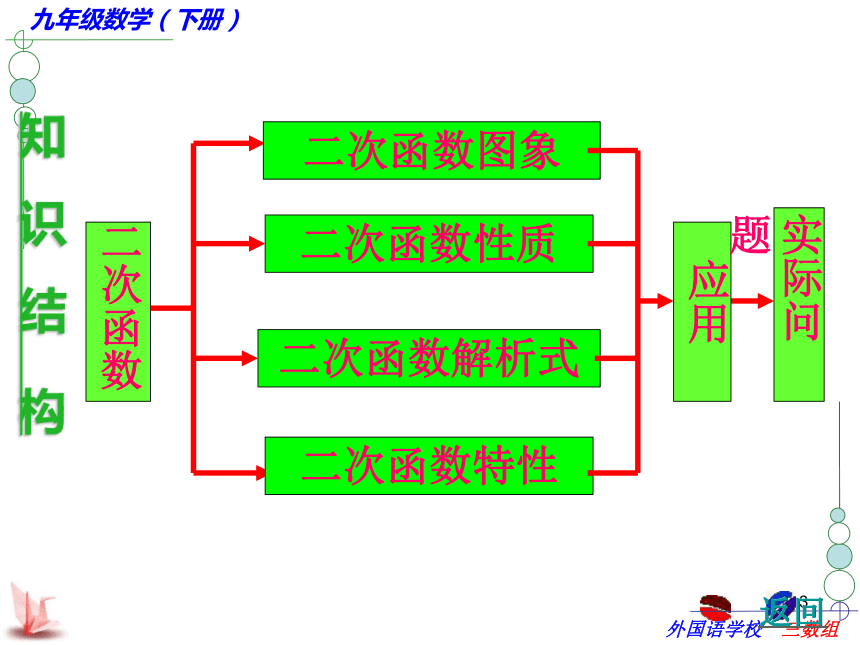
二次函数二次函数图象二次函数性质二次函数特性二次函数解析式应用实际问题知 识 结 构1一、二次函数的定义 1.定义：y=ax2+bx+c(a,b,c是常数,a≠0)2.定义要点:
(1)a≠0. (2)最高次数为2. (3)代数式一定是整式.2-21下列函数中,哪些是二次函数?辨一辨是不是是是不是11、二次函数 y=-x2+58x-112 的
二次项系数为 ，
一次项系数为 ，
常数项 。
2、二次函数y=πx2的
二次项系 数 ,
一次项系数 ，
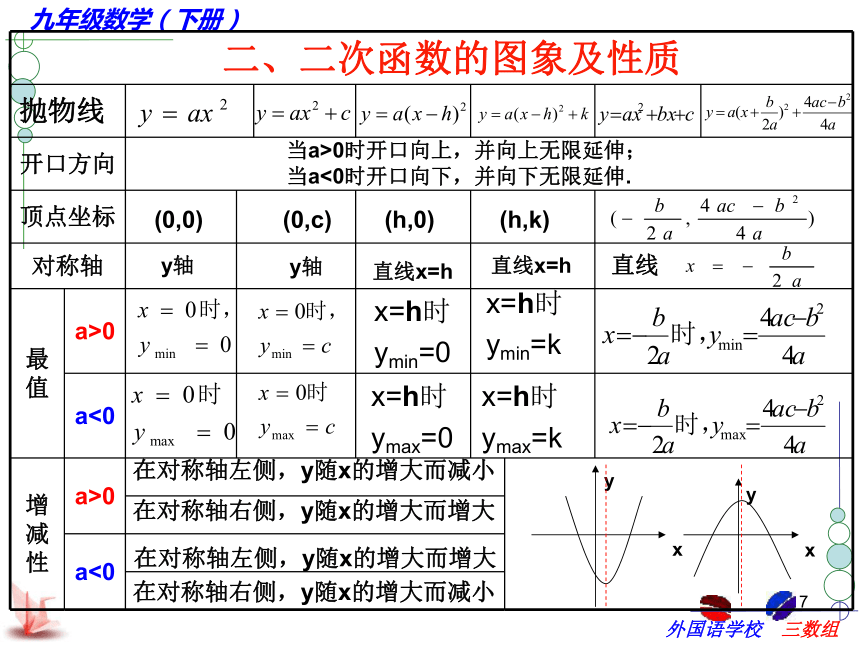
常数项 。a=-1b=58c=-112a=πb=0c=0填一填1二、二次函数的图象及性质当a>0时开口向上，并向上无限延伸；
当a<0时开口向下，并向下无限延伸.(0,0)(0,c)(h,0)(h,k)y轴在对称轴左侧，y随x的增大而减小在对称轴右侧，y随x的增大而增大在对称轴左侧，y随x的增大而增大在对称轴右侧，y随x的增大而减小y轴直线x=h直线x=hx=h时
ymin=0x=h时
ymax=0x=h时
ymin=kx=h时
ymax=k1返回
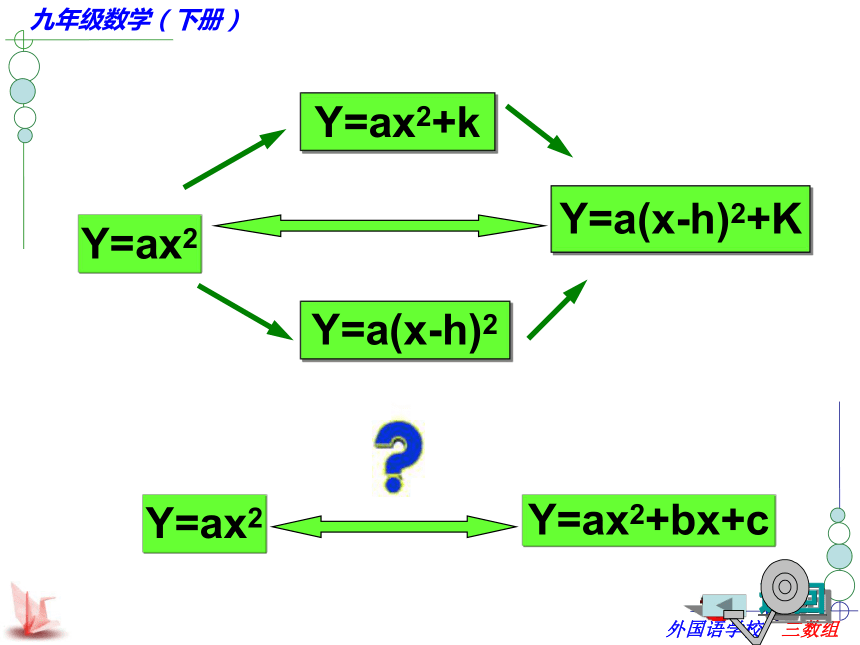
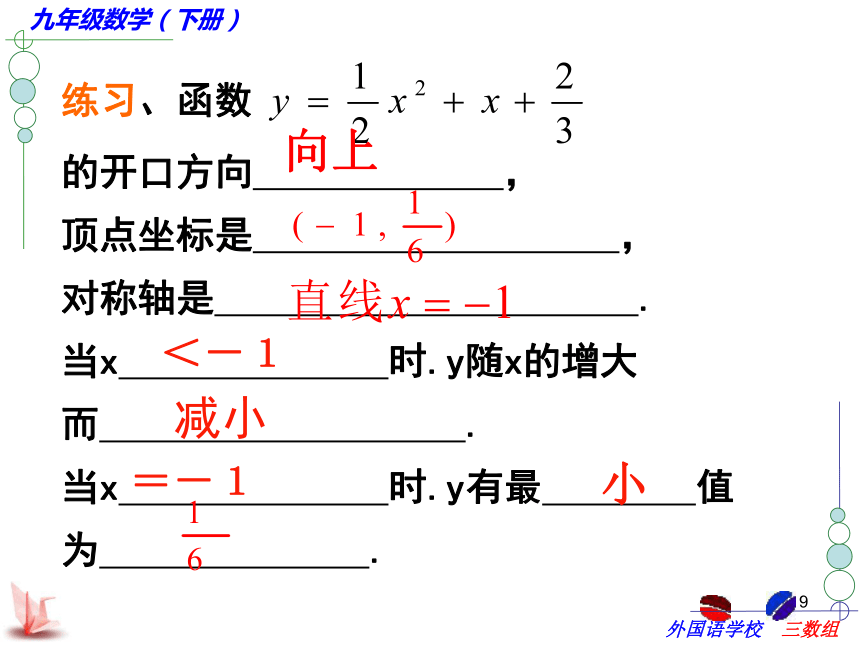
Y=ax2Y=ax2+kY=a(x-h)2Y=a(x-h)2+KY=ax2Y=ax2+bx+c1练习、函数 　　　　
的开口方向 ，
顶点坐标是 ，
对称轴是 　　 .
当x 　 时.y随x的增大
而 　 .
当x 　 时.y有最　　　　值
为 . 向上＜－１减小＝－１小1三、抛物线的平移法则加向上减向下，加向左减向右1、将抛物线y=-3x2-1向上平移2个单位, 再向右平移 3个单位, 所得的抛物线的表达式为 　　　　 ，2.若把抛物线y=x2+bx+c向左平移3个单位,再向上平移2个单位,得抛物线y=x2-2x+2,
则b= ，c= ,-8151二次函数y=ax2+bx+c(a≠0)的系数a，b，c与图象的关系a决定开口方向：a＞０时,开口向上，a＜０时,开口向下 a、b同时决定对称轴位置：a、b同号时对称轴在y轴左侧
　　　　　　　　　　　　 a、b异号时对称轴在y轴右侧
　　　　　　　　　　　　 b＝０时对称轴是y轴c决定抛物线与y轴的交点：c＞０时抛物线交于y轴的正半轴
　　　　　　　　　　c＝０时抛物线过原点
　　　　　　　　　　c＜０时抛物线交于y轴的负半轴四、 a、b、c符号的确定1１、二次函数y=ax2+bx+c(a≠0)的图象如图所示，则a、b、c的符号为（　）
A、a>0,b=0,c>0 B、a<0,b>0,c<0
C、a>0,b=0,c<0 D、a<0,b=0,c<0CoC练习：1五、二次函数解析式的两种形式:已知顶点坐标、对称轴或最值已知任意三点坐标1 选择合适的方法求二次函数解析式： 1、抛物线经过（2，0）（0，-2）（-2，4）三点。2、抛物线的顶点坐标是（6，-2），且与
X轴的一个交点的横坐标是8。练 习1有两个交点有两个相异实数根b2-4ac > 0有一个交点有两个相等实数根b2-4ac = 0没有交点没有实数根b2-4ac < 0一元二次方程ax2+bx+c=0的根 就是
二次函数y=ax2+bx+c图象与x轴交点的横坐标六、二次函数与一元二次方程的关系1１、已知抛物线y＝x2－ m x＋m－１.(2)若抛物线与y轴交于正半轴，则m______；　　　　　　　　(1)若抛物线经过坐标系原点，则m______；　　　　　　　(3)若抛物线的对称轴为y轴，则m______。(4)若抛物线与x轴只有一个交点，则m_______. = 1 ＞1= 2= 0２、不论x为何值时，函数y=ax2+bx+c（a≠0）
　　的值永远为正的条件是____　　　　　__a>0,△<0练 习1B1.抛物线y=2x2+8x-11的顶点在 （ ）
A.第一象限 B.第二象限
C.第三象限 D.第四象限
2.不论k 取任何实数，抛物线y=a(x+k)2+k(a≠0)的
顶点都在A.直线y = x上 B.直线y = - x上
C.x轴上 D.y轴上
3.若二次函数y=ax2 + 4x+a-1的最小值是2,则a的值是
A、4 B. -1 C. 3 D.4或-1
4.若二次函数 y=ax2 + b x + c 的图象如下,与x
轴的一个交点为(1,0),则下列
各式中不成立的是( )
A.b2-4ac>0 B.abc>0
C.a+b+c=0 D.a-b+c<0CA B( )
（ ）　强化训练题15.若把抛物线y=x2+bx+c向左平移2个单位,再向上平
移3个单位,得抛物线y = x2 - 2x+1,则
A.b=2 B.b= - 6 , c= 6
C.b= - 8 D.b= - 8 , c= 18
6.若一次函数 y= ax + b 的图象经过第二、三、四象
限，则二次函数y = ax2 + bx - 3的大致图象是 ( )( )
B
-3-3-3-3C
17.在同一直角坐标系中,二次函数y=ax2+
bx+c与一次函数y=ax+c的大致图象可能是 （ ）
C
18、已知二次函数y=ax2+bx+c的图象如图所示，
下列结论：①a+b+c<0 ; ②a-b+c>0 ;
③abc>0 ; ④b=2a .其中正确的结论有（ ）A.4个 B.3个 C.2个 D.1个B
19、函数y=ax2-ax+3x+1的图象与x轴有且只有一个交点，那么a的值和交点坐标分别为 。9或110、已知二次函数y=a（x-h）2+k的图象过原点，最小值是-8，且形状与抛物线y=0.5x2-3x-5的形状相同，其解析式为 。y=0.5（x-16）2-811、若x为任意实数，则二次函数y=x2+2x+3的函数值y的取值范围是 。y≥2112、若抛物线y=ax2+2x+c的顶点坐标是（2，3），则a= ，c= 。-0.5113、抛物线y=2x2-4x-1是由抛物线y=2x2-bx+c向左平移1个单位，再向下平移2个单位得到的，则b= ，c= 。14、已知抛物线y=2x2+bx+8的顶点在x轴上，则b= 。83±8115、若二次函数y=（m-8）x2+2x+m2-64的图象过原点，则m= 。-816、如果点P（1，a）和点Q（-1，b）在抛物线y=-x2+1上，那么线段PQ的长为 。17、已知y=x2-（12-k）x+12，当x＞1时，y随x的增大而增大，当x＜1时，y随x的增大而减小，则k的值为 。210118、已知二次函数y=ax2+bx+c的图象经过点（1，-2），则a+b+c的值是 。19、直线y=-2x-3与抛物线y=x2+（3m+1）x+2m的对称轴交于点（-2，1），则m= 。-2120、抛物线y=-（x-m）（x-3-k）+m与抛物线y=（x-3）2+4关于原点对称，则m+k= 。21、已知二次函数的图象过（2，0），（6，0）两点，且顶点在直线y=0.75x上，求此二次函数的解析式。-9y=-0.75（x-4）2+31实际问题抽象转化数学问题运用数学知识问题的解返回解释检验二次函数的应用1结束寄语只有不断的思考,才会有新的发现;只有量的变化,才会有质的进步