锐角三角函数小结与复习

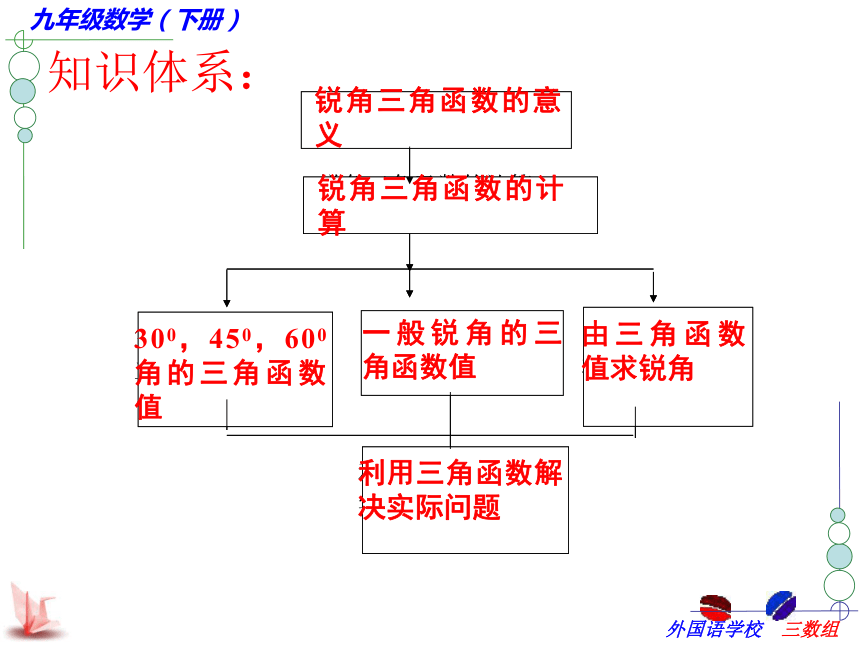
课件20张PPT。锐角三角函数小结与复习知识体系：复习提要: 1、了解锐角三角形函数的概念，能够正确地应用sinα、cosα、tanα、表示直角三角形中两边的比.
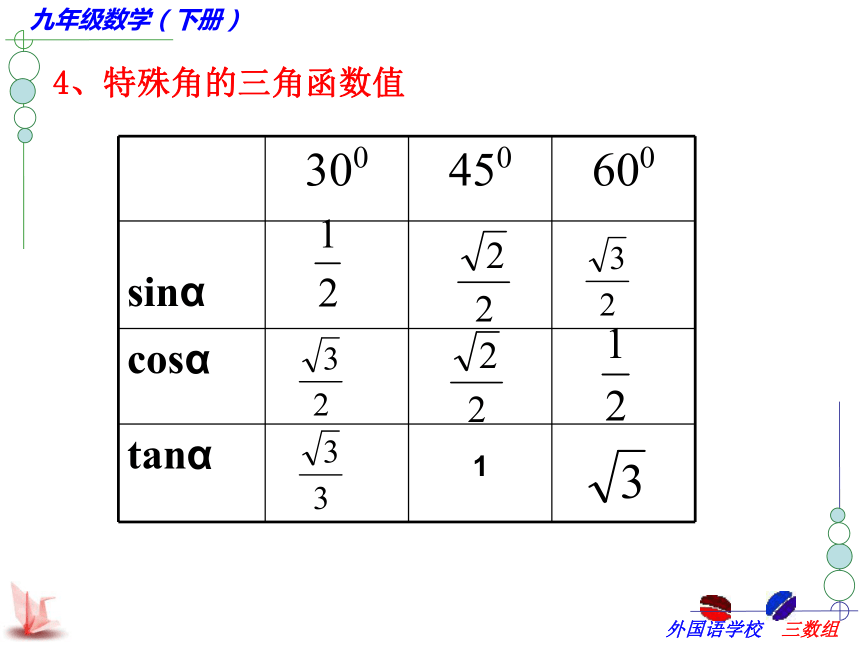
2、熟记30°，45°，60°角的三角函数值，会计算含有特殊角的三角函数式的值，会由一个特殊锐角的三角函数值，求出它对应的角度.
3、掌握直角三角形的边、角关系，会运用勾股定理、直角三角形的两个锐角互余及锐角三角形函数解直角三角形.
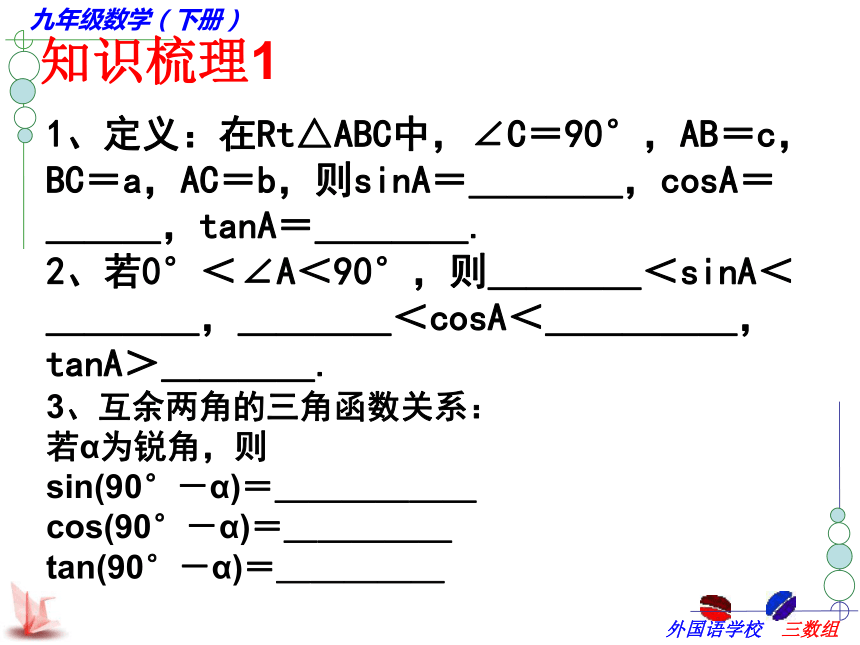
4、会用解直角三角形的有关知识解某些简单的实际问题.知识梳理11、定义：在Rt△ABC中，∠C＝90°，AB＝c，BC＝a，AC＝b，则sinA＝＿＿＿＿，cosA＝＿＿＿，tanA＝＿＿＿＿.
2、若0°＜∠A＜90°，则＿＿＿＿＜sinA＜＿＿＿＿，＿＿＿＿＜cosA＜＿＿＿＿＿，tanA＞＿＿＿＿.
3、互余两角的三角函数关系：
若α为锐角，则
sin(90°－α)＝＿＿＿＿＿＿
cos(90°－α)＝＿＿＿＿＿
tan(90°－α)＝＿＿＿＿＿4、特殊角的三角函数值
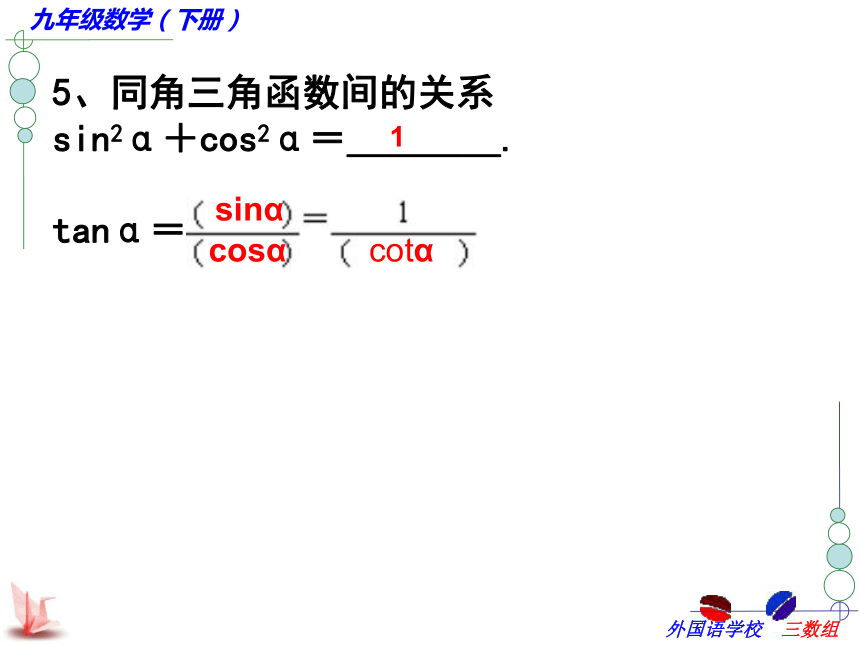
?15、同角三角函数间的关系
sin2α＋cos2α＝＿＿＿＿.
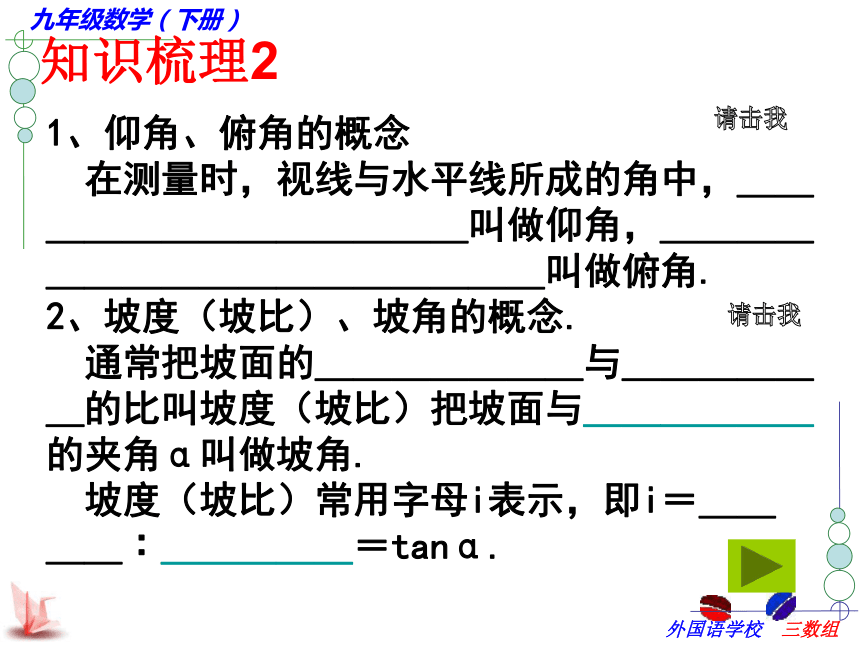
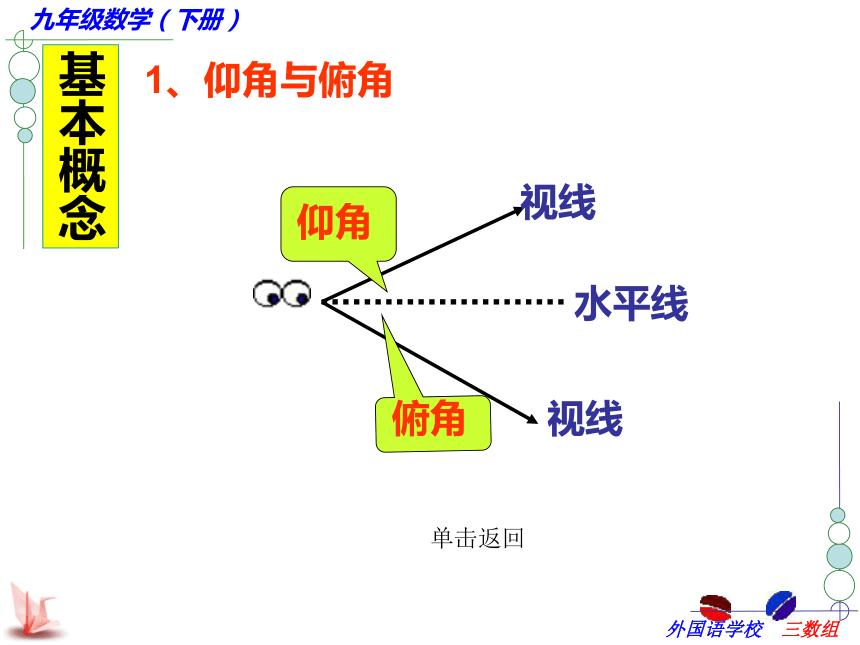
tanα＝1cotα知识梳理21、仰角、俯角的概念
在测量时，视线与水平线所成的角中，＿＿＿＿＿＿＿＿＿＿＿＿＿叫做仰角，＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿叫做俯角.
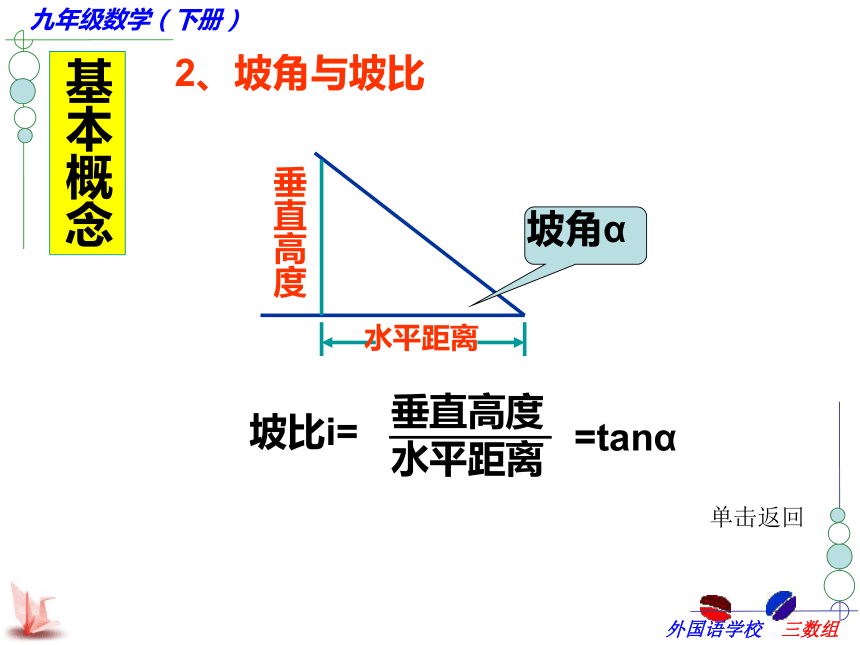
2、坡度（坡比）、坡角的概念.
通常把坡面的＿＿＿＿＿＿＿与＿＿＿＿＿＿的比叫坡度（坡比）把坡面与＿＿＿＿＿＿的夹角α叫做坡角.
坡度（坡比）常用字母i表示，即i＝＿＿＿＿∶＿＿＿＿＿＝tanα.请击我请击我基本概念视线视线水平线1、仰角与俯角单击返回基本概念2、坡角与坡比垂直高度=tanα单击返回基本概念3、方位角60 °北偏东60 °
45 °?南偏东45 °或东南方向基础训练一、填空题
1、在Rt△ABC中，∠C＝90°，AC＝4，BC＝3，则tanA＝＿＿＿＿＿，cosA＝＿＿＿＿.
2、在△ABC中，∠C＝90°，若tanA＝　，则sinA＝＿＿＿＿＿.
3、在平面直角坐标系中，已知点A（3,0）和点B（0,－4），则tan∠OAB＝＿＿＿＿＿.
4、α是正十二边形的中心角，则cosα＝＿＿＿＿＿.二、选择题
1、△ABC中，∠C＝90°，若sinA＝　 ，则tanA等于（　　）
2、在α是锐角，且sinα＝　，则cos(90°－α)等于（　　）
3、在△ABC中，∠C＝90°，tanA＝　，则tanB等于（　　）4、下列锐角三角函数值可能为　 的是（　　）
A、sinA B、sin2A
C、cosA D、tanA
5、已知α为锐角，下列结论：①sinα＋cosα＝1；②若α＞15°，则sinα＞cosα；③若cosα＞　，则α＜60°；④
有（　　）
A、1个 B、2个 C、3个 D、4个三、解答题
如图，在锐角△ABC中，AB＝c，BC＝a，AC＝b，∠C＝α，用式子表示△ABC的面积.问题研讨例1：如图，已知正方形ABCD的边长为2，如果将线段BD绕着点B旋转后，点D落在CB延长线上的D'处，那么tan∠BAD'等于（　　）例3、我们知道，“直角三角形斜边上的高线将三角形分成两个与原三角形相似的直角三角形”，用这一方法，将矩形ABCD分割成大小不同的七个相似直角三角形，按从大到小的顺序编号为①至⑦（如图），从而制成一副“三角七巧板”。 已知线段AB=1，∠BAC=θ
（1）请用θ的三角函数表示
线段BE的长________；
（2）图中与BE相等的线段
是__________；
（3）仔细观察图形，求出⑦
中最短的直角边DH的长（用θ
的三角函数表示）★例4：（2004镇江）如图，已知边长为5的等边△ABC纸片，点E在AC边上，点F在AB边上，沿着EF折叠，使点A落在BC边上的点D的位置且ED⊥BC，求CE的长.例5：如图，甲、乙两只捕捞船同时从A港出海捕鱼，甲船以每小时15　km的速度沿西偏北30°方向前进，乙船以每小时15km的速度沿东北方向前进.甲船航行2h到达C处，发现鱼具丢在乙船上，于是甲船快速（匀速）沿北偏东75°的方向追赶，结果两船在B处相遇.（1）甲船从C处追赶上乙船用了多少时间？
（2）甲船追赶乙船的速度是多少？例6、如图所示，A、B两个村庄，AB，BC，CD为公路，BD为田地，AD为河宽，且CD与AD互相垂直，现在要从点E处开始铺设通往村庄A、村庄B的一条电缆，共有如下两种铺设方案：FF规律总结 1、已知三角函数值或者要求三角函数值时，先找Rt△或构造Rt△.
2、解决折叠问题的关键是找到能完全重合的三角形.