2024年中考数学专项分类复习提升检测卷—不等式与不等式组(含答案)
文档属性
| 名称 | 2024年中考数学专项分类复习提升检测卷—不等式与不等式组(含答案) | 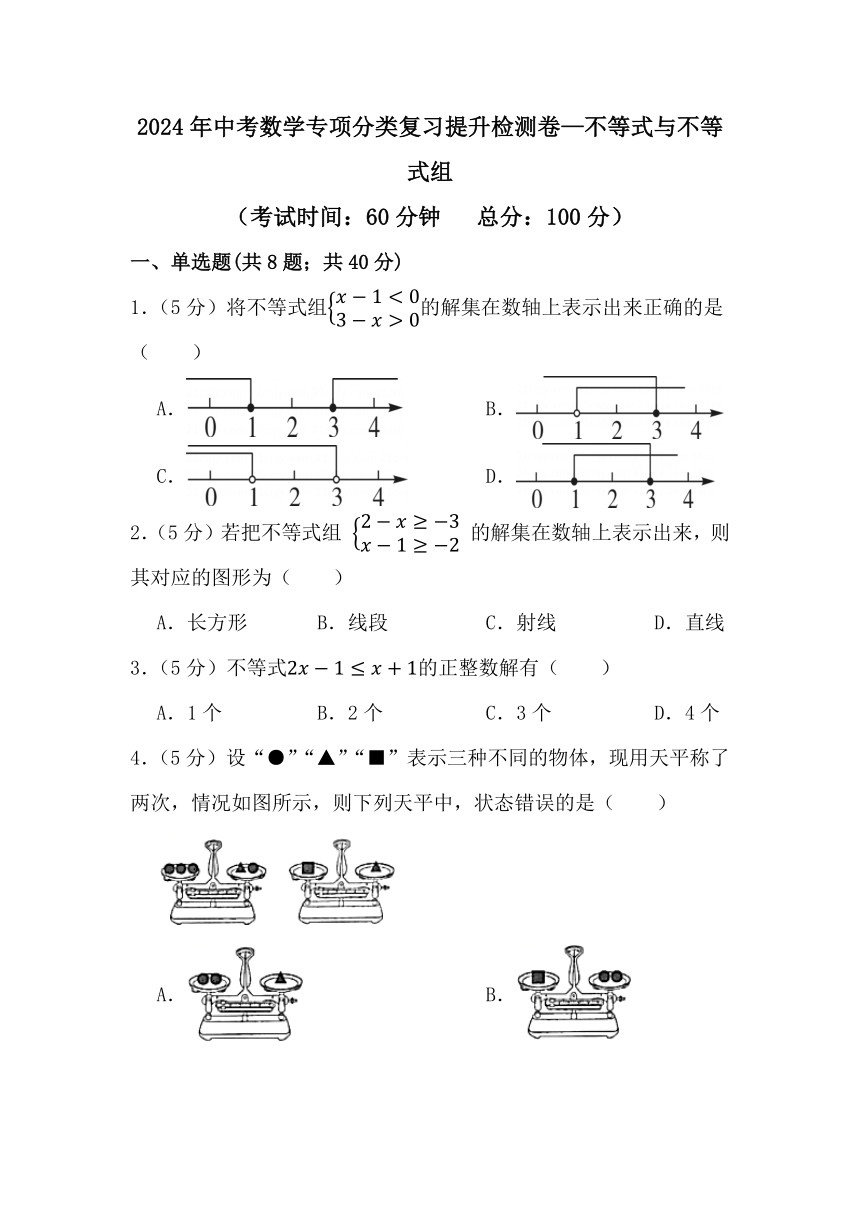 | |
| 格式 | docx | ||
| 文件大小 | 154.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-18 11:15:42 | ||
图片预览



文档简介
2024年中考数学专项分类复习提升检测卷—不等式与不等式组
(考试时间:60分钟 总分:100分)
单选题(共8题;共40分)
1.(5分)将不等式组的解集在数轴上表示出来正确的是( )
A. B.
C. D.
2.(5分)若把不等式组 的解集在数轴上表示出来,则其对应的图形为( )
A.长方形 B.线段 C.射线 D.直线
3.(5分)不等式的正整数解有( )
A.1个 B.2个 C.3个 D.4个
4.(5分)设“●”“▲”“■”表示三种不同的物体,现用天平称了两次,情况如图所示,则下列天平中,状态错误的是( )
A. B.
C. D.
5.(5分)若,则下列不等式不一定成立的是( )
A. B.
C. D.
6.(5分)不等式x+1>2x﹣4的解集是( )
A.x<5 B.x>5 C.x<1 D.x>1
7.(5分)苏州市2018年2月1日的气温是t℃,这天的最高气温是5℃,最低气温是-2℃,则当天我市气温t(℃)变化范围是( )
A.
B.
C.
D.
8.(5分)不等式组有4个整数解,则m的取值范围是( )
A. B.
C. D.
填空题(共5题;共15分)
9.(3分)如果不等式组有解,那么m的取值范围是 .
10.(3分)如图所示,运行程序规定:从“输入一个值x”到“结果是否大于79”为一次程序操作,如果程序操作进行了三次才停止,那么x的取值范围是 .
11.(3分)对于有理数 ,我们规定 表示不大于 的最大整数,例如: , , ,若 ,则整数x的取值是 .
12.(3分)某校计划组织师生乘坐大小两种客车去参加一次大型公益活动,每辆大客车的乘客座位数是35个,每辆小客车的乘客座位数是18个,这样租用6辆大客车和5辆小客车恰好全部坐满.由于最后参加活动的人数增加了30人,在保持租用车辆总数不变的情况下,学校决定调整租车方案,以确保乘载全部参加活动的师生,则该校最后所租用小客车数量的最大值为 辆.
13.(3分)若方程组 的解x、y满足 ,则a的取值范围为 .
三、解答题(共3题;共45分)
14.(15分)某店主购进,两种礼盒.已知,两种礼盒的单价比为2∶3,单价和为10元.该店主进种礼盒的数量是种礼盒数量的2倍少1个,且这两种礼盒花费不超过398元,则种礼盒最多购买多少个?
15.(15分)不等式组 请按下列步骤完成解答:
(1)(3分)解不等式①,得 ;
(2)(3分)解不等式②,得 ;
(3)(5分)把不等式①和②的解集在数轴上表示出来;
(4)(4分)原不等式组的解集为
16.(15分)某校20名同学去工厂进行暑假实践活动,每名同学每天可以加工甲种零件5个或乙种零件4个,已知每加工一个甲种零件可获利16元,每加工一个乙种零件可获利24元,若要使车间每天获利不低于1800元,加工乙种零件的同学至少有多少名?
答案
1.【答案】C
2.【答案】B
3.【答案】B
4.【答案】D
5.【答案】C
6.【答案】A
7.【答案】D
8.【答案】D
9.【答案】
10.【答案】
11.【答案】-17,-16,-15
12.【答案】3
13.【答案】a>-4
14.【答案】解:∵,两种礼盒的单价比为2∶3,单价和为10元
∴A礼盒的单价为元,礼盒的单价为6元,
设购买A礼盒个,则B礼盒个,根据题意可得:
解得:;
为正整数,
最多为25,
答:种礼盒最多购买25个.
15.【答案】(1)
(2)
(3)
(4) .
16.【答案】解:设加工乙种零件的同学x人,则加工甲种零件的同学有人.
根据题意得,
解之得,
因为x是正整数,所以x最小值是13,
答:加工乙种零件的同学至少有13人
(考试时间:60分钟 总分:100分)
单选题(共8题;共40分)
1.(5分)将不等式组的解集在数轴上表示出来正确的是( )
A. B.
C. D.
2.(5分)若把不等式组 的解集在数轴上表示出来,则其对应的图形为( )
A.长方形 B.线段 C.射线 D.直线
3.(5分)不等式的正整数解有( )
A.1个 B.2个 C.3个 D.4个
4.(5分)设“●”“▲”“■”表示三种不同的物体,现用天平称了两次,情况如图所示,则下列天平中,状态错误的是( )
A. B.
C. D.
5.(5分)若,则下列不等式不一定成立的是( )
A. B.
C. D.
6.(5分)不等式x+1>2x﹣4的解集是( )
A.x<5 B.x>5 C.x<1 D.x>1
7.(5分)苏州市2018年2月1日的气温是t℃,这天的最高气温是5℃,最低气温是-2℃,则当天我市气温t(℃)变化范围是( )
A.
B.
C.
D.
8.(5分)不等式组有4个整数解,则m的取值范围是( )
A. B.
C. D.
填空题(共5题;共15分)
9.(3分)如果不等式组有解,那么m的取值范围是 .
10.(3分)如图所示,运行程序规定:从“输入一个值x”到“结果是否大于79”为一次程序操作,如果程序操作进行了三次才停止,那么x的取值范围是 .
11.(3分)对于有理数 ,我们规定 表示不大于 的最大整数,例如: , , ,若 ,则整数x的取值是 .
12.(3分)某校计划组织师生乘坐大小两种客车去参加一次大型公益活动,每辆大客车的乘客座位数是35个,每辆小客车的乘客座位数是18个,这样租用6辆大客车和5辆小客车恰好全部坐满.由于最后参加活动的人数增加了30人,在保持租用车辆总数不变的情况下,学校决定调整租车方案,以确保乘载全部参加活动的师生,则该校最后所租用小客车数量的最大值为 辆.
13.(3分)若方程组 的解x、y满足 ,则a的取值范围为 .
三、解答题(共3题;共45分)
14.(15分)某店主购进,两种礼盒.已知,两种礼盒的单价比为2∶3,单价和为10元.该店主进种礼盒的数量是种礼盒数量的2倍少1个,且这两种礼盒花费不超过398元,则种礼盒最多购买多少个?
15.(15分)不等式组 请按下列步骤完成解答:
(1)(3分)解不等式①,得 ;
(2)(3分)解不等式②,得 ;
(3)(5分)把不等式①和②的解集在数轴上表示出来;
(4)(4分)原不等式组的解集为
16.(15分)某校20名同学去工厂进行暑假实践活动,每名同学每天可以加工甲种零件5个或乙种零件4个,已知每加工一个甲种零件可获利16元,每加工一个乙种零件可获利24元,若要使车间每天获利不低于1800元,加工乙种零件的同学至少有多少名?
答案
1.【答案】C
2.【答案】B
3.【答案】B
4.【答案】D
5.【答案】C
6.【答案】A
7.【答案】D
8.【答案】D
9.【答案】
10.【答案】
11.【答案】-17,-16,-15
12.【答案】3
13.【答案】a>-4
14.【答案】解:∵,两种礼盒的单价比为2∶3,单价和为10元
∴A礼盒的单价为元,礼盒的单价为6元,
设购买A礼盒个,则B礼盒个,根据题意可得:
解得:;
为正整数,
最多为25,
答:种礼盒最多购买25个.
15.【答案】(1)
(2)
(3)
(4) .
16.【答案】解:设加工乙种零件的同学x人,则加工甲种零件的同学有人.
根据题意得,
解之得,
因为x是正整数,所以x最小值是13,
答:加工乙种零件的同学至少有13人
同课章节目录
