2024年四川省成都市九年级中考数学B卷专项强化训练十三 (含答案解析)
文档属性
| 名称 | 2024年四川省成都市九年级中考数学B卷专项强化训练十三 (含答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 180.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-18 11:03:36 | ||
图片预览


文档简介
2024成都中考B卷专项强化训练十三
班级:________ 姓名:________ 得分:________
(满分:50分)
一、填空题(本大题共5个小题,每小题4分,共20分)
19. 若=2.236,则=________.(精确到0.01)
20. 已知关于x的方程kx2-2x+1=0有两个不相等的实数根,则k的最大整数值是________.
21. 现有4张卡片,正面分别书写的是“冰化成水”“酒精燃烧”“铁棒成针”“牛奶变酸”四种不同的变化,它们除卡片上的字不同之外完全相同,把这4张卡片背面朝上洗匀,从中随机抽取两张,则这两张卡片呈现的变化都是物理变化的概率是________.
22. 对于平面直角坐标系xOy中的点P和⊙O,给出如下的定义:若⊙O上存在两点A,B,使得∠APB=90°,则称点P为⊙O的“关联点”.已知点D(,),E(0,-),F(2,0).当⊙O的半径为1时,在点D,E,F中,⊙O的“关联点”是________.
23. 如图,在菱形ABCD中,∠ABC=60°,AB=4,动点E从点B出发沿BA以1个单位/秒的速度向点A运动,同时,动点F从点B出发,以相同的速度沿AB的延长线运动,当点E到达点A时,它们同时停止运动,CE与DF交于点G.设点E的运动时间为t秒,则当t=________秒时,DG=DC;当点E运动到点A时,点G运动路径长为________.
第23题图
二、解答题(本大题共3个小题,共30分)
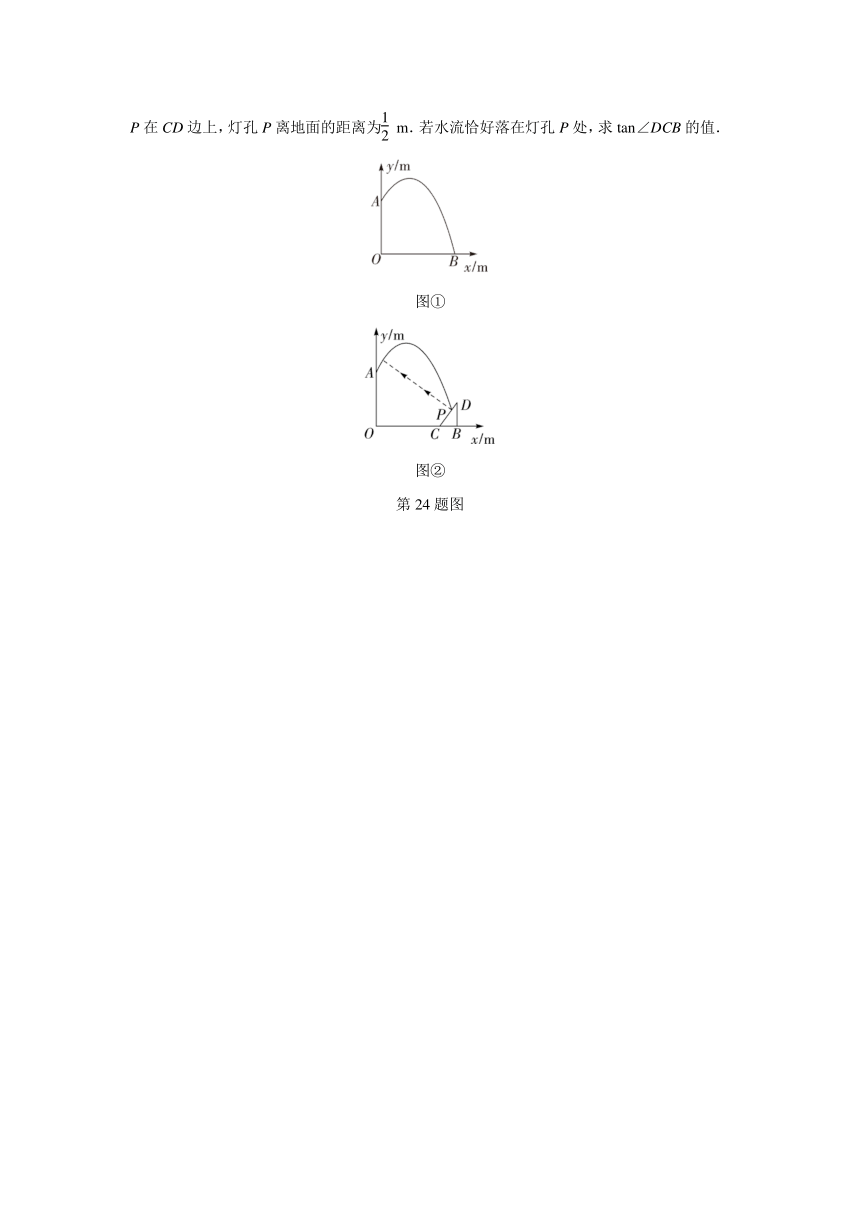
24. (本小题满分8分)如图①,一个圆形喷水池的中央竖直安装了一个柱形喷水装置OA,A处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下,按如图所示的平面直角坐标系,水流喷出的高度y(m)与水平距离x(m)之间的关系式是y=-x2+2x+(x≥0).
(1)柱子OA的高度是多少米?若不计其他因素,水池的半径至少为多少米时,才能使喷出的水流不至于落在水池外?
(2)如图②,为了吸引更多的游客前来参观游玩,准备在水池的边缘增设彩光灯,彩光灯的底座为Rt△BCD ,其中BC边在地面上,点C离柱子的距离为2.1 m,∠CBD=90°,灯孔P在CD边上,灯孔P离地面的距离为 m.若水流恰好落在灯孔P处,求tan∠DCB的值.
图①
图②
第24题图
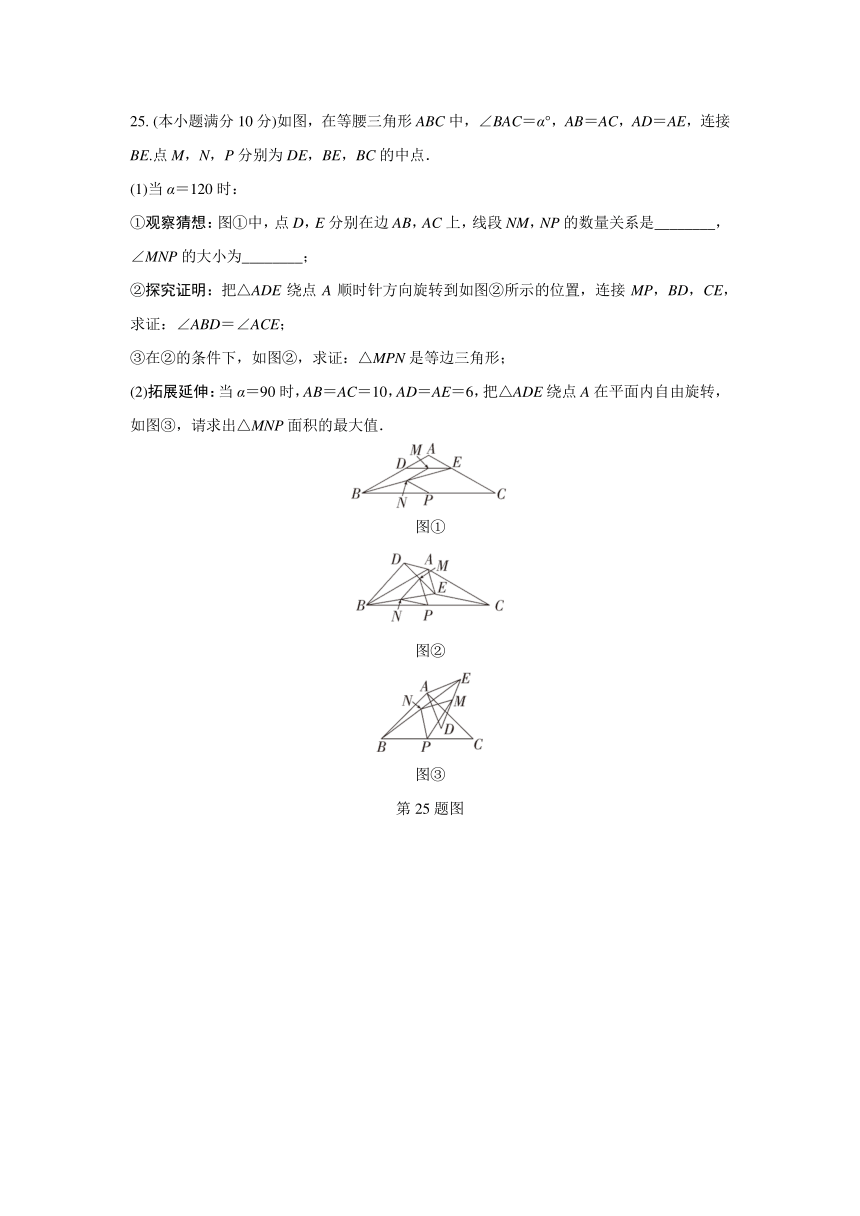
25. (本小题满分10分)如图,在等腰三角形ABC中,∠BAC=α°,AB=AC,AD=AE,连接BE.点M,N,P分别为DE,BE,BC的中点.
(1)当α=120时:
①观察猜想:图①中,点D,E分别在边AB,AC上,线段NM,NP的数量关系是________,∠MNP的大小为________;
②探究证明:把△ADE绕点A顺时针方向旋转到如图②所示的位置,连接MP,BD,CE,求证:∠ABD=∠ACE;
③在②的条件下,如图②,求证:△MPN是等边三角形;
(2)拓展延伸:当α=90时,AB=AC=10,AD=AE=6,把△ADE绕点A在平面内自由旋转,如图③,请求出△MNP面积的最大值.
图①
图②
图③
第25题图
26. (本小题满分12分)如图,Rt△ABO的两直角边OA,OB分别在x轴的负半轴和y轴的正半轴上,O为坐标原点,A,B两点的坐标分别为(-3,0),(0,4),抛物线y=x2+bx+c经过点B,且顶点在直线x=上.
(1)求抛物线对应的函数表达式;
(2)若△DCE是由△ABO沿x轴向右平移得到的,当四边形ABCD是菱形时,试判断点C和点D是否在该抛物线上,并说明理由;
(3)在(2)的条件下,若点F与点D关于y轴对称,过点F作直线GF交抛物线于点H,M.点H在点M左侧,连接GD,DM,HD.设直线GF的表达式为y=kx+b,是否存在实数k,使得△GHD与△DGM相似?若存在,请求出k值以及△DHM的面积;若不存在,请说明理由.
第26题图
参考答案与解析
19. 4.47 【解析】==2,∵=2.236,∴=2=2×2.236=4.472≈4.47.
20. -1 【解析】∵关于x的方程kx2-2x+1=0有两个不相等的实数根,∴Δ>0且k≠0,即Δ=(-2)2-4k>0且k≠0,∴k<1且k≠0,∴k的最大整数值为-1.
21. 【解析】把4张卡片“冰化成水”“酒精燃烧”“铁棒成针”“牛奶变酸”依次记为A,B,C,D,其中物理变化为A,C,画树状图如解图,共有12种等可能的结果,其中两张卡片呈现的变化都是物理变化的结果有2种,即AC,CA,∴从中随机抽取两张,两张卡片呈现的变化都是物理变化的概率是=.
第21题解图
22. 点D,E 【解析】如解图,过点E作⊙O的切线,设切点为R,∵⊙O的半径为1,∴RO=1.∵EO=,∴∠OER=45°,根据切线长定理得出⊙O的左侧还有一个切点,使得组成的角等于45°,∴点E是⊙O的“关联点”.∵D(,),E(0,-),F(2,0),∴OF>EO,在⊙O上不可能找到两点与点F的连线的夹角等于90°,∴点F不是⊙O的“关联点”.∵DO<EO,在⊙O上能找到两点与点D的连线的夹角等于90°,∴点D一定是⊙O的“关联点”,∴在点D,E,F中,⊙O的“关联点”是点D,E.
第22题解图
23. ; 【解析】当DG=DC时,如解图①,过点D作DH⊥AF,交FA的延长线于点H,由题意可得BE=BF=t.∵四边形ABCD是菱形,∴AB∥CD,∴△EFG∽△CDG,∴=,∴=,∴FG=2t.在Rt△ADH中,∵∠DAH=∠ABC=60°,∴∠ADH=30°,∴AH=AD=2,DH=2.在Rt△FDH中,由勾股定理得DH2+HF2=DF2,即(2)2+(6+t)2=(4+2t)2,解得t=或t=-4(舍去),∴当t=时,DG=DC;如解图①,连接BG并延长交CD于点M,∵AB∥CD,∴==,∴=,∴CM=2,∴直线BG始终经过定点M,点G的运动路径为一条线段.由题意可得,当点E到达点A时点G的运动路径长最大,如解图②,过点G作GN⊥AB于点N,连接BG.∵AB∥CD,∴==,∴AG=AC.∵四边形ABCD是菱形,∠ABC=60°,∴△ABC是等边三角形,∴AC=AB=4,∴AG=.在Rt△AGN中,AN=AG=,GN=,在Rt△BGN中,BN=AB-AN=,∴BG==,∴点G运动路径长为.
图①
图②
第23题解图
24. 解:(1)∵当x=0时,y=,
∴柱子OA的高度为 m;
在y=-x2+2x+中,当y=0时,即-x2+2x+=0,
解得x1=+1,x2=1-.
又∵x≥0,
∴x=+1,
∴水池的半径至少为(+1)m时才能使喷出的水流不至于落在水池外;
(2)根据题意,当y=时,
即-x2+2x+=,
解得x1=,x2=-(舍去),
∴tan ∠DCB==.
25. (1)解:①NM=NP,60°;
【解法提示】∵AB=AC,AD=AE,∴BD=CE.∵点M,N,P分别为DE,BE,BC的中点,∴MN是△BED的中位线,PN是△BCE的中位线,∴MN=BD,PN=CE,MN∥AB,PN∥AC,∴MN=PN,∠ENM=∠EBA,∠ENP=∠AEB,∴∠ENM+∠ENP=∠EBA+∠AEB.∵∠ABE+∠AEB=180°-∠BAE=180°-120°=60°,∴∠MNP=60°.
②证明:由旋转的性质得∠BAD=∠CAE.
∵AB=AC,AD=AE,
∴△ABD≌△ACE(SAS),
∴∠ABD=∠ACE;
③证明:∵△ABD≌△ACE,
∴BD=CE.
∵点M,N,P分别为DE,BE,BC的中点,
∴MN是△BED的中位线,PN是△BCE的中位线,
∴MN=BD,PN=CE,MN∥BD,PN∥CE,
∴MN=PN,∠ENM=∠EBD,∠BPN=∠BCE,
∴∠ENP=∠NBP+∠BPN=∠NBP+∠BCE.
∵∠EBD=∠ABD+∠ABE=∠ACE+∠ABE,
∴∠MNP=∠ENM+∠ENP=∠ACE+∠ABE+∠NBP+∠BCE=180°-∠BAC=180°-120°=60°,
∴△MPN是等边三角形;
(2)解:如解图,连接BD,由题意得:BD≤AB+AD,即BD≤16,
同(1)得MN=BD,MN=PN,∠MNP=90°,
∴MN≤8,△MNP是等腰直角三角形,
∴S△MNP=MN2,
∴当MN=8时,S△MNP最大,
此时,S△MNP=MN2=×82=32,
∴△MNP面积的最大值为32.
第25题解图
26. 解:(1)∵y=x2+bx+c的顶点在直线x=上,
∴可设所求抛物线对应的函数表达式为y=(x-)2+m.
∵点B(0,4)在该抛物线上,
∴4=(0-)2+m,
解得m=-,
∴抛物线对应的函数表达式为y=(x-)2-=x2-x+4;
(2)点C和点D在该抛物线上.理由如下:
在Rt△ABO中,OA=3,OB=4,
∴AB=5.
∵四边形ABCD是菱形,
∴BC=CD=DA=AB=5.
∵A,B两点的坐标分别为(-3,0),(0,4),
∴C,D两点的坐标分别是(5,4),(2,0),
当x=5时,y=×52-×5+4=4;
当x=2时,y=×22-×2+4=0,
∴点C和点D在该抛物线上;
(3)存在,k=.理由如下:
∵D(2,0),由对称得F(-2,0),
设直线GF的表达式为y=kx+b,
代入点F,得-2k+b=0,即b=2k,
∴G(0,2k);
当直线与抛物线相交时,设H(x1,y1),M(x2,y2),
则H(x1,kx1+2k),M(x2,kx2+2k),
令x2-x+4=kx+2k,
整理得,2x2-(10+3k)x+12-6k=0,①
∴Δ=(10+3k)2-8(12-6k)>0,
解得x<-6-或x>-6.
∵x1,x2是方程①的解,∴由根与系数的关系,得x1+x2=,x1x2=6-3k.
当△GHD与△DGM相似时,分两种情况讨论.
①△GHD∽△GMD,则点H,M重合,不符合题意;
②△GHD∽△GDM,则GD2=GH·GM,
∵G(0,2k),D(2,0),H(x1,kx1+2k),M(x2,kx2+2k),
∴4+4k2=·,
整理,得4(1+k2)=(1+k2)x1x2,
∴6-3k=4,
解得k=.
当k=时,方程①可变形为2x2-12x+8=0,
解得x1=3-,x2=3+,
∴y2-y1=k(x2-x1)=×2= ,
∴S△HDM=S△FDM-S△FDH=×4×(y2-y1)=.
即当k=时,△GHD与△DGM相似.此时△DHM的面积为.
班级:________ 姓名:________ 得分:________
(满分:50分)
一、填空题(本大题共5个小题,每小题4分,共20分)
19. 若=2.236,则=________.(精确到0.01)
20. 已知关于x的方程kx2-2x+1=0有两个不相等的实数根,则k的最大整数值是________.
21. 现有4张卡片,正面分别书写的是“冰化成水”“酒精燃烧”“铁棒成针”“牛奶变酸”四种不同的变化,它们除卡片上的字不同之外完全相同,把这4张卡片背面朝上洗匀,从中随机抽取两张,则这两张卡片呈现的变化都是物理变化的概率是________.
22. 对于平面直角坐标系xOy中的点P和⊙O,给出如下的定义:若⊙O上存在两点A,B,使得∠APB=90°,则称点P为⊙O的“关联点”.已知点D(,),E(0,-),F(2,0).当⊙O的半径为1时,在点D,E,F中,⊙O的“关联点”是________.
23. 如图,在菱形ABCD中,∠ABC=60°,AB=4,动点E从点B出发沿BA以1个单位/秒的速度向点A运动,同时,动点F从点B出发,以相同的速度沿AB的延长线运动,当点E到达点A时,它们同时停止运动,CE与DF交于点G.设点E的运动时间为t秒,则当t=________秒时,DG=DC;当点E运动到点A时,点G运动路径长为________.
第23题图
二、解答题(本大题共3个小题,共30分)
24. (本小题满分8分)如图①,一个圆形喷水池的中央竖直安装了一个柱形喷水装置OA,A处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下,按如图所示的平面直角坐标系,水流喷出的高度y(m)与水平距离x(m)之间的关系式是y=-x2+2x+(x≥0).
(1)柱子OA的高度是多少米?若不计其他因素,水池的半径至少为多少米时,才能使喷出的水流不至于落在水池外?
(2)如图②,为了吸引更多的游客前来参观游玩,准备在水池的边缘增设彩光灯,彩光灯的底座为Rt△BCD ,其中BC边在地面上,点C离柱子的距离为2.1 m,∠CBD=90°,灯孔P在CD边上,灯孔P离地面的距离为 m.若水流恰好落在灯孔P处,求tan∠DCB的值.
图①
图②
第24题图
25. (本小题满分10分)如图,在等腰三角形ABC中,∠BAC=α°,AB=AC,AD=AE,连接BE.点M,N,P分别为DE,BE,BC的中点.
(1)当α=120时:
①观察猜想:图①中,点D,E分别在边AB,AC上,线段NM,NP的数量关系是________,∠MNP的大小为________;
②探究证明:把△ADE绕点A顺时针方向旋转到如图②所示的位置,连接MP,BD,CE,求证:∠ABD=∠ACE;
③在②的条件下,如图②,求证:△MPN是等边三角形;
(2)拓展延伸:当α=90时,AB=AC=10,AD=AE=6,把△ADE绕点A在平面内自由旋转,如图③,请求出△MNP面积的最大值.
图①
图②
图③
第25题图
26. (本小题满分12分)如图,Rt△ABO的两直角边OA,OB分别在x轴的负半轴和y轴的正半轴上,O为坐标原点,A,B两点的坐标分别为(-3,0),(0,4),抛物线y=x2+bx+c经过点B,且顶点在直线x=上.
(1)求抛物线对应的函数表达式;
(2)若△DCE是由△ABO沿x轴向右平移得到的,当四边形ABCD是菱形时,试判断点C和点D是否在该抛物线上,并说明理由;
(3)在(2)的条件下,若点F与点D关于y轴对称,过点F作直线GF交抛物线于点H,M.点H在点M左侧,连接GD,DM,HD.设直线GF的表达式为y=kx+b,是否存在实数k,使得△GHD与△DGM相似?若存在,请求出k值以及△DHM的面积;若不存在,请说明理由.
第26题图
参考答案与解析
19. 4.47 【解析】==2,∵=2.236,∴=2=2×2.236=4.472≈4.47.
20. -1 【解析】∵关于x的方程kx2-2x+1=0有两个不相等的实数根,∴Δ>0且k≠0,即Δ=(-2)2-4k>0且k≠0,∴k<1且k≠0,∴k的最大整数值为-1.
21. 【解析】把4张卡片“冰化成水”“酒精燃烧”“铁棒成针”“牛奶变酸”依次记为A,B,C,D,其中物理变化为A,C,画树状图如解图,共有12种等可能的结果,其中两张卡片呈现的变化都是物理变化的结果有2种,即AC,CA,∴从中随机抽取两张,两张卡片呈现的变化都是物理变化的概率是=.
第21题解图
22. 点D,E 【解析】如解图,过点E作⊙O的切线,设切点为R,∵⊙O的半径为1,∴RO=1.∵EO=,∴∠OER=45°,根据切线长定理得出⊙O的左侧还有一个切点,使得组成的角等于45°,∴点E是⊙O的“关联点”.∵D(,),E(0,-),F(2,0),∴OF>EO,在⊙O上不可能找到两点与点F的连线的夹角等于90°,∴点F不是⊙O的“关联点”.∵DO<EO,在⊙O上能找到两点与点D的连线的夹角等于90°,∴点D一定是⊙O的“关联点”,∴在点D,E,F中,⊙O的“关联点”是点D,E.
第22题解图
23. ; 【解析】当DG=DC时,如解图①,过点D作DH⊥AF,交FA的延长线于点H,由题意可得BE=BF=t.∵四边形ABCD是菱形,∴AB∥CD,∴△EFG∽△CDG,∴=,∴=,∴FG=2t.在Rt△ADH中,∵∠DAH=∠ABC=60°,∴∠ADH=30°,∴AH=AD=2,DH=2.在Rt△FDH中,由勾股定理得DH2+HF2=DF2,即(2)2+(6+t)2=(4+2t)2,解得t=或t=-4(舍去),∴当t=时,DG=DC;如解图①,连接BG并延长交CD于点M,∵AB∥CD,∴==,∴=,∴CM=2,∴直线BG始终经过定点M,点G的运动路径为一条线段.由题意可得,当点E到达点A时点G的运动路径长最大,如解图②,过点G作GN⊥AB于点N,连接BG.∵AB∥CD,∴==,∴AG=AC.∵四边形ABCD是菱形,∠ABC=60°,∴△ABC是等边三角形,∴AC=AB=4,∴AG=.在Rt△AGN中,AN=AG=,GN=,在Rt△BGN中,BN=AB-AN=,∴BG==,∴点G运动路径长为.
图①
图②
第23题解图
24. 解:(1)∵当x=0时,y=,
∴柱子OA的高度为 m;
在y=-x2+2x+中,当y=0时,即-x2+2x+=0,
解得x1=+1,x2=1-.
又∵x≥0,
∴x=+1,
∴水池的半径至少为(+1)m时才能使喷出的水流不至于落在水池外;
(2)根据题意,当y=时,
即-x2+2x+=,
解得x1=,x2=-(舍去),
∴tan ∠DCB==.
25. (1)解:①NM=NP,60°;
【解法提示】∵AB=AC,AD=AE,∴BD=CE.∵点M,N,P分别为DE,BE,BC的中点,∴MN是△BED的中位线,PN是△BCE的中位线,∴MN=BD,PN=CE,MN∥AB,PN∥AC,∴MN=PN,∠ENM=∠EBA,∠ENP=∠AEB,∴∠ENM+∠ENP=∠EBA+∠AEB.∵∠ABE+∠AEB=180°-∠BAE=180°-120°=60°,∴∠MNP=60°.
②证明:由旋转的性质得∠BAD=∠CAE.
∵AB=AC,AD=AE,
∴△ABD≌△ACE(SAS),
∴∠ABD=∠ACE;
③证明:∵△ABD≌△ACE,
∴BD=CE.
∵点M,N,P分别为DE,BE,BC的中点,
∴MN是△BED的中位线,PN是△BCE的中位线,
∴MN=BD,PN=CE,MN∥BD,PN∥CE,
∴MN=PN,∠ENM=∠EBD,∠BPN=∠BCE,
∴∠ENP=∠NBP+∠BPN=∠NBP+∠BCE.
∵∠EBD=∠ABD+∠ABE=∠ACE+∠ABE,
∴∠MNP=∠ENM+∠ENP=∠ACE+∠ABE+∠NBP+∠BCE=180°-∠BAC=180°-120°=60°,
∴△MPN是等边三角形;
(2)解:如解图,连接BD,由题意得:BD≤AB+AD,即BD≤16,
同(1)得MN=BD,MN=PN,∠MNP=90°,
∴MN≤8,△MNP是等腰直角三角形,
∴S△MNP=MN2,
∴当MN=8时,S△MNP最大,
此时,S△MNP=MN2=×82=32,
∴△MNP面积的最大值为32.
第25题解图
26. 解:(1)∵y=x2+bx+c的顶点在直线x=上,
∴可设所求抛物线对应的函数表达式为y=(x-)2+m.
∵点B(0,4)在该抛物线上,
∴4=(0-)2+m,
解得m=-,
∴抛物线对应的函数表达式为y=(x-)2-=x2-x+4;
(2)点C和点D在该抛物线上.理由如下:
在Rt△ABO中,OA=3,OB=4,
∴AB=5.
∵四边形ABCD是菱形,
∴BC=CD=DA=AB=5.
∵A,B两点的坐标分别为(-3,0),(0,4),
∴C,D两点的坐标分别是(5,4),(2,0),
当x=5时,y=×52-×5+4=4;
当x=2时,y=×22-×2+4=0,
∴点C和点D在该抛物线上;
(3)存在,k=.理由如下:
∵D(2,0),由对称得F(-2,0),
设直线GF的表达式为y=kx+b,
代入点F,得-2k+b=0,即b=2k,
∴G(0,2k);
当直线与抛物线相交时,设H(x1,y1),M(x2,y2),
则H(x1,kx1+2k),M(x2,kx2+2k),
令x2-x+4=kx+2k,
整理得,2x2-(10+3k)x+12-6k=0,①
∴Δ=(10+3k)2-8(12-6k)>0,
解得x<-6-或x>-6.
∵x1,x2是方程①的解,∴由根与系数的关系,得x1+x2=,x1x2=6-3k.
当△GHD与△DGM相似时,分两种情况讨论.
①△GHD∽△GMD,则点H,M重合,不符合题意;
②△GHD∽△GDM,则GD2=GH·GM,
∵G(0,2k),D(2,0),H(x1,kx1+2k),M(x2,kx2+2k),
∴4+4k2=·,
整理,得4(1+k2)=(1+k2)x1x2,
∴6-3k=4,
解得k=.
当k=时,方程①可变形为2x2-12x+8=0,
解得x1=3-,x2=3+,
∴y2-y1=k(x2-x1)=×2= ,
∴S△HDM=S△FDM-S△FDH=×4×(y2-y1)=.
即当k=时,△GHD与△DGM相似.此时△DHM的面积为.
同课章节目录
