2023~2024学年沪科版九年级上册期末数学复习押题卷 (1)(含答案解析)
文档属性
| 名称 | 2023~2024学年沪科版九年级上册期末数学复习押题卷 (1)(含答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 244.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-18 12:08:33 | ||
图片预览


文档简介
2023-2024学年沪科版九年级上册期末数学复习押题卷
一、选择题
1.下列图形中,轴对称图形的个数是( )
A.1个 B.2个 C.3个 D.4个
2.如图,AD∥BE∥CF,AB=3,BC=6,DE=2,则EF的值为( )
A.2 B.3 C.4 D.5
3.如图, , 与 , 分别相交于点 , , ,与 的平分线 相交于点 ,且 ,则 的度数( )
A.70° B.65° C.60° D.55°
4.若,两点均在函数的图象上,且,则与的大小关系为( )
A. B. C. D.无法判断
5.如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,则下列结论不正确的是( )
A. B. C. D.
6.如图,在九年级体育测试中,小朱掷出的实心球的飞行高度y(米)与水平距离x(米)之间的关系大致满足二次函数,则小朱本次投掷实心球的成绩为( )
A.7m B.7.5m C.8m D.8.5m
7.抛物线y=(x﹣1)2+2与y轴交点坐标为( )
A.(0,1) B.(0,2) C.(1,2) D.(0,3)
8.已知点A在函数y1=﹣ (x>0)的图象上,点B在直线y2=kx+1+k(k为常数,且k≥0)上.若A,B两点关于原点对称,则称点A,B为函数y1,y2图象上的一对“友好点”.请问这两个函数图象上的“友好点”对数的情况为( )
A.有1对或2对 B.只有1对 C.只有2对 D.有2对或3对
9.如图,Rt△ABC中,∠ACB=90°,BC=2AC.正方形DEFG如图放置,点D,G分别在AC,BC上,E,F都在边AB上,若AB=14,则EF的长为( )
A.2 B.4 C.2 D.8
10.在Rt△ABC中,∠C=90°,CD⊥AB于点D,AB=13,CD=6,则AC+BC=( )
A.5 B.5 C.13 D.9
二、填空题
11.江边有一处高10米,背水坡角为的防洪大堤,大堤的横截面为梯形,其中,(如图).某防洪指挥部发现该大堤急需加固,经调查论证,防洪指挥部专家组制定的加固方案是沿背水坡面用土石进行加固,使上底加宽3米,加固后背水坡的坡比为.则加固后坝底增加的宽度 米.
12.已知a,b是一元二次方程x2﹣2x﹣2020=0的两个根,则a2+2b﹣3的值等于 .
13.如图,在Rt△ABC中,∠ACB=90°,点D在AB边上,将△CBD沿CD折叠,使点B恰好落在AC边上的点E处.若∠A=26°,则∠CDE= .
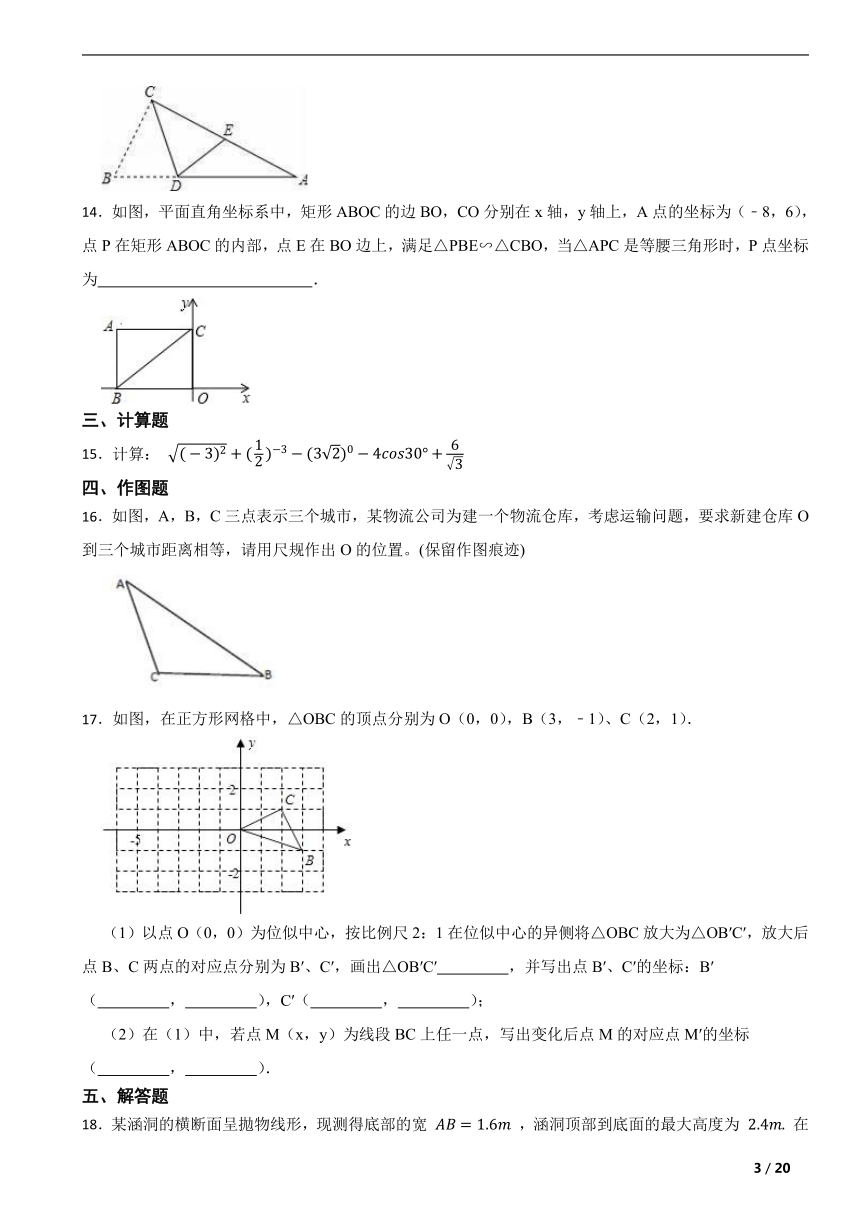
14.如图,平面直角坐标系中,矩形ABOC的边BO,CO分别在x轴,y轴上,A点的坐标为(﹣8,6),点P在矩形ABOC的内部,点E在BO边上,满足△PBE∽△CBO,当△APC是等腰三角形时,P点坐标为 .
三、计算题
15.计算:
四、作图题
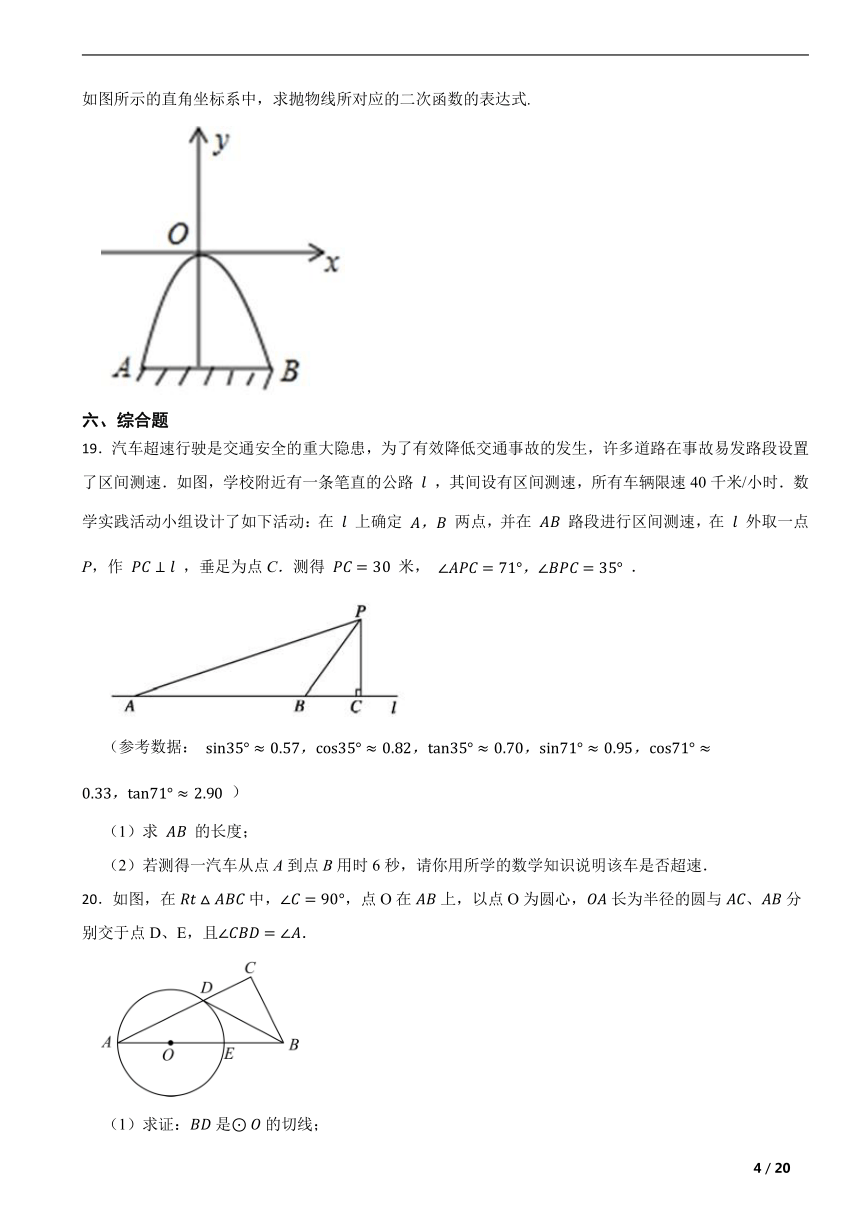
16.如图,A,B,C三点表示三个城市,某物流公司为建一个物流仓库,考虑运输问题,要求新建仓库O到三个城市距离相等,请用尺规作出O的位置。(保留作图痕迹)
17.如图,在正方形网格中,△OBC的顶点分别为O(0,0),B(3,﹣1)、C(2,1).
(1)以点O(0,0)为位似中心,按比例尺2:1在位似中心的异侧将△OBC放大为△OB′C′,放大后点B、C两点的对应点分别为B′、C′,画出△OB′C′ ,并写出点B′、C′的坐标:B′( , ),C′( , );
(2)在(1)中,若点M(x,y)为线段BC上任一点,写出变化后点M的对应点M′的坐标( , ).
五、解答题
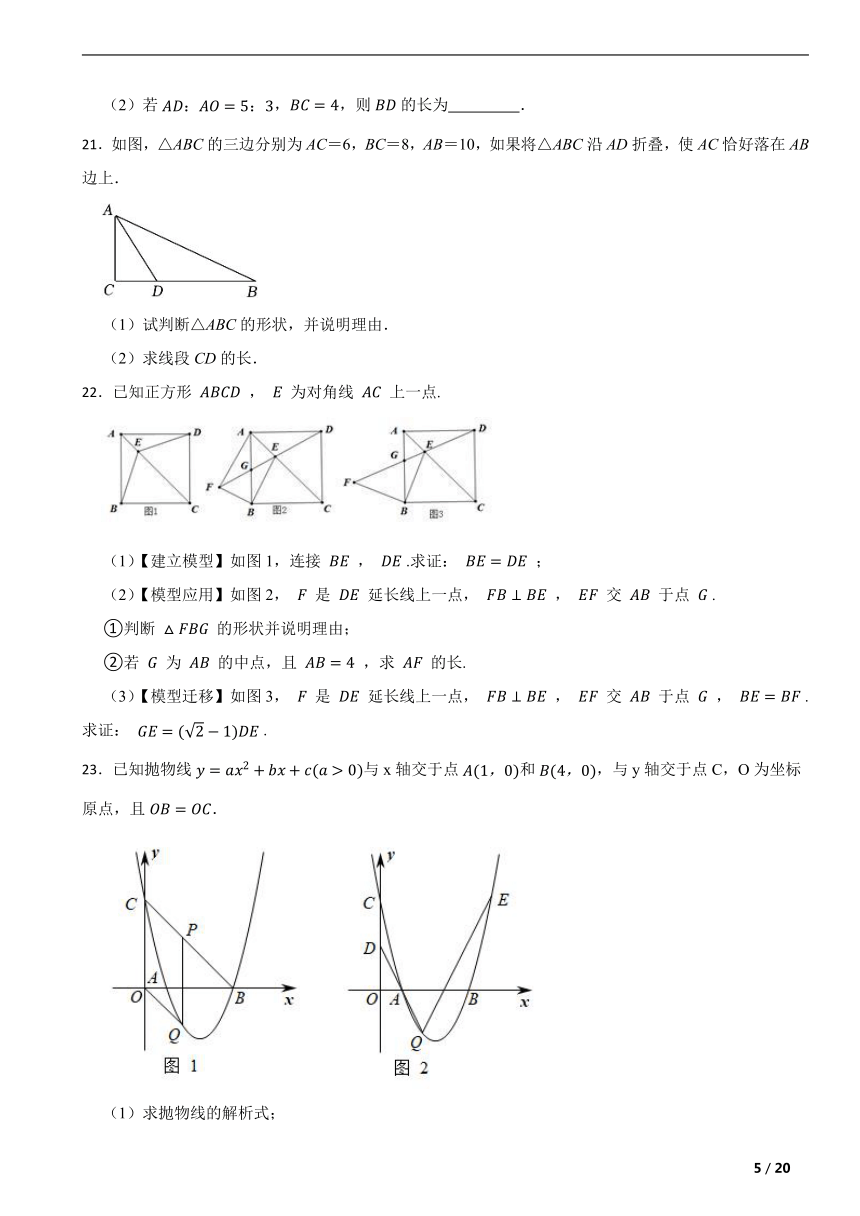
18.某涵洞的横断面呈拋物线形,现测得底部的宽 ,涵洞顶部到底面的最大高度为 在如图所示的直角坐标系中,求抛物线所对应的二次函数的表达式.
六、综合题
19.汽车超速行驶是交通安全的重大隐患,为了有效降低交通事故的发生,许多道路在事故易发路段设置了区间测速.如图,学校附近有一条笔直的公路 ,其间设有区间测速,所有车辆限速40千米/小时.数学实践活动小组设计了如下活动:在 上确定 两点,并在 路段进行区间测速,在 外取一点P,作 ,垂足为点C.测得 米, .
(参考数据: )
(1)求 的长度;
(2)若测得一汽车从点A到点B用时6秒,请你用所学的数学知识说明该车是否超速.
20.如图,在中,,点O在上,以点O为圆心,长为半径的圆与、分别交于点D、E,且.
(1)求证:是的切线;
(2)若,,则的长为 .
21.如图,△ABC的三边分别为AC=6,BC=8,AB=10,如果将△ABC沿AD折叠,使AC恰好落在AB边上.
(1)试判断△ABC的形状,并说明理由.
(2)求线段CD的长.
22.已知正方形 , 为对角线 上一点.
(1)【建立模型】如图1,连接 , .求证: ;
(2)【模型应用】如图2, 是 延长线上一点, , 交 于点 .
①判断 的形状并说明理由;
②若 为 的中点,且 ,求 的长.
(3)【模型迁移】如图3, 是 延长线上一点, , 交 于点 , .求证: .
23.已知抛物线与x轴交于点和,与y轴交于点C,O为坐标原点,且.
(1)求抛物线的解析式;
(2)如图1,点P是线段上的一个动点(不与点B、C重合),过点P作x轴的垂线交抛物线于点Q,连接.当四边形恰好是平行四边形时,求点Q的坐标;
(3)如图2,在(2)的条件下,是的中点,过点Q的直线与抛物线交于点E,且,在直线上是否存在点F,使得与相似?若存在,求点F的坐标:若不存在,请说明理由.
答案解析部分
1.【答案】B
【解析】【解答】根据轴对称的定义知:第二个与第四个时轴对称图形.
故答案为:B.
【分析】轴对称图形:一个图形沿一条直线折叠,直线两旁的部分能够完全重合的图形;据此逐一判断即可.
2.【答案】C
【解析】【解答】∵AD∥BE∥CF,∴ .
∵AB=3,BC=6,DE=2,∴ ,∴EF=4.
故答案为:C.
【分析】根据平行线分线段成比例定理,可得,代入数据计算即得.
3.【答案】A
【解析】【解答】解: ,
∵
平分 ,
.
故答案为:A.
【分析】根据∠BEF=∠BEP+∠PEF可得∠BEF的度数,由平行线的性质可得∠BEF+∠EFD=180°,求出∠EFD的度数,由角平分线的概念可得∠EFP的度数,然后结合内角和定理进行求解.
4.【答案】B
【解析】【解答】把、 两点分别代入,
得到 =,c=,
根据 可以得出b-c<0,
所以,
故答案为:B
【分析】把、 两点分别代入中,可得=,c=,由可得>,从而得解.
5.【答案】C
【解析】【解答】解:在Rt△ABC中,∠BAC=90°,sinB= ,
∵AD⊥BC,
∴sinB= ,
sinB=sin∠DAC= ,
综上,只有C不正确
故选:C.
【分析】根据锐角三角函数的定义,即可解答.
6.【答案】C
【解析】【解答】解:令即:
解得:
∴小朱本次投掷实心球的成绩为8米,
故答案为:C.
【分析】当此时x的值,即为小朱本次投掷实心球的成绩.
7.【答案】D
【解析】【解答】解:将x=0代入y=(x﹣1)2+2,得y=3,
所以抛物线与y轴的交点坐标是(0,3).
故选D.
【分析】将x=0代入y=(x﹣1)2+2,计算即可求得抛物线与y轴的交点坐标.
8.【答案】A
【解析】【解答】解:设A(a,﹣ ),
由题意知,点A关于原点的对称点B(-a, ),在直线y2=kx+1+k上,
则 =﹣ak+1+k,
整理,得:ka2﹣(k+1)a+1=0 ①,
即(a﹣1)(ka﹣1)=0,
∴a﹣1=0或ka﹣1=0,
则a=1或ka﹣1=0,
若k=0,则a=1,此时方程①只有1个实数根,即两个函数图象上的“友好点”只有1对;
若k≠0,则a= ,此时方程①有2个实数根,即两个函数图象上的“友好点”有2对,
综上,这两个函数图象上的“友好点”对数情况为1对或2对,
故选:A.
【分析】根据“友好点”的定义知,函数y1图象上点A(a,﹣ )关于原点的对称点B(-a, )一定位于直线y2上,即方程ka2﹣(k+1)a+1=0 有解,整理方程得(a﹣1)(ka﹣1)=0,据此可得答案.
9.【答案】B
【解析】【解答】解:作CH⊥AB于H,交DG于K.设EF=x,则DG=DE=FG=x.
在Rt△ACB中,∵∠ACB=90°,BC=2AC,AB=14,
∴AC= ,
∴ ,
∵DG∥AB,
∴△CDG∽△CAB,
∴ ,
∴ ,
解得x=4,
∴EF=4。
故答案为:B。
【分析】作CH⊥AB于H,交DG于K.设EF=x,则DG=DE=FG=x,在Rt△ACB中,利用勾股定理算出AC,BC的长,根据三角形的面积法由AC·BC=AB·CH算出CH的长,根据正方形的性质得出DG∥AB,根据平行于三角形一边的直线截其它两边,所截的三角形与原三角形相似得出△CDG∽△CAB,根据相似三角形对应边成比例得出,根据比例式建立方程,求解算出EF的长。
10.【答案】B
【解析】【解答】解:∵S△ABC= AB CD= AC BC,AB=13,CD=6,
∴AC BC=13×6=78,
∵△ABC为直角三角形,
∴根据勾股定理得:AB =AC +BC =169,
∴(AC+BC) =AC +2AC BC+BC =169+156=325,
则AC+BC= =5 .
故选:B.
11.【答案】
【解析】【解答】解:∵四边形ABCD为梯形,
∴DC∥AB,
∴DG=EH且DG∥EH,
∴四边形EDGH为矩形,
∴ED=GH.
∵∠DAB=45°,
∴DG=AG=10米.
∵i=,
∴FH=10÷=米,
∴AF=FH+HG-AG=+3-10=-7.
故答案为:-7.
【分析】易得四边形EDGH为矩形,则ED=GH=3,由三角函数的概念可得DG=AG=10米,根据背水坡EF的坡比可求出FH的值,然后根据AF=FH+HG-AG进行计算.
12.【答案】2021
【解析】【解答】解:∵a是一元二次方程的一个根,
∴ ,
再由根与系数的关系可知: ,
∴a2+2b 3
=a2 2a+2a+2b 3,
=2020+2(a+b) 3
=2020+2×2 3
=2021,
故答案为:2021.
【分析】根据一元二次方程的根与系数的关系得出 ,根据方程根的定义可知 ,从而将代数式变形后整体代入即可算出答案.
13.【答案】71°
【解析】【解答】解:∵∠A=26°,∴∠B=90°-26°=64°,
∴∠CED=∠B=64°,
∵∠CED=∠EDC+∠A,∴∠EDC=∠CED-∠A=64°-26°=38°,
∴∠CDE=∠CDB=(180°-38°)÷2=71°.
故答案为:71°.
【分析】由余角的性质求出∠B的度数,则由折叠的性质得出∠CED的度数,然后很据三角形外角的性质求出∠EDC,最后根据折叠的性质,结合平角的定义列式即可求出∠CDE的度数.
14.【答案】 或(-4,3)
【解析】【解答】解:∵点P在矩形ABOC的内部,且△APC是等腰三角形,
∴P点在AC的垂直平分线上或在以点C为圆心AC为半径的圆弧上;
①当P点在AC的垂直平分线上时,点P同时在BC上,AC的垂直平分线与BO的交点即是E,如图1所示:
∵PE⊥BO,CO⊥BO,
∴PE∥CO,
∴△PBE∽△CBO,
∵四边形ABOC是矩形,A点的坐标为(﹣8,6),
∴点P横坐标为﹣4,OC=6,BO=8,BE=4,
∵△PBE∽△CBO,
∴ = ,即 = ,
解得:PE=3,
∴点P(﹣4,3);
②P点在以点C为圆心AC为半径的圆弧上,圆弧与BC的交点为P,
过点P作PE⊥BO于E,如图2所示:
∵CO⊥BO,
∴PE∥CO,
∴△PBE∽△CBO,
∵四边形ABOC是矩形,A点的坐标为(﹣8,6),
∴AC=BO=8,CP=8,AB=OC=6,
∴BC= = =10,
∴BP=2,
∵△PBE∽△CBO,
∴ = = ,即: = = ,
解得:PE= ,BE= ,
∴OE=8﹣ = ,
∴点P(﹣ , );
综上所述:点P的坐标为:(﹣ , )或(﹣4,3);
故答案为(﹣ , )或(﹣4,3).
【分析】由题意得出P点在AC的垂直平分线上或在以点C为圆心AC为半径的圆弧上;
①当P点在AC的垂直平分线上时,点P同时在BC上,AC的垂直平分线与BO的交点即是E,证出PE∥CO,则△PBE∽△CBO,由已知得出点P横坐标为﹣4,OC=6,BO=8,BE=4,由相似对应边成比例得出PE=3即可得出结果;
②P点在以点C为圆心AC为半径的圆弧上,圆弧与BC的交点为P,过点P作PE⊥BO于E,证出PE∥CO,则△PBE∽△CBO,由已知得出AC=BO=8,CP=8,AB=OC=6,由勾股定理得出BC= =10,则BP=2,由相似对应边成比例得出PE= ,BE= ,则OE= 即可得出结果.
15.【答案】解:原式=3+8 1 4× +2 =10 2 +2 =10
【解析】【分析】根据二次根式的性质,负指数的意义,0指数的意义,特殊锐角三角函数值,分别化简,再根据实数的运算法则算出结果。
16.【答案】如图所示,分别作AB、BC的垂直平分线,交点O即为仓库的位置.
【解析】【分析】根据线段垂直平分线的性质可知作△ABC任意两边的中垂线,交点O即为仓库的位置.
17.【答案】(1);﹣6;2;﹣4;﹣2
(2)﹣2x;﹣2y
【解析】【解答】解:(1)如图
B′(﹣6,2),C′(﹣4,﹣2)
2)M′(﹣2x,﹣2y).
【分析】(1)延长BO,CO,根据相似比,在延长线上分别截取AO,BO,CO的2倍,确定所作的位似图形的关键点A',B',C'再顺次连接所作各点,即可得到放大2倍的位似图形△OB'C';再根据点的位置写出点的坐标即可;(2)M′的坐标的横坐标、纵坐标分别是M的坐标的2倍的相反数.
18.【答案】解:设此抛物线所对应的函数表达式为: ,
,涵洞顶点O到水面的距离为 ,
点坐标应该是 ,
把A点代入得: ,
解得: ,
故涵洞所在抛物线的函数表达式 .
【解析】【分析】由题意可设抛物线的解析式为:y=ax2,结合已知易得点A的坐标为(-0.8,-2.4),把点A的坐标代入抛物线的解析式计算即可求解.
19.【答案】(1)解:在 中,
在 中
;
(2)解: 该汽车的实际速度
又
该车没有超速.
【解析】【分析】先求出,,据此得出,从而求出该车通过AB段的车速,比较大小即可。
20.【答案】(1)证明:连接,
∵,
∴,
∵,
∴,
∵,
∴,
∴,
为半径
∴与相切;
(2)
【解析】【解答】(2)解:连接,
∴,
∵,,
∴,
∴,
∵,
∴设,则,,
∵,
∴,
∴.
【分析】(1)连接OD,先求出,再结合OD为半径,可证出与相切;
(2)连接DE,先证出,可得,再设,则,,将数据代入可得,再求出即可。
21.【答案】(1)解:△ABC是直角三角形;
理由:∵AC2+BC2=62+82=100=AB2,
∴∠C=90°;
∴△ABC是直角三角形.
(2)解:设折叠后点C与AB上的点E重合.
设CD=x,则DE=x,AE=6,BE=4,BD=8﹣x;
∵∠AED=∠C=90°,
在Rt△EBD中,x2+42=(8﹣x)2,
解得:x=3.
即线段CD的长为3.
【解析】【分析】(1)根据勾股定理的逆定理即可求出答案;
(2)设折叠后点C与AB上的点E重合,CD=x,则DE=x,AE=6,BE=4,BD=8﹣x,在Rt△EBD中,根据勾股定理列出方程,解方程即可求出答案.
22.【答案】(1)证明:∵四边形 为正方形, 为对角线,
∴ , .
∵ ,
∴ ,
∴
(2)解:① 为等腰三角形.理由如下:
∵四边形 为正方形,
∴ ,
∴ .
∵ ,
∴ ,
由(1)得 ,
∴ ,
又∵ ,
∴ ,
∴ 为等腰三角形.
②如图1,过点 作 ,垂足为 .
∵四边形 为正方形,点 为 的中点, ,
∴ , .
由①知 ,
∴ ,
∴ .
在 与 中,
∵ ,
∴ ,
∴ ,
∴ .
在 中, .
(3)证明:如图2,
∵ ,
∴ .
在 中, ,
∴ .
由(1)得 ,
由(2)得 ,
∴ .
【解析】【分析】(1)根据正方形的性质可得AB=AD,∠BAE=∠DAE=45°,证明△ABE≌△ADE,据此可得结论;
(2)①根据正方形的性质可得∠GAD=90°,根据垂直的概念可得∠EBF=90°,由(1)得∠ADG=∠EBG,根据等角的余角相等可得∠AGD=∠FBG,根据对顶角的性质可得∠AGD=∠FGB,推出∠FBG=∠FGB,据此判断;
②过点F作FH⊥AB,垂足为H,根据正方形的性质以及中点的概念可得AG=BG=2,AD=4,由①知FG=FB,则GH=BH=1,AH=AG+GH=3,根据对顶角的性质可得∠FGH=∠DGA,结合三角函数的概念可得FH,然后利用勾股定理计算即可;
(3)根据垂直的概念可得∠FBE=90°,则EF=BE,由(1)得BE=DE,由(2)得FG=BF,然后根据GE=EF-FG进行解答.
23.【答案】(1)解:设抛物线的解析式为,
∵,,
∴
代入,得,
解得,
∴抛物线的解析式为;
(2)解:设直线的解析式为,
代入得,
∴,
∴直线的解析式为,
设,,则,
则,
∵是平行四边形,
∴,即,
∴,
∴;
(3)解:由题意得,,,
∴点D、A、Q在同直线上,
设,,
∴,,
作轴,故轴,则,
∴,
∵,
∴,
可知,
∴,
同理可得直线的解析式为,
解方程,得或,
∴,
连接,作轴,
可知:,
∴,
∵,
∴,
即,故F在E的左侧,
此时:,
设,
∵,,,,
I.当时,
,
∴,,
∴,
II.当时,
,
∴,,
∴.
【解析】【分析】(1)利用待定系数法求出抛物线的解析式即可;
(2)先求出直线的解析式为,设,则,可PQ =-p2+4p,由平行四边形的性质可得CO=PQ,据此建立方程并解之即可;
(3)先判断点D、A、Q在同直线上,设,,可得,, 作轴,故轴,则, 可推出,可知,即得
,求出直线的解析式为, 联立二次函数解析式为方程组并解之,可得E(5,4), 连接,作轴,可知,即得,再推出,故F在E的左侧, 此时,设, 分两种情况:I.当时, II.当时, 根据相似三角形见的性质分别求解即可.
1 / 1
一、选择题
1.下列图形中,轴对称图形的个数是( )
A.1个 B.2个 C.3个 D.4个
2.如图,AD∥BE∥CF,AB=3,BC=6,DE=2,则EF的值为( )
A.2 B.3 C.4 D.5
3.如图, , 与 , 分别相交于点 , , ,与 的平分线 相交于点 ,且 ,则 的度数( )
A.70° B.65° C.60° D.55°
4.若,两点均在函数的图象上,且,则与的大小关系为( )
A. B. C. D.无法判断
5.如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,则下列结论不正确的是( )
A. B. C. D.
6.如图,在九年级体育测试中,小朱掷出的实心球的飞行高度y(米)与水平距离x(米)之间的关系大致满足二次函数,则小朱本次投掷实心球的成绩为( )
A.7m B.7.5m C.8m D.8.5m
7.抛物线y=(x﹣1)2+2与y轴交点坐标为( )
A.(0,1) B.(0,2) C.(1,2) D.(0,3)
8.已知点A在函数y1=﹣ (x>0)的图象上,点B在直线y2=kx+1+k(k为常数,且k≥0)上.若A,B两点关于原点对称,则称点A,B为函数y1,y2图象上的一对“友好点”.请问这两个函数图象上的“友好点”对数的情况为( )
A.有1对或2对 B.只有1对 C.只有2对 D.有2对或3对
9.如图,Rt△ABC中,∠ACB=90°,BC=2AC.正方形DEFG如图放置,点D,G分别在AC,BC上,E,F都在边AB上,若AB=14,则EF的长为( )
A.2 B.4 C.2 D.8
10.在Rt△ABC中,∠C=90°,CD⊥AB于点D,AB=13,CD=6,则AC+BC=( )
A.5 B.5 C.13 D.9
二、填空题
11.江边有一处高10米,背水坡角为的防洪大堤,大堤的横截面为梯形,其中,(如图).某防洪指挥部发现该大堤急需加固,经调查论证,防洪指挥部专家组制定的加固方案是沿背水坡面用土石进行加固,使上底加宽3米,加固后背水坡的坡比为.则加固后坝底增加的宽度 米.
12.已知a,b是一元二次方程x2﹣2x﹣2020=0的两个根,则a2+2b﹣3的值等于 .
13.如图,在Rt△ABC中,∠ACB=90°,点D在AB边上,将△CBD沿CD折叠,使点B恰好落在AC边上的点E处.若∠A=26°,则∠CDE= .
14.如图,平面直角坐标系中,矩形ABOC的边BO,CO分别在x轴,y轴上,A点的坐标为(﹣8,6),点P在矩形ABOC的内部,点E在BO边上,满足△PBE∽△CBO,当△APC是等腰三角形时,P点坐标为 .
三、计算题
15.计算:
四、作图题
16.如图,A,B,C三点表示三个城市,某物流公司为建一个物流仓库,考虑运输问题,要求新建仓库O到三个城市距离相等,请用尺规作出O的位置。(保留作图痕迹)
17.如图,在正方形网格中,△OBC的顶点分别为O(0,0),B(3,﹣1)、C(2,1).
(1)以点O(0,0)为位似中心,按比例尺2:1在位似中心的异侧将△OBC放大为△OB′C′,放大后点B、C两点的对应点分别为B′、C′,画出△OB′C′ ,并写出点B′、C′的坐标:B′( , ),C′( , );
(2)在(1)中,若点M(x,y)为线段BC上任一点,写出变化后点M的对应点M′的坐标( , ).
五、解答题
18.某涵洞的横断面呈拋物线形,现测得底部的宽 ,涵洞顶部到底面的最大高度为 在如图所示的直角坐标系中,求抛物线所对应的二次函数的表达式.
六、综合题
19.汽车超速行驶是交通安全的重大隐患,为了有效降低交通事故的发生,许多道路在事故易发路段设置了区间测速.如图,学校附近有一条笔直的公路 ,其间设有区间测速,所有车辆限速40千米/小时.数学实践活动小组设计了如下活动:在 上确定 两点,并在 路段进行区间测速,在 外取一点P,作 ,垂足为点C.测得 米, .
(参考数据: )
(1)求 的长度;
(2)若测得一汽车从点A到点B用时6秒,请你用所学的数学知识说明该车是否超速.
20.如图,在中,,点O在上,以点O为圆心,长为半径的圆与、分别交于点D、E,且.
(1)求证:是的切线;
(2)若,,则的长为 .
21.如图,△ABC的三边分别为AC=6,BC=8,AB=10,如果将△ABC沿AD折叠,使AC恰好落在AB边上.
(1)试判断△ABC的形状,并说明理由.
(2)求线段CD的长.
22.已知正方形 , 为对角线 上一点.
(1)【建立模型】如图1,连接 , .求证: ;
(2)【模型应用】如图2, 是 延长线上一点, , 交 于点 .
①判断 的形状并说明理由;
②若 为 的中点,且 ,求 的长.
(3)【模型迁移】如图3, 是 延长线上一点, , 交 于点 , .求证: .
23.已知抛物线与x轴交于点和,与y轴交于点C,O为坐标原点,且.
(1)求抛物线的解析式;
(2)如图1,点P是线段上的一个动点(不与点B、C重合),过点P作x轴的垂线交抛物线于点Q,连接.当四边形恰好是平行四边形时,求点Q的坐标;
(3)如图2,在(2)的条件下,是的中点,过点Q的直线与抛物线交于点E,且,在直线上是否存在点F,使得与相似?若存在,求点F的坐标:若不存在,请说明理由.
答案解析部分
1.【答案】B
【解析】【解答】根据轴对称的定义知:第二个与第四个时轴对称图形.
故答案为:B.
【分析】轴对称图形:一个图形沿一条直线折叠,直线两旁的部分能够完全重合的图形;据此逐一判断即可.
2.【答案】C
【解析】【解答】∵AD∥BE∥CF,∴ .
∵AB=3,BC=6,DE=2,∴ ,∴EF=4.
故答案为:C.
【分析】根据平行线分线段成比例定理,可得,代入数据计算即得.
3.【答案】A
【解析】【解答】解: ,
∵
平分 ,
.
故答案为:A.
【分析】根据∠BEF=∠BEP+∠PEF可得∠BEF的度数,由平行线的性质可得∠BEF+∠EFD=180°,求出∠EFD的度数,由角平分线的概念可得∠EFP的度数,然后结合内角和定理进行求解.
4.【答案】B
【解析】【解答】把、 两点分别代入,
得到 =,c=,
根据 可以得出b-c<0,
所以,
故答案为:B
【分析】把、 两点分别代入中,可得=,c=,由可得>,从而得解.
5.【答案】C
【解析】【解答】解:在Rt△ABC中,∠BAC=90°,sinB= ,
∵AD⊥BC,
∴sinB= ,
sinB=sin∠DAC= ,
综上,只有C不正确
故选:C.
【分析】根据锐角三角函数的定义,即可解答.
6.【答案】C
【解析】【解答】解:令即:
解得:
∴小朱本次投掷实心球的成绩为8米,
故答案为:C.
【分析】当此时x的值,即为小朱本次投掷实心球的成绩.
7.【答案】D
【解析】【解答】解:将x=0代入y=(x﹣1)2+2,得y=3,
所以抛物线与y轴的交点坐标是(0,3).
故选D.
【分析】将x=0代入y=(x﹣1)2+2,计算即可求得抛物线与y轴的交点坐标.
8.【答案】A
【解析】【解答】解:设A(a,﹣ ),
由题意知,点A关于原点的对称点B(-a, ),在直线y2=kx+1+k上,
则 =﹣ak+1+k,
整理,得:ka2﹣(k+1)a+1=0 ①,
即(a﹣1)(ka﹣1)=0,
∴a﹣1=0或ka﹣1=0,
则a=1或ka﹣1=0,
若k=0,则a=1,此时方程①只有1个实数根,即两个函数图象上的“友好点”只有1对;
若k≠0,则a= ,此时方程①有2个实数根,即两个函数图象上的“友好点”有2对,
综上,这两个函数图象上的“友好点”对数情况为1对或2对,
故选:A.
【分析】根据“友好点”的定义知,函数y1图象上点A(a,﹣ )关于原点的对称点B(-a, )一定位于直线y2上,即方程ka2﹣(k+1)a+1=0 有解,整理方程得(a﹣1)(ka﹣1)=0,据此可得答案.
9.【答案】B
【解析】【解答】解:作CH⊥AB于H,交DG于K.设EF=x,则DG=DE=FG=x.
在Rt△ACB中,∵∠ACB=90°,BC=2AC,AB=14,
∴AC= ,
∴ ,
∵DG∥AB,
∴△CDG∽△CAB,
∴ ,
∴ ,
解得x=4,
∴EF=4。
故答案为:B。
【分析】作CH⊥AB于H,交DG于K.设EF=x,则DG=DE=FG=x,在Rt△ACB中,利用勾股定理算出AC,BC的长,根据三角形的面积法由AC·BC=AB·CH算出CH的长,根据正方形的性质得出DG∥AB,根据平行于三角形一边的直线截其它两边,所截的三角形与原三角形相似得出△CDG∽△CAB,根据相似三角形对应边成比例得出,根据比例式建立方程,求解算出EF的长。
10.【答案】B
【解析】【解答】解:∵S△ABC= AB CD= AC BC,AB=13,CD=6,
∴AC BC=13×6=78,
∵△ABC为直角三角形,
∴根据勾股定理得:AB =AC +BC =169,
∴(AC+BC) =AC +2AC BC+BC =169+156=325,
则AC+BC= =5 .
故选:B.
11.【答案】
【解析】【解答】解:∵四边形ABCD为梯形,
∴DC∥AB,
∴DG=EH且DG∥EH,
∴四边形EDGH为矩形,
∴ED=GH.
∵∠DAB=45°,
∴DG=AG=10米.
∵i=,
∴FH=10÷=米,
∴AF=FH+HG-AG=+3-10=-7.
故答案为:-7.
【分析】易得四边形EDGH为矩形,则ED=GH=3,由三角函数的概念可得DG=AG=10米,根据背水坡EF的坡比可求出FH的值,然后根据AF=FH+HG-AG进行计算.
12.【答案】2021
【解析】【解答】解:∵a是一元二次方程的一个根,
∴ ,
再由根与系数的关系可知: ,
∴a2+2b 3
=a2 2a+2a+2b 3,
=2020+2(a+b) 3
=2020+2×2 3
=2021,
故答案为:2021.
【分析】根据一元二次方程的根与系数的关系得出 ,根据方程根的定义可知 ,从而将代数式变形后整体代入即可算出答案.
13.【答案】71°
【解析】【解答】解:∵∠A=26°,∴∠B=90°-26°=64°,
∴∠CED=∠B=64°,
∵∠CED=∠EDC+∠A,∴∠EDC=∠CED-∠A=64°-26°=38°,
∴∠CDE=∠CDB=(180°-38°)÷2=71°.
故答案为:71°.
【分析】由余角的性质求出∠B的度数,则由折叠的性质得出∠CED的度数,然后很据三角形外角的性质求出∠EDC,最后根据折叠的性质,结合平角的定义列式即可求出∠CDE的度数.
14.【答案】 或(-4,3)
【解析】【解答】解:∵点P在矩形ABOC的内部,且△APC是等腰三角形,
∴P点在AC的垂直平分线上或在以点C为圆心AC为半径的圆弧上;
①当P点在AC的垂直平分线上时,点P同时在BC上,AC的垂直平分线与BO的交点即是E,如图1所示:
∵PE⊥BO,CO⊥BO,
∴PE∥CO,
∴△PBE∽△CBO,
∵四边形ABOC是矩形,A点的坐标为(﹣8,6),
∴点P横坐标为﹣4,OC=6,BO=8,BE=4,
∵△PBE∽△CBO,
∴ = ,即 = ,
解得:PE=3,
∴点P(﹣4,3);
②P点在以点C为圆心AC为半径的圆弧上,圆弧与BC的交点为P,
过点P作PE⊥BO于E,如图2所示:
∵CO⊥BO,
∴PE∥CO,
∴△PBE∽△CBO,
∵四边形ABOC是矩形,A点的坐标为(﹣8,6),
∴AC=BO=8,CP=8,AB=OC=6,
∴BC= = =10,
∴BP=2,
∵△PBE∽△CBO,
∴ = = ,即: = = ,
解得:PE= ,BE= ,
∴OE=8﹣ = ,
∴点P(﹣ , );
综上所述:点P的坐标为:(﹣ , )或(﹣4,3);
故答案为(﹣ , )或(﹣4,3).
【分析】由题意得出P点在AC的垂直平分线上或在以点C为圆心AC为半径的圆弧上;
①当P点在AC的垂直平分线上时,点P同时在BC上,AC的垂直平分线与BO的交点即是E,证出PE∥CO,则△PBE∽△CBO,由已知得出点P横坐标为﹣4,OC=6,BO=8,BE=4,由相似对应边成比例得出PE=3即可得出结果;
②P点在以点C为圆心AC为半径的圆弧上,圆弧与BC的交点为P,过点P作PE⊥BO于E,证出PE∥CO,则△PBE∽△CBO,由已知得出AC=BO=8,CP=8,AB=OC=6,由勾股定理得出BC= =10,则BP=2,由相似对应边成比例得出PE= ,BE= ,则OE= 即可得出结果.
15.【答案】解:原式=3+8 1 4× +2 =10 2 +2 =10
【解析】【分析】根据二次根式的性质,负指数的意义,0指数的意义,特殊锐角三角函数值,分别化简,再根据实数的运算法则算出结果。
16.【答案】如图所示,分别作AB、BC的垂直平分线,交点O即为仓库的位置.
【解析】【分析】根据线段垂直平分线的性质可知作△ABC任意两边的中垂线,交点O即为仓库的位置.
17.【答案】(1);﹣6;2;﹣4;﹣2
(2)﹣2x;﹣2y
【解析】【解答】解:(1)如图
B′(﹣6,2),C′(﹣4,﹣2)
2)M′(﹣2x,﹣2y).
【分析】(1)延长BO,CO,根据相似比,在延长线上分别截取AO,BO,CO的2倍,确定所作的位似图形的关键点A',B',C'再顺次连接所作各点,即可得到放大2倍的位似图形△OB'C';再根据点的位置写出点的坐标即可;(2)M′的坐标的横坐标、纵坐标分别是M的坐标的2倍的相反数.
18.【答案】解:设此抛物线所对应的函数表达式为: ,
,涵洞顶点O到水面的距离为 ,
点坐标应该是 ,
把A点代入得: ,
解得: ,
故涵洞所在抛物线的函数表达式 .
【解析】【分析】由题意可设抛物线的解析式为:y=ax2,结合已知易得点A的坐标为(-0.8,-2.4),把点A的坐标代入抛物线的解析式计算即可求解.
19.【答案】(1)解:在 中,
在 中
;
(2)解: 该汽车的实际速度
又
该车没有超速.
【解析】【分析】先求出,,据此得出,从而求出该车通过AB段的车速,比较大小即可。
20.【答案】(1)证明:连接,
∵,
∴,
∵,
∴,
∵,
∴,
∴,
为半径
∴与相切;
(2)
【解析】【解答】(2)解:连接,
∴,
∵,,
∴,
∴,
∵,
∴设,则,,
∵,
∴,
∴.
【分析】(1)连接OD,先求出,再结合OD为半径,可证出与相切;
(2)连接DE,先证出,可得,再设,则,,将数据代入可得,再求出即可。
21.【答案】(1)解:△ABC是直角三角形;
理由:∵AC2+BC2=62+82=100=AB2,
∴∠C=90°;
∴△ABC是直角三角形.
(2)解:设折叠后点C与AB上的点E重合.
设CD=x,则DE=x,AE=6,BE=4,BD=8﹣x;
∵∠AED=∠C=90°,
在Rt△EBD中,x2+42=(8﹣x)2,
解得:x=3.
即线段CD的长为3.
【解析】【分析】(1)根据勾股定理的逆定理即可求出答案;
(2)设折叠后点C与AB上的点E重合,CD=x,则DE=x,AE=6,BE=4,BD=8﹣x,在Rt△EBD中,根据勾股定理列出方程,解方程即可求出答案.
22.【答案】(1)证明:∵四边形 为正方形, 为对角线,
∴ , .
∵ ,
∴ ,
∴
(2)解:① 为等腰三角形.理由如下:
∵四边形 为正方形,
∴ ,
∴ .
∵ ,
∴ ,
由(1)得 ,
∴ ,
又∵ ,
∴ ,
∴ 为等腰三角形.
②如图1,过点 作 ,垂足为 .
∵四边形 为正方形,点 为 的中点, ,
∴ , .
由①知 ,
∴ ,
∴ .
在 与 中,
∵ ,
∴ ,
∴ ,
∴ .
在 中, .
(3)证明:如图2,
∵ ,
∴ .
在 中, ,
∴ .
由(1)得 ,
由(2)得 ,
∴ .
【解析】【分析】(1)根据正方形的性质可得AB=AD,∠BAE=∠DAE=45°,证明△ABE≌△ADE,据此可得结论;
(2)①根据正方形的性质可得∠GAD=90°,根据垂直的概念可得∠EBF=90°,由(1)得∠ADG=∠EBG,根据等角的余角相等可得∠AGD=∠FBG,根据对顶角的性质可得∠AGD=∠FGB,推出∠FBG=∠FGB,据此判断;
②过点F作FH⊥AB,垂足为H,根据正方形的性质以及中点的概念可得AG=BG=2,AD=4,由①知FG=FB,则GH=BH=1,AH=AG+GH=3,根据对顶角的性质可得∠FGH=∠DGA,结合三角函数的概念可得FH,然后利用勾股定理计算即可;
(3)根据垂直的概念可得∠FBE=90°,则EF=BE,由(1)得BE=DE,由(2)得FG=BF,然后根据GE=EF-FG进行解答.
23.【答案】(1)解:设抛物线的解析式为,
∵,,
∴
代入,得,
解得,
∴抛物线的解析式为;
(2)解:设直线的解析式为,
代入得,
∴,
∴直线的解析式为,
设,,则,
则,
∵是平行四边形,
∴,即,
∴,
∴;
(3)解:由题意得,,,
∴点D、A、Q在同直线上,
设,,
∴,,
作轴,故轴,则,
∴,
∵,
∴,
可知,
∴,
同理可得直线的解析式为,
解方程,得或,
∴,
连接,作轴,
可知:,
∴,
∵,
∴,
即,故F在E的左侧,
此时:,
设,
∵,,,,
I.当时,
,
∴,,
∴,
II.当时,
,
∴,,
∴.
【解析】【分析】(1)利用待定系数法求出抛物线的解析式即可;
(2)先求出直线的解析式为,设,则,可PQ =-p2+4p,由平行四边形的性质可得CO=PQ,据此建立方程并解之即可;
(3)先判断点D、A、Q在同直线上,设,,可得,, 作轴,故轴,则, 可推出,可知,即得
,求出直线的解析式为, 联立二次函数解析式为方程组并解之,可得E(5,4), 连接,作轴,可知,即得,再推出,故F在E的左侧, 此时,设, 分两种情况:I.当时, II.当时, 根据相似三角形见的性质分别求解即可.
1 / 1
