数学人教A版(2019)选择性必修第二册4.4数学归纳法 课件(共29张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第二册4.4数学归纳法 课件(共29张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 7.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-17 11:10:45 | ||
图片预览







文档简介
(共29张PPT)
人教A版高中数学(2019)选择性必修第二册第四章第四节
《 4.4 数学归纳法 》
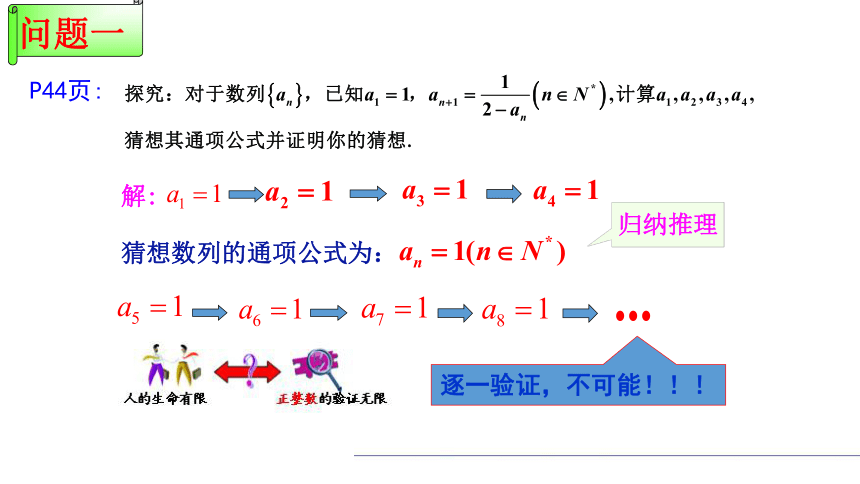
P44页:
猜想数列的通项公式为:
解:
归纳推理
逐一验证,不可能!!!
问题一
直线和平面垂直的定义:
如果直线l与平面α内的任意一条直线都垂直,我们就说直线l与平面α互相垂直,记作l⊥α.
l
平面α的垂线
平面α内任意一条直线
一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直.
m
n
P
符号表示:
文字语言:
直线和平面垂直的判定定理:
P44页:
猜想数列的通项公式为:
解:
归纳推理
逐一验证,不可能!!!
问题一
我们来欣赏一段多米诺游戏,以及感受到它给游戏者带来的意志力和创造力的培养。
多米诺骨牌(domino)是一种用木制、骨制或塑料制成的长方形骨牌。玩时将骨牌按一定间距排列成行,轻轻碰倒第一枚骨牌,其余的骨牌就会产生连锁反应,依次倒下。
多米诺是一项集动手、动脑于一体的运动。一幅图案由几百、几千甚至上万张骨牌组成。骨牌需要一张张摆下去,它不仅考验参与者的体力、耐力和意志力,而且还培养参与者的智力、想象力和创造力。
多米诺起源于中国,有着上千年的历史。
观看多米诺骨牌视屏
情境二(多米诺骨牌游戏)
通过下面实验,探索游戏原理。
?
两个条件
类比多米诺骨牌游戏,迁移证明数列猜想
⑴第1块骨牌倒下。
⑴ 当n=1时,验证猜想正确。
⑵如果第k块 倒下时,一定能导致第k+1块也倒下。
⑵如果 n=k 时猜想成立,一定能推出
根据⑴和⑵,可知不论有多少个骨牌都能全部倒下。
根据 ⑴ 和 ⑵ ,可知对所有的正整数n,猜想都成立。
当n=k+1时猜想也成立。
这样就找到有限个步骤的推理,证明n取所有正整数都成立的方法。
多米诺骨牌游戏原理
猜想数列的通项公式为:
分析:
证明:
(1)当n=1时,a1=1,显然猜想成立。
(2)假设当n=k时,猜想成立,即
ak =
那么当n=k+1时,
ak+1=
2-ak
1
=
1
1
2-
=
1
即n=k+1时,猜想成立。
根据⑴⑵可知,对n∈N*,通项恒成立.
1
类比数学问题, 激起思维浪花
完成这两个步骤后, 就可以断定命题对从n0开始的所有正整数 n都成立.
证明一个与正整数有关的命题步骤如下:
(2) 假设当n=k (k∈N*, k≥n0 ) 时命题成立,
证明当n=k+1时命题也成立.
(1) 证明当n取第一个值n = n0 时命题成立.
———这种证明方法叫做
数学归纳法
概括提炼,得出概念
例1 . 用数学归纳法证明:
分析:第一步:验证n=1时命题成立,
即证明命题
第二步:要证明命题
“假设 时成立,
那么
第三步:下结论:对任意的正整数n都成立.
两个步骤
一个结论
缺一不可
概念应用 巩固提升
).
证明: (1)当=1时, 等式左边= =1,
右边= = ,等式成立.
(2)假设当= ()时,等式成立,即=
由(1)和(2)可知,等式对任何都成立.
那么
即当= +1时,等式也成立.
目 标
).
例1 . 用数学归纳法证明:
注意点:用数学归纳法证明恒等式时,应关注以下三点:
(1)弄清n取第一个值n0时等式两端项的情况;
(2)弄清从n=k到n=k+1等式两端的变化情况,增加了哪些项,减少了哪些项;
(3)在证明n=k+1时命题成立的过程中,要设法利用假设n=k时命题成立的式子,并朝着n=k+1证明目标的表达式进行变形.
小结
对点练习1
B
对点练习2
用数学归纳法证明:
1×2+2×3+3×4+…+n(n+1) =
从n=k到n=k+1有什么变化
凑假设
凑结论
证明:
2)假设n=k时命题成立,即
1×2+2×3+3×4+…+k(k+1)=
则当n=k+1时,
+
=
=
∴ n=k+1时命题成立。 由(1)和(2)知,当 ,原命题成立。
=
1)当n=1时,左边=1×2=2,右边= =2, 命题成立.
课堂变式练习3
课堂小结
小结:通过本节课,我们学到了什么,请同学回想一下,各抒己见:
问题1. 我们为什么要学习数学归纳法?
问题2. 我们是借助什么来揭示数学归纳法原理的?
问题3. 数学归纳法的解题步骤是什么,要注意哪些事项?
问题4. 本节课用到的的数学思想与方法有哪些?
验证n = n0时命题成立.
命题对所有的正整数n ( n ≥ n0 )都成立.
归纳奠基
归纳递推
数学归纳法:
若n = k ( k ≥ n0 )时命题成立, 证明n = k+1时命题也成立.
1.两个步骤
一个结论
缺一不可
这种证明方法叫做数学归纳法.
2.利用假设
结合递推
加以证明
课堂小结
布置作业
教科书P47练习:1 、2
教科书P51复习巩固 1 、2(2)
谢谢指导
验证n = n0时命题成立.
命题对所有的正整数n ( n ≥ n0 )都成立.
归纳奠基
归纳递推
数学归纳法用框图表示:
若n = k ( k ≥ n0 ) 时命题成立, 证明n = k+1时命题也成立.
两个步骤
一个结论
缺一不可
方法归纳
求证:
证明:①当n =1时,左边=
,右边=
,等式成立.
那么,当n=k+1时,有
即n=k+1时,命题成立
根据①②可知,对n∈N*,等式成立.
②假设n =k 时,有
数学归纳法
吗?
变式练习
?
思维误区警示
求证:
证明:①当n=1时,左边=
,右边=
,等式成立.
那么,当n=k+1时,有
即n=k+1时,命题成立
根据①②可知,对n∈N*,等式成立.
②假设n =k时,有
没有用到假设
数学归纳法
吗?
变式练习
?
思维误区警示
求证:
证明:①当n=1时,左边=
,右边=
,等式成立.
那么,当n=k+1时,有
即n=k+1时,命题成立
根据①②可知,对n∈N*,等式成立.
②假设n =k时,有
数学归纳法
吗?
变式练习
?
思维误区警示
求证:
证明:①当n=1时,左边=
,右边=
,等式成立.
那么,当n=k+1时,有
即n=k+1时,命题成立
根据①②可知,对n∈N*,等式成立.
②假设n =k时,有
数学归纳法
吗?
变式练习
?
思维误区警示
求证:
证明:①当n=1时,左边=
,右边=
,等式成立.
那么,当n=k+1时,有
即n=k+1时,命题成立
根据①②可知,对n∈N*,等式成立.
②假设n =k时,有
数学归纳法
变式练习
!
吗?
当n=k+1时,此时左边比n=k时多了几项?
_______________________.
用数学归纳法证明:
1+2+3++(2n+1)=(n+1)(2n+1) (n N*)
1.当n=1时,左边= ;
1+2+3
1+2+3+4+5
3.当n=k时,左边= .
2.当n=2时,左边= .
1+2+…+(2k+1)
4.当n=k+1时, 左边=
.
1+2+…+(2k+1)+(2k+2)+(2k+3)
(2k+2),(2k+3)
当n=k+1时,右边
= .
(k+2)(2k+3)
基础练习2
人教A版高中数学(2019)选择性必修第二册第四章第四节
《 4.4 数学归纳法 》
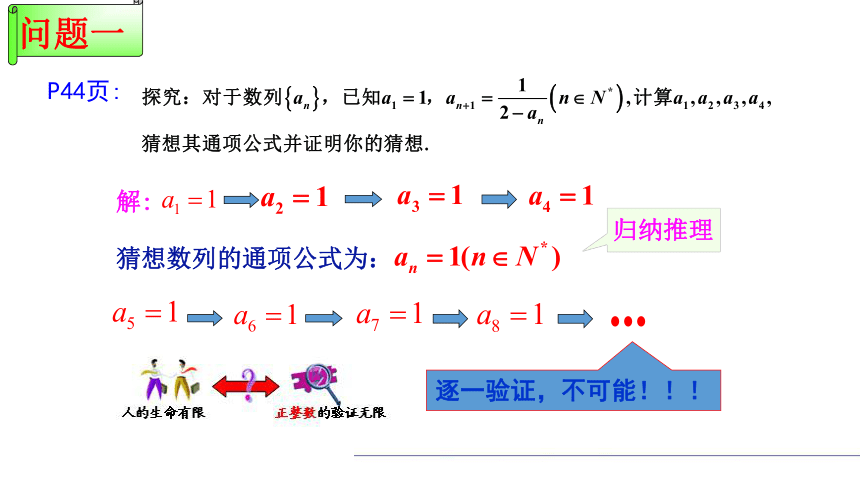
P44页:
猜想数列的通项公式为:
解:
归纳推理
逐一验证,不可能!!!
问题一
直线和平面垂直的定义:
如果直线l与平面α内的任意一条直线都垂直,我们就说直线l与平面α互相垂直,记作l⊥α.
l
平面α的垂线
平面α内任意一条直线
一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直.
m
n
P
符号表示:
文字语言:
直线和平面垂直的判定定理:
P44页:
猜想数列的通项公式为:
解:
归纳推理
逐一验证,不可能!!!
问题一
我们来欣赏一段多米诺游戏,以及感受到它给游戏者带来的意志力和创造力的培养。
多米诺骨牌(domino)是一种用木制、骨制或塑料制成的长方形骨牌。玩时将骨牌按一定间距排列成行,轻轻碰倒第一枚骨牌,其余的骨牌就会产生连锁反应,依次倒下。
多米诺是一项集动手、动脑于一体的运动。一幅图案由几百、几千甚至上万张骨牌组成。骨牌需要一张张摆下去,它不仅考验参与者的体力、耐力和意志力,而且还培养参与者的智力、想象力和创造力。
多米诺起源于中国,有着上千年的历史。
观看多米诺骨牌视屏
情境二(多米诺骨牌游戏)
通过下面实验,探索游戏原理。
?
两个条件
类比多米诺骨牌游戏,迁移证明数列猜想
⑴第1块骨牌倒下。
⑴ 当n=1时,验证猜想正确。
⑵如果第k块 倒下时,一定能导致第k+1块也倒下。
⑵如果 n=k 时猜想成立,一定能推出
根据⑴和⑵,可知不论有多少个骨牌都能全部倒下。
根据 ⑴ 和 ⑵ ,可知对所有的正整数n,猜想都成立。
当n=k+1时猜想也成立。
这样就找到有限个步骤的推理,证明n取所有正整数都成立的方法。
多米诺骨牌游戏原理
猜想数列的通项公式为:
分析:
证明:
(1)当n=1时,a1=1,显然猜想成立。
(2)假设当n=k时,猜想成立,即
ak =
那么当n=k+1时,
ak+1=
2-ak
1
=
1
1
2-
=
1
即n=k+1时,猜想成立。
根据⑴⑵可知,对n∈N*,通项恒成立.
1
类比数学问题, 激起思维浪花
完成这两个步骤后, 就可以断定命题对从n0开始的所有正整数 n都成立.
证明一个与正整数有关的命题步骤如下:
(2) 假设当n=k (k∈N*, k≥n0 ) 时命题成立,
证明当n=k+1时命题也成立.
(1) 证明当n取第一个值n = n0 时命题成立.
———这种证明方法叫做
数学归纳法
概括提炼,得出概念
例1 . 用数学归纳法证明:
分析:第一步:验证n=1时命题成立,
即证明命题
第二步:要证明命题
“假设 时成立,
那么
第三步:下结论:对任意的正整数n都成立.
两个步骤
一个结论
缺一不可
概念应用 巩固提升
).
证明: (1)当=1时, 等式左边= =1,
右边= = ,等式成立.
(2)假设当= ()时,等式成立,即=
由(1)和(2)可知,等式对任何都成立.
那么
即当= +1时,等式也成立.
目 标
).
例1 . 用数学归纳法证明:
注意点:用数学归纳法证明恒等式时,应关注以下三点:
(1)弄清n取第一个值n0时等式两端项的情况;
(2)弄清从n=k到n=k+1等式两端的变化情况,增加了哪些项,减少了哪些项;
(3)在证明n=k+1时命题成立的过程中,要设法利用假设n=k时命题成立的式子,并朝着n=k+1证明目标的表达式进行变形.
小结
对点练习1
B
对点练习2
用数学归纳法证明:
1×2+2×3+3×4+…+n(n+1) =
从n=k到n=k+1有什么变化
凑假设
凑结论
证明:
2)假设n=k时命题成立,即
1×2+2×3+3×4+…+k(k+1)=
则当n=k+1时,
+
=
=
∴ n=k+1时命题成立。 由(1)和(2)知,当 ,原命题成立。
=
1)当n=1时,左边=1×2=2,右边= =2, 命题成立.
课堂变式练习3
课堂小结
小结:通过本节课,我们学到了什么,请同学回想一下,各抒己见:
问题1. 我们为什么要学习数学归纳法?
问题2. 我们是借助什么来揭示数学归纳法原理的?
问题3. 数学归纳法的解题步骤是什么,要注意哪些事项?
问题4. 本节课用到的的数学思想与方法有哪些?
验证n = n0时命题成立.
命题对所有的正整数n ( n ≥ n0 )都成立.
归纳奠基
归纳递推
数学归纳法:
若n = k ( k ≥ n0 )时命题成立, 证明n = k+1时命题也成立.
1.两个步骤
一个结论
缺一不可
这种证明方法叫做数学归纳法.
2.利用假设
结合递推
加以证明
课堂小结
布置作业
教科书P47练习:1 、2
教科书P51复习巩固 1 、2(2)
谢谢指导
验证n = n0时命题成立.
命题对所有的正整数n ( n ≥ n0 )都成立.
归纳奠基
归纳递推
数学归纳法用框图表示:
若n = k ( k ≥ n0 ) 时命题成立, 证明n = k+1时命题也成立.
两个步骤
一个结论
缺一不可
方法归纳
求证:
证明:①当n =1时,左边=
,右边=
,等式成立.
那么,当n=k+1时,有
即n=k+1时,命题成立
根据①②可知,对n∈N*,等式成立.
②假设n =k 时,有
数学归纳法
吗?
变式练习
?
思维误区警示
求证:
证明:①当n=1时,左边=
,右边=
,等式成立.
那么,当n=k+1时,有
即n=k+1时,命题成立
根据①②可知,对n∈N*,等式成立.
②假设n =k时,有
没有用到假设
数学归纳法
吗?
变式练习
?
思维误区警示
求证:
证明:①当n=1时,左边=
,右边=
,等式成立.
那么,当n=k+1时,有
即n=k+1时,命题成立
根据①②可知,对n∈N*,等式成立.
②假设n =k时,有
数学归纳法
吗?
变式练习
?
思维误区警示
求证:
证明:①当n=1时,左边=
,右边=
,等式成立.
那么,当n=k+1时,有
即n=k+1时,命题成立
根据①②可知,对n∈N*,等式成立.
②假设n =k时,有
数学归纳法
吗?
变式练习
?
思维误区警示
求证:
证明:①当n=1时,左边=
,右边=
,等式成立.
那么,当n=k+1时,有
即n=k+1时,命题成立
根据①②可知,对n∈N*,等式成立.
②假设n =k时,有
数学归纳法
变式练习
!
吗?
当n=k+1时,此时左边比n=k时多了几项?
_______________________.
用数学归纳法证明:
1+2+3++(2n+1)=(n+1)(2n+1) (n N*)
1.当n=1时,左边= ;
1+2+3
1+2+3+4+5
3.当n=k时,左边= .
2.当n=2时,左边= .
1+2+…+(2k+1)
4.当n=k+1时, 左边=
.
1+2+…+(2k+1)+(2k+2)+(2k+3)
(2k+2),(2k+3)
当n=k+1时,右边
= .
(k+2)(2k+3)
基础练习2
