人教版八年级数学上册第十四章整式的乘法与因式分解单元复习题(含答案)
文档属性
| 名称 | 人教版八年级数学上册第十四章整式的乘法与因式分解单元复习题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 122.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-18 00:00:00 | ||
图片预览


文档简介
人教版八年级数学上册第十四章整式的乘法与因式分解单元复习题
一、单选题
1.计算 结果正确的是( )
A. B. C. D.
2.多项式分解因式时,应提取的公因式是( )
A. B. C. D.
3.下列等式从左到右的变形中,属于因式分解的是( )
A.ab+ac+d=a(b+c)+d B.(x+1)(x+3)=x2+4x+3
C.6ab=2a·3b D.x(x-y)+y(y-x)=(x-y)2
4.下列各式能用平方差公式进行分解因式的是( )
A.x2+1 B.﹣1+x2 C.﹣x2﹣y2 D.x2+4x+4
5.把多项式a3+2a2b+ab2﹣a分解因式正确的是( )
A.(a2+ab+a)(a+b+1) B.a(a+b+1)(a+b﹣1)
C.a(a2+2ab+b2﹣1) D.(a2+ab+a)(a2+ab﹣a)
6.若 , ,则M与N的大小关系是( )
A.M>N B.M7.下列各式计算正确的是( )
A.a2+2a3=3a5 B.a a2=a3
C.a6÷a2=a3 D.(a2)3=a5
8.下列运算正确的是( )
A.a2 a3=a6 B.a3÷a﹣3=1
C.(a﹣b)2=a2﹣ab+b2 D.(﹣a2)3=﹣a6
二、填空题
9.若am=9,an=3,则am-n= .
10.计算: .
11.若m-n=2,则(2m2n-2mn2)÷(mn)的值为 .
12.已知(2x-21)(3x-7)-(3x-7)(x-13)可分解因式为(3x+a)(x+b),其中a,b均为整数,则a+3b= 。
三、解答题
13.计算题:
(1)(a2)3 (a2)4÷(a2)5
(2)(x﹣y+9)(x+y﹣9)
14.先化简,再求值:
[(x+2y)2﹣(x﹣3y)(x+y)]÷(3y),其中x=5,y=2.
15.当 时,求 的值.
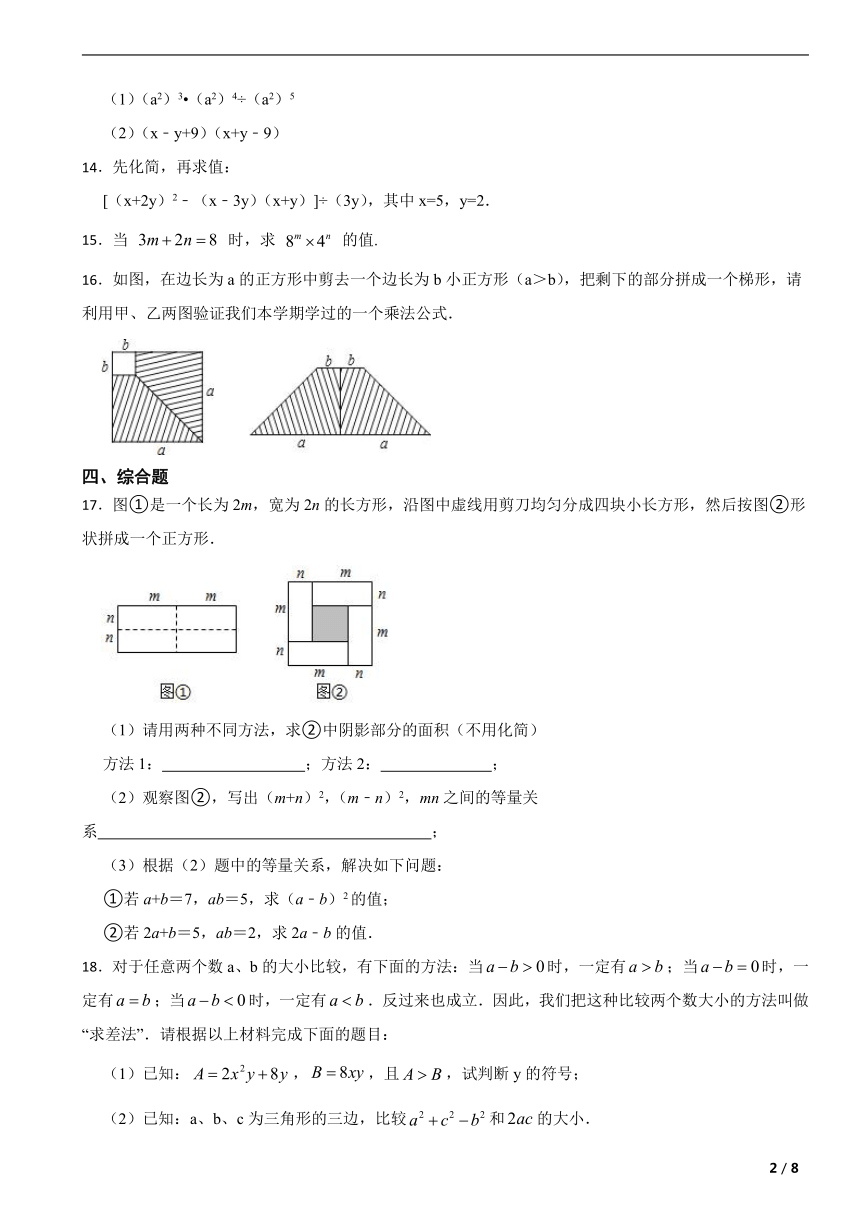
16.如图,在边长为a的正方形中剪去一个边长为b小正方形(a>b),把剩下的部分拼成一个梯形,请利用甲、乙两图验证我们本学期学过的一个乘法公式.
四、综合题
17.图①是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均匀分成四块小长方形,然后按图②形状拼成一个正方形.
(1)请用两种不同方法,求②中阴影部分的面积(不用化简)
方法1: ;方法2: ;
(2)观察图②,写出(m+n)2,(m﹣n)2,mn之间的等量关系 ;
(3)根据(2)题中的等量关系,解决如下问题:
①若a+b=7,ab=5,求(a﹣b)2的值;
②若2a+b=5,ab=2,求2a﹣b的值.
18.对于任意两个数a、b的大小比较,有下面的方法:当时,一定有;当时,一定有;当时,一定有.反过来也成立.因此,我们把这种比较两个数大小的方法叫做“求差法”.请根据以上材料完成下面的题目:
(1)已知:,,且,试判断y的符号;
(2)已知:a、b、c为三角形的三边,比较和的大小.
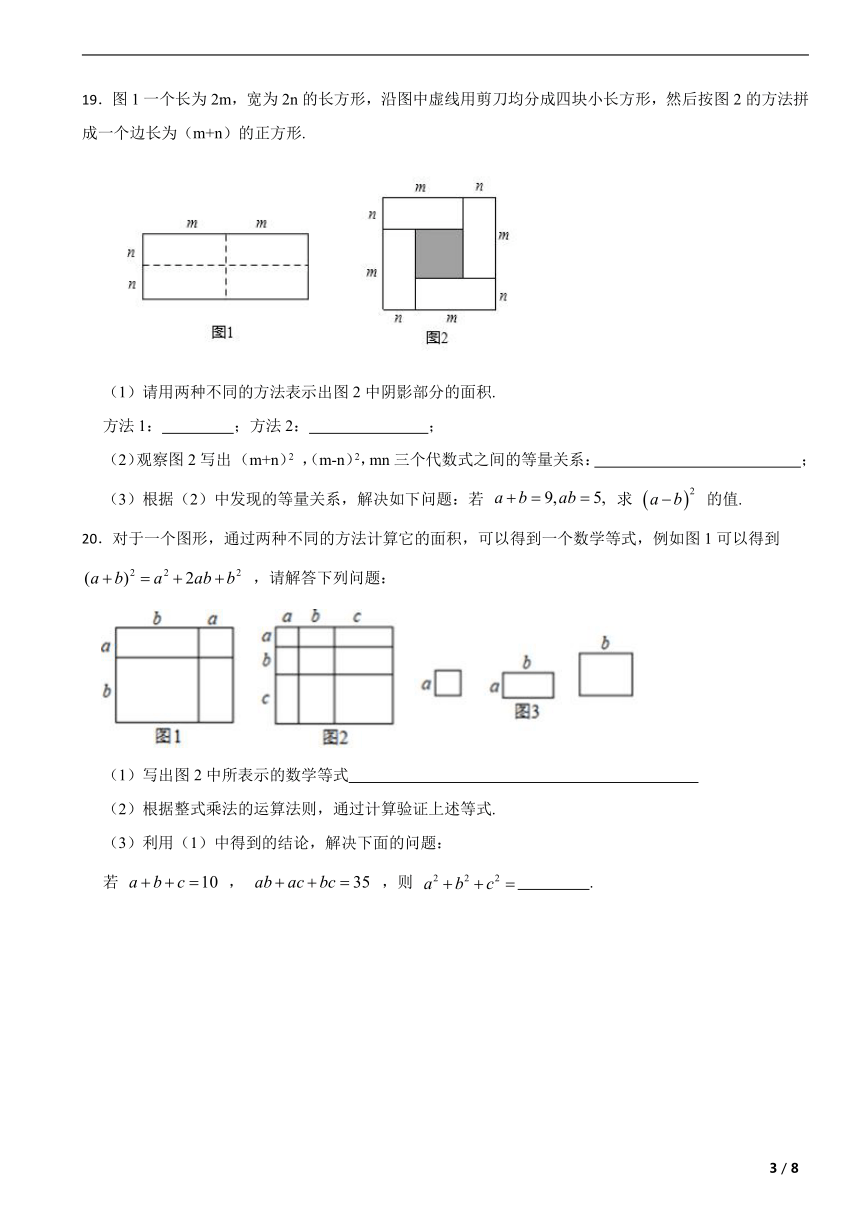
19.图1一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的方法拼成一个边长为(m+n)的正方形.
(1)请用两种不同的方法表示出图2中阴影部分的面积.
方法1: ;方法2: ;
(2)观察图2写出 (m+n)2 ,(m-n)2,mn三个代数式之间的等量关系: ;
(3)根据(2)中发现的等量关系,解决如下问题:若 求 的值.
20.对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式,例如图1可以得到 ,请解答下列问题:
(1)写出图2中所表示的数学等式
(2)根据整式乘法的运算法则,通过计算验证上述等式.
(3)利用(1)中得到的结论,解决下面的问题:
若 , ,则 .
答案解析部分
1.【答案】B
2.【答案】C
3.【答案】D
4.【答案】B
5.【答案】B
6.【答案】B
7.【答案】B
8.【答案】D
9.【答案】3
10.【答案】
11.【答案】4
12.【答案】-31
13.【答案】解:(1)原式=a6 a8÷a10
=a6+8﹣10
=a4;
(2)原式0=[x﹣(y﹣9)][(x+(y﹣9)]
=x2﹣(y﹣9)2
=x2﹣y2+18y﹣81.
14.【答案】解:原式=[x2+2 x 2y+(2y)2﹣(x2+xy﹣3xy﹣3y2)]÷(3y)
=(x2+4xy+4y2﹣x2+2xy+3y2)÷(3y)
=(6xy+7y2)÷(3y)
=2x+ y
当x=5,y=2时,
原式=2×5+ ×2
=10+
=
15.【答案】解:
16.【答案】解:左图中阴影部分的面积是a2﹣b2,右图中梯形的面积是(2a+2b)(a﹣b)=(a+b)(a﹣b),
∵左右的阴影部分的面积相等,
∴a2﹣b2=(a+b)(a﹣b).
17.【答案】(1)(m+n)2﹣4mm;(m﹣n)2
(2)m2+2mn+n2﹣4mn=m2﹣2mn+n2=(m﹣n)2
(3)解:①(a﹣b)2=(a+b)2﹣4ab
=72﹣4×5
=49﹣20=29;
②(2a﹣b)2=(2a+b)2﹣8ab
=52﹣8×2
=25﹣16=9;
∴2a﹣b=±3;
18.【答案】(1)解:因为A>B,
所以A-B>0,
即 ,
∴ ,
因为 ,
∴y>0
(2)解:因为a2 b2+c2 2ac=a2+c2 2ac b2=(a c)2 b2=(a c b)(a c+b),
∵a+b>c,a<b+c,
所以(a c b)(a c+b)<0,
所以a2 b2+c2 2ac的符号为负.
∴ <
19.【答案】(1);
(2)(m-n)2=(m+n)2-4mn
(3)解:由题意得:(a-b)2=(a+b)2-4ab
将a+b=9,ab=5代入上式得:(a-b)2=92-4×5=61
答:(a-b)2的值是61.
20.【答案】(1)(a+b+c)2=a2+b2+c2+2ab+2ac+2bc
(2)(a+b+c)2
=(a+b+c)(a+b+c)
=a2+ab+ac+ba+b2+bc+ca+cb+c2
=a2+b2+c2+2ab+2ac+2bc;
所以(1)中的等式成立;
(3)30
试题分析部分
1、试卷总体分布分析
总分:77分
分值分布 客观题(占比) 20.0(26.0%)
主观题(占比) 57.0(74.0%)
题量分布 客观题(占比) 10(50.0%)
主观题(占比) 10(50.0%)
2、试卷题量分布分析
大题题型 题目量(占比) 分值(占比)
填空题 4(20.0%) 8.0(10.4%)
解答题 4(20.0%) 20.0(26.0%)
综合题 4(20.0%) 33.0(42.9%)
单选题 8(40.0%) 16.0(20.8%)
3、试卷难度结构分析
序号 难易度 占比
1 普通 (75.0%)
2 容易 (20.0%)
3 困难 (5.0%)
4、试卷知识点分析
序号 知识点(认知水平) 分值(占比) 对应题号
1 平方差公式及应用 2.0(2.6%) 4
2 同类项的概念 2.0(2.6%) 7
3 积的乘方 2.0(2.6%) 8
4 平方差公式的几何背景 5.0(6.5%) 16
5 单项式除以单项式 2.0(2.6%) 10
6 因式分解﹣提公因式法 6.0(7.8%) 2,5,12
7 完全平方公式的几何背景 23.0(29.9%) 17,19,20
8 因式分解的应用 10.0(13.0%) 18
9 单项式乘单项式 2.0(2.6%) 1
10 因式分解的定义 2.0(2.6%) 3
11 整式的混合运算 12.0(15.6%) 6,13,14
12 完全平方公式及运用 18.0(23.4%) 8,17,19
13 多项式乘多项式 7.0(9.1%) 20
14 多项式除以单项式 2.0(2.6%) 11
15 因式分解﹣分组分解法 2.0(2.6%) 5
16 同底数幂的除法 6.0(7.8%) 7,8,9
17 幂的乘方 7.0(9.1%) 7,15
18 同底数幂的乘法 9.0(11.7%) 7,8,15
1 / 1
一、单选题
1.计算 结果正确的是( )
A. B. C. D.
2.多项式分解因式时,应提取的公因式是( )
A. B. C. D.
3.下列等式从左到右的变形中,属于因式分解的是( )
A.ab+ac+d=a(b+c)+d B.(x+1)(x+3)=x2+4x+3
C.6ab=2a·3b D.x(x-y)+y(y-x)=(x-y)2
4.下列各式能用平方差公式进行分解因式的是( )
A.x2+1 B.﹣1+x2 C.﹣x2﹣y2 D.x2+4x+4
5.把多项式a3+2a2b+ab2﹣a分解因式正确的是( )
A.(a2+ab+a)(a+b+1) B.a(a+b+1)(a+b﹣1)
C.a(a2+2ab+b2﹣1) D.(a2+ab+a)(a2+ab﹣a)
6.若 , ,则M与N的大小关系是( )
A.M>N B.M
A.a2+2a3=3a5 B.a a2=a3
C.a6÷a2=a3 D.(a2)3=a5
8.下列运算正确的是( )
A.a2 a3=a6 B.a3÷a﹣3=1
C.(a﹣b)2=a2﹣ab+b2 D.(﹣a2)3=﹣a6
二、填空题
9.若am=9,an=3,则am-n= .
10.计算: .
11.若m-n=2,则(2m2n-2mn2)÷(mn)的值为 .
12.已知(2x-21)(3x-7)-(3x-7)(x-13)可分解因式为(3x+a)(x+b),其中a,b均为整数,则a+3b= 。
三、解答题
13.计算题:
(1)(a2)3 (a2)4÷(a2)5
(2)(x﹣y+9)(x+y﹣9)
14.先化简,再求值:
[(x+2y)2﹣(x﹣3y)(x+y)]÷(3y),其中x=5,y=2.
15.当 时,求 的值.
16.如图,在边长为a的正方形中剪去一个边长为b小正方形(a>b),把剩下的部分拼成一个梯形,请利用甲、乙两图验证我们本学期学过的一个乘法公式.
四、综合题
17.图①是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均匀分成四块小长方形,然后按图②形状拼成一个正方形.
(1)请用两种不同方法,求②中阴影部分的面积(不用化简)
方法1: ;方法2: ;
(2)观察图②,写出(m+n)2,(m﹣n)2,mn之间的等量关系 ;
(3)根据(2)题中的等量关系,解决如下问题:
①若a+b=7,ab=5,求(a﹣b)2的值;
②若2a+b=5,ab=2,求2a﹣b的值.
18.对于任意两个数a、b的大小比较,有下面的方法:当时,一定有;当时,一定有;当时,一定有.反过来也成立.因此,我们把这种比较两个数大小的方法叫做“求差法”.请根据以上材料完成下面的题目:
(1)已知:,,且,试判断y的符号;
(2)已知:a、b、c为三角形的三边,比较和的大小.
19.图1一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的方法拼成一个边长为(m+n)的正方形.
(1)请用两种不同的方法表示出图2中阴影部分的面积.
方法1: ;方法2: ;
(2)观察图2写出 (m+n)2 ,(m-n)2,mn三个代数式之间的等量关系: ;
(3)根据(2)中发现的等量关系,解决如下问题:若 求 的值.
20.对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式,例如图1可以得到 ,请解答下列问题:
(1)写出图2中所表示的数学等式
(2)根据整式乘法的运算法则,通过计算验证上述等式.
(3)利用(1)中得到的结论,解决下面的问题:
若 , ,则 .
答案解析部分
1.【答案】B
2.【答案】C
3.【答案】D
4.【答案】B
5.【答案】B
6.【答案】B
7.【答案】B
8.【答案】D
9.【答案】3
10.【答案】
11.【答案】4
12.【答案】-31
13.【答案】解:(1)原式=a6 a8÷a10
=a6+8﹣10
=a4;
(2)原式0=[x﹣(y﹣9)][(x+(y﹣9)]
=x2﹣(y﹣9)2
=x2﹣y2+18y﹣81.
14.【答案】解:原式=[x2+2 x 2y+(2y)2﹣(x2+xy﹣3xy﹣3y2)]÷(3y)
=(x2+4xy+4y2﹣x2+2xy+3y2)÷(3y)
=(6xy+7y2)÷(3y)
=2x+ y
当x=5,y=2时,
原式=2×5+ ×2
=10+
=
15.【答案】解:
16.【答案】解:左图中阴影部分的面积是a2﹣b2,右图中梯形的面积是(2a+2b)(a﹣b)=(a+b)(a﹣b),
∵左右的阴影部分的面积相等,
∴a2﹣b2=(a+b)(a﹣b).
17.【答案】(1)(m+n)2﹣4mm;(m﹣n)2
(2)m2+2mn+n2﹣4mn=m2﹣2mn+n2=(m﹣n)2
(3)解:①(a﹣b)2=(a+b)2﹣4ab
=72﹣4×5
=49﹣20=29;
②(2a﹣b)2=(2a+b)2﹣8ab
=52﹣8×2
=25﹣16=9;
∴2a﹣b=±3;
18.【答案】(1)解:因为A>B,
所以A-B>0,
即 ,
∴ ,
因为 ,
∴y>0
(2)解:因为a2 b2+c2 2ac=a2+c2 2ac b2=(a c)2 b2=(a c b)(a c+b),
∵a+b>c,a<b+c,
所以(a c b)(a c+b)<0,
所以a2 b2+c2 2ac的符号为负.
∴ <
19.【答案】(1);
(2)(m-n)2=(m+n)2-4mn
(3)解:由题意得:(a-b)2=(a+b)2-4ab
将a+b=9,ab=5代入上式得:(a-b)2=92-4×5=61
答:(a-b)2的值是61.
20.【答案】(1)(a+b+c)2=a2+b2+c2+2ab+2ac+2bc
(2)(a+b+c)2
=(a+b+c)(a+b+c)
=a2+ab+ac+ba+b2+bc+ca+cb+c2
=a2+b2+c2+2ab+2ac+2bc;
所以(1)中的等式成立;
(3)30
试题分析部分
1、试卷总体分布分析
总分:77分
分值分布 客观题(占比) 20.0(26.0%)
主观题(占比) 57.0(74.0%)
题量分布 客观题(占比) 10(50.0%)
主观题(占比) 10(50.0%)
2、试卷题量分布分析
大题题型 题目量(占比) 分值(占比)
填空题 4(20.0%) 8.0(10.4%)
解答题 4(20.0%) 20.0(26.0%)
综合题 4(20.0%) 33.0(42.9%)
单选题 8(40.0%) 16.0(20.8%)
3、试卷难度结构分析
序号 难易度 占比
1 普通 (75.0%)
2 容易 (20.0%)
3 困难 (5.0%)
4、试卷知识点分析
序号 知识点(认知水平) 分值(占比) 对应题号
1 平方差公式及应用 2.0(2.6%) 4
2 同类项的概念 2.0(2.6%) 7
3 积的乘方 2.0(2.6%) 8
4 平方差公式的几何背景 5.0(6.5%) 16
5 单项式除以单项式 2.0(2.6%) 10
6 因式分解﹣提公因式法 6.0(7.8%) 2,5,12
7 完全平方公式的几何背景 23.0(29.9%) 17,19,20
8 因式分解的应用 10.0(13.0%) 18
9 单项式乘单项式 2.0(2.6%) 1
10 因式分解的定义 2.0(2.6%) 3
11 整式的混合运算 12.0(15.6%) 6,13,14
12 完全平方公式及运用 18.0(23.4%) 8,17,19
13 多项式乘多项式 7.0(9.1%) 20
14 多项式除以单项式 2.0(2.6%) 11
15 因式分解﹣分组分解法 2.0(2.6%) 5
16 同底数幂的除法 6.0(7.8%) 7,8,9
17 幂的乘方 7.0(9.1%) 7,15
18 同底数幂的乘法 9.0(11.7%) 7,8,15
1 / 1
