人教版八年级数学上册第十三章轴对称单元复习题(含解析)
文档属性
| 名称 | 人教版八年级数学上册第十三章轴对称单元复习题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 264.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-18 15:01:25 | ||
图片预览



文档简介
人教版八年级数学上册第十三章轴对称单元复习题
一、单选题
1.点M(3,2)关于y轴的对称点的坐标为( )
A.(﹣3,2) B.(3,﹣2)
C.(﹣3,﹣2) D.(1,2)
2. 国家宝藏 节目立足于中华文化宝库资源,通过对文物的梳理与总结,演绎文物背后的故事与历史,让更多观众走进博物馆,让一个个馆藏文物鲜活起来 下面四幅图是我国一些博物馆的标志,其中是轴对称图形的是
A. B. C. D.
3.垃圾分类引领着低碳生活新时尚,其目的是提高垃圾的资源价值和经济价值,力争物尽其用.在下列垃圾分类的标识标志中,不能看作轴对称图形的是( )
A. B. C. D.
4.如图,在△ABC中,BC边上的垂直平分线DE与边BC交于点D,边AB交于点E.若△EDC的周长为24,△ABC与四边形AEDC的周长之差为12,则线段DE的长为( )
A.12 B.6 C.24 D.36
5.如图,△ABC中,∠C=90°,AC=3,∠B=30°,点P是BC边上的动点,则AP长不可能是( )
A.3.5 B.4.2 C.5.8 D.7
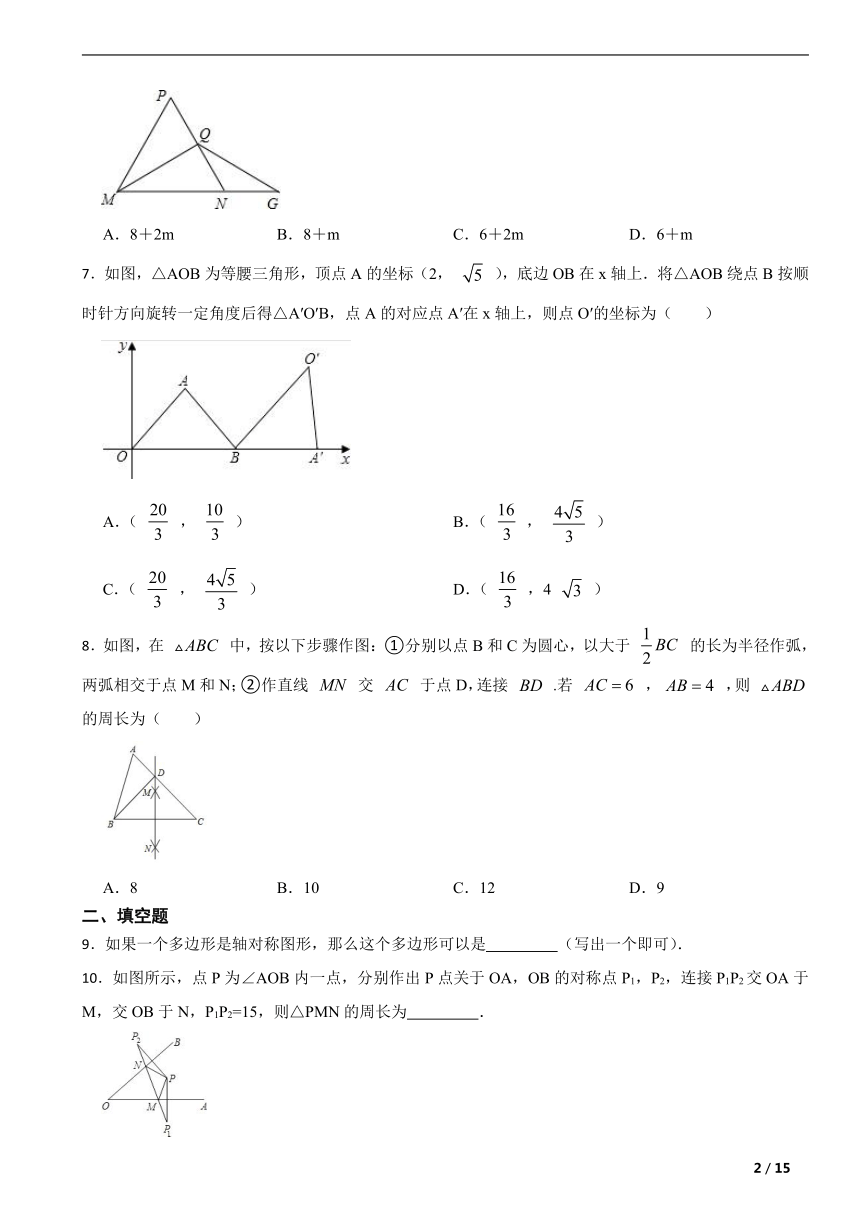
6.如图, 中, , , ,垂足为Q,延长MN至G,取 ,若 的周长为12, ,则 周长是( )
A.8+2m B.8+m C.6+2m D.6+m
7.如图,△AOB为等腰三角形,顶点A的坐标(2, ),底边OB在x轴上.将△AOB绕点B按顺时针方向旋转一定角度后得△A′O′B,点A的对应点A′在x轴上,则点O′的坐标为( )
A.( , ) B.( , )
C.( , ) D.( ,4 )
8.如图,在 中,按以下步骤作图:①分别以点B和C为圆心,以大于 的长为半径作弧,两弧相交于点M和N;②作直线 交 于点D,连接 .若 , ,则 的周长为( )
A.8 B.10 C.12 D.9
二、填空题
9.如果一个多边形是轴对称图形,那么这个多边形可以是 (写出一个即可).
10.如图所示,点P为∠AOB内一点,分别作出P点关于OA,OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,P1P2=15,则△PMN的周长为 .
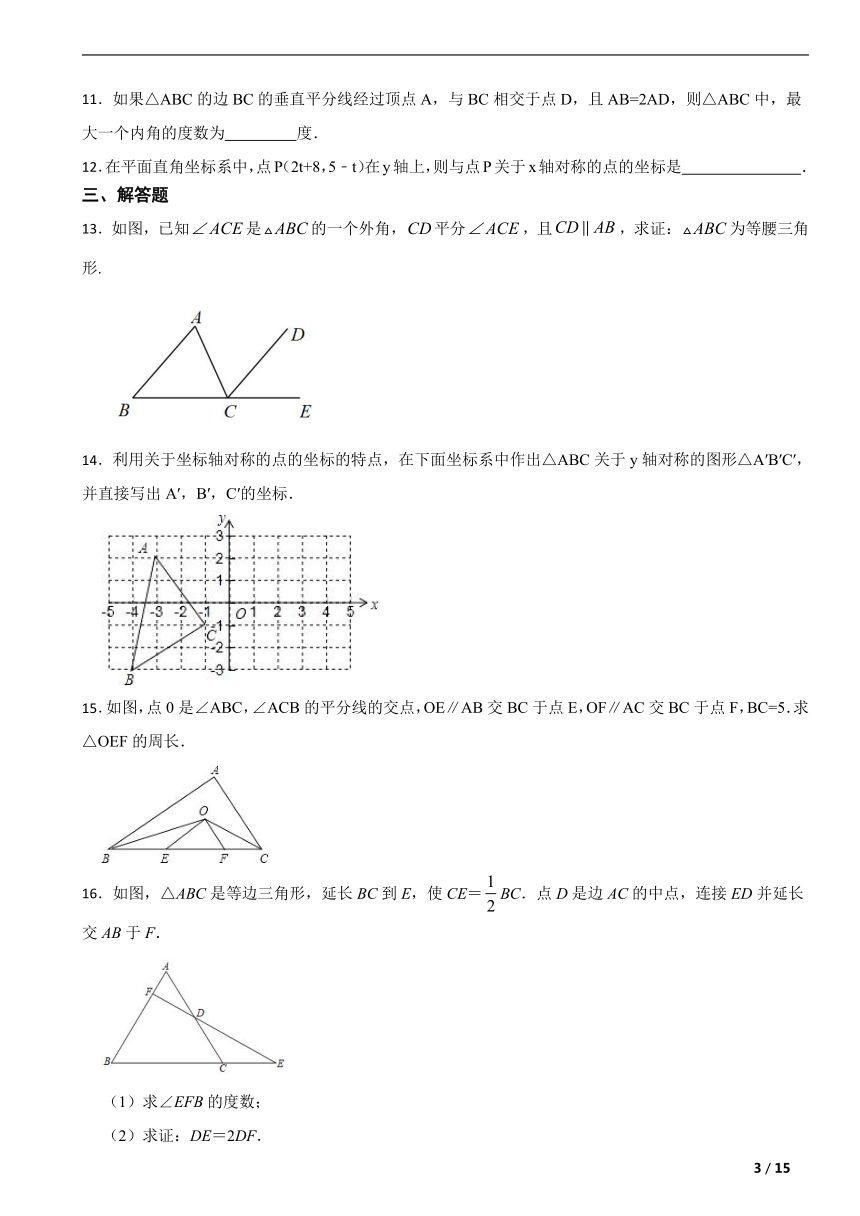
11.如果△ABC的边BC的垂直平分线经过顶点A,与BC相交于点D,且AB=2AD,则△ABC中,最大一个内角的度数为 度.
12.在平面直角坐标系中,点P(2t+8,5﹣t)在y轴上,则与点P关于x轴对称的点的坐标是 .
三、解答题
13.如图,已知是的一个外角,平分,且,求证:为等腰三角形.
14.利用关于坐标轴对称的点的坐标的特点,在下面坐标系中作出△ABC关于y轴对称的图形△A′B′C′,并直接写出A′,B′,C′的坐标.
15.如图,点0是∠ABC,∠ACB的平分线的交点,OE∥AB交BC于点E,OF∥AC交BC于点F,BC=5.求△OEF的周长.
16.如图,△ABC是等边三角形,延长BC到E,使CE=BC.点D是边AC的中点,连接ED并延长交AB于F.
(1)求∠EFB的度数;
(2)求证:DE=2DF.
四、综合题
17.如图,在△ABC中,点D,E分别在AB,AC上.
(1)若BD=CE,CD=BE,求证AB=AC;
(2)分别将“BD=CE”记为①,“CD=BE”记为②,“AB=AC”记为③.以①、③为条件,②为结论构成命题1,以②、③为条件,①为结论构成命题2.则命题1是 命题,命题2是 命题(选择“真”或“假“填入空格)
18.如图,已知:AC=BC,AC⊥BC,AE⊥CF,BF⊥CF,C、E、F分别为垂足, 且∠BCF=∠ABF,CF交AB于D.
(1)判断△BCF≌△CAE,并说明理由.
(2)判断△ADC是不是等腰三角形?并说明理由.
19.如图,在 中, ,点 在 延长线上, 于点 ,交 于点 .
(1)求证: .
(2)若 , ,求 的长.
20.如图,△ABC是等边三角形,D是边BC上(除B,C外)的任意一点,∠ADE=60°,且DE交∠ACF的平分线CE于点E.求证:
(1)∠1=∠2;
(2)AD=DE.
21.已知等边三角形ABC中,E是AB边上一动点(与A、B不重合),D是CB延长线上的一点,且DE=EC.
(1)当E是AB边上中点时,如图1,线段AE与DB的大小关系是:AE DB(填“>”,“<”或“=”)
(2)当E是AB边上任一点时,小敏与同桌小聪讨论后,认为(1)中的结论依然成立,并进行了如下解答:解:如图2,过点E作EF∥BC,交AC于点F
(请你按照上述思路,补充完成全部解答过程)
(3)当E是线段AB延长线上任一点时,如图3.(1)中的结论是否依然成立?若成立,请证明.若不成立,请说明理由.
答案解析部分
1.【答案】A
【解析】【解答】解:点(3,2)关于y轴的对称点的坐标是(-3,2).
故答案为:A.
【分析】根据关于y轴对称的特征:横坐标变为相反数,纵坐标不变即可得到答案。
2.【答案】A
【解析】【解答】解:A、此图案是轴对称图形,故A符合题意;
B、此图案不是轴对称图形,故B不符合题意;
C、此图案不是轴对称图形,故C不符合题意;
D、此图案不是轴对称图形,故D不符合题意;
故答案为:A
【分析】轴对称图形是把一个图形沿着一条直线折叠,直线两旁的部分能够完全重合,再对各选项逐一判断,可得答案。
3.【答案】D
【解析】【解答】A.是轴对称图形,不符合题意;
B.是轴对称图形,不符合题意;
C.是轴对称图形,不符合题意;
D.找不到对称轴,不是轴对称图形,符合题意;
【分析】轴对称图形:一个图形沿一条直线折叠,直线两旁的部分能够完全重合的图形,据此逐一判断即可.
4.【答案】B
【解析】【解答】∵DE是BC边上的垂直平分线,∴BE=CE,∵△EDC的周长为24,△ABC与四边形AEDC的周长之差为12,∴ED+DC+EC=24①,BE+BD-DE=12②,由①-②得,DE=6.故选B.
【分析】运用线段垂直平分线定理进行线段转换,根据题意列关系式后求解.
5.【答案】D
【解析】【解答】解:根据垂线段最短,可知AP的长不可小于3;
∵△ABC中,∠C=90°,AC=3,∠B=30°,
∴AB=6,
∴AP的长不能大于6.
故选:D.
【分析】利用垂线段最短分析AP最小不能小于3;利用含30度角的直角三角形的性质得出AB=6,可知AP最大不能大于6.此题可解.
6.【答案】C
【解析】【解答】解:∵ ,
,
∴△PMN是等边三角形,
∵ ,
∴QN=PQ=
,∠QMN=30°,∠QNM=60°,
∵ ,
∴∠GQN=∠G=30°,QN=NG=
,
∴∠QMN=∠G=30°,
∴QM=QG,
∵ 的周长为12,
,
∴MN=4,QN=NC=2,QM=QG=m,
∴ 周长是QM+QG+MN+NG=6+2m.
故答案为:C.
【分析】易得△PMN是等边三角形,得QN=PQ=
MN,∠QMN=30°,∠QNM=60°,根据等腰三角形的性质可得∠GQN=∠G=30°,QN=NG=
MN,推出QM=QG,根据△MNP的周长可得MN=4,QN=NC=2,QM=QG=m,据此求解.
7.【答案】C
【解析】【解答】解:如图,过点A作AC⊥OB于C,过点O′作O′D⊥A′B于D,
∵A(2, ),
∴OC=2,AC= ,
由勾股定理得,OA= = =3,
∵△AOB为等腰三角形,OB是底边,
∴OB=2OC=2×2=4,
由旋转的性质得,BO′=OB=4,∠A′BO′=∠ABO,
∴O′D=4× = ,
BD=4× = ,
∴OD=OB+BD=4+ = ,
∴点O′的坐标为( , ).
故选:C.
【分析】过点A作AC⊥OB于C,过点O′作O′D⊥A′B于D,根据点A的坐标求出OC、AC,再利用勾股定理列式计算求出OA,根据等腰三角形三线合一的性质求出OB,根据旋转的性质可得BO′=OB,∠A′BO′=∠ABO,然后解直角三角形求出O′D、BD,再求出OD,然后写出点O′的坐标即可.
8.【答案】B
【解析】【解答】解:由作图知,MN是线段BC的垂直平分线,
∴BD=CD,
∴AD+BD=AD+CD=AC=6
∵AB=4,
∴ 的周长=AB+BD+AD=AB+AC=4+6=10,
故答案为:B.
【分析】利用基本作图可判定MN是线段BC的垂直平分线,则BD=CD,然后利用等线段代换得到△ABD的周长=AB+AC,再把数值代入计算即可得出结果.
9.【答案】正方形
【解析】【解答】解:如果一个多边形是轴对称图形,那么这个多边形可以是:答案不唯一.如:正方形.
故答案为:答案不唯一.如:正方形.
【分析】根据轴对称的概念进行回答即可.
10.【答案】15
【解析】【解答】解:∵P点关于OA的对称是点P1,P点关于OB的对称点P2,
∴PM=P1M,PN=P2N.
∴△PMN的周长为PM+PN+MN=MN+P1M+P2N=P1P2=15.
故答案为:15
【分析】P点关于OA的对称是点P1,P点关于OB的对称点P2,故有PM=P1M,PN=P2N.
11.【答案】120
【解析】【解答】解:如图:
∵sinB= = ,∴∠B=30°.
∵AD垂直且平分BC,∴∠B=∠C=30°.
∴∠BAC=180°﹣∠B﹣∠C=180°﹣30°﹣30°=120°.
【分析】根据三角函数和三角形内角和定理解答.
12.【答案】(0,﹣9)
【解析】【解答】由题意,得
2t+8=0,
解得t=﹣4,
P(0,9)关于x轴对称的点的坐标是(0,﹣9),
故答案为:(0,﹣9).
【分析】关于x轴对称的点坐标特征为横同纵反.
13.【答案】证明:平分,
,
,
,,
,
,
为等腰三角形.
【解析】【分析】根据角平分线的定义得∠ACD=∠ECD,再根据平行线的性质得∠A=∠ACD,∠B=∠ECD,故∠A=∠B,根据等角对等边得AC=BC,从而根据等腰三角形的定义得出结论.
14.【答案】解:如图所示,△A′B′C′即为所求,
故A′(3,2),B′(4,﹣3),C′(1,﹣1)
【解析】【分析】依据轴对称的性质,作出△ABC各顶点关于y轴对称的点,再顺次连接即可;依据A′,B′,C′的位置即可得到A′,B′,C′的坐标.
15.【答案】解:∵OB,OC分别是∠ABC,∠ACB的平分线,
∴∠1=∠2,∠4=∠5,
∵OE∥AB,OF∥AC,
∴∠1=∠3,∠4=∠6,
∴∠2=∠3,∠5=∠6,
∴BE=OE,OF=FC,
∴BC=BE+EF+FC=OF+OE+EF,
∵BC=5,
∴OF+OE+EF=5
∴△OEF的周长=OF+OE+EF=5.
【解析】【分析】由OB,OC分别是△ABC的∠ABC和∠ACB的平分线和OE∥AB、OF∥AC可推出BE=OE,OF=FC,显然△OEF的周长即为BC的长度.
16.【答案】(1)解:∵△ABC是等边三角形,
∴AC=BC,∠ACB=∠B=60°,
∵点D是AC的中点,
∴CD=AC,
又∵CE=BC,
∴CE=CD,
∴∠CDE=∠E,
∵∠ACB=∠E+∠CDE=2∠E=60°,
∴∠E=30°,
∴∠BFE=180°-∠B-∠E=90°;
(2)证明:过点C作CM⊥DE于点M,
∵CD=CE,CM⊥EF,
∴DE=2DM,
在△ADF与△CDM中,
∵∠CMD=∠AFD=90°,∠ADF=∠CDM,AD=CD,
∴△ADF≌△CDM(AAS),
∴DM=DF,
∴DE=2DF.
【解析】【分析】(1)由等边三角形的性质得AC=BC,∠ACB=∠B=60°,由中点定义及已知可得CE=CD,由等边对等角得∠CDE=∠E,由三角形外角性质得∠ACB=∠E+∠CDE=2∠E=60°,则∠E=30°,最后根据三角形内角和定理可算出∠BFE的度数;
(2)过点C作CM⊥DE于点M,由等腰三角形的三线合一得DE=2DM,从而由AAS判断出△ADF≌△CDM,得DM=DF,从而即可得出结论.
17.【答案】(1)证明:∵BD=CE,CD=BE,BC=CB.
∴△DBC≌△ECB(SSS)
∴∠DBC=∠ECB
∴AB=AC.
(2)真;假
【解析】【解答】解:(2)命题1:已知BD=CE,AB=AC;求证:CD=BE;
证明:∵AB=AC,BD=CE,
∴AB-BD=AC-CE
∴AD=CE
在△ABE和△ACD,
∴△ABE≌△ACD
∴CD=BE.
则命题1为真命题;
命题2:已知CD=BE,AB=AC,求证:BD=CE;
∵CD=BE,AB=AC, 不是两边的夹角,无法证明△ABE≌△ACD,所以命题2为假命题.
故答案为:第一空、真;第二空、假.
【分析】(1)利用SSS易证△DBC≌△ECB,得到∠DBC=∠ECB,据此可得结论;
(2)命题1:已知BD=CE,AB=AC;求证:CD=BE;根据线段的和差关系可得AD=CE,利用SAS证明△ABE≌△ACD,据此可得结论;命题2:已知CD=BE,AB=AC,求证:BD=CE;无法证明△ABE≌△ACD,据此解答.
18.【答案】(1)解:△BCF≌△CAE.理由如下:
∵AC⊥BC,AE⊥CF,
∴∠ACE+∠BCF=90°,∠ACE+∠CAE=90°,
∴∠CAE=∠BCF,
∵AE⊥CF,BF⊥CF,
∴∠AEC=∠F=90°,
在△BCF和△CAE中,
∵ ,
∴△BCF≌△CAE(AAS)
(2)解:△ADC是等腰三角形.理由如下:
∵AC⊥BC,BF⊥CF,
∴∠ACB=∠F=90°,
∴∠ACD+∠BCF=90°,∠BDF+∠ABF=90°,
∵∠BCF=∠ABF,
∴∠ACD=∠BDF,
又∵∠BDF=∠ADC(对顶角相等),
∴∠ACD=∠ADC,
∴AC=AD,
故△ADC是等腰三角形
【解析】【分析】(1)△BCF≌△CAE.理由如下:根据同角的余角相等得出∠CAE=∠BCF,根据垂直的定义得出∠AEC=∠F=90°,然后利用AAS判断出△BCF≌△CAE;
(2)△ADC是等腰三角形.理由如下:根据垂直的定义得出∠ACB=∠F=90°,根据等角的余角相等得出∠ACD=∠BDF,根据对顶角相等得出∠BDF=∠ADC,故∠ACD=∠ADC,根据等腰三角形的判定即可得出△ADC是等腰三角形。
19.【答案】(1)证明:∵ ,∴ ,∵ ,
∴,∴ ,∠C+∠E=90°
∴ ,
又∵ ,
∴
(2)解:∵ ,∴ ,∴ 是等腰三角形,
又∵ , ,
∴ , ,
∴ .
【解析】【分析】(1)根据等边对等角得出∠B=∠C ,根据直角三角形的两锐角互余得出∠B+∠BFP=90° ,∠C+∠E=90°,根据等角的余角相等得出∠E=∠BFP ,根据对顶角相等及等量代换得出∠E=∠AFE;
(2)根据等角对等边得出AF=AE=3,根据线段的和差得出CA=AB=8 ,进而得出CE的长。
20.【答案】(1)证明:∵△ABC是等边三角形,∠ADE=60°,∴∠ADE=∠B=60°.
又∵∠ADC=∠2+∠ADE=∠1+∠B,∴∠1=∠2
(2)证明:如图,在AB上取一点M,使BM=BD,连接MD.∵△ABC是等边三角形,∴∠B=60°.
∴△BMD是等边三角形,∴∠BMD=60°,∴∠AMD=120°.
∵CE是∠ACF的平分线,
∴∠ECA=60°,∴∠DCE=120°.
∴∠AMD=∠DCE=120°,∵ AB=BC ,BM=BD,
∵BA-BM=BC-BD,
∴MA=CD.
在△AMD和△DCE中,
∴△AMD≌△DCE(ASA).
∴AD=DE 。
【解析】【分析】 (1)根据等边三角形的性质及已知得出∠ADE=∠B=60°,根据三角形的外角定理及角的和差得出∠ADC=∠2+∠ADE=∠1+∠B,从而得出∠1=∠2 ;
(2)根据等边三角形的性质得出∠B=60°,根据有一个角为60°的等腰三角形是等边三角形得出△BMD是等边三角形 ,等边三角形三个内角都是60°及邻补角的定义得出∠AMD=120°,根据角平分线的定义及角的和差得出∠DCE=120°,从而得出∠AMD=∠DCE=120°,根据等式的性质得出MA=CD,从而利用ASA判断出△AMD≌△DCE,利用全等三角形对应边相等得出AD=DE。
21.【答案】(1)=
(2)解:∵EF∥BC,
∴△AEF是等边三角形,
∴AB﹣AE=AC﹣AF,即BE=CF,
∵∠ABC=∠EDB+∠BED=60°,∠ACB=∠ECB+∠FCE=60°,
∵DE=EC,
∴∠EDB=∠ECB,
∴∠BED=∠FCE,
在△DBE和△EFC中,
,
∴△DBE≌△EFC,
∴DB=EF=AE;
(3)解:如图3,作EF∥AC交BD于F,
则△BEF为等边三角形,
∴∠EFB=∠EBF=60°,
∴∠EFD=∠EBC=120°,
∵DE=EC,
∴∠EDB=∠ECB,
在△DEF和△CEB中,
,
∴△DEF≌△CEB,
∴DF=BC,
∴DF+FB=AB+BE,
∴BD=AE.
【解析】【解答】解:(1)∵△ABC是等边三角形,E是AB边上中点,
∴AE=BE,∠BCE= ∠BCA=30°,
∵DE=EC,
∴∠EDB=∠ECB=30°,
∵∠ABC=60°,
∴∠BED=30°,
∴∠EDB=∠BED,
∴BD=BE,
∴BD=AE,
故答案为:=;
【分析】(1)根据等边三角形的性质、等腰三角形的三线合一证明;(2)证明△DBE≌△EFC,根据全等三角形的性质证明;(3)作EF∥AC交BD于F,证明△DEF≌△CEB,根据全等三角形的性质证明即可.
1 / 1
一、单选题
1.点M(3,2)关于y轴的对称点的坐标为( )
A.(﹣3,2) B.(3,﹣2)
C.(﹣3,﹣2) D.(1,2)
2. 国家宝藏 节目立足于中华文化宝库资源,通过对文物的梳理与总结,演绎文物背后的故事与历史,让更多观众走进博物馆,让一个个馆藏文物鲜活起来 下面四幅图是我国一些博物馆的标志,其中是轴对称图形的是
A. B. C. D.
3.垃圾分类引领着低碳生活新时尚,其目的是提高垃圾的资源价值和经济价值,力争物尽其用.在下列垃圾分类的标识标志中,不能看作轴对称图形的是( )
A. B. C. D.
4.如图,在△ABC中,BC边上的垂直平分线DE与边BC交于点D,边AB交于点E.若△EDC的周长为24,△ABC与四边形AEDC的周长之差为12,则线段DE的长为( )
A.12 B.6 C.24 D.36
5.如图,△ABC中,∠C=90°,AC=3,∠B=30°,点P是BC边上的动点,则AP长不可能是( )
A.3.5 B.4.2 C.5.8 D.7
6.如图, 中, , , ,垂足为Q,延长MN至G,取 ,若 的周长为12, ,则 周长是( )
A.8+2m B.8+m C.6+2m D.6+m
7.如图,△AOB为等腰三角形,顶点A的坐标(2, ),底边OB在x轴上.将△AOB绕点B按顺时针方向旋转一定角度后得△A′O′B,点A的对应点A′在x轴上,则点O′的坐标为( )
A.( , ) B.( , )
C.( , ) D.( ,4 )
8.如图,在 中,按以下步骤作图:①分别以点B和C为圆心,以大于 的长为半径作弧,两弧相交于点M和N;②作直线 交 于点D,连接 .若 , ,则 的周长为( )
A.8 B.10 C.12 D.9
二、填空题
9.如果一个多边形是轴对称图形,那么这个多边形可以是 (写出一个即可).
10.如图所示,点P为∠AOB内一点,分别作出P点关于OA,OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,P1P2=15,则△PMN的周长为 .
11.如果△ABC的边BC的垂直平分线经过顶点A,与BC相交于点D,且AB=2AD,则△ABC中,最大一个内角的度数为 度.
12.在平面直角坐标系中,点P(2t+8,5﹣t)在y轴上,则与点P关于x轴对称的点的坐标是 .
三、解答题
13.如图,已知是的一个外角,平分,且,求证:为等腰三角形.
14.利用关于坐标轴对称的点的坐标的特点,在下面坐标系中作出△ABC关于y轴对称的图形△A′B′C′,并直接写出A′,B′,C′的坐标.
15.如图,点0是∠ABC,∠ACB的平分线的交点,OE∥AB交BC于点E,OF∥AC交BC于点F,BC=5.求△OEF的周长.
16.如图,△ABC是等边三角形,延长BC到E,使CE=BC.点D是边AC的中点,连接ED并延长交AB于F.
(1)求∠EFB的度数;
(2)求证:DE=2DF.
四、综合题
17.如图,在△ABC中,点D,E分别在AB,AC上.
(1)若BD=CE,CD=BE,求证AB=AC;
(2)分别将“BD=CE”记为①,“CD=BE”记为②,“AB=AC”记为③.以①、③为条件,②为结论构成命题1,以②、③为条件,①为结论构成命题2.则命题1是 命题,命题2是 命题(选择“真”或“假“填入空格)
18.如图,已知:AC=BC,AC⊥BC,AE⊥CF,BF⊥CF,C、E、F分别为垂足, 且∠BCF=∠ABF,CF交AB于D.
(1)判断△BCF≌△CAE,并说明理由.
(2)判断△ADC是不是等腰三角形?并说明理由.
19.如图,在 中, ,点 在 延长线上, 于点 ,交 于点 .
(1)求证: .
(2)若 , ,求 的长.
20.如图,△ABC是等边三角形,D是边BC上(除B,C外)的任意一点,∠ADE=60°,且DE交∠ACF的平分线CE于点E.求证:
(1)∠1=∠2;
(2)AD=DE.
21.已知等边三角形ABC中,E是AB边上一动点(与A、B不重合),D是CB延长线上的一点,且DE=EC.
(1)当E是AB边上中点时,如图1,线段AE与DB的大小关系是:AE DB(填“>”,“<”或“=”)
(2)当E是AB边上任一点时,小敏与同桌小聪讨论后,认为(1)中的结论依然成立,并进行了如下解答:解:如图2,过点E作EF∥BC,交AC于点F
(请你按照上述思路,补充完成全部解答过程)
(3)当E是线段AB延长线上任一点时,如图3.(1)中的结论是否依然成立?若成立,请证明.若不成立,请说明理由.
答案解析部分
1.【答案】A
【解析】【解答】解:点(3,2)关于y轴的对称点的坐标是(-3,2).
故答案为:A.
【分析】根据关于y轴对称的特征:横坐标变为相反数,纵坐标不变即可得到答案。
2.【答案】A
【解析】【解答】解:A、此图案是轴对称图形,故A符合题意;
B、此图案不是轴对称图形,故B不符合题意;
C、此图案不是轴对称图形,故C不符合题意;
D、此图案不是轴对称图形,故D不符合题意;
故答案为:A
【分析】轴对称图形是把一个图形沿着一条直线折叠,直线两旁的部分能够完全重合,再对各选项逐一判断,可得答案。
3.【答案】D
【解析】【解答】A.是轴对称图形,不符合题意;
B.是轴对称图形,不符合题意;
C.是轴对称图形,不符合题意;
D.找不到对称轴,不是轴对称图形,符合题意;
【分析】轴对称图形:一个图形沿一条直线折叠,直线两旁的部分能够完全重合的图形,据此逐一判断即可.
4.【答案】B
【解析】【解答】∵DE是BC边上的垂直平分线,∴BE=CE,∵△EDC的周长为24,△ABC与四边形AEDC的周长之差为12,∴ED+DC+EC=24①,BE+BD-DE=12②,由①-②得,DE=6.故选B.
【分析】运用线段垂直平分线定理进行线段转换,根据题意列关系式后求解.
5.【答案】D
【解析】【解答】解:根据垂线段最短,可知AP的长不可小于3;
∵△ABC中,∠C=90°,AC=3,∠B=30°,
∴AB=6,
∴AP的长不能大于6.
故选:D.
【分析】利用垂线段最短分析AP最小不能小于3;利用含30度角的直角三角形的性质得出AB=6,可知AP最大不能大于6.此题可解.
6.【答案】C
【解析】【解答】解:∵ ,
,
∴△PMN是等边三角形,
∵ ,
∴QN=PQ=
,∠QMN=30°,∠QNM=60°,
∵ ,
∴∠GQN=∠G=30°,QN=NG=
,
∴∠QMN=∠G=30°,
∴QM=QG,
∵ 的周长为12,
,
∴MN=4,QN=NC=2,QM=QG=m,
∴ 周长是QM+QG+MN+NG=6+2m.
故答案为:C.
【分析】易得△PMN是等边三角形,得QN=PQ=
MN,∠QMN=30°,∠QNM=60°,根据等腰三角形的性质可得∠GQN=∠G=30°,QN=NG=
MN,推出QM=QG,根据△MNP的周长可得MN=4,QN=NC=2,QM=QG=m,据此求解.
7.【答案】C
【解析】【解答】解:如图,过点A作AC⊥OB于C,过点O′作O′D⊥A′B于D,
∵A(2, ),
∴OC=2,AC= ,
由勾股定理得,OA= = =3,
∵△AOB为等腰三角形,OB是底边,
∴OB=2OC=2×2=4,
由旋转的性质得,BO′=OB=4,∠A′BO′=∠ABO,
∴O′D=4× = ,
BD=4× = ,
∴OD=OB+BD=4+ = ,
∴点O′的坐标为( , ).
故选:C.
【分析】过点A作AC⊥OB于C,过点O′作O′D⊥A′B于D,根据点A的坐标求出OC、AC,再利用勾股定理列式计算求出OA,根据等腰三角形三线合一的性质求出OB,根据旋转的性质可得BO′=OB,∠A′BO′=∠ABO,然后解直角三角形求出O′D、BD,再求出OD,然后写出点O′的坐标即可.
8.【答案】B
【解析】【解答】解:由作图知,MN是线段BC的垂直平分线,
∴BD=CD,
∴AD+BD=AD+CD=AC=6
∵AB=4,
∴ 的周长=AB+BD+AD=AB+AC=4+6=10,
故答案为:B.
【分析】利用基本作图可判定MN是线段BC的垂直平分线,则BD=CD,然后利用等线段代换得到△ABD的周长=AB+AC,再把数值代入计算即可得出结果.
9.【答案】正方形
【解析】【解答】解:如果一个多边形是轴对称图形,那么这个多边形可以是:答案不唯一.如:正方形.
故答案为:答案不唯一.如:正方形.
【分析】根据轴对称的概念进行回答即可.
10.【答案】15
【解析】【解答】解:∵P点关于OA的对称是点P1,P点关于OB的对称点P2,
∴PM=P1M,PN=P2N.
∴△PMN的周长为PM+PN+MN=MN+P1M+P2N=P1P2=15.
故答案为:15
【分析】P点关于OA的对称是点P1,P点关于OB的对称点P2,故有PM=P1M,PN=P2N.
11.【答案】120
【解析】【解答】解:如图:
∵sinB= = ,∴∠B=30°.
∵AD垂直且平分BC,∴∠B=∠C=30°.
∴∠BAC=180°﹣∠B﹣∠C=180°﹣30°﹣30°=120°.
【分析】根据三角函数和三角形内角和定理解答.
12.【答案】(0,﹣9)
【解析】【解答】由题意,得
2t+8=0,
解得t=﹣4,
P(0,9)关于x轴对称的点的坐标是(0,﹣9),
故答案为:(0,﹣9).
【分析】关于x轴对称的点坐标特征为横同纵反.
13.【答案】证明:平分,
,
,
,,
,
,
为等腰三角形.
【解析】【分析】根据角平分线的定义得∠ACD=∠ECD,再根据平行线的性质得∠A=∠ACD,∠B=∠ECD,故∠A=∠B,根据等角对等边得AC=BC,从而根据等腰三角形的定义得出结论.
14.【答案】解:如图所示,△A′B′C′即为所求,
故A′(3,2),B′(4,﹣3),C′(1,﹣1)
【解析】【分析】依据轴对称的性质,作出△ABC各顶点关于y轴对称的点,再顺次连接即可;依据A′,B′,C′的位置即可得到A′,B′,C′的坐标.
15.【答案】解:∵OB,OC分别是∠ABC,∠ACB的平分线,
∴∠1=∠2,∠4=∠5,
∵OE∥AB,OF∥AC,
∴∠1=∠3,∠4=∠6,
∴∠2=∠3,∠5=∠6,
∴BE=OE,OF=FC,
∴BC=BE+EF+FC=OF+OE+EF,
∵BC=5,
∴OF+OE+EF=5
∴△OEF的周长=OF+OE+EF=5.
【解析】【分析】由OB,OC分别是△ABC的∠ABC和∠ACB的平分线和OE∥AB、OF∥AC可推出BE=OE,OF=FC,显然△OEF的周长即为BC的长度.
16.【答案】(1)解:∵△ABC是等边三角形,
∴AC=BC,∠ACB=∠B=60°,
∵点D是AC的中点,
∴CD=AC,
又∵CE=BC,
∴CE=CD,
∴∠CDE=∠E,
∵∠ACB=∠E+∠CDE=2∠E=60°,
∴∠E=30°,
∴∠BFE=180°-∠B-∠E=90°;
(2)证明:过点C作CM⊥DE于点M,
∵CD=CE,CM⊥EF,
∴DE=2DM,
在△ADF与△CDM中,
∵∠CMD=∠AFD=90°,∠ADF=∠CDM,AD=CD,
∴△ADF≌△CDM(AAS),
∴DM=DF,
∴DE=2DF.
【解析】【分析】(1)由等边三角形的性质得AC=BC,∠ACB=∠B=60°,由中点定义及已知可得CE=CD,由等边对等角得∠CDE=∠E,由三角形外角性质得∠ACB=∠E+∠CDE=2∠E=60°,则∠E=30°,最后根据三角形内角和定理可算出∠BFE的度数;
(2)过点C作CM⊥DE于点M,由等腰三角形的三线合一得DE=2DM,从而由AAS判断出△ADF≌△CDM,得DM=DF,从而即可得出结论.
17.【答案】(1)证明:∵BD=CE,CD=BE,BC=CB.
∴△DBC≌△ECB(SSS)
∴∠DBC=∠ECB
∴AB=AC.
(2)真;假
【解析】【解答】解:(2)命题1:已知BD=CE,AB=AC;求证:CD=BE;
证明:∵AB=AC,BD=CE,
∴AB-BD=AC-CE
∴AD=CE
在△ABE和△ACD,
∴△ABE≌△ACD
∴CD=BE.
则命题1为真命题;
命题2:已知CD=BE,AB=AC,求证:BD=CE;
∵CD=BE,AB=AC, 不是两边的夹角,无法证明△ABE≌△ACD,所以命题2为假命题.
故答案为:第一空、真;第二空、假.
【分析】(1)利用SSS易证△DBC≌△ECB,得到∠DBC=∠ECB,据此可得结论;
(2)命题1:已知BD=CE,AB=AC;求证:CD=BE;根据线段的和差关系可得AD=CE,利用SAS证明△ABE≌△ACD,据此可得结论;命题2:已知CD=BE,AB=AC,求证:BD=CE;无法证明△ABE≌△ACD,据此解答.
18.【答案】(1)解:△BCF≌△CAE.理由如下:
∵AC⊥BC,AE⊥CF,
∴∠ACE+∠BCF=90°,∠ACE+∠CAE=90°,
∴∠CAE=∠BCF,
∵AE⊥CF,BF⊥CF,
∴∠AEC=∠F=90°,
在△BCF和△CAE中,
∵ ,
∴△BCF≌△CAE(AAS)
(2)解:△ADC是等腰三角形.理由如下:
∵AC⊥BC,BF⊥CF,
∴∠ACB=∠F=90°,
∴∠ACD+∠BCF=90°,∠BDF+∠ABF=90°,
∵∠BCF=∠ABF,
∴∠ACD=∠BDF,
又∵∠BDF=∠ADC(对顶角相等),
∴∠ACD=∠ADC,
∴AC=AD,
故△ADC是等腰三角形
【解析】【分析】(1)△BCF≌△CAE.理由如下:根据同角的余角相等得出∠CAE=∠BCF,根据垂直的定义得出∠AEC=∠F=90°,然后利用AAS判断出△BCF≌△CAE;
(2)△ADC是等腰三角形.理由如下:根据垂直的定义得出∠ACB=∠F=90°,根据等角的余角相等得出∠ACD=∠BDF,根据对顶角相等得出∠BDF=∠ADC,故∠ACD=∠ADC,根据等腰三角形的判定即可得出△ADC是等腰三角形。
19.【答案】(1)证明:∵ ,∴ ,∵ ,
∴,∴ ,∠C+∠E=90°
∴ ,
又∵ ,
∴
(2)解:∵ ,∴ ,∴ 是等腰三角形,
又∵ , ,
∴ , ,
∴ .
【解析】【分析】(1)根据等边对等角得出∠B=∠C ,根据直角三角形的两锐角互余得出∠B+∠BFP=90° ,∠C+∠E=90°,根据等角的余角相等得出∠E=∠BFP ,根据对顶角相等及等量代换得出∠E=∠AFE;
(2)根据等角对等边得出AF=AE=3,根据线段的和差得出CA=AB=8 ,进而得出CE的长。
20.【答案】(1)证明:∵△ABC是等边三角形,∠ADE=60°,∴∠ADE=∠B=60°.
又∵∠ADC=∠2+∠ADE=∠1+∠B,∴∠1=∠2
(2)证明:如图,在AB上取一点M,使BM=BD,连接MD.∵△ABC是等边三角形,∴∠B=60°.
∴△BMD是等边三角形,∴∠BMD=60°,∴∠AMD=120°.
∵CE是∠ACF的平分线,
∴∠ECA=60°,∴∠DCE=120°.
∴∠AMD=∠DCE=120°,∵ AB=BC ,BM=BD,
∵BA-BM=BC-BD,
∴MA=CD.
在△AMD和△DCE中,
∴△AMD≌△DCE(ASA).
∴AD=DE 。
【解析】【分析】 (1)根据等边三角形的性质及已知得出∠ADE=∠B=60°,根据三角形的外角定理及角的和差得出∠ADC=∠2+∠ADE=∠1+∠B,从而得出∠1=∠2 ;
(2)根据等边三角形的性质得出∠B=60°,根据有一个角为60°的等腰三角形是等边三角形得出△BMD是等边三角形 ,等边三角形三个内角都是60°及邻补角的定义得出∠AMD=120°,根据角平分线的定义及角的和差得出∠DCE=120°,从而得出∠AMD=∠DCE=120°,根据等式的性质得出MA=CD,从而利用ASA判断出△AMD≌△DCE,利用全等三角形对应边相等得出AD=DE。
21.【答案】(1)=
(2)解:∵EF∥BC,
∴△AEF是等边三角形,
∴AB﹣AE=AC﹣AF,即BE=CF,
∵∠ABC=∠EDB+∠BED=60°,∠ACB=∠ECB+∠FCE=60°,
∵DE=EC,
∴∠EDB=∠ECB,
∴∠BED=∠FCE,
在△DBE和△EFC中,
,
∴△DBE≌△EFC,
∴DB=EF=AE;
(3)解:如图3,作EF∥AC交BD于F,
则△BEF为等边三角形,
∴∠EFB=∠EBF=60°,
∴∠EFD=∠EBC=120°,
∵DE=EC,
∴∠EDB=∠ECB,
在△DEF和△CEB中,
,
∴△DEF≌△CEB,
∴DF=BC,
∴DF+FB=AB+BE,
∴BD=AE.
【解析】【解答】解:(1)∵△ABC是等边三角形,E是AB边上中点,
∴AE=BE,∠BCE= ∠BCA=30°,
∵DE=EC,
∴∠EDB=∠ECB=30°,
∵∠ABC=60°,
∴∠BED=30°,
∴∠EDB=∠BED,
∴BD=BE,
∴BD=AE,
故答案为:=;
【分析】(1)根据等边三角形的性质、等腰三角形的三线合一证明;(2)证明△DBE≌△EFC,根据全等三角形的性质证明;(3)作EF∥AC交BD于F,证明△DEF≌△CEB,根据全等三角形的性质证明即可.
1 / 1
