人教版八年级数学上册第十一章三角形单元复习题(含解析)
文档属性
| 名称 | 人教版八年级数学上册第十一章三角形单元复习题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 271.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-18 15:21:15 | ||
图片预览



文档简介
人教版八年级数学上册第十一章三角形单元复习题
一、单选题
1.如图, 是 的外角 的平分线, ,则 的度数是( )
A.64° B.40° C.30° D.32°
2.一个多边形的每一个外角都等于40°,那么这个多边形的内角和为( )
A.1260° B.900° C.1620° D.360°
3.下列各组线段中,能构成三角形的是( )
A.2,5,8 B.3,3,6 C.3,4,5 D.4,5,9
4.若画△ABC中AB边上的高,下列画法中正确的是( )
A. B. C. D.
5.一个多边形的内角和等于 ,则它是( )边形
A.7 B.8 C.9 D.10
6.如图,已知DC‖EG,∠C=40°,∠A=70°,则∠AFE的度数为( )
A.140° B.110° C.90° D.30°
7.内角和与外角和相等的多边形一定是( )
A.八边形 B.六边形 C.五边形 D.四边形
8.如图,锐角△ABC中,AD⊥BC于D,BE⊥AC于E,AD与BE相交于F,那么∠ACB与∠DFE的关系是 ( )
A.互余 B.互补
C.相等 D.不互余、不互补也不相等
9.若 的三边长分别为整数,周长为11,且有一边长为4,则这个三角形的最大边长为( )
A.7 B.6 C.5 D.4
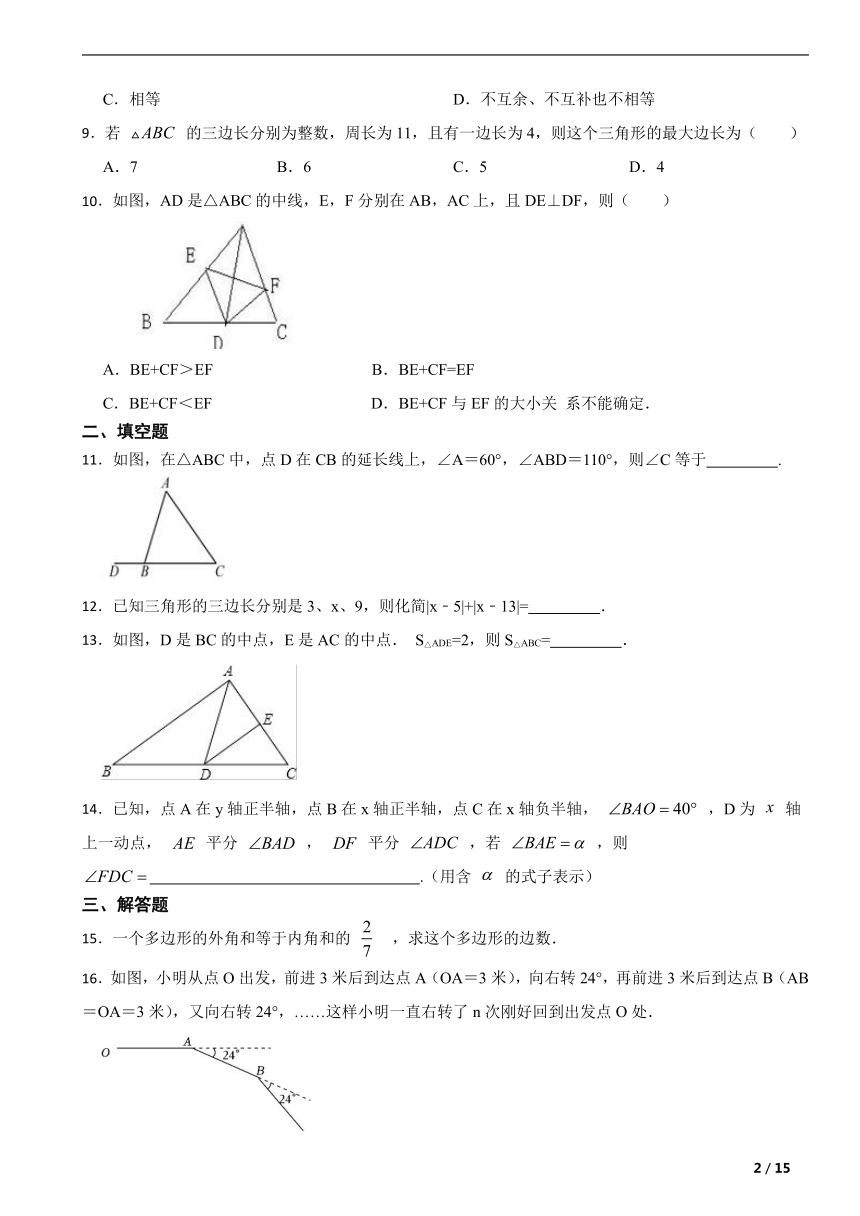
10.如图,AD是△ABC的中线,E,F分别在AB,AC上,且DE⊥DF,则( )
A.BE+CF>EF B.BE+CF=EF
C.BE+CF<EF D.BE+CF与EF的大小关 系不能确定.
二、填空题
11.如图,在△ABC中,点D在CB的延长线上,∠A=60°,∠ABD=110°,则∠C等于 .
12.已知三角形的三边长分别是3、x、9,则化简|x﹣5|+|x﹣13|= .
13.如图,D是BC的中点,E是AC的中点. S△ADE=2,则S△ABC= .
14.已知,点A在y轴正半轴,点B在x轴正半轴,点C在x轴负半轴, ,D为 轴上一动点, 平分 , 平分 ,若 ,则 .(用含 的式子表示)
三、解答题
15.一个多边形的外角和等于内角和的 ,求这个多边形的边数.
16.如图,小明从点O出发,前进3米后到达点A(OA=3米),向右转24°,再前进3米后到达点B(AB=OA=3米),又向右转24°,……这样小明一直右转了n次刚好回到出发点O处.
根据以上信息,解答下列问题:
(1)n的值为 .
(2)小明走出的这n边形的周长为 米.
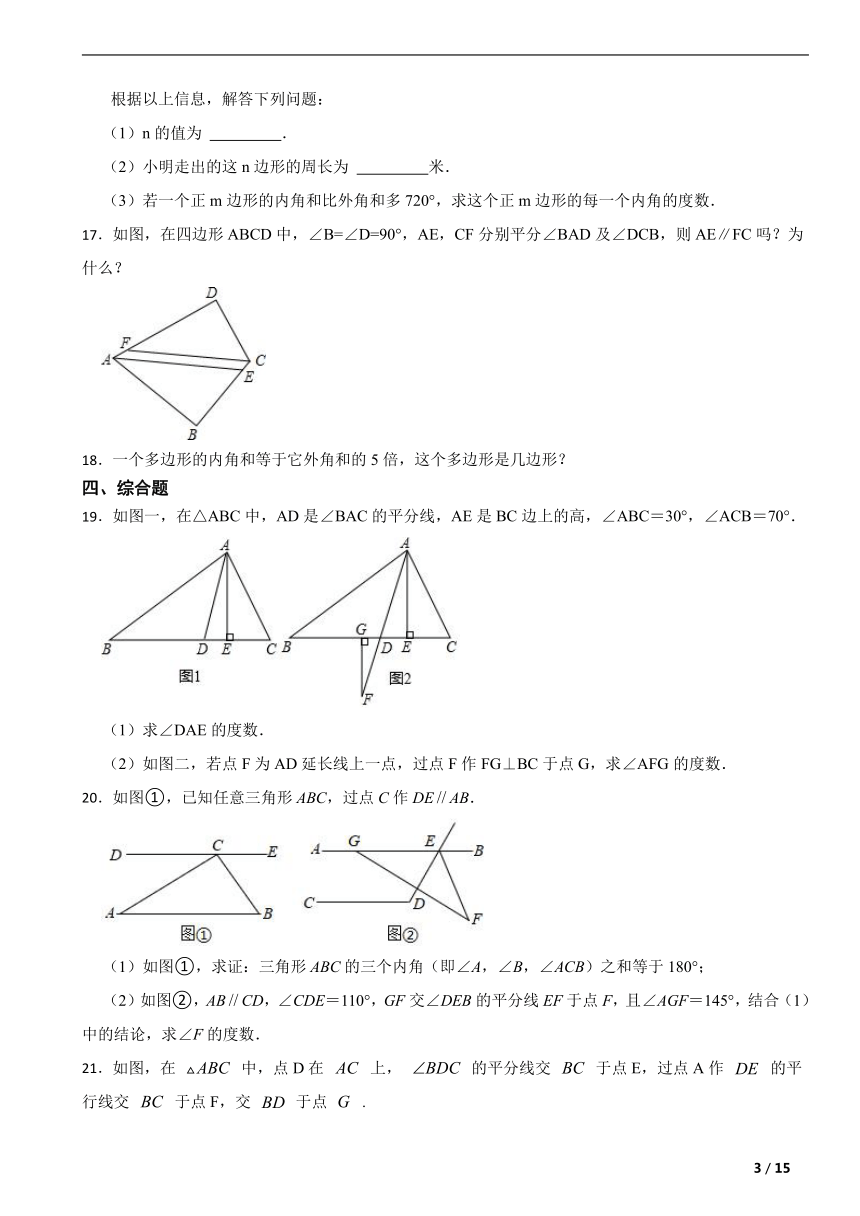
(3)若一个正m边形的内角和比外角和多720°,求这个正m边形的每一个内角的度数.
17.如图,在四边形ABCD中,∠B=∠D=90°,AE,CF分别平分∠BAD及∠DCB,则AE∥FC吗?为什么?
18.一个多边形的内角和等于它外角和的5倍,这个多边形是几边形?
四、综合题
19.如图一,在△ABC中,AD是∠BAC的平分线,AE是BC边上的高,∠ABC=30°,∠ACB=70°.
(1)求∠DAE的度数.
(2)如图二,若点F为AD延长线上一点,过点F作FG⊥BC于点G,求∠AFG的度数.
20.如图①,已知任意三角形ABC,过点C作DEAB.
(1)如图①,求证:三角形ABC的三个内角(即∠A,∠B,∠ACB)之和等于180°;
(2)如图②,ABCD,∠CDE=110°,GF交∠DEB的平分线EF于点F,且∠AGF=145°,结合(1)中的结论,求∠F的度数.
21.如图,在 中,点D在 上, 的平分线交 于点E,过点A作 的平行线交 于点F,交 于点 .
(1)若 , ,求 的度数;
(2)若 ,请说明 .
22.如图
(1)如图1,将长方形纸片ABFE沿着线段DC折叠,CF交AD于点H,过点H作HG∥DC,交线段CB于点G.
①判断∠FHG与∠EDC是否相等,并说明理由;
②说明HG平分∠AHC的理由.
(2)如图2,如果将(1)中的已知条件改为折叠三角形纸片ABE,其它条件不变.HG是否平分∠AHC?如果平分请说明理由;如果不平分,请找出∠CHG,∠AHG与∠E的数量关系并说明理由.
23.已知∠MON
= 50°,OE 平分∠MON,点A、B、C分别是射线OM、OE、ON上的动点(A、B、C不与点O重合),连接AC交射线OE于点D、设∠OAC
= x°.
(1)如图①,若AB//ON,
①则∠ABO 的度数是 ;
②当∠BAD =∠ABD 时,x= ;当∠BAD
= ∠BDA 时,x= .
(2)如图②,若AB⊥OE,则是否存在这样的x值,使得 △ABD 中有一个角是另一个角的两倍.存在,直接写出x的值;不存在,说明理由.
答案解析部分
1.【答案】D
【解析】【解答】解:∵AD∥BC,
∴∠EAD=∠B=32°,
∵AD是△ABC的外角∠EAC的平分线,
∴∠EAC=2∠EAD=64°,
∵∠EAC是△ABC的外角,
∴∠C=∠EAC-∠B=64°-32°=32°,
故答案为:D.
【分析】根据平行线的性质及三角形的外角的性质求出∠C的度数即可。
2.【答案】A
【解析】【解答】360°÷40°=9,
∴(9-2) 180°=1260°.
故答案为:A.
【分析】先利用360°÷40°求出多边形的边数,再根据多边形的内角和公式(n-2) 180°计算即可求解.
3.【答案】C
【解析】【解答】解:A、2+5<8,故A不符合题意。
B、3+3=6,故B不符合题意。
C、3+4>5,故C符合题意。
D、4+5=9,故D不符合题意。
故答案为:C
【分析】由三角形三边关系解题即可。
4.【答案】C
【解析】【解答】过C点作AB边的垂线,交BA的延长线与D,
故答案为:C.
【分析】做哪一条边上的高,即从所对的顶点向这条边和这条边的延长线做垂线即可。
5.【答案】C
【解析】【解答】设这个多边形的边数为 ,
∴ ,
解得: ,
∴这个多边形为九边形.
故答案为: .
【分析】设这个多边形的边数为 ,根据多边形的内角和定理得到 ,然后解方程即可.
6.【答案】B
【解析】【解答】解:∵∠C=40°,∠A=70°,
∴∠ABD=40°+70°=110°,
∵DC∥EG,
∴∠AFE=110°.
故答案为:B.
【分析】先根据三角形外角的性质可求∠ABD,再根据平行线的性质可求∠AFE的度数.
7.【答案】D
【解析】【解答】多边形外角和=360°,
根据题意,得(n﹣2) 180°=360°,解得n=4.
故答案为:D.
【分析】任意多边形的外角和为360°,设多边形的边数为n,然后依据多边形的内角和公式列方程求解即可.
8.【答案】B
【解析】∵AD⊥BC于D,BE⊥AC于E,
∴∠CEF=∠CDF=90°,
∵四边形内角和为360°,
∴∠EFD+∠C=180°,
故选:B.
9.【答案】C
【解析】【解答】解:设这个三角形的最大边长为a,最小边是b.
根据已知,得a+b=7.
根据三角形的三边关系,得:
a-b<4,
由于三角形的三边长都是整数,所以当a-b=3时,解得a=5,b=2,
故答案为:C.
【分析】设这个三角形的最大边长为a,最小边长是b,由已知条件以及三角形三边关系可得:a+b=7,a-b<4,据此求解即可.
10.【答案】A
【解析】【解答】延长ED到G,使DG=ED,连接CG,FG,
在△BED与△CGD中,
∵ ,
∴△BED≌△CGD(SAS),
∴CG=BE,ED=DG,
又∵DE⊥DF
∴FD是EG的垂直平分线,
∴FG=EF
∵GC+CF>FG
∴BE+CF>EF
故答案为:A.
【分析】延长ED到G,使DG=ED,连接CG,FG,易证△BED≌△CGD,利用全等三角形的性质,可证得CG=BE,ED=DG,再证明FD是EG的垂直平分线,就可得出FG=EF,然后根据三角形三边关系定理,可证得结论。
11.【答案】50°
【解析】【解答】解:∵∠ABD=110°,
∴,
∴
故答案为:50°.
【分析】由邻补角定义可求得∠ABC的度数,再根据三角形内角和定理可求得∠C的度数.
12.【答案】8
【解析】【解答】解:∵三角形的三边长分别是3、x、9,
∴6<x<12,
∴x﹣5>0,x﹣13<0,
∴|x﹣5|+|x﹣13|=x﹣5+13﹣x=8,
故答案为:8.
【分析】首先确定第三边的取值范围,从而确定x﹣5和x﹣13的值,然后去绝对值符号求解即可.
13.【答案】8
【解析】【解答】解:∵E是AC的中点,
∴S△ACD=2S△ADE=2×2=4,
∵D是BC的中点,
∴S△ABC=2S△ACD=2×4=8.
故答案为:8.
【分析】根据三角形的中线将三角形分成面积相等的两个三角形先求出△ACD的面积,再求解即可.
14.【答案】 或 或
【解析】【解答】解:当点D在点B的右侧时,如下图,
∵ 平分 ,
∴
∵
∴
∵
∴
∴
∵ 平分
∴ ;
点D在点C的左侧时,画图如下,
∵ 平分 ,
∴
∵
∴
∴
∵ 平分
∴ ;
当点D在点BC之间时,画图如下:
∵ 平分 ,
∴
∵
∴
∴
∵ 平分
∴ ;
故答案为: 或 或 .
【分析】根据题意分:点D在点B的右侧;点D在点C的左侧;点D在点BC之间三种情况分别画图分析,利用角平分线的性质以及三角形的内角和定理求解即可.
15.【答案】解:设这个多边形的边数为n,则
(n-2)·180= 360
解之得 n=9
答:这个多边形的边数是9.
【解析】【分析】 设这个多边形的边数为n ,可得内角和(n-2)·180= 360,外角和为360°,利用“ 这个多边形的外角和等于内角和的 ”列出方程,解之即可.
16.【答案】(1)15
(2)45
(3)解:根据题意,得(m-2)×180°=720°+360°,
解得m=8,
∴这个正m边形的每一个内角的度数为 .
【解析】【解答】解:(1)n=360°÷24°=15;
(2)n边形的周长=15×3=45;
(3)根据题意可得,多边形的内角和为720°+360°=1080°,即(m-2)×180°=1080°,
所以m=8,正八边形的每一个内角为1080°÷8=135°。
【分析】(1)多变形的外角和为360°,根据正多边形的每一个外角为24°,求出n的值;
(2)根据题意可知,正多边形的边长为3,结合n的值,求出周长即可;
(3)根据多边形的内角和定理以及外角和定理求出m的值即可。
17.【答案】解:AE∥FC.
理由如下:∵∠B=∠D=90°,
∴∠BAD+∠BCD=360°-180°=180°,
∵AE,CF分别平分∠BAD及∠DCB,
∴∠DAE= ∠BAD,∠DCF= ∠BCD,
∴∠DAE+∠DCF=90°,
又∵∠D=90°,
∴∠DFC+∠DCF=90°,
∴∠DAE=∠DFC,
∴AE∥FC.
【解析】【分析】根据四边形的内角和定理∠BAD+∠BCD=180°,再根据角平分线的定义求出∠DAE+∠DCF=90°,然后根据直角三角形两锐角互余求出∠DFC+∠DCF=90°,从而得到∠DAE=∠DFC,最后根据同位角相等,两直线平行即可得证.
18.【答案】解:设多边形的边数为n,
由题意得,(n 2) 180 =5×360°,
解得n=12.
故这个多边形的边数是12.
【解析】【分析】根据多边形的内角和公式(n-2) 180°和外角和定理列出方程,然后求解即可.
19.【答案】(1)解:在中,
,,
平分
,
在中,
为三角形的高,
.
在中,.
(2)解:
由(1)可知
.
【解析】【分析】(1)先利用三角形的内角和求出∠BAC的度数,再利用角平分线的定义可得,再利用三角形的内角和求出即可;
(2)利用平行线的性质可得,再根据,可得。
20.【答案】(1)证明:∵DE∥AB,
∴∠A=∠DCE,∠B=∠ECB,
∵∠DCE=180°,
∴∠DCA+∠ACB+∠ECB=180°,
∴∠A+∠ACB+∠B=180°.
(2)解: ∵AB∥CD,
∴∠CDE=∠BED=110°,
∵EF平分∠BED,
∴∠BEF= ∠BED=55°,
∵∠AGF=145°,
∴∠FGE=35°,
∵∠BEF=∠F+∠EGF,
∴∠F=55°﹣35°=20°.
【解析】【分析】(1)利用平行线的性质,根据平角为180°证明三角形内角和定理;(2)根据∠BEF=∠F+∠EGF,想办法求出∠EGF,∠BEF即可解决问题
21.【答案】(1)解:∵AF∥DE,∠2=80°,
∴∠4=∠2=80°,
∵∠4=∠1+∠BDE,∠1=30°,
∴∠BDE=80°-30°=50°,
∵DE是∠BDC的平分线,
∴∠BDC=2∠BDE=100°,
∴∠C=180°-∠1-∠BDC=180°-30°-100°=50°
(2)解:由(1)得:∠4=∠2=∠1+∠5+∠3,即∠1=∠4-∠5-∠3①,
∵∠BDC=2∠ABC,即 ∠BDC=∠BDE=∠ABC=∠1+∠5,
∴∠4=∠1+∠BDE=∠1+∠1+∠5=2∠1+∠5,即∠4=2∠1+∠5②,
①代入②得:∠4=2∠4-2∠5-2∠3+∠5,
整理得:∠4=∠5+2∠3
【解析】【分析】(1)利用平行线的性质可求出∠4的度数,再利用三角形的外角的性质可求出∠BDE的度数;利用角平分线的定义求出∠BDC的度数,然后利用三角形的内角和定理求出∠C的度数.
(2)利用三角形的外角的性质可证得∠1=∠4-∠5-∠3①;再证明∠4=2∠1+∠5②,根据①②可证得结论.
22.【答案】(1)解:①如图1, ∵DE∥CF, ∴∠EDA=∠FHA(两直线平行,同位角相等), ∵HG∥DC, ∠ADC=∠AHG(两直线平行,同位角相等), ∴∠EDA +∠ADC=∠FHA +∠AHG, ∴∠FHG=∠EDC. ② HG平分∠AHC,理由如下: 将图形折回到其原始状态,E的对应点为N,F的对应点为M, 方法1:由折叠知∠NDC=∠EDC, ∵∠FHG=∠EDC. ∴∠FHG=∠NDC. ∵DC∥HG, ∴∠NDC=∠DHG ∴∠DHG=∠FHG. ∵∠DHC=∠FH A(对顶角相等), ∴∠DHG-∠DHC.=∠FHG-∠FH A ∴∠CHG=∠AHG, ∴HG平分∠AHC.
方法2:由折叠知∠FCD=∠DCM.
∵HG∥DC, ∴∠DCM=∠HGC(两直线平行,同位角相等), ∠DCH=∠CHG(两直线平行,内错角相等), ∵AD∥BC, ∴∠CGH=∠AHG(两直线平行,内错角相等), ∴∠CHG=∠AHG, 即HG平分∠AHC.
(2)解:HG不再平分∠AHC.∠AHG=∠CHG+∠E.
理由如下:
如图2,延长线段AD和BC交于点F,
得到∠ECD=∠FCD.
∵HG∥DC,
∴∠CHG=∠DCH=∠FCD,
∠AHG=∠ADC,
∵∠ADC+∠FDC=180 (平角的意义),
又∵∠F+∠FCD+∠FDC=180 (三角形内角和为180 ),
∴∠AHG=∠CHG+∠E
【解析】【分析】(1) ①根据平行线性质得∠EDA=∠FHA,∠ADC=∠AHG,由角的计算即可得证.
② HG平分∠AHC,理由如下:将图形折回到其原始状态,E的对应点为N,F的对应点为M,由折叠性质知:∠FCD=∠DCM,根据平行线性质得:∠DCM=∠HGC,∠DCH=∠CHG,∠CGH=∠AHG,等量代换得∠CHG=∠AHG,根据角平分线定义即可得证.
(2) HG不再平分∠AHC,∠AHG=∠CHG+∠E;理由如下:如图:延长线段AD和BC交于点F,根据平行线性质得:∠CHG=∠DCH=∠FCD,∠AHG=∠ADC,由三角形内角和定理、等量代换即可得证.
23.【答案】(1)25°;105;52.5
(2)解:存在,推导如下
当点D在线段OB上时,如图③所示:
图③
i)当∠ABD=2∠DAB=90°时,则∠ADB=∠DAB=45°,
∵∠AOD+∠OAC=∠ADB,
∴∠OAC=∠ADB-∠AOD=45°-25°=20°,
ii)当∠ADB=2∠DAB时,∵∠ABD=90°,∴∠ADB=60°,
∵∠AOD+∠OAC=∠ADB,
∴∠OAC=∠ADB-∠AOD=60°-25°=35°,
iii) 当∠DAB=2∠ADB时, ∵∠ABD=90°,∴∠ADB=30°,
∵∠AOD+∠OAC=∠ADB,
∴∠OAC=∠ADB-∠AOD=30°-25°=5°.
当点D在线段OB延长线上时,如图③所示:
图③
i)当∠ABD=2∠DAB=90°时,则∠ADB=∠DAB=45°,
∵∠AOD+∠OAC+∠ADB=180°,
∴∠OAC=180°-∠AOD-∠ADB=180°-25°-45°=110°;
ii)当∠ADB=2∠DAB时,∵∠ABD=90°,∴∠ADB=60°,
∵∠AOD+∠OAC+∠ADB=180°,
∴∠OAC=180°-∠AOD-∠ADB=180°-25°-60°=95°;
iii) 当∠DAB=2∠ADB时, ∵∠ABD=90°,∴∠ADB=30°,
∵∠AOD+∠OAC+∠ADB=180°,
∴∠OAC=180°-∠AOD-∠ADB=180°-25°-30°=125°;
综上所述,存在这样的
∠OAC,使得 △ABD 中有一个角是另一个角的两倍,其值x
为20,110,5,125,35,95.
【解析】【解答】解:(1)①∵∠MON=50°,OE平分∠MON∴∠AOB=∠BON=25°
∵AB∥ON∴∠ABO=25°
②当∠BAD=∠ABD,则∠BAD=25°
∵∠AOB+∠ABO+∠OAB=180°
∴∠AOB+∠ABO+∠OAC+∠BAD=180°
∴∠OAC=180°-∠AOB-∠ABO-∠BAD =180°-25°-25°-25°=105°
当∠BAD=∠BDA,∵∠ABO=25°
∴∠BAD=77.5°
∵∠AOB+∠ABO+∠OAB=180°
∴∠OAB=180°-∠ABO-∠AOB=180°-25°-25°=130°
∴∠OAC=∠OAB-∠BAD=130°-77.5°=52.5°
故答案为:①25°; ②105,52.5;
【分析】(1)利用角平分线的性质求出∠ABO的度数是关键,利用三角形的内角和定理及其推论计算求解即可.(2)按点D在线段OB上或OB的延长线上分两大类,再根据△ABD 中有一个角是另一个角的两倍的三种可能性再分类,利用三角形的内角和及其推论分别求解计算即可.
1 / 1
一、单选题
1.如图, 是 的外角 的平分线, ,则 的度数是( )
A.64° B.40° C.30° D.32°
2.一个多边形的每一个外角都等于40°,那么这个多边形的内角和为( )
A.1260° B.900° C.1620° D.360°
3.下列各组线段中,能构成三角形的是( )
A.2,5,8 B.3,3,6 C.3,4,5 D.4,5,9
4.若画△ABC中AB边上的高,下列画法中正确的是( )
A. B. C. D.
5.一个多边形的内角和等于 ,则它是( )边形
A.7 B.8 C.9 D.10
6.如图,已知DC‖EG,∠C=40°,∠A=70°,则∠AFE的度数为( )
A.140° B.110° C.90° D.30°
7.内角和与外角和相等的多边形一定是( )
A.八边形 B.六边形 C.五边形 D.四边形
8.如图,锐角△ABC中,AD⊥BC于D,BE⊥AC于E,AD与BE相交于F,那么∠ACB与∠DFE的关系是 ( )
A.互余 B.互补
C.相等 D.不互余、不互补也不相等
9.若 的三边长分别为整数,周长为11,且有一边长为4,则这个三角形的最大边长为( )
A.7 B.6 C.5 D.4
10.如图,AD是△ABC的中线,E,F分别在AB,AC上,且DE⊥DF,则( )
A.BE+CF>EF B.BE+CF=EF
C.BE+CF<EF D.BE+CF与EF的大小关 系不能确定.
二、填空题
11.如图,在△ABC中,点D在CB的延长线上,∠A=60°,∠ABD=110°,则∠C等于 .
12.已知三角形的三边长分别是3、x、9,则化简|x﹣5|+|x﹣13|= .
13.如图,D是BC的中点,E是AC的中点. S△ADE=2,则S△ABC= .
14.已知,点A在y轴正半轴,点B在x轴正半轴,点C在x轴负半轴, ,D为 轴上一动点, 平分 , 平分 ,若 ,则 .(用含 的式子表示)
三、解答题
15.一个多边形的外角和等于内角和的 ,求这个多边形的边数.
16.如图,小明从点O出发,前进3米后到达点A(OA=3米),向右转24°,再前进3米后到达点B(AB=OA=3米),又向右转24°,……这样小明一直右转了n次刚好回到出发点O处.
根据以上信息,解答下列问题:
(1)n的值为 .
(2)小明走出的这n边形的周长为 米.
(3)若一个正m边形的内角和比外角和多720°,求这个正m边形的每一个内角的度数.
17.如图,在四边形ABCD中,∠B=∠D=90°,AE,CF分别平分∠BAD及∠DCB,则AE∥FC吗?为什么?
18.一个多边形的内角和等于它外角和的5倍,这个多边形是几边形?
四、综合题
19.如图一,在△ABC中,AD是∠BAC的平分线,AE是BC边上的高,∠ABC=30°,∠ACB=70°.
(1)求∠DAE的度数.
(2)如图二,若点F为AD延长线上一点,过点F作FG⊥BC于点G,求∠AFG的度数.
20.如图①,已知任意三角形ABC,过点C作DEAB.
(1)如图①,求证:三角形ABC的三个内角(即∠A,∠B,∠ACB)之和等于180°;
(2)如图②,ABCD,∠CDE=110°,GF交∠DEB的平分线EF于点F,且∠AGF=145°,结合(1)中的结论,求∠F的度数.
21.如图,在 中,点D在 上, 的平分线交 于点E,过点A作 的平行线交 于点F,交 于点 .
(1)若 , ,求 的度数;
(2)若 ,请说明 .
22.如图
(1)如图1,将长方形纸片ABFE沿着线段DC折叠,CF交AD于点H,过点H作HG∥DC,交线段CB于点G.
①判断∠FHG与∠EDC是否相等,并说明理由;
②说明HG平分∠AHC的理由.
(2)如图2,如果将(1)中的已知条件改为折叠三角形纸片ABE,其它条件不变.HG是否平分∠AHC?如果平分请说明理由;如果不平分,请找出∠CHG,∠AHG与∠E的数量关系并说明理由.
23.已知∠MON
= 50°,OE 平分∠MON,点A、B、C分别是射线OM、OE、ON上的动点(A、B、C不与点O重合),连接AC交射线OE于点D、设∠OAC
= x°.
(1)如图①,若AB//ON,
①则∠ABO 的度数是 ;
②当∠BAD =∠ABD 时,x= ;当∠BAD
= ∠BDA 时,x= .
(2)如图②,若AB⊥OE,则是否存在这样的x值,使得 △ABD 中有一个角是另一个角的两倍.存在,直接写出x的值;不存在,说明理由.
答案解析部分
1.【答案】D
【解析】【解答】解:∵AD∥BC,
∴∠EAD=∠B=32°,
∵AD是△ABC的外角∠EAC的平分线,
∴∠EAC=2∠EAD=64°,
∵∠EAC是△ABC的外角,
∴∠C=∠EAC-∠B=64°-32°=32°,
故答案为:D.
【分析】根据平行线的性质及三角形的外角的性质求出∠C的度数即可。
2.【答案】A
【解析】【解答】360°÷40°=9,
∴(9-2) 180°=1260°.
故答案为:A.
【分析】先利用360°÷40°求出多边形的边数,再根据多边形的内角和公式(n-2) 180°计算即可求解.
3.【答案】C
【解析】【解答】解:A、2+5<8,故A不符合题意。
B、3+3=6,故B不符合题意。
C、3+4>5,故C符合题意。
D、4+5=9,故D不符合题意。
故答案为:C
【分析】由三角形三边关系解题即可。
4.【答案】C
【解析】【解答】过C点作AB边的垂线,交BA的延长线与D,
故答案为:C.
【分析】做哪一条边上的高,即从所对的顶点向这条边和这条边的延长线做垂线即可。
5.【答案】C
【解析】【解答】设这个多边形的边数为 ,
∴ ,
解得: ,
∴这个多边形为九边形.
故答案为: .
【分析】设这个多边形的边数为 ,根据多边形的内角和定理得到 ,然后解方程即可.
6.【答案】B
【解析】【解答】解:∵∠C=40°,∠A=70°,
∴∠ABD=40°+70°=110°,
∵DC∥EG,
∴∠AFE=110°.
故答案为:B.
【分析】先根据三角形外角的性质可求∠ABD,再根据平行线的性质可求∠AFE的度数.
7.【答案】D
【解析】【解答】多边形外角和=360°,
根据题意,得(n﹣2) 180°=360°,解得n=4.
故答案为:D.
【分析】任意多边形的外角和为360°,设多边形的边数为n,然后依据多边形的内角和公式列方程求解即可.
8.【答案】B
【解析】∵AD⊥BC于D,BE⊥AC于E,
∴∠CEF=∠CDF=90°,
∵四边形内角和为360°,
∴∠EFD+∠C=180°,
故选:B.
9.【答案】C
【解析】【解答】解:设这个三角形的最大边长为a,最小边是b.
根据已知,得a+b=7.
根据三角形的三边关系,得:
a-b<4,
由于三角形的三边长都是整数,所以当a-b=3时,解得a=5,b=2,
故答案为:C.
【分析】设这个三角形的最大边长为a,最小边长是b,由已知条件以及三角形三边关系可得:a+b=7,a-b<4,据此求解即可.
10.【答案】A
【解析】【解答】延长ED到G,使DG=ED,连接CG,FG,
在△BED与△CGD中,
∵ ,
∴△BED≌△CGD(SAS),
∴CG=BE,ED=DG,
又∵DE⊥DF
∴FD是EG的垂直平分线,
∴FG=EF
∵GC+CF>FG
∴BE+CF>EF
故答案为:A.
【分析】延长ED到G,使DG=ED,连接CG,FG,易证△BED≌△CGD,利用全等三角形的性质,可证得CG=BE,ED=DG,再证明FD是EG的垂直平分线,就可得出FG=EF,然后根据三角形三边关系定理,可证得结论。
11.【答案】50°
【解析】【解答】解:∵∠ABD=110°,
∴,
∴
故答案为:50°.
【分析】由邻补角定义可求得∠ABC的度数,再根据三角形内角和定理可求得∠C的度数.
12.【答案】8
【解析】【解答】解:∵三角形的三边长分别是3、x、9,
∴6<x<12,
∴x﹣5>0,x﹣13<0,
∴|x﹣5|+|x﹣13|=x﹣5+13﹣x=8,
故答案为:8.
【分析】首先确定第三边的取值范围,从而确定x﹣5和x﹣13的值,然后去绝对值符号求解即可.
13.【答案】8
【解析】【解答】解:∵E是AC的中点,
∴S△ACD=2S△ADE=2×2=4,
∵D是BC的中点,
∴S△ABC=2S△ACD=2×4=8.
故答案为:8.
【分析】根据三角形的中线将三角形分成面积相等的两个三角形先求出△ACD的面积,再求解即可.
14.【答案】 或 或
【解析】【解答】解:当点D在点B的右侧时,如下图,
∵ 平分 ,
∴
∵
∴
∵
∴
∴
∵ 平分
∴ ;
点D在点C的左侧时,画图如下,
∵ 平分 ,
∴
∵
∴
∴
∵ 平分
∴ ;
当点D在点BC之间时,画图如下:
∵ 平分 ,
∴
∵
∴
∴
∵ 平分
∴ ;
故答案为: 或 或 .
【分析】根据题意分:点D在点B的右侧;点D在点C的左侧;点D在点BC之间三种情况分别画图分析,利用角平分线的性质以及三角形的内角和定理求解即可.
15.【答案】解:设这个多边形的边数为n,则
(n-2)·180= 360
解之得 n=9
答:这个多边形的边数是9.
【解析】【分析】 设这个多边形的边数为n ,可得内角和(n-2)·180= 360,外角和为360°,利用“ 这个多边形的外角和等于内角和的 ”列出方程,解之即可.
16.【答案】(1)15
(2)45
(3)解:根据题意,得(m-2)×180°=720°+360°,
解得m=8,
∴这个正m边形的每一个内角的度数为 .
【解析】【解答】解:(1)n=360°÷24°=15;
(2)n边形的周长=15×3=45;
(3)根据题意可得,多边形的内角和为720°+360°=1080°,即(m-2)×180°=1080°,
所以m=8,正八边形的每一个内角为1080°÷8=135°。
【分析】(1)多变形的外角和为360°,根据正多边形的每一个外角为24°,求出n的值;
(2)根据题意可知,正多边形的边长为3,结合n的值,求出周长即可;
(3)根据多边形的内角和定理以及外角和定理求出m的值即可。
17.【答案】解:AE∥FC.
理由如下:∵∠B=∠D=90°,
∴∠BAD+∠BCD=360°-180°=180°,
∵AE,CF分别平分∠BAD及∠DCB,
∴∠DAE= ∠BAD,∠DCF= ∠BCD,
∴∠DAE+∠DCF=90°,
又∵∠D=90°,
∴∠DFC+∠DCF=90°,
∴∠DAE=∠DFC,
∴AE∥FC.
【解析】【分析】根据四边形的内角和定理∠BAD+∠BCD=180°,再根据角平分线的定义求出∠DAE+∠DCF=90°,然后根据直角三角形两锐角互余求出∠DFC+∠DCF=90°,从而得到∠DAE=∠DFC,最后根据同位角相等,两直线平行即可得证.
18.【答案】解:设多边形的边数为n,
由题意得,(n 2) 180 =5×360°,
解得n=12.
故这个多边形的边数是12.
【解析】【分析】根据多边形的内角和公式(n-2) 180°和外角和定理列出方程,然后求解即可.
19.【答案】(1)解:在中,
,,
平分
,
在中,
为三角形的高,
.
在中,.
(2)解:
由(1)可知
.
【解析】【分析】(1)先利用三角形的内角和求出∠BAC的度数,再利用角平分线的定义可得,再利用三角形的内角和求出即可;
(2)利用平行线的性质可得,再根据,可得。
20.【答案】(1)证明:∵DE∥AB,
∴∠A=∠DCE,∠B=∠ECB,
∵∠DCE=180°,
∴∠DCA+∠ACB+∠ECB=180°,
∴∠A+∠ACB+∠B=180°.
(2)解: ∵AB∥CD,
∴∠CDE=∠BED=110°,
∵EF平分∠BED,
∴∠BEF= ∠BED=55°,
∵∠AGF=145°,
∴∠FGE=35°,
∵∠BEF=∠F+∠EGF,
∴∠F=55°﹣35°=20°.
【解析】【分析】(1)利用平行线的性质,根据平角为180°证明三角形内角和定理;(2)根据∠BEF=∠F+∠EGF,想办法求出∠EGF,∠BEF即可解决问题
21.【答案】(1)解:∵AF∥DE,∠2=80°,
∴∠4=∠2=80°,
∵∠4=∠1+∠BDE,∠1=30°,
∴∠BDE=80°-30°=50°,
∵DE是∠BDC的平分线,
∴∠BDC=2∠BDE=100°,
∴∠C=180°-∠1-∠BDC=180°-30°-100°=50°
(2)解:由(1)得:∠4=∠2=∠1+∠5+∠3,即∠1=∠4-∠5-∠3①,
∵∠BDC=2∠ABC,即 ∠BDC=∠BDE=∠ABC=∠1+∠5,
∴∠4=∠1+∠BDE=∠1+∠1+∠5=2∠1+∠5,即∠4=2∠1+∠5②,
①代入②得:∠4=2∠4-2∠5-2∠3+∠5,
整理得:∠4=∠5+2∠3
【解析】【分析】(1)利用平行线的性质可求出∠4的度数,再利用三角形的外角的性质可求出∠BDE的度数;利用角平分线的定义求出∠BDC的度数,然后利用三角形的内角和定理求出∠C的度数.
(2)利用三角形的外角的性质可证得∠1=∠4-∠5-∠3①;再证明∠4=2∠1+∠5②,根据①②可证得结论.
22.【答案】(1)解:①如图1, ∵DE∥CF, ∴∠EDA=∠FHA(两直线平行,同位角相等), ∵HG∥DC, ∠ADC=∠AHG(两直线平行,同位角相等), ∴∠EDA +∠ADC=∠FHA +∠AHG, ∴∠FHG=∠EDC. ② HG平分∠AHC,理由如下: 将图形折回到其原始状态,E的对应点为N,F的对应点为M, 方法1:由折叠知∠NDC=∠EDC, ∵∠FHG=∠EDC. ∴∠FHG=∠NDC. ∵DC∥HG, ∴∠NDC=∠DHG ∴∠DHG=∠FHG. ∵∠DHC=∠FH A(对顶角相等), ∴∠DHG-∠DHC.=∠FHG-∠FH A ∴∠CHG=∠AHG, ∴HG平分∠AHC.
方法2:由折叠知∠FCD=∠DCM.
∵HG∥DC, ∴∠DCM=∠HGC(两直线平行,同位角相等), ∠DCH=∠CHG(两直线平行,内错角相等), ∵AD∥BC, ∴∠CGH=∠AHG(两直线平行,内错角相等), ∴∠CHG=∠AHG, 即HG平分∠AHC.
(2)解:HG不再平分∠AHC.∠AHG=∠CHG+∠E.
理由如下:
如图2,延长线段AD和BC交于点F,
得到∠ECD=∠FCD.
∵HG∥DC,
∴∠CHG=∠DCH=∠FCD,
∠AHG=∠ADC,
∵∠ADC+∠FDC=180 (平角的意义),
又∵∠F+∠FCD+∠FDC=180 (三角形内角和为180 ),
∴∠AHG=∠CHG+∠E
【解析】【分析】(1) ①根据平行线性质得∠EDA=∠FHA,∠ADC=∠AHG,由角的计算即可得证.
② HG平分∠AHC,理由如下:将图形折回到其原始状态,E的对应点为N,F的对应点为M,由折叠性质知:∠FCD=∠DCM,根据平行线性质得:∠DCM=∠HGC,∠DCH=∠CHG,∠CGH=∠AHG,等量代换得∠CHG=∠AHG,根据角平分线定义即可得证.
(2) HG不再平分∠AHC,∠AHG=∠CHG+∠E;理由如下:如图:延长线段AD和BC交于点F,根据平行线性质得:∠CHG=∠DCH=∠FCD,∠AHG=∠ADC,由三角形内角和定理、等量代换即可得证.
23.【答案】(1)25°;105;52.5
(2)解:存在,推导如下
当点D在线段OB上时,如图③所示:
图③
i)当∠ABD=2∠DAB=90°时,则∠ADB=∠DAB=45°,
∵∠AOD+∠OAC=∠ADB,
∴∠OAC=∠ADB-∠AOD=45°-25°=20°,
ii)当∠ADB=2∠DAB时,∵∠ABD=90°,∴∠ADB=60°,
∵∠AOD+∠OAC=∠ADB,
∴∠OAC=∠ADB-∠AOD=60°-25°=35°,
iii) 当∠DAB=2∠ADB时, ∵∠ABD=90°,∴∠ADB=30°,
∵∠AOD+∠OAC=∠ADB,
∴∠OAC=∠ADB-∠AOD=30°-25°=5°.
当点D在线段OB延长线上时,如图③所示:
图③
i)当∠ABD=2∠DAB=90°时,则∠ADB=∠DAB=45°,
∵∠AOD+∠OAC+∠ADB=180°,
∴∠OAC=180°-∠AOD-∠ADB=180°-25°-45°=110°;
ii)当∠ADB=2∠DAB时,∵∠ABD=90°,∴∠ADB=60°,
∵∠AOD+∠OAC+∠ADB=180°,
∴∠OAC=180°-∠AOD-∠ADB=180°-25°-60°=95°;
iii) 当∠DAB=2∠ADB时, ∵∠ABD=90°,∴∠ADB=30°,
∵∠AOD+∠OAC+∠ADB=180°,
∴∠OAC=180°-∠AOD-∠ADB=180°-25°-30°=125°;
综上所述,存在这样的
∠OAC,使得 △ABD 中有一个角是另一个角的两倍,其值x
为20,110,5,125,35,95.
【解析】【解答】解:(1)①∵∠MON=50°,OE平分∠MON∴∠AOB=∠BON=25°
∵AB∥ON∴∠ABO=25°
②当∠BAD=∠ABD,则∠BAD=25°
∵∠AOB+∠ABO+∠OAB=180°
∴∠AOB+∠ABO+∠OAC+∠BAD=180°
∴∠OAC=180°-∠AOB-∠ABO-∠BAD =180°-25°-25°-25°=105°
当∠BAD=∠BDA,∵∠ABO=25°
∴∠BAD=77.5°
∵∠AOB+∠ABO+∠OAB=180°
∴∠OAB=180°-∠ABO-∠AOB=180°-25°-25°=130°
∴∠OAC=∠OAB-∠BAD=130°-77.5°=52.5°
故答案为:①25°; ②105,52.5;
【分析】(1)利用角平分线的性质求出∠ABO的度数是关键,利用三角形的内角和定理及其推论计算求解即可.(2)按点D在线段OB上或OB的延长线上分两大类,再根据△ABD 中有一个角是另一个角的两倍的三种可能性再分类,利用三角形的内角和及其推论分别求解计算即可.
1 / 1
