2023-2024学年人教版九年级数学下册复习卷(含答案)
文档属性
| 名称 | 2023-2024学年人教版九年级数学下册复习卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 863.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-18 15:19:24 | ||
图片预览

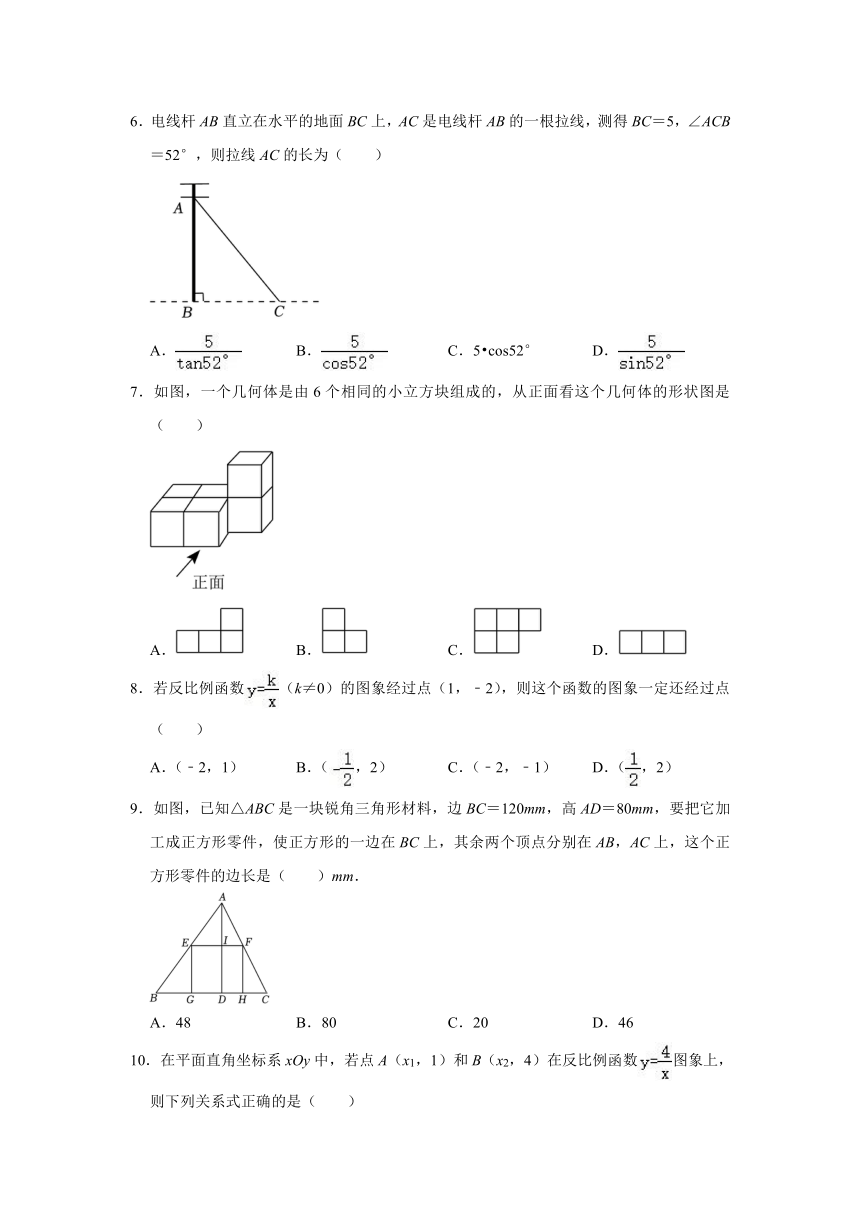

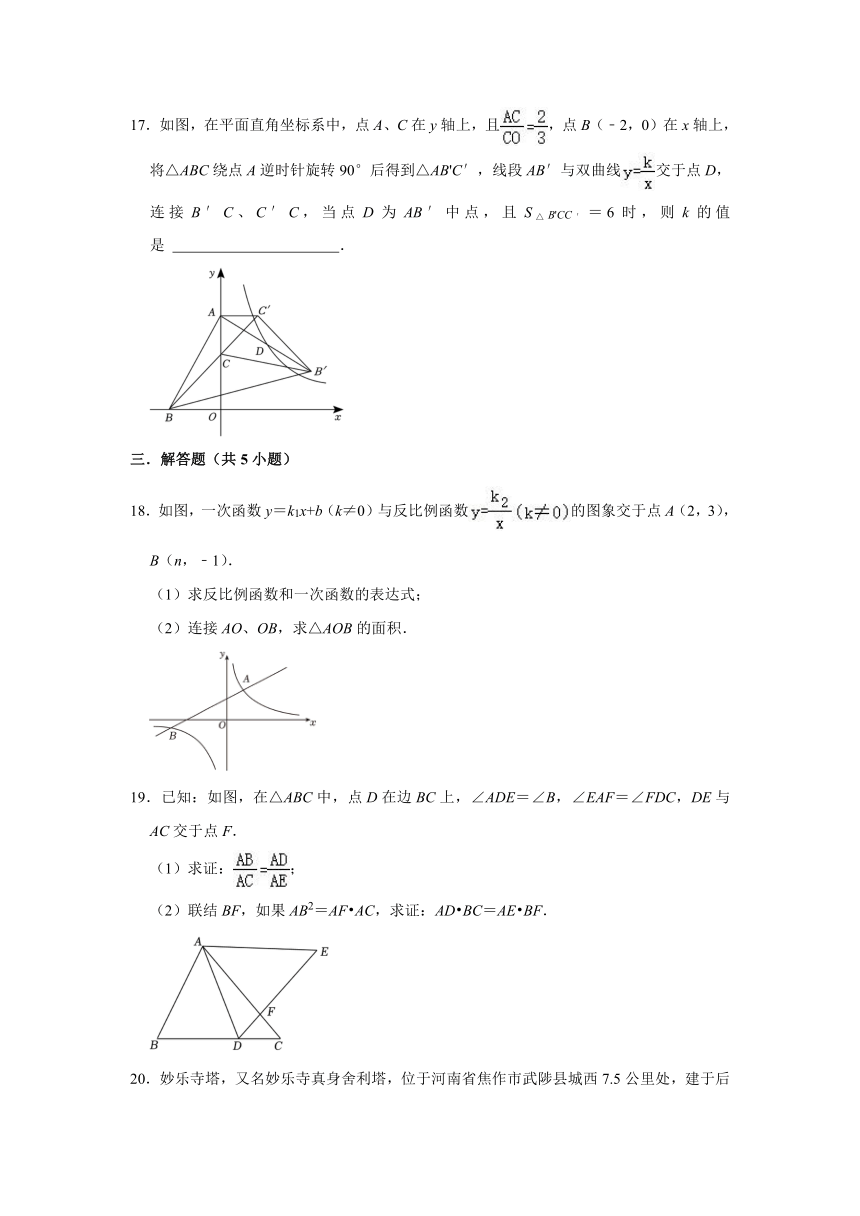

文档简介
2023-2024学年人教版九年级数学下册复习卷
一.选择题(共12小题)
1.tan30°的值等于( )
A. B. C. D.
2.如图所示的几何体的左视图是( )
A. B.
C. D.
3.已知近视眼镜的度数D(度)与镜片焦距f(米)成反比例函数关系,其图象如图所示,小慧想通过矫正治疗使近视眼镜的度数D不超过200度,则她需佩戴镜片的焦距f应满足( )
A.f<0.5 B.f>0.5 C.f≤0.5 D.f≥0.5
4.如图,在矩形ABCD中,AB=6,BC=9,点E、F分别在边AB、BC上,AE=2,BD、EF交于点G,若G是EF的中点,则BF的长是( )
A.5 B.6 C.6.4 D.7.2
5.下列选项中的两个图形一定相似的是( )
A.两个平行四边形 B.两个圆
C.两个菱形 D.两个等腰三角形
6.电线杆AB直立在水平的地面BC上,AC是电线杆AB的一根拉线,测得BC=5,∠ACB=52°,则拉线AC的长为( )
A. B. C.5 cos52° D.
7.如图,一个几何体是由6个相同的小立方块组成的,从正面看这个几何体的形状图是( )
A. B. C. D.
8.若反比例函数(k≠0)的图象经过点(1,﹣2),则这个函数的图象一定还经过点( )
A.(﹣2,1) B.(,2) C.(﹣2,﹣1) D.(,2)
9.如图,已知△ABC是一块锐角三角形材料,边BC=120mm,高AD=80mm,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上,这个正方形零件的边长是( )mm.
A.48 B.80 C.20 D.46
10.在平面直角坐标系xOy中,若点A(x1,1)和B(x2,4)在反比例函数图象上,则下列关系式正确的是( )
A.0<x2<x1 B.0<x1<x2 C.x1<x2<0 D.x2<x1<0
11.若α是锐角,tanα=1,则cosα的值是( )
A. B. C. D.1
12.已知△ABC中,BC=a,AC=b,AB=c,且2b=a+c,延长CA到D,使AD=AB,连接BD,则tan∠BCA的值为( )
A. B. C. D.
二.填空题(共5小题)
13.已知△ABC与△A′B′C′的相似比为,且S△ABC+S△A′B′C′=91,则△A′B′C′的面积是 .
14.如图,从三个不同方向看同一个几何体得到如下平面图形,则这个几何体的侧面积是 cm2.
15.如图,直线AB过原点O,与反比例函数交于A,B两点,AC∥y轴,BC∥x轴,若△ABC的面积为2,则k的值为 .
16.如图,为了测得某建筑物的高度AB,在C处用高为1m的测角仪CF,测得该建筑物顶端A的仰角为45°,再向建筑物方向前进40m,又测得该建筑物顶端A的仰角为60°,则该建筑物的高度AB为 (结果保留根号).
17.如图,在平面直角坐标系中,点A、C在y轴上,且,点B(﹣2,0)在x轴上,将△ABC绕点A逆时针旋转90°后得到△AB'C′,线段AB′与双曲线交于点D,连接B′C、C′C,当点D为AB′中点,且S△B'CC′=6时,则k的值是 .
三.解答题(共5小题)
18.如图,一次函数y=k1x+b(k≠0)与反比例函数的图象交于点A(2,3),B(n,﹣1).
(1)求反比例函数和一次函数的表达式;
(2)连接AO、OB,求△AOB的面积.
19.已知:如图,在△ABC中,点D在边BC上,∠ADE=∠B,∠EAF=∠FDC,DE与AC交于点F.
(1)求证:;
(2)联结BF,如果AB2=AF AC,求证:AD BC=AE BF.
20.妙乐寺塔,又名妙乐寺真身舍利塔,位于河南省焦作市武陟县城西7.5公里处,建于后周显德二年,是我国现存最古老、规模最大、保存最为完整的五代大型砖塔,2001年6月25日妙乐寺塔作为五代时期古建筑,被国务院公布为第五批全国重点文物保护单位.某数学兴趣小组准备测量妙乐寺塔的高度,由于塔底不可到达,小组准备用无人机测量,组员小明操作无人机飞至离地面高度为60米的C处时,测得妙乐寺塔AB的顶端A的俯角为45°,他操控无人机水平飞行70米至塔另一侧D处时,测得塔AB的顶端A的俯角为25°.已知A,B,C,D在同一平面内,求妙乐寺塔AB的高度.(精确到0.1米,参考数据:sin25°≈0.42,cos25°≈0.90,tan25°≈0.47,≈1.41)
21.如图,直线y=﹣x﹣1与双曲线交于A、B两点.
(1)求A、B两点的坐标.
(2)根据图象写出一次函数的值大于反比例函数的值的x的取值范围.
(3)连接OA、OB,求△AOB的面积.
22.如图,平台AB上有一棵直立的大树CD,平台的边缘B处有一棵直立的小树BE,平台边缘B外有一个向下的斜坡BG.小明想利用数学课上学习的知识测量大树CD的高度.一天,他发现大树的影子一部分落在平台CB上,一部分落在斜坡上,而且大树的顶端D与小树顶端E的影子恰好重合,且都落在斜坡上的F处,经测量,CB长5米,BF长2米,小树BE高1.8米,斜坡BG与平台AB所成的∠ABG=150°.请你帮小明求出大树CD的高度(结果保留一位小数).
参考答案
一.选择题(共12小题)
1--10CDDBB BAAAA 11--12BB
二.填空题(共5小题)
13.63
14.72
15.1
16..
17..
三.解答题(共5小题)
18.解:(1)将A(2,3)代入y=得3=k2,
解得k2=6,
∴y=,
把B(n,﹣1)代入y=得﹣1=,
解得n=﹣6,
∴点B坐标为(﹣6,﹣1).
把A(2,3),B(﹣6,﹣1)代入y=k1x+b得:
,解得:,
∴y=x+2.
(2)设直线与x轴的交点为C,令x+2=t=0,
∴C(﹣4,0),
∴S△AOB=S△AOC+S△COB==6+2=8.
19.(1)证明:∵∠EAF+∠AFE+∠E=∠FDC+∠CFD+∠C=180°,∠EAF=∠FDC,∠AFE=∠CFD,
∴∠E=∠C,
∵∠ADE=∠B,
∴△ADE∽△ABC,
∴=;
(2)证明:如图,∵AB2=AF AC,
∴=,
∵∠BAC=∠FAB,
∴△ABC∽△AFB,
∴=,
由(1)知:=,
∴=,
∴AD BC=AE BF.
20.解:过点A作AE⊥CD,垂足为E,设AE=x米.
在Rt△ACE中,
∵∠C=45°,
∴CE=AE=x米.
在Rt△ADE中,
∵∠D=25°,tanD=,
∴DE==≈.
∵DE+CE=CD,
∴+x=70.
∴x≈22.38米.
∴AB=BE﹣AE
=60﹣22.38
=37.62
≈37.6(米).
答:妙乐寺塔AB的高度约为37.6米.
21.解:(1)由得 ,
故A(﹣2,1),B(1,﹣2);
(2)由函数图象可知,x<﹣2或0<x<1时,一次函数的值大于反比例函数的值;
(3)设直线y=﹣x﹣1与y轴交于C,则C(0,﹣1)
S△OAB=S△OAC+S△OBC==.
22.解:延长CB交EF于点H,过点F作FM⊥EB的延长线于点M
∵∠ABG=150°,BE⊥CB
∴∠MBF=150°﹣90°=60°
∴∠MFB=30°
∵BF的长为2米,
∴BM=1米,MF=米
∵BE⊥CB,MF⊥BE
∴BH∥MF
∴△EBH∽△EMF
∴=
又∵EB=1.8米
∴=
∴BH=
∵BE∥CD
∴△HBE∽△HCD
∴=
∵CB=5
∴=
∴CD=15.8米
∴大树CD的高度为15.8米
一.选择题(共12小题)
1.tan30°的值等于( )
A. B. C. D.
2.如图所示的几何体的左视图是( )
A. B.
C. D.
3.已知近视眼镜的度数D(度)与镜片焦距f(米)成反比例函数关系,其图象如图所示,小慧想通过矫正治疗使近视眼镜的度数D不超过200度,则她需佩戴镜片的焦距f应满足( )
A.f<0.5 B.f>0.5 C.f≤0.5 D.f≥0.5
4.如图,在矩形ABCD中,AB=6,BC=9,点E、F分别在边AB、BC上,AE=2,BD、EF交于点G,若G是EF的中点,则BF的长是( )
A.5 B.6 C.6.4 D.7.2
5.下列选项中的两个图形一定相似的是( )
A.两个平行四边形 B.两个圆
C.两个菱形 D.两个等腰三角形
6.电线杆AB直立在水平的地面BC上,AC是电线杆AB的一根拉线,测得BC=5,∠ACB=52°,则拉线AC的长为( )
A. B. C.5 cos52° D.
7.如图,一个几何体是由6个相同的小立方块组成的,从正面看这个几何体的形状图是( )
A. B. C. D.
8.若反比例函数(k≠0)的图象经过点(1,﹣2),则这个函数的图象一定还经过点( )
A.(﹣2,1) B.(,2) C.(﹣2,﹣1) D.(,2)
9.如图,已知△ABC是一块锐角三角形材料,边BC=120mm,高AD=80mm,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上,这个正方形零件的边长是( )mm.
A.48 B.80 C.20 D.46
10.在平面直角坐标系xOy中,若点A(x1,1)和B(x2,4)在反比例函数图象上,则下列关系式正确的是( )
A.0<x2<x1 B.0<x1<x2 C.x1<x2<0 D.x2<x1<0
11.若α是锐角,tanα=1,则cosα的值是( )
A. B. C. D.1
12.已知△ABC中,BC=a,AC=b,AB=c,且2b=a+c,延长CA到D,使AD=AB,连接BD,则tan∠BCA的值为( )
A. B. C. D.
二.填空题(共5小题)
13.已知△ABC与△A′B′C′的相似比为,且S△ABC+S△A′B′C′=91,则△A′B′C′的面积是 .
14.如图,从三个不同方向看同一个几何体得到如下平面图形,则这个几何体的侧面积是 cm2.
15.如图,直线AB过原点O,与反比例函数交于A,B两点,AC∥y轴,BC∥x轴,若△ABC的面积为2,则k的值为 .
16.如图,为了测得某建筑物的高度AB,在C处用高为1m的测角仪CF,测得该建筑物顶端A的仰角为45°,再向建筑物方向前进40m,又测得该建筑物顶端A的仰角为60°,则该建筑物的高度AB为 (结果保留根号).
17.如图,在平面直角坐标系中,点A、C在y轴上,且,点B(﹣2,0)在x轴上,将△ABC绕点A逆时针旋转90°后得到△AB'C′,线段AB′与双曲线交于点D,连接B′C、C′C,当点D为AB′中点,且S△B'CC′=6时,则k的值是 .
三.解答题(共5小题)
18.如图,一次函数y=k1x+b(k≠0)与反比例函数的图象交于点A(2,3),B(n,﹣1).
(1)求反比例函数和一次函数的表达式;
(2)连接AO、OB,求△AOB的面积.
19.已知:如图,在△ABC中,点D在边BC上,∠ADE=∠B,∠EAF=∠FDC,DE与AC交于点F.
(1)求证:;
(2)联结BF,如果AB2=AF AC,求证:AD BC=AE BF.
20.妙乐寺塔,又名妙乐寺真身舍利塔,位于河南省焦作市武陟县城西7.5公里处,建于后周显德二年,是我国现存最古老、规模最大、保存最为完整的五代大型砖塔,2001年6月25日妙乐寺塔作为五代时期古建筑,被国务院公布为第五批全国重点文物保护单位.某数学兴趣小组准备测量妙乐寺塔的高度,由于塔底不可到达,小组准备用无人机测量,组员小明操作无人机飞至离地面高度为60米的C处时,测得妙乐寺塔AB的顶端A的俯角为45°,他操控无人机水平飞行70米至塔另一侧D处时,测得塔AB的顶端A的俯角为25°.已知A,B,C,D在同一平面内,求妙乐寺塔AB的高度.(精确到0.1米,参考数据:sin25°≈0.42,cos25°≈0.90,tan25°≈0.47,≈1.41)
21.如图,直线y=﹣x﹣1与双曲线交于A、B两点.
(1)求A、B两点的坐标.
(2)根据图象写出一次函数的值大于反比例函数的值的x的取值范围.
(3)连接OA、OB,求△AOB的面积.
22.如图,平台AB上有一棵直立的大树CD,平台的边缘B处有一棵直立的小树BE,平台边缘B外有一个向下的斜坡BG.小明想利用数学课上学习的知识测量大树CD的高度.一天,他发现大树的影子一部分落在平台CB上,一部分落在斜坡上,而且大树的顶端D与小树顶端E的影子恰好重合,且都落在斜坡上的F处,经测量,CB长5米,BF长2米,小树BE高1.8米,斜坡BG与平台AB所成的∠ABG=150°.请你帮小明求出大树CD的高度(结果保留一位小数).
参考答案
一.选择题(共12小题)
1--10CDDBB BAAAA 11--12BB
二.填空题(共5小题)
13.63
14.72
15.1
16..
17..
三.解答题(共5小题)
18.解:(1)将A(2,3)代入y=得3=k2,
解得k2=6,
∴y=,
把B(n,﹣1)代入y=得﹣1=,
解得n=﹣6,
∴点B坐标为(﹣6,﹣1).
把A(2,3),B(﹣6,﹣1)代入y=k1x+b得:
,解得:,
∴y=x+2.
(2)设直线与x轴的交点为C,令x+2=t=0,
∴C(﹣4,0),
∴S△AOB=S△AOC+S△COB==6+2=8.
19.(1)证明:∵∠EAF+∠AFE+∠E=∠FDC+∠CFD+∠C=180°,∠EAF=∠FDC,∠AFE=∠CFD,
∴∠E=∠C,
∵∠ADE=∠B,
∴△ADE∽△ABC,
∴=;
(2)证明:如图,∵AB2=AF AC,
∴=,
∵∠BAC=∠FAB,
∴△ABC∽△AFB,
∴=,
由(1)知:=,
∴=,
∴AD BC=AE BF.
20.解:过点A作AE⊥CD,垂足为E,设AE=x米.
在Rt△ACE中,
∵∠C=45°,
∴CE=AE=x米.
在Rt△ADE中,
∵∠D=25°,tanD=,
∴DE==≈.
∵DE+CE=CD,
∴+x=70.
∴x≈22.38米.
∴AB=BE﹣AE
=60﹣22.38
=37.62
≈37.6(米).
答:妙乐寺塔AB的高度约为37.6米.
21.解:(1)由得 ,
故A(﹣2,1),B(1,﹣2);
(2)由函数图象可知,x<﹣2或0<x<1时,一次函数的值大于反比例函数的值;
(3)设直线y=﹣x﹣1与y轴交于C,则C(0,﹣1)
S△OAB=S△OAC+S△OBC==.
22.解:延长CB交EF于点H,过点F作FM⊥EB的延长线于点M
∵∠ABG=150°,BE⊥CB
∴∠MBF=150°﹣90°=60°
∴∠MFB=30°
∵BF的长为2米,
∴BM=1米,MF=米
∵BE⊥CB,MF⊥BE
∴BH∥MF
∴△EBH∽△EMF
∴=
又∵EB=1.8米
∴=
∴BH=
∵BE∥CD
∴△HBE∽△HCD
∴=
∵CB=5
∴=
∴CD=15.8米
∴大树CD的高度为15.8米
同课章节目录
