人教版七年级数学上册第四章几何图形初步单元复习题(含解析)
文档属性
| 名称 | 人教版七年级数学上册第四章几何图形初步单元复习题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 407.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-18 00:00:00 | ||
图片预览



文档简介
人教版七年级数学上册第四章几何图形初步单元复习题
一、单选题
1.如图,甲从A处出发沿北偏东60°方向走向B处,乙从A处出发沿南偏西30°方向走到C处,则∠BAC的度数是 ( )
A. B. C. D.
2.如图,这是一个正方体侧面展开图,如果E在上面那么在下面的字母是( )
A.C B.D C.F D.B
3.用圆规比较图中的四条线段,其中最长的是( )
A.BC B.AB C.DA D.CD
4.时钟上的分针匀速旋转一周需要60分钟,则经过10分钟,分针旋转了( ).
A.10° B.20° C.30° D.60°
5.图1的直角柱由2个正三角形底面和3个矩形侧面组成,其中正三角形面积为a,矩形面积为b.若将4个图1的直角柱紧密堆叠成图2的直角柱,则图2中直角柱的表面积为何?( )
A. B. C. D.
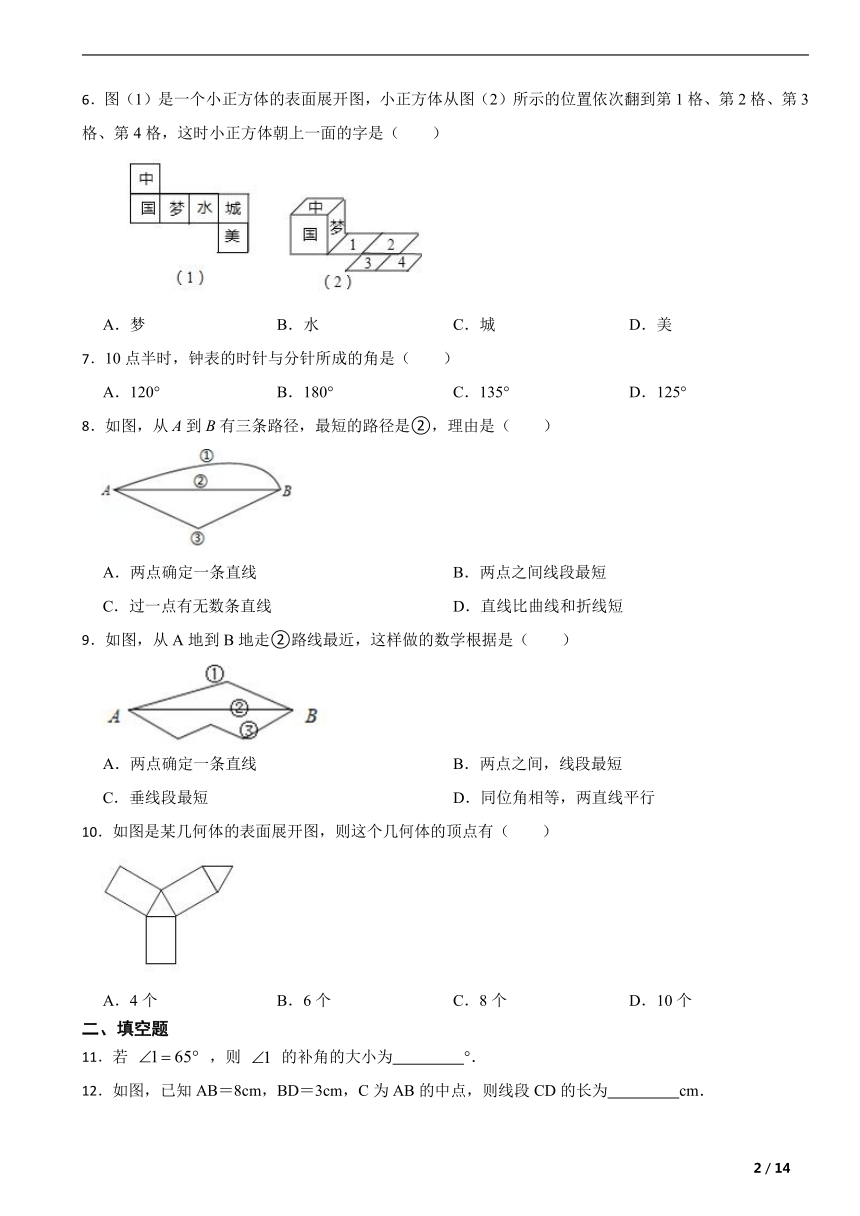
6.图(1)是一个小正方体的表面展开图,小正方体从图(2)所示的位置依次翻到第1格、第2格、第3格、第4格,这时小正方体朝上一面的字是( )
A.梦 B.水 C.城 D.美
7.10点半时,钟表的时针与分针所成的角是( )
A.120° B.180° C.135° D.125°
8.如图,从A到B有三条路径,最短的路径是②,理由是( )
A.两点确定一条直线 B.两点之间线段最短
C.过一点有无数条直线 D.直线比曲线和折线短
9.如图,从A地到B地走②路线最近,这样做的数学根据是( )
A.两点确定一条直线 B.两点之间,线段最短
C.垂线段最短 D.同位角相等,两直线平行
10.如图是某几何体的表面展开图,则这个几何体的顶点有( )
A.4个 B.6个 C.8个 D.10个
二、填空题
11.若 ,则 的补角的大小为 °.
12.如图,已知AB=8cm,BD=3cm,C为AB的中点,则线段CD的长为 cm.
13.如图所示,一个长方体的长为4cm,宽为3cm,高为5cm.则长方体所有棱长的和为 ;长方体的表面积为 .
14.在时钟的钟面上,8:30 时的分针与时针夹角是 度.
三、解答题
15.如图,O是直线上一点,,求的度数.
16.如图,已知C点为线段AB的中点,D点为BC的中点,AB=10cm,求AD的长度.
17.已知:如图,AD 是∠BAC 的平分线,∠B=∠EAC,ED⊥AD 于 D.
求证:DE 平分∠AEB.
18.如图,已知OD平分∠AOB,射线OC在∠AOD内,∠BOC=2∠AOC,∠AOB=114°.求∠COD的度数.
四、综合题
19.如图,已知平面内三点 ,按要求完成下列问题:
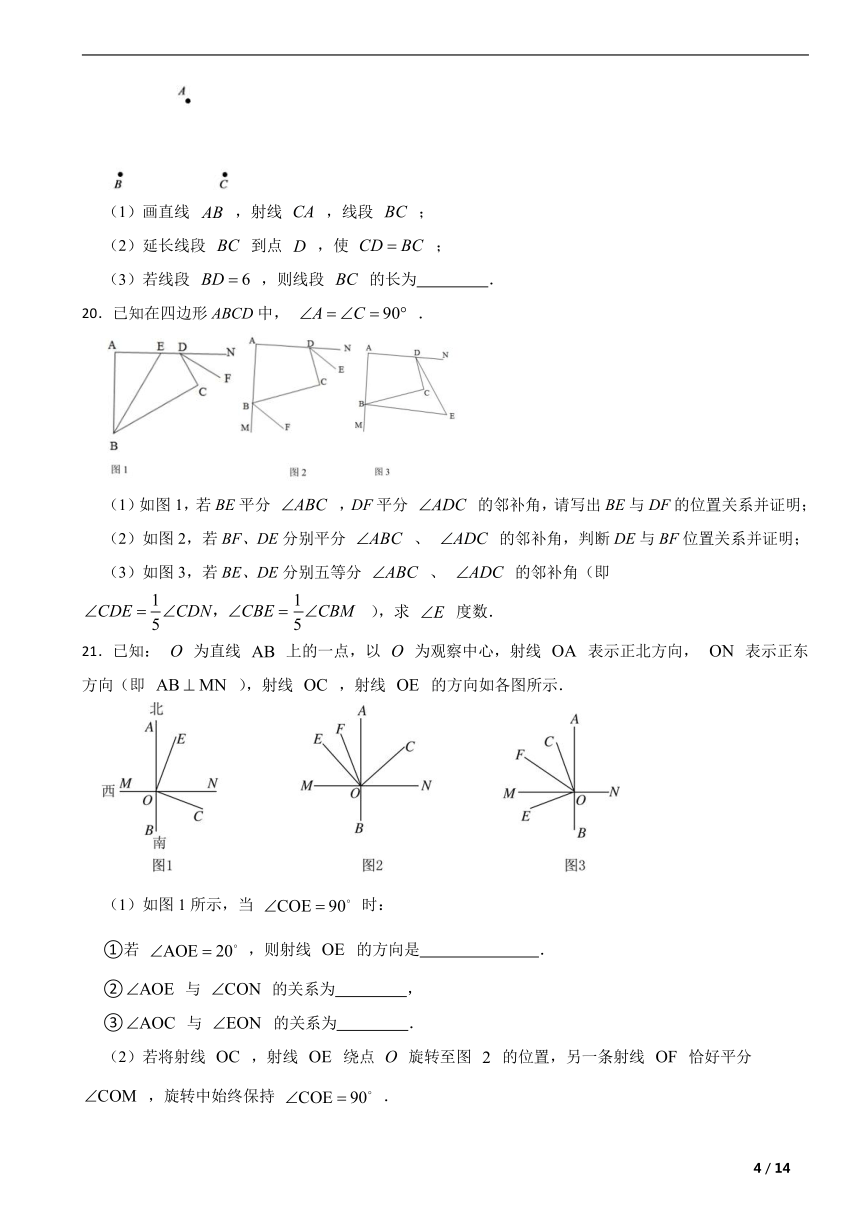
(1)画直线 ,射线 ,线段 ;
(2)延长线段 到点 ,使 ;
(3)若线段 ,则线段 的长为 .
20.已知在四边形ABCD中, .
(1)如图1,若BE平分 ,DF平分 的邻补角,请写出BE与DF的位置关系并证明;
(2)如图2,若BF、DE分别平分 、 的邻补角,判断DE与BF位置关系并证明;
(3)如图3,若BE、DE分别五等分 、 的邻补角(即 ),求 度数.
21.已知: 为直线 上的一点,以 为观察中心,射线 表示正北方向, 表示正东方向(即 ),射线 ,射线 的方向如各图所示.
(1)如图1所示,当 时:
①若 ,则射线 的方向是 .
② 与 的关系为 ,
③ 与 的关系为 .
(2)若将射线 ,射线 绕点 旋转至图 的位置,另一条射线 恰好平分 ,旋转中始终保持 .
①若 ,则 度.
②若 ,则 (用含 的代数式表示).
(3)若将射线 ,射线 绕点 旋转至图 的位置,射线 仍然平分 ,旋转中始终保持 ,则 与 之间存在怎样的数量关系,并说明理由.
22.已知长方形的长为4 cm.宽为3 cm,将其绕它的一边所在的直线旋转一周,得到一个几何体.
(1)求此几何体的体积;
(2)求此几何体的表面积.(结果保留π)
23.如图1, 是直线 上的点,线段 ,点 分别是线段 的中点.
(1)求线段 的长;
(2)若 ,点 在直线 上, ,求线段 的长;
(3)若 ,点 在直线 上, ,请直接写出线段 的长 .(用含 的式子表示)
答案解析部分
1.【答案】B
【解析】【解答】解:由方向角的意义可知,∠NAB=60°,∠SAC=30°,
∴∠BAE=90°-60°=30°,
∴∠BAC=∠BAE+∠EAS+∠SAC
=30°+90°+30°
=150°,
故答案为:B.
【分析】先求出∠BAE=90°-∠BAN=30°,再利用∠BAC=∠BAE+∠EAS+∠SAC即可求解.
2.【答案】D
【解析】【解答】正方体的表面展开图,相对的面之间一定相隔一个正方形,
如果E在上面,那么在下面的字母是B.
故答案为:D.
【分析】根据正方体的展开图的特征“相对的面之间一定相隔一个正方形”可求解.
3.【答案】A
【解析】【解答】解:通过用圆规比较图中的四条线段,其中最长的是BC;
故答案为:A.
【分析】用圆规量出四条线段,再进行比较即可.
4.【答案】D
【解析】【解答】解:∵时钟上的分针匀速旋转一周的度数为360°,时钟上的分针匀速旋转一周需要60分钟,
则时钟上的分针匀速旋转一分钟时的度数为:360÷60=6°,
那么10分钟,分针旋转了10×6°=60°,
故答案为:D.
【分析】先求出时钟上的分针匀速旋转一分钟时的度数为6°,再求10分钟分针旋转的度数就简单了.
5.【答案】C
【解析】【解答】解: ∵正三角形面积为a,矩形面积为b,
∴图2中直角柱的表面积=2×4a+6b=8a+6b,
故答案为:C.
【分析】图2的直角柱一个底边的面积为4a,两个底面的面积为2×4a,其侧面的面积为6b,根据该几何体表面积=两底面面积+侧面积列出代数值,再化简即可。
6.【答案】A
【解析】【解答】解:第一次翻转梦在下面,第二次翻转中在下面,第三次翻转国在下面,第四次翻转城在下面,
城与梦相对,
故选:A.
【分析】根据两个面相隔一个面是对面,再根据翻转的规律,可得答案.
7.【答案】C
【解析】【解答】解:10:30如下图所示,
∵ 时针在钟面上每分钟转0.5°,分针每分钟转6°,
∴ 钟表上10点30分,时针与分针的夹角可以看成 4 X 30°+0.5°x 30= 135°
故答案为:C.
【分析】因为钟表上的刻度是把一个圆平均分成了12等份,每一份是30°,借助图形,找出时针和分针之间相差的大格数,用大格数乘30°即可.
8.【答案】B
【解析】【解答】解:根据两点之间线段最短,即可得到最短的路径为②。
故答案为:B.
【分析】根据两点之间线段最短的定理进行判断得到答案即可。
9.【答案】B
【解析】【解答】解:从A地到B地走②条路线最近,它根据的是两点之间线段最短.
故选:B.
【分析】由题意从A到B,肯定要尽量缩短两地之间的里程,就用到两点间线段最短定理.
10.【答案】B
【解析】【解答】解:由图可知,这是一个三棱柱的表面展开图,它的顶点数是6个.
故选:B.
【分析】由图可知,这是一个三棱柱的表面展开图,据此可知它的顶点数.
11.【答案】115
【解析】【解答】 的补角= - = - =
故答案为:115.
【分析】如果两个角的和等于180°,那么这两个角叫做互为补角,据此解答即可.
12.【答案】1
【解析】【解答】解:∵C为AB的中点,AB=8cm,
∴BC= AB= ×8=4(cm),
∵BD=3cm,
∴CD=BC﹣BD=4﹣3=1(cm),
则CD的长为1cm;
故答案为:1.
【分析】先根据中点定义求BC的长,再利用线段的差求CD的长.
13.【答案】48cm;94cm2
【解析】【解答】解:长方体的长、宽、高分别为4cm,3cm,5cm,
(Ⅰ)这个长方体的棱长总和为4×(4+3+5)=48cm,
故长方体所有棱长的和为48cm.
(Ⅱ)表面积2×(4×3+4×5+3×5)=2×47=94cm2.
故长方体的表面积为94cm2.
故答案为:48cm;94cm2.
【分析】(1)长方体的棱长总和=4(长+宽+高);(2)长方体的表面积=2(长×宽+长×高+宽×高),把相关数字代入即可.
14.【答案】75
【解析】【解答】解:2.5×30°=75°,
故答案为:75.
【分析】根据钟面上每两个刻度之间是30°,8点半时,钟面上分针与时针的夹角是两个半刻度,可得答案。
15.【答案】解:由题意可知,是平角,,
所以
.
【解析】【分析】先求出 是平角,, 再计算求解即可。
16.【答案】解:∵C点为线段AB的中点,D点为BC的中点,AB=10cm,
∴AC=CB= AB=5cm,CD= BC=2.5cm,
∴AD=AC+CD=5+2.5=7.5cm.
【解析】【分析】已知C点为线段AB的中点,D点为BC的中点,AB=10cm,根据线段中点的定义可得AC=CB= AB=5cm,CD= BC=2.5cm,由AD=AC+CD即可求得AD的长度.
17.【答案】证明:延长 AD 交 BC 于 F,
∵AD 是∠BAC 的平分线,
∴∠BAD=∠CAD,
∵∠DFE=∠B+∠BAD,∠DAE=∠EAC+∠CAD,
∵∠B=∠EAC,
∴∠DFE=∠DAE,
∴AE=FE,
∵ED⊥AD,
∴ED 平分∠AEB.
【解析】【分析】延长 AD 交 BC 于 F,由AD 是∠BAC 的平分线,∠B=∠EAC,得出∠BAD=∠CAD,AE=FE,由ED⊥AD,根据三线合一的性质,即可证得ED 平分∠AEB.
18.【答案】解:∵OD平分∠AOB,∠AOB=114°,∴∠AOD=∠BOD=∠AOB=57°.∵∠BOC=2∠AOC,∠AOB=114°,∴∠AOC=∠AOB=380.∴∠COD=∠AOD﹣∠AOC=57°﹣38°=19°.
【解析】【分析】根据OD平分∠AOB,射线OC在∠AOD内,∠BOC=2∠AOC,∠AOB=114°,可以求得∠AOC、∠AOD的度数,从而可以求得∠COD的度数.
19.【答案】(1)解:如图;
(2)解:如图;
(3)3
【解析】【解答】(3)∵ , ,
∴BC= BD=3,
故答案为:3.
【分析】(1)根据直线、射线、线段的定义即可画出直线AB,射线CA,线段BC;
(2)根据线段定义即可延长线段BC到点D,使得CD=BC;
(3)根据线段BD=6,可得线段BC的长。
20.【答案】(1)解: .
证明:延长BE、FD交于G.在四边形ABCD中,
, ,
.
, .
平分 ,DF平分 ,
, ,
,
∵∠ABE+∠AEB=90°,∠AEB=∠DEG,∠FDN=∠EDG,
∴∠DEG+∠EDG=90°,
∴∠EGD=90°,即BE⊥DF.
(2)解: .
证明:连接DB.
, .
又 , .
、DF平分 、 的邻补角,
, ,
.
在 中,
,
,
, .
(3)解:延长DC交BE于H.
由(1)得:
.
、DE分别五等分 、 的邻补角,
,
由三角形的外角性质得,
, ,
,
.
【解析】【分析】(1)延长BE、FD交于G.在四边形ABCD中,想办法证明∠DEG+∠EDG=90°,即可;
(2),连接DB.证明出即可;
(3)利用结论: ,即可解决问题。
21.【答案】(1)北偏东20°;相等;互补
(2)24°;2β
(3)解:∵∠CON=180°-∠COM=180°-2∠MOF.
又∠AOF=90°-∠MOF,∴2∠AOF=180°-2∠MOF.
∴∠CON=2∠AOF.
【解析】【解答】解:(1)①北偏东20°
②∵由题意知,∠AOE+∠EON=90°,∠NOC+∠EON=90°,
∴∠AOE=∠CON.
③由题意知,∠BOC+∠NOC=90°,∠NOC+∠EON=90°,
∴∠BOC=∠EON,
又∠AOC+∠BOC=180°,
∴∠AOC+∠EON=180°.
故答案为:①北偏东20°;②相等;③互补.
( 2 )①由题意知,∠AOC+∠AOE=90°,∠MOE+∠AOE=90°,
∴∠AOC=∠MOE,
又OF为∠COM的角平分线,
∴∠COF=∠MOF,
∴∠COF-∠AOC=∠MOF-∠MOE,
∴∠AOF=∠EOF=24°.
②由①知,∠AOF=∠EOF=β,
∴∠CON=∠AOE=2∠AOF=2β.
故答案为:①24°;②2β.
【分析】(1)①根据方向角的定义即可求解;②根据同角的余角相等即可得出结论;③先根据同角的余角相等得出∠EON=∠BOC,再根据两角互补的定义即可得出结果.(2)①根据同角的余角可知∠AOC=∠MOE,又根据角平分线的定义可得∠COF=∠MOF,两式相减即可得出结果.②由①知∠AOF=∠EOF=β,又由∠CON=∠AOE即可得出结果.(3)根据角的和差,以及角平分线的定义即可求解.
22.【答案】(1)解:长方形绕一边旋转一周,得圆柱.情况①:π×32×4=36π(cm3);
情况②:π×42×3=48π(cm3)
(2)解:情况①:π×3×2×4+π×32×2=24π+18π=42π(cm2);
情况②:π×4×2×3+π×42×2=24π+32π=56π(cm2)
【解析】【分析】(1)长方形绕一边旋转一周后得到一个圆柱体,根据绕长旋转一周和绕宽旋转一周,由长长方形的长和宽的值,求出圆柱体的体积;(2)根据绕长旋转一周,圆柱体的底面半径是宽的值,绕宽旋转一周,圆柱体的底面半径是长的值,求出圆柱体的表面积.
23.【答案】(1)解:∵点 分别是线段 的中点,
∴ ,
∴
(2)解:由(1)知由 ,
当点 在点 左侧时,
,
当点 在点 右侧时,
;
∴OE的长为8cm或18cm.
(3) 或 或
【解析】【解答】解:(3)∵E为BC中点,
∴BE= ,
当点O在点A左边时,OE=16- +b,
当点O在线段AE上时,OE=16- -b,
当点O在线段BE上时,OE= -(16-b)=b+ -16,
当点O在B点右边时,OE=b+ -16,
故答案为: 或 或 .
【分析】(1)由中点的定义可得DC= AC,BE= BC,根据DE=DC+CE即可得答案;(2)由中点定义可求出BE的长,分别讨论点O在点A左边和右边两种情况,根据线段间的和差关系求出OE的长即可;(3)分别讨论点O在点A左边、线段AE上、线段BE上和点B右边的情况,根据线段的和差关系即可得答案.
1 / 1
一、单选题
1.如图,甲从A处出发沿北偏东60°方向走向B处,乙从A处出发沿南偏西30°方向走到C处,则∠BAC的度数是 ( )
A. B. C. D.
2.如图,这是一个正方体侧面展开图,如果E在上面那么在下面的字母是( )
A.C B.D C.F D.B
3.用圆规比较图中的四条线段,其中最长的是( )
A.BC B.AB C.DA D.CD
4.时钟上的分针匀速旋转一周需要60分钟,则经过10分钟,分针旋转了( ).
A.10° B.20° C.30° D.60°
5.图1的直角柱由2个正三角形底面和3个矩形侧面组成,其中正三角形面积为a,矩形面积为b.若将4个图1的直角柱紧密堆叠成图2的直角柱,则图2中直角柱的表面积为何?( )
A. B. C. D.
6.图(1)是一个小正方体的表面展开图,小正方体从图(2)所示的位置依次翻到第1格、第2格、第3格、第4格,这时小正方体朝上一面的字是( )
A.梦 B.水 C.城 D.美
7.10点半时,钟表的时针与分针所成的角是( )
A.120° B.180° C.135° D.125°
8.如图,从A到B有三条路径,最短的路径是②,理由是( )
A.两点确定一条直线 B.两点之间线段最短
C.过一点有无数条直线 D.直线比曲线和折线短
9.如图,从A地到B地走②路线最近,这样做的数学根据是( )
A.两点确定一条直线 B.两点之间,线段最短
C.垂线段最短 D.同位角相等,两直线平行
10.如图是某几何体的表面展开图,则这个几何体的顶点有( )
A.4个 B.6个 C.8个 D.10个
二、填空题
11.若 ,则 的补角的大小为 °.
12.如图,已知AB=8cm,BD=3cm,C为AB的中点,则线段CD的长为 cm.
13.如图所示,一个长方体的长为4cm,宽为3cm,高为5cm.则长方体所有棱长的和为 ;长方体的表面积为 .
14.在时钟的钟面上,8:30 时的分针与时针夹角是 度.
三、解答题
15.如图,O是直线上一点,,求的度数.
16.如图,已知C点为线段AB的中点,D点为BC的中点,AB=10cm,求AD的长度.
17.已知:如图,AD 是∠BAC 的平分线,∠B=∠EAC,ED⊥AD 于 D.
求证:DE 平分∠AEB.
18.如图,已知OD平分∠AOB,射线OC在∠AOD内,∠BOC=2∠AOC,∠AOB=114°.求∠COD的度数.
四、综合题
19.如图,已知平面内三点 ,按要求完成下列问题:
(1)画直线 ,射线 ,线段 ;
(2)延长线段 到点 ,使 ;
(3)若线段 ,则线段 的长为 .
20.已知在四边形ABCD中, .
(1)如图1,若BE平分 ,DF平分 的邻补角,请写出BE与DF的位置关系并证明;
(2)如图2,若BF、DE分别平分 、 的邻补角,判断DE与BF位置关系并证明;
(3)如图3,若BE、DE分别五等分 、 的邻补角(即 ),求 度数.
21.已知: 为直线 上的一点,以 为观察中心,射线 表示正北方向, 表示正东方向(即 ),射线 ,射线 的方向如各图所示.
(1)如图1所示,当 时:
①若 ,则射线 的方向是 .
② 与 的关系为 ,
③ 与 的关系为 .
(2)若将射线 ,射线 绕点 旋转至图 的位置,另一条射线 恰好平分 ,旋转中始终保持 .
①若 ,则 度.
②若 ,则 (用含 的代数式表示).
(3)若将射线 ,射线 绕点 旋转至图 的位置,射线 仍然平分 ,旋转中始终保持 ,则 与 之间存在怎样的数量关系,并说明理由.
22.已知长方形的长为4 cm.宽为3 cm,将其绕它的一边所在的直线旋转一周,得到一个几何体.
(1)求此几何体的体积;
(2)求此几何体的表面积.(结果保留π)
23.如图1, 是直线 上的点,线段 ,点 分别是线段 的中点.
(1)求线段 的长;
(2)若 ,点 在直线 上, ,求线段 的长;
(3)若 ,点 在直线 上, ,请直接写出线段 的长 .(用含 的式子表示)
答案解析部分
1.【答案】B
【解析】【解答】解:由方向角的意义可知,∠NAB=60°,∠SAC=30°,
∴∠BAE=90°-60°=30°,
∴∠BAC=∠BAE+∠EAS+∠SAC
=30°+90°+30°
=150°,
故答案为:B.
【分析】先求出∠BAE=90°-∠BAN=30°,再利用∠BAC=∠BAE+∠EAS+∠SAC即可求解.
2.【答案】D
【解析】【解答】正方体的表面展开图,相对的面之间一定相隔一个正方形,
如果E在上面,那么在下面的字母是B.
故答案为:D.
【分析】根据正方体的展开图的特征“相对的面之间一定相隔一个正方形”可求解.
3.【答案】A
【解析】【解答】解:通过用圆规比较图中的四条线段,其中最长的是BC;
故答案为:A.
【分析】用圆规量出四条线段,再进行比较即可.
4.【答案】D
【解析】【解答】解:∵时钟上的分针匀速旋转一周的度数为360°,时钟上的分针匀速旋转一周需要60分钟,
则时钟上的分针匀速旋转一分钟时的度数为:360÷60=6°,
那么10分钟,分针旋转了10×6°=60°,
故答案为:D.
【分析】先求出时钟上的分针匀速旋转一分钟时的度数为6°,再求10分钟分针旋转的度数就简单了.
5.【答案】C
【解析】【解答】解: ∵正三角形面积为a,矩形面积为b,
∴图2中直角柱的表面积=2×4a+6b=8a+6b,
故答案为:C.
【分析】图2的直角柱一个底边的面积为4a,两个底面的面积为2×4a,其侧面的面积为6b,根据该几何体表面积=两底面面积+侧面积列出代数值,再化简即可。
6.【答案】A
【解析】【解答】解:第一次翻转梦在下面,第二次翻转中在下面,第三次翻转国在下面,第四次翻转城在下面,
城与梦相对,
故选:A.
【分析】根据两个面相隔一个面是对面,再根据翻转的规律,可得答案.
7.【答案】C
【解析】【解答】解:10:30如下图所示,
∵ 时针在钟面上每分钟转0.5°,分针每分钟转6°,
∴ 钟表上10点30分,时针与分针的夹角可以看成 4 X 30°+0.5°x 30= 135°
故答案为:C.
【分析】因为钟表上的刻度是把一个圆平均分成了12等份,每一份是30°,借助图形,找出时针和分针之间相差的大格数,用大格数乘30°即可.
8.【答案】B
【解析】【解答】解:根据两点之间线段最短,即可得到最短的路径为②。
故答案为:B.
【分析】根据两点之间线段最短的定理进行判断得到答案即可。
9.【答案】B
【解析】【解答】解:从A地到B地走②条路线最近,它根据的是两点之间线段最短.
故选:B.
【分析】由题意从A到B,肯定要尽量缩短两地之间的里程,就用到两点间线段最短定理.
10.【答案】B
【解析】【解答】解:由图可知,这是一个三棱柱的表面展开图,它的顶点数是6个.
故选:B.
【分析】由图可知,这是一个三棱柱的表面展开图,据此可知它的顶点数.
11.【答案】115
【解析】【解答】 的补角= - = - =
故答案为:115.
【分析】如果两个角的和等于180°,那么这两个角叫做互为补角,据此解答即可.
12.【答案】1
【解析】【解答】解:∵C为AB的中点,AB=8cm,
∴BC= AB= ×8=4(cm),
∵BD=3cm,
∴CD=BC﹣BD=4﹣3=1(cm),
则CD的长为1cm;
故答案为:1.
【分析】先根据中点定义求BC的长,再利用线段的差求CD的长.
13.【答案】48cm;94cm2
【解析】【解答】解:长方体的长、宽、高分别为4cm,3cm,5cm,
(Ⅰ)这个长方体的棱长总和为4×(4+3+5)=48cm,
故长方体所有棱长的和为48cm.
(Ⅱ)表面积2×(4×3+4×5+3×5)=2×47=94cm2.
故长方体的表面积为94cm2.
故答案为:48cm;94cm2.
【分析】(1)长方体的棱长总和=4(长+宽+高);(2)长方体的表面积=2(长×宽+长×高+宽×高),把相关数字代入即可.
14.【答案】75
【解析】【解答】解:2.5×30°=75°,
故答案为:75.
【分析】根据钟面上每两个刻度之间是30°,8点半时,钟面上分针与时针的夹角是两个半刻度,可得答案。
15.【答案】解:由题意可知,是平角,,
所以
.
【解析】【分析】先求出 是平角,, 再计算求解即可。
16.【答案】解:∵C点为线段AB的中点,D点为BC的中点,AB=10cm,
∴AC=CB= AB=5cm,CD= BC=2.5cm,
∴AD=AC+CD=5+2.5=7.5cm.
【解析】【分析】已知C点为线段AB的中点,D点为BC的中点,AB=10cm,根据线段中点的定义可得AC=CB= AB=5cm,CD= BC=2.5cm,由AD=AC+CD即可求得AD的长度.
17.【答案】证明:延长 AD 交 BC 于 F,
∵AD 是∠BAC 的平分线,
∴∠BAD=∠CAD,
∵∠DFE=∠B+∠BAD,∠DAE=∠EAC+∠CAD,
∵∠B=∠EAC,
∴∠DFE=∠DAE,
∴AE=FE,
∵ED⊥AD,
∴ED 平分∠AEB.
【解析】【分析】延长 AD 交 BC 于 F,由AD 是∠BAC 的平分线,∠B=∠EAC,得出∠BAD=∠CAD,AE=FE,由ED⊥AD,根据三线合一的性质,即可证得ED 平分∠AEB.
18.【答案】解:∵OD平分∠AOB,∠AOB=114°,∴∠AOD=∠BOD=∠AOB=57°.∵∠BOC=2∠AOC,∠AOB=114°,∴∠AOC=∠AOB=380.∴∠COD=∠AOD﹣∠AOC=57°﹣38°=19°.
【解析】【分析】根据OD平分∠AOB,射线OC在∠AOD内,∠BOC=2∠AOC,∠AOB=114°,可以求得∠AOC、∠AOD的度数,从而可以求得∠COD的度数.
19.【答案】(1)解:如图;
(2)解:如图;
(3)3
【解析】【解答】(3)∵ , ,
∴BC= BD=3,
故答案为:3.
【分析】(1)根据直线、射线、线段的定义即可画出直线AB,射线CA,线段BC;
(2)根据线段定义即可延长线段BC到点D,使得CD=BC;
(3)根据线段BD=6,可得线段BC的长。
20.【答案】(1)解: .
证明:延长BE、FD交于G.在四边形ABCD中,
, ,
.
, .
平分 ,DF平分 ,
, ,
,
∵∠ABE+∠AEB=90°,∠AEB=∠DEG,∠FDN=∠EDG,
∴∠DEG+∠EDG=90°,
∴∠EGD=90°,即BE⊥DF.
(2)解: .
证明:连接DB.
, .
又 , .
、DF平分 、 的邻补角,
, ,
.
在 中,
,
,
, .
(3)解:延长DC交BE于H.
由(1)得:
.
、DE分别五等分 、 的邻补角,
,
由三角形的外角性质得,
, ,
,
.
【解析】【分析】(1)延长BE、FD交于G.在四边形ABCD中,想办法证明∠DEG+∠EDG=90°,即可;
(2),连接DB.证明出即可;
(3)利用结论: ,即可解决问题。
21.【答案】(1)北偏东20°;相等;互补
(2)24°;2β
(3)解:∵∠CON=180°-∠COM=180°-2∠MOF.
又∠AOF=90°-∠MOF,∴2∠AOF=180°-2∠MOF.
∴∠CON=2∠AOF.
【解析】【解答】解:(1)①北偏东20°
②∵由题意知,∠AOE+∠EON=90°,∠NOC+∠EON=90°,
∴∠AOE=∠CON.
③由题意知,∠BOC+∠NOC=90°,∠NOC+∠EON=90°,
∴∠BOC=∠EON,
又∠AOC+∠BOC=180°,
∴∠AOC+∠EON=180°.
故答案为:①北偏东20°;②相等;③互补.
( 2 )①由题意知,∠AOC+∠AOE=90°,∠MOE+∠AOE=90°,
∴∠AOC=∠MOE,
又OF为∠COM的角平分线,
∴∠COF=∠MOF,
∴∠COF-∠AOC=∠MOF-∠MOE,
∴∠AOF=∠EOF=24°.
②由①知,∠AOF=∠EOF=β,
∴∠CON=∠AOE=2∠AOF=2β.
故答案为:①24°;②2β.
【分析】(1)①根据方向角的定义即可求解;②根据同角的余角相等即可得出结论;③先根据同角的余角相等得出∠EON=∠BOC,再根据两角互补的定义即可得出结果.(2)①根据同角的余角可知∠AOC=∠MOE,又根据角平分线的定义可得∠COF=∠MOF,两式相减即可得出结果.②由①知∠AOF=∠EOF=β,又由∠CON=∠AOE即可得出结果.(3)根据角的和差,以及角平分线的定义即可求解.
22.【答案】(1)解:长方形绕一边旋转一周,得圆柱.情况①:π×32×4=36π(cm3);
情况②:π×42×3=48π(cm3)
(2)解:情况①:π×3×2×4+π×32×2=24π+18π=42π(cm2);
情况②:π×4×2×3+π×42×2=24π+32π=56π(cm2)
【解析】【分析】(1)长方形绕一边旋转一周后得到一个圆柱体,根据绕长旋转一周和绕宽旋转一周,由长长方形的长和宽的值,求出圆柱体的体积;(2)根据绕长旋转一周,圆柱体的底面半径是宽的值,绕宽旋转一周,圆柱体的底面半径是长的值,求出圆柱体的表面积.
23.【答案】(1)解:∵点 分别是线段 的中点,
∴ ,
∴
(2)解:由(1)知由 ,
当点 在点 左侧时,
,
当点 在点 右侧时,
;
∴OE的长为8cm或18cm.
(3) 或 或
【解析】【解答】解:(3)∵E为BC中点,
∴BE= ,
当点O在点A左边时,OE=16- +b,
当点O在线段AE上时,OE=16- -b,
当点O在线段BE上时,OE= -(16-b)=b+ -16,
当点O在B点右边时,OE=b+ -16,
故答案为: 或 或 .
【分析】(1)由中点的定义可得DC= AC,BE= BC,根据DE=DC+CE即可得答案;(2)由中点定义可求出BE的长,分别讨论点O在点A左边和右边两种情况,根据线段间的和差关系求出OE的长即可;(3)分别讨论点O在点A左边、线段AE上、线段BE上和点B右边的情况,根据线段的和差关系即可得答案.
1 / 1
