2023--2024学年沪科版九年级上学期期末数学模拟押题试卷(安徽亳州适用)(含解析)
文档属性
| 名称 | 2023--2024学年沪科版九年级上学期期末数学模拟押题试卷(安徽亳州适用)(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 687.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-18 00:00:00 | ||
图片预览

文档简介
2023--2024学年沪科版九年级上学期期末数学模拟押题试卷(安徽亳州适用)
一、单选题
1.下列函数中属于二次函数的是( )
A. B.
C. D.
2.已知,则的值为( )
A. B. C. D.
3.如图1,在中,点P从点A出发向点C运动,设x表示线段的长,y表示线段的长,下列结论不正确的是( )
A. B. C. D.
4.如图是我们学过的反比例函数图象,它的函数解析式可能是( )
A. B. C. D.
5.下列说法正确的是( )
A.如果两个角相等,那么这两个角是对顶角
B.经过一点有且只有一条直线与已知直线平行
C.如果两条直线被第三条直线所截,那么内错角相等
D.联结直线外一点与直线上各点的所有线段中,垂线段最短
6.已知x+y=6,xy=4,则x2y+xy2的值为( )
A.12 B.-12 C.-24 D.24
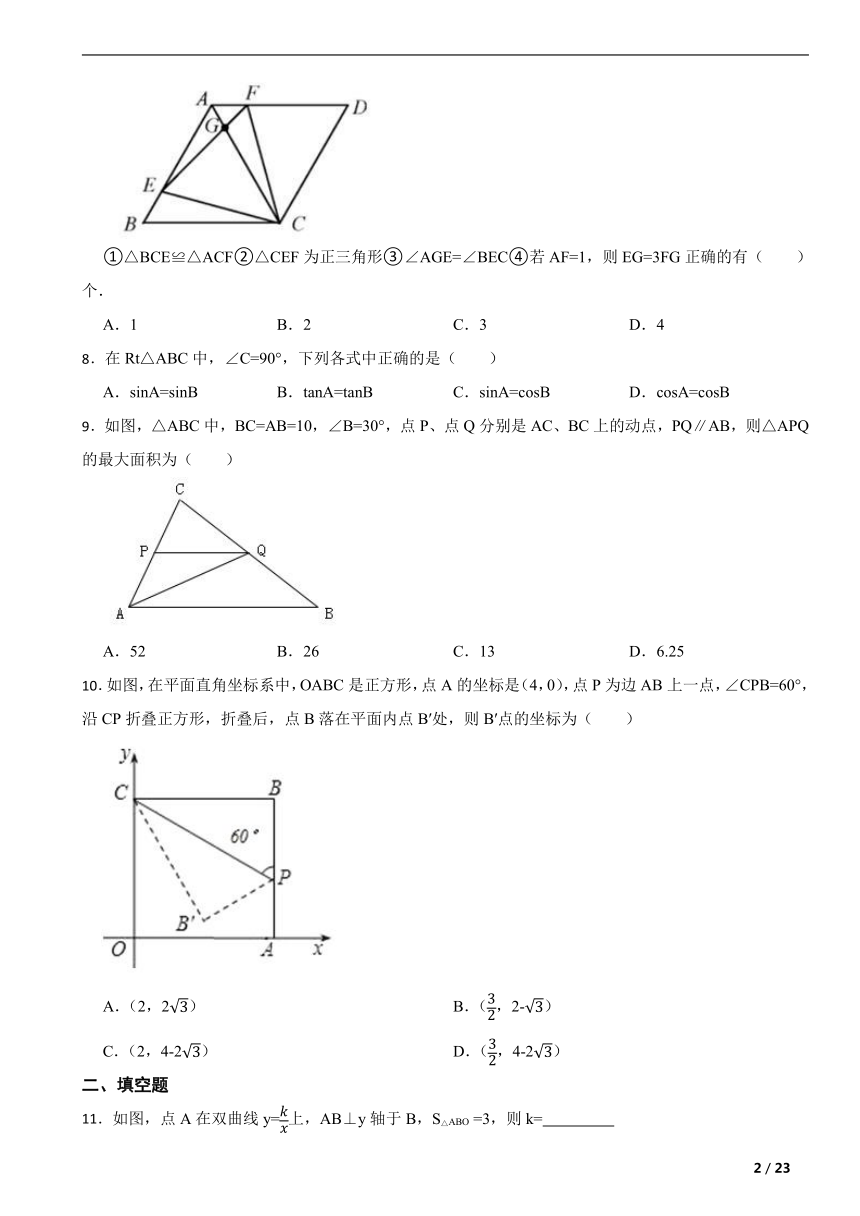
7.已知菱形ABCD,E、F是动点,边长为4,BE=AF,∠BAD=120°,则下列结论:
①△BCE≌△ACF②△CEF为正三角形③∠AGE=∠BEC④若AF=1,则EG=3FG正确的有( )个.
A.1 B.2 C.3 D.4
8.在Rt△ABC中,∠C=90°,下列各式中正确的是( )
A.sinA=sinB B.tanA=tanB C.sinA=cosB D.cosA=cosB
9.如图,△ABC中,BC=AB=10,∠B=30°,点P、点Q分别是AC、BC上的动点,PQ∥AB,则△APQ的最大面积为( )
A.52 B.26 C.13 D.6.25
10.如图,在平面直角坐标系中,OABC是正方形,点A的坐标是(4,0),点P为边AB上一点,∠CPB=60°,沿CP折叠正方形,折叠后,点B落在平面内点B′处,则B′点的坐标为( )
A.(2,2) B.(,2-)
C.(2,4-2) D.(,4-2)
二、填空题
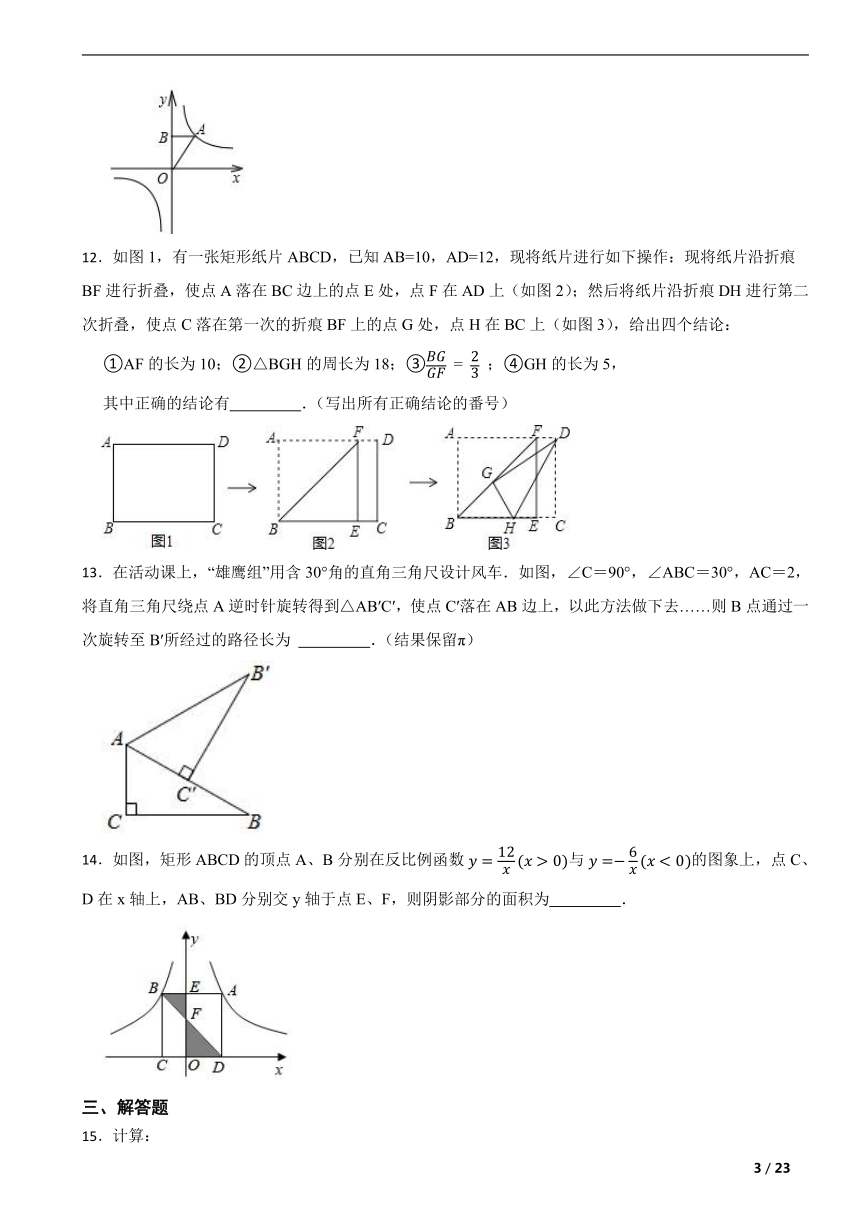
11.如图,点A在双曲线y=上,AB⊥y轴于B,S△ABO =3,则k=
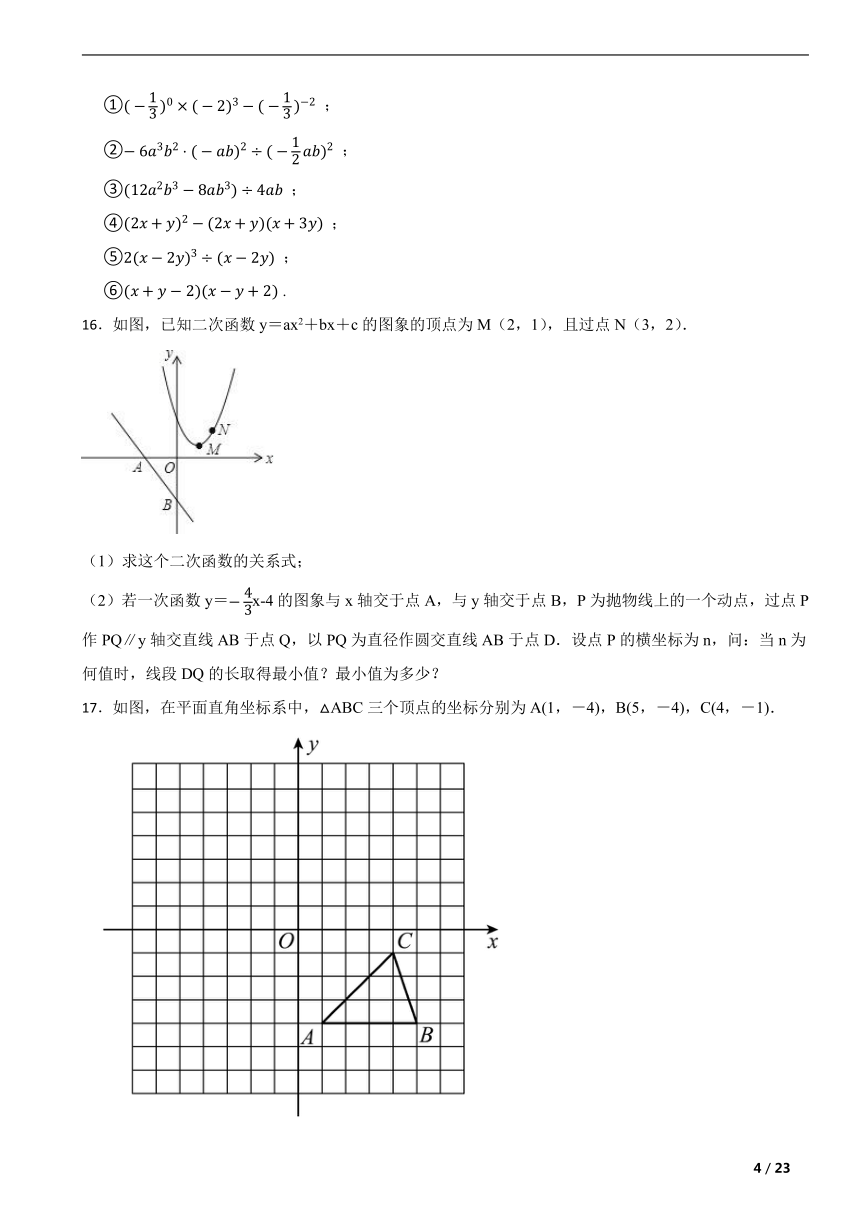
12.如图1,有一张矩形纸片ABCD,已知AB=10,AD=12,现将纸片进行如下操作:现将纸片沿折痕BF进行折叠,使点A落在BC边上的点E处,点F在AD上(如图2);然后将纸片沿折痕DH进行第二次折叠,使点C落在第一次的折痕BF上的点G处,点H在BC上(如图3),给出四个结论:
①AF的长为10;②△BGH的周长为18;③ = ;④GH的长为5,
其中正确的结论有 .(写出所有正确结论的番号)
13.在活动课上,“雄鹰组”用含30°角的直角三角尺设计风车.如图,∠C=90°,∠ABC=30°,AC=2,将直角三角尺绕点A逆时针旋转得到△AB′C′,使点C′落在AB边上,以此方法做下去……则B点通过一次旋转至B′所经过的路径长为 .(结果保留π)
14.如图,矩形ABCD的顶点A、B分别在反比例函数与的图象上,点C、D在x轴上,AB、BD分别交y轴于点E、F,则阴影部分的面积为 .
三、解答题
15.计算:
① ;
② ;
③ ;
④ ;
⑤ ;
⑥ .
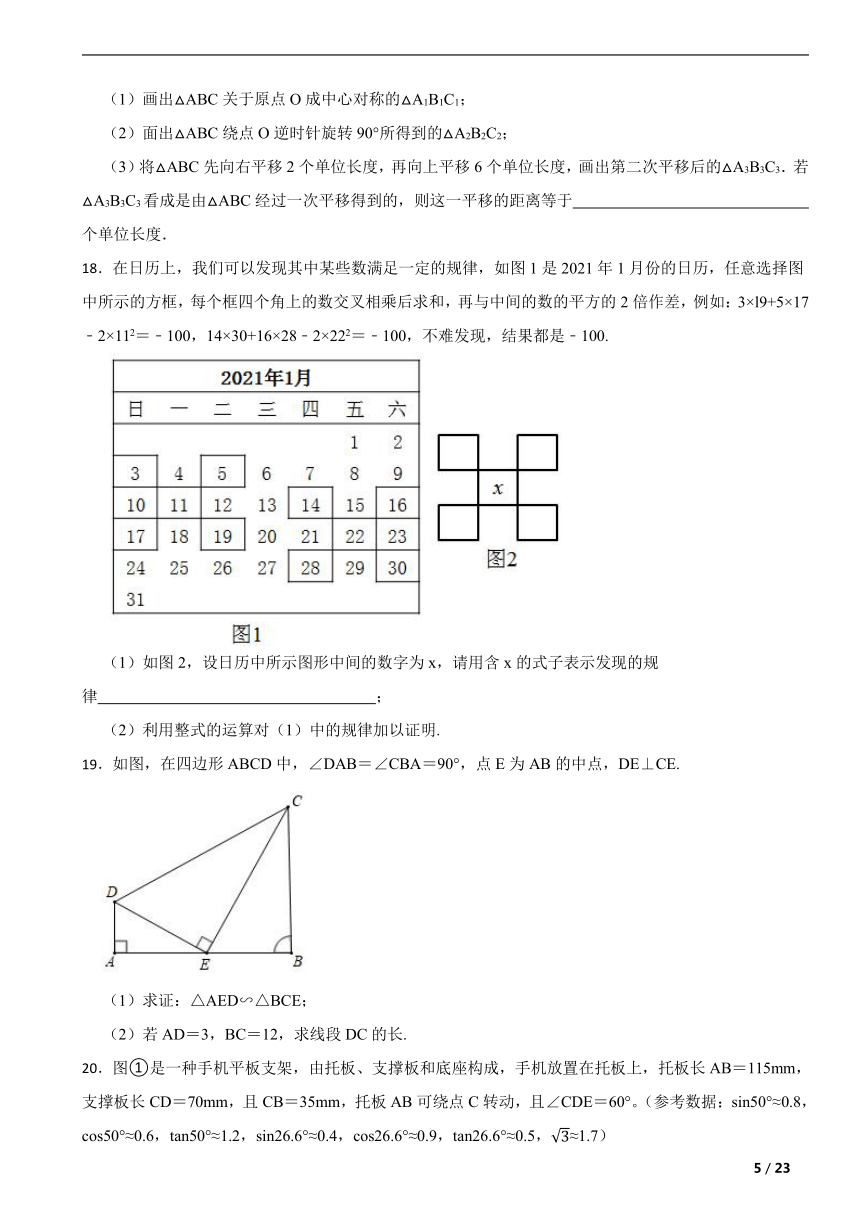
16.如图,已知二次函数y=ax2+bx+c的图象的顶点为M(2,1),且过点N(3,2).
(1)求这个二次函数的关系式;
(2)若一次函数y=x-4的图象与x轴交于点A,与y轴交于点B,P为抛物线上的一个动点,过点P作PQ∥y轴交直线AB于点Q,以PQ为直径作圆交直线AB于点D.设点P的横坐标为n,问:当n为何值时,线段DQ的长取得最小值?最小值为多少?
17.如图,在平面直角坐标系中,ABC三个顶点的坐标分别为A(1,-4),B(5,-4),C(4,-1).
(1)画出ABC关于原点O成中心对称的A1B1C1;
(2)面出ABC绕点O逆时针旋转90°所得到的A2B2C2;
(3)将ABC先向右平移2个单位长度,再向上平移6个单位长度,画出第二次平移后的A3B3C3.若A3B3C3看成是由ABC经过一次平移得到的,则这一平移的距离等于 个单位长度.
18.在日历上,我们可以发现其中某些数满足一定的规律,如图1是2021年1月份的日历,任意选择图中所示的方框,每个框四个角上的数交叉相乘后求和,再与中间的数的平方的2倍作差,例如:3×l9+5×17﹣2×112=﹣100,14×30+16×28﹣2×222=﹣100,不难发现,结果都是﹣100.
(1)如图2,设日历中所示图形中间的数字为x,请用含x的式子表示发现的规律 ;
(2)利用整式的运算对(1)中的规律加以证明.
19.如图,在四边形ABCD中,∠DAB=∠CBA=90°,点E为AB的中点,DE⊥CE.
(1)求证:△AED∽△BCE;
(2)若AD=3,BC=12,求线段DC的长.
20.图①是一种手机平板支架,由托板、支撑板和底座构成,手机放置在托板上,托板长AB=115mm,支撑板长CD=70mm,且CB=35mm,托板AB可绕点C转动,且∠CDE=60°。(参考数据:sin50°≈0.8,cos50°≈0.6,tan50°≈1.2,sin26.6°≈0.4,cos26.6°≈0.9,tan26.6°≈0.5,≈1.7)
(1)求点C到直线DE的距离(计算结果保留根号);
(2)若∠DCB=70°时,求点A到直线DE的距离(计算结果精确到个位);
(3)为了观看舒适,把(1)中∠DCB=70°调整为90°,再将CD绕点D逆时针旋转,使点B落在DE上,则CD旋转的度数为 .(直接写出结果)
21.如图,在平面直角坐标系中,一次函数的图象与y轴交于点(0,4),与直线在第四象限相交于点B,连接OB,的面积为6.
(1)求点B的坐标及直线AB的解析式;
(2)已知点M在直线AB右侧,且△MAB是以AB为直角边的等腰直角三角形.请求出符合条件的点M的坐标.
22.阅读:我们约定,在平面直角坐标系中,经过某点且平行于坐标轴或平行于两坐标轴夹角平分线的直线,叫该点的“特征线”.例如,点M(1,3)的特征线有:x=1,y=3,y=x+2,y=﹣x+4.
问题与探究:如图,在平面直角坐标系中有正方形OABC,点B在第一象限,A、C分别在x轴和y轴上,抛物线 经过B、C两点,顶点D在正方形内部.
(1)直接写出点D(m,n)所有的特征线;
(2)若点D有一条特征线是y=x+1,求此抛物线的解析式;
(3)点P是AB边上除点A外的任意一点,连接OP,将△OAP沿着OP折叠,点A落在点A′的位置,当点A′在平行于坐标轴的D点的特征线上时,满足(2)中条件的抛物线向下平移多少距离,其顶点落在OP上?
23.在平面直角坐标系中,二次函数 的图象与 轴交于A(-3,0),B(1,0)两点,与y轴交于点C.
(1)求这个二次函数的解析式;
(2)点P是直线AC上方的抛物线上一动点,是否存在点P,使△ACP的面积最大?若存在,求出点P的坐标;若不存在,说明理由;
(3)点Q是直线AC上方的抛物线上一动点,过点Q作QE垂直于 轴,垂足为E.是否存在点Q,使以点B、Q、E为顶点的三角形与△AOC相似?若存在,直接写出点Q的坐标;若不存在,说明理由;
答案解析部分
1.【答案】A
【解析】【解答】 解:A、是二次函数,A符合题意;
B:分母含有自变量,不是二次函数,B不符合题意;
C:自变量的次数是3次,不是二次函数,C不符合题意;
D:化简后自变量最高次数是1,不是二次函数,D不符合题意.
故答案为:A.
【分析】根据二次函数的定义对选项逐一进行判断即可求解.
2.【答案】C
【解析】【解答】解:∵,
∴,
∴,
故答案为:C.
【分析】由得,然后代入化简即可.
3.【答案】C
【解析】【解答】解:当点P在A处时,即当AP=0时,BP=AB.
当点P到AC边的高BH的位置时,AH=1,此时BP最小,BH=;
当AP=4时,点P对应图2末端,此时AC=4,HC=AC-AH=4-1=3,
∴BC=.
∵22+()2=42,
∴AB2+BC2=AC2,
∴∠ABC=90°,
∴tan∠BAP=.
故答案为:C.
【分析】当点P在A处时,即当AP=0时,BP=AB.,当点P到AC边的高BH的位置时,AH=1,此时BP最小,由勾股定理可得BH,当AP=4时,有AC=4,HC=AC-AH=4-1=3,由勾股定理可得BC,根据勾股定理逆定理知△ABC为直角三角形且∠ABC=90°,利用三角函数的概念可得tan∠BAP的值,据此判断.
4.【答案】B
【解析】【解答】反比例函数 ,当 时,图像分布在第一、三象限;当 时,图像分布在第二、四象限;所以选B;
【分析】此题考查反比例函数图象的性质;
5.【答案】D
【解析】【解答】解:A. 如果两个角相等,那么这两个角不一定是对顶角,不符合题意;
B. 经过直线外一点有且只有一条直线与已知直线平行,不符合题意;
C. 如果两条平行线被第三条直线所截,那么内错角相等,不符合题意;
D. 联结直线外一点与直线上各点的所有线段中,垂线段最短,符合题意;
故答案为:D.
【分析】根据对顶角的定义,平行线爱你的定义,平行公理和垂线的性质分别进行判断,即可求出答案。
6.【答案】D
【解析】【解答】解:∵x+y=6,xy=4,
∴x2y+xy2=xy(x+y)=4×6=24.
故选:D.
【分析】直接利用提取公因式法分解因式进而求出答案.
7.【答案】D
【解析】【解答】解:∵四边形ABCD是菱形,∠BAD=120°,
∴∠B=∠DAC=∠BAC=∠BCA=60°,AB=BC=AC,
∵BE=AF,
∴△BCE≌△ACF(SAS),故①正确;
∴CF=CE,∠BCE=∠ACF,
∵∠ACF=∠ACF+∠ACE=∠BCE+∠ACE=∠BCA=60°,
∴△CEF为正三角形.故②正确;
∵∠AGE=∠GAF+∠AFG=60°+∠AFG=∠AFC,
∴AGE=∠BEC 故③正确;
∵AF=1,∴BE=1,
∴AE=4-1=3
过点E作EH∥BC交AC于点H.
∴,即 ,∴EH=3,
∵AF∥EH,
∴,即得EG=3FG ,故④正确.
故答案为:D.
【分析】根据菱形的性质,可得∠B=∠FAC=60°,BC=AC,根据“SAS”可证△BCE≌△ACF,据此判断①;利用全等三角形的对应边相等,对应角相等,可得CF=CE,∠BCE=∠ACF,从而可得∠ECF=∠BCA=60°,即证△CEF为正三角形,据此判断②;由∠AGE=∠GAF+∠AFG=60°,+∠AFG=∠AFC,据此判断③;过点E作EH∥BC交AC于点H.利用平行线分线段成比例,可求出EH=3,从而可得 ,从而可得EG=3FG ,据此判断④
8.【答案】C
【解析】【分析】根据三角函数的定义就可以解决.
【解答】设Rt△ABC的两直角边分别为a、b,斜边为c,
则sinA=,cosB= .
∴sinA=cosB.
故选C.
9.【答案】D
【解析】【解答】解:过点C作CD⊥AB于点D∠PQ于点E,
∵在Rt△BCD中,∠B=30°,BC=10
∴CD=BC=5,
设CE=x,则DE=5-x
∵PQ∥AB
∴CD⊥PQ,△PCQ∽△ABC
∴即
解之:PQ=2x
设△APQ的面积为S
∴S=PQ·DE=·2x(5-x)=
∵a=-1,抛物线的开口向下,
∴当时,S有最大值为=6.25.
故答案为:D.
【分析】过点C作CD⊥AB于点D∠PQ于点E,利用直角三角形的性质求出CD的长,设CE=x,用含x的代数式表示出DE,再证明△PCQ∽△ABC,利用相似三角形的对应边成比例求出PQ=2x,然后利用三角形的面积公式建立S与x的函数解析式,将函数解析式转化为顶点式,利用二次函数的性质可求解。
10.【答案】C
【解析】【解答】解:过点B′作B′D⊥OC
∵∠CPB=60°,CB′=OC=OA=4
∴∠B′CD=30°,B′D=2
根据勾股定理得DC=2
∴OD=4﹣2,即B′点的坐标为(2,4-2)
故选C.
【分析】过点B′作B′D⊥OC,因为∠CPB=60°,CB′=OC=OA=4,所以∠B′CD=30°,B′D=2,根据勾股定理得DC=2,故OD=4﹣2,即B′点的坐标为(2,4-2).
11.【答案】6
【解析】【解答】解:∵△OAB的面积为3,
∴k=2S△ABO=6,
∴反比例函数的表达式是y=
即k=6
故答案为:6.
【分析】根据反比例函数k的几何意义直接求解即可.
12.【答案】①③④
【解析】【解答】解:如图,过点G作MN∥AB,分别交AD、BC于点M、N,
∵四边形ABCD为矩形,
∴AB=CD=10,BC=AD=12,
由折叠可得AB=BE,且∠A=∠ABE=∠BEF=90°,
∴四边形ABEF为正方形,
∴AF=AB=10,
故①正确;
∵MN∥AB,
∴△BNG和△FMG为等腰直角三角形,且MN=AB=10,
设BN=x,则GN=AM=x,MG=MN﹣GN=10﹣x,MD=AD﹣AM=12﹣x,
又由折叠的可知DG=DC=10,
在Rt△MDG中,由勾股定理可得MD2+MG2=GD2,
即(12﹣x)2+(10﹣x)2=102,解得x=4,
∴GN=BN=4,MG=6,MD=8,
又∠DGH=∠C=∠GMD=90°,
∴∠NGH+∠MGD=∠MGD+∠MDG=90°,
∴∠NGH=∠MDG,且∠DMG=∠GNH,
∴△MGD∽△NHG,
∴ = = ,即 = = ,
∴NH=3,GH=CH=5,
∴BH=BC﹣HC=12﹣5=7,
故④正确;
又△BNG和△FMG为等腰直角三角形,且BN=4,MG=6,
∴BG=4 ,GF=6 ,
∴△BGF的周长=BG+GH+BH=4 +5+7=12+4 , = = ,
故②不正确;③正确;
综上可知正确的为①③④,
故答案为:①③④.
【分析】过G点作MN∥AB,交AD、BC于点M、N,可知四边形ABEF为正方形,可求得AF的长,可判断①,且△BNG和△FMG为等腰三角形,设BN=x,则可表示出GN、MG、MD,利用折叠的性质可得到CD=DG,在Rt△MDG中,利用勾股定理可求得x,再利用△MGD∽△NHG,可求得NH、GH和HC,则可求得BH,容易判断②③④,可得出答案.
13.【答案】
【解析】【解答】∵∠C=90°,∠ABC=30°,AC=2,
∴AB=2AC=4,∠BAC=60°,
由旋转的性质得,∠BAB′=∠BAC=60°,
∴B点通过一次旋转至B′所经过的路径长为,
故答案为:.
【分析】先求出AB=2AC=4,∠BAC=60°,再求出∠BAB′=∠BAC=60°,最后求解即可。
14.【答案】5
【解析】【解答】解:设,,则
由题意知,
∴
∴
∴
解得
∴
∴
故答案为:5.
【分析】设A(a,),F(0,m),则B(,),由题意知∠BEF=∠DOF=90°,∠BFE=∠DFO,证明△BEF∽△DOF,根据相似三角形的性质可得m=,则EF=,然后根据三角形的面积公式进行计算.
15.【答案】① .
②
③
④
.
⑤ .
⑥
【解析】【分析】①根据有理数的运算法则计算即可.②单项式的乘除运算法则计算即可.③根据多项式除单项式的运算法则记性计算即可.④根据乘法公式计算即可.⑤先除掉相同多项式,再利用完全平方公式计算即可.⑥将y-2当做整体,再利用平方差公式计算即可.
16.【答案】解:(1)设这个二次函数的关系式为y=a(x-2)2+1.
把x=3,y=2代入得a+1=2,∴a=1.
∴这个二次函数的关系式为y=(x-2)2+1.
(2)由题意知:P(n,n2-4n+5),Q(n,-4).
∴PQ=n2-4n+5-(-4)=n2-n+9=(n-)2+.
∴当n=时,PQ取得最小值为.
易证△DPQ∽△OAB,
∴,
∵一次函数y=x-4的图象与x轴交于点A,与y轴交于点B,
∴OB=4,OA=3,AB==5
∴DQ=×PQ=.
∴当n=时,DQ取得最小值,为.
【解析】【分析】(1)由于顶点为M(2,1),故设这个二次函数的关系式为y=a(x-2)2+1,又因为过点N(3,2),代入解析式即可求出a的值,从而得到解析式;
(2)用含有n 得代数式表示出P,Q坐标,求出PQ最小值,再证得△DPQ∽△OAB,根据相似三角形性质即可求得DQ的最小值.
17.【答案】(1)解:如图,即为所求
(2)解:如图,即为所求
(3)如图,即为所求
【解析】【解答】解:(3) ,
若看成是由经过一次平移得到的,则这一平移的距离等于个单位长度,
故答案为:.
【分析】(1)根据中心对称图形的性质找出点A、B、C的对应点,再连接即可;
(2)根据旋转的性质找出点A、B、C的对应点,再连接即可;
(3)利用平移的性质求解即可。
18.【答案】(1)
(2)对于上式,左边= =右边,
故规律成立.
【解析】【解答】(1)设图形中间的数字为x,则周围四个数字可依次表示为: ,
则规律表示为: ,
故答案为: ;
【分析】(1)根据中间数字为x,分别表示出题中所述的四个数字,再按照题意列式即可;(2)利用乘法公式计算所列式子,验证即可.
19.【答案】(1)证明:∵EC⊥DE,
∴∠DEC=90°,
∵∠DAB=∠CBA=90°,
∴∠ADE+∠AED=90°,∠AED+∠CEB=90°,
∴∠ADE=∠CEB,
∴△AED∽△BCE;
(2)解:∵△AED∽△BCE,
,
∵AE=EB,
∴AE2=AD BC=36,
∴AE=EB=6,
∴DE2=AD2+AE2=32+62=45,EC2=BE2+BC2=62+122=180,
.
【解析】【分析】(1)由垂直的概念可得∠DEC=90°,根据同角的余角相等可得∠ADE=∠CEB,然后利用相似三角形的判定定理进行证明;
(2)由相似三角形的性质结合AE=EB可得AE=EB=6,利用勾股定理求出DE2、EC2,然后在Rt△CDE中,应用勾股定理就可求出CD.
20.【答案】(1)解:(1)如图②所示,过点C作CM⊥DE,垂足为M,
在Rt△CDM中,CD=70mm,∠CDM=60°,
∴sin60°===,
∴CM=,
∴点C到直线DE的距离为mm.
(2)解:如图②所示,过点A作AN⊥DE,垂足为N,过点C作CP⊥AN,垂足为P,则PN=CM=,
∵∠CDM=60°,
∴∠DCM=90°-60°=30°,
又∵∠DCB=70°,
∴∠BCM=70°-30°=40°,
又∵CM∥AN,
∴∠A=∠BCM=40°,
∴∠ACP=90°-40°=50°,
∵AB=115mm,CB=35mm,
∴AC=80mm,
∴在Rt△ACP中,sin50°==≈0.8,
∴AP=64,
∴AN=AP+PN=64+ ≈124,
∴点A到直线DE的距离约为124mm.
(3)33.4°
【解析】【解答】解:(3)如图③所示,连接BD,
在Rt△BCD中,BC=35mm,CD=70mm,
∴tan∠BDC===0.5,
∵tan26.6°≈0.5,
∴∠BDC=26.6°,
∵∠CDE=60°,
∴∠BDE=∠CDE-∠CDB=60°-26.6°=33.4°,
∴CD旋转的度数为33.4°.
故答案为:33.4°.
【分析】(1)如图②所示,过点C作CM⊥DE,垂足为M,在Rt△CDM中,由正弦关系即可求点C到直线DE的距离;
(2)如图②所示,过点A作AN⊥DE,垂足为N,过点C作CP⊥AN,垂足为P,则PN=CM=,由角互余关系求得∠DCB的度数,再由角的和差关系及平行线性质可求得∠A的度数,从而得到∠ACP的度数,再由线段和差关系求出AC的长度,在Rt△ACP中,由边角关系求出AP的长度,再由线段和差关系求得AN的长度,即可解决问题;
(3)如图③所示,连接BD,由直角三角形的边角关系求出∠BDC度数,再由角的和差关系求出∠BDE的度数即可.
21.【答案】(1)解:如图示,过点作轴,交轴于点
∵一次函数的图象经过点(0,4),且的面积为6.
∴,,
∴,即点的横坐标是3,
∵点在直线上,
∴,
∴点的坐标是:(3,)
由点(0,4),(3,)得:,
解之得:,
∴直线AB的解析式是:;
(2)解:如图示,过点作且,连接,则是以AB为直角边的等腰直角三角形;
过点作且,连接,则是以AB为直角边的等腰直角三角形;
过点作轴,交轴于点,延长,
作,交延长线于点,
∴,
∴
又∵
∴
∴
∵,
∴
∴,
∴
∴点的坐标是:(6,7);
同理可证:
∴,
∴
∴点的纵坐标是:,
∴点的坐标是:(9,1);
综上所述,以AB为直角边的等腰直角三角形,符合条件的点M的坐标是:(6,7)或(9,1).
【解析】【分析】(1)过点B作BE⊥y轴,交y轴于点E,根据点A的坐标可得OA=4,结合三角形的面积公式可得BE3,即点B的横坐标是3,代入y=x-1中可得y的值,得到点B的坐标,然后利用待定系数法就可求出直线AB的解析式;
(2)过点A作M1A=AB且M1A⊥AB,连接M1B,则△M1AB是以AB为直角边的等腰直角三角形,过点B作M2B=AB且M2B⊥AB,连接M2A,则△M2AB是以AB为直角边的等腰直角三角形,过点M1作M1 G⊥y轴,交y轴于点G,延长EB,作M1F⊥EF,交EB延长线于点F,根据同角的余角相等可得∠EAB=∠GM1A,证明△AGM1≌△BEA,得到GM1=AE=6,GA=EB=3,则GO=GA+AO=7,据此可表示出点M1的坐标;同理可得点M2的坐标.
22.【答案】(1)解:∵点D(m,n),
∴点D(m,n)的特征线是x=m,y=n,y=x+n﹣m,y=﹣x+m+n
(2)解:点D有一条特征线是y=x+1,
∴n﹣m=1,
∴n=m+1
∵抛物线解析式为 ,
∴y= (x﹣m)2+m+1,
∵四边形OABC是正方形,且D点为正方形的对称轴,D(m,n),
∴B(2m,2m),
∴ (2m﹣m)2+n=2m,将n=m+1代入得到m=2,n=3;
∴D(2,3),
∴抛物线解析式为y= (x﹣2)2+3
(3)解:如图,当点A′在平行于y轴的D点的特征线时,根据题意可得,D(2,3),∴OA′=OA=4,OM=2,∴∠A′OM=60°,∴∠A′OP=∠AOP=30°,∴MN= ,∴抛物线需要向下平移的距离=3﹣ = .
如图,当点A′在平行于x轴的D点的特征线时,设A'(p,3),
则OA'=OA=4,OE=3,EA'==∴A'F=4- 设P(4,c)(c>0),在Rt△A'FP中,( 4-)2+(3-c)2=c2
∴c= ,
∴P(4, )
∴直线OP解析式为y=x,
∴N(2,),
∴抛物线需要向下平移的距离=3﹣= ,
即:抛物线向下平移 或 距离,其顶点落在OP上.
【解析】【分析】(1)根据特征线直接求出点D的特征线;
(2)由点D的一条特征线和正方形的性质求出点D的坐标,从而求出抛物线解析式;
(3)分平行于x轴和y轴两种情况,由折叠的性质计算即可.此题是二次函数综合题,主要考查了折叠的性质,正方形的性质,特征线的理解,解本题的关键是用正方形的性质求出点D的坐标.
23.【答案】(1)解:由抛物线 过点A(-3,0),B(1,0),
则
解得
∴二次函数的关系解析式
(2)解:连接PO,作PM⊥x轴于M,PN⊥y轴于N.
设点P坐标为(m,n),则 .
PM = , ,AO=3.
当 时, =2.
∴OC=2.
=
= = .
∵ =-1<0,∴当 时,函数 有最大值.
此时 = .
∴存在点 ,使△ACP的面积最大.
(3)解:存在点Q,坐标为: , .
分△BQE∽△AOC,△EBQ∽△AOC,△QEB∽△AOC三种情况讨论可得出
【解析】【分析】(1)由题意知抛物线过点A(-3,0),B(1,0),所以用待定系数法即可求解;
(2)因为三角形ACP是任意三角形,所以可做辅助线,连接PO,作PM⊥x轴于M,PN⊥y轴于N.则三角形ACP的面积=三角形APM的面积+矩形PMON的面积-三角形AOC的面积-三角形PCN的面积。于是可设点P的 横坐标为m,则纵坐标可用含m的代数式表示出来,即M(m, m + 2),
则三角形ACP的面积可用含m的代数式表示,整理可得是一个二次函数,利用二次函数的性质即可求解;
(3)根据对应顶点的不同分三种情况(△BQE∽△AOC,△EBQ∽△AOC,△QEB∽△AOC)讨论即可求解。
1 / 1
一、单选题
1.下列函数中属于二次函数的是( )
A. B.
C. D.
2.已知,则的值为( )
A. B. C. D.
3.如图1,在中,点P从点A出发向点C运动,设x表示线段的长,y表示线段的长,下列结论不正确的是( )
A. B. C. D.
4.如图是我们学过的反比例函数图象,它的函数解析式可能是( )
A. B. C. D.
5.下列说法正确的是( )
A.如果两个角相等,那么这两个角是对顶角
B.经过一点有且只有一条直线与已知直线平行
C.如果两条直线被第三条直线所截,那么内错角相等
D.联结直线外一点与直线上各点的所有线段中,垂线段最短
6.已知x+y=6,xy=4,则x2y+xy2的值为( )
A.12 B.-12 C.-24 D.24
7.已知菱形ABCD,E、F是动点,边长为4,BE=AF,∠BAD=120°,则下列结论:
①△BCE≌△ACF②△CEF为正三角形③∠AGE=∠BEC④若AF=1,则EG=3FG正确的有( )个.
A.1 B.2 C.3 D.4
8.在Rt△ABC中,∠C=90°,下列各式中正确的是( )
A.sinA=sinB B.tanA=tanB C.sinA=cosB D.cosA=cosB
9.如图,△ABC中,BC=AB=10,∠B=30°,点P、点Q分别是AC、BC上的动点,PQ∥AB,则△APQ的最大面积为( )
A.52 B.26 C.13 D.6.25
10.如图,在平面直角坐标系中,OABC是正方形,点A的坐标是(4,0),点P为边AB上一点,∠CPB=60°,沿CP折叠正方形,折叠后,点B落在平面内点B′处,则B′点的坐标为( )
A.(2,2) B.(,2-)
C.(2,4-2) D.(,4-2)
二、填空题
11.如图,点A在双曲线y=上,AB⊥y轴于B,S△ABO =3,则k=
12.如图1,有一张矩形纸片ABCD,已知AB=10,AD=12,现将纸片进行如下操作:现将纸片沿折痕BF进行折叠,使点A落在BC边上的点E处,点F在AD上(如图2);然后将纸片沿折痕DH进行第二次折叠,使点C落在第一次的折痕BF上的点G处,点H在BC上(如图3),给出四个结论:
①AF的长为10;②△BGH的周长为18;③ = ;④GH的长为5,
其中正确的结论有 .(写出所有正确结论的番号)
13.在活动课上,“雄鹰组”用含30°角的直角三角尺设计风车.如图,∠C=90°,∠ABC=30°,AC=2,将直角三角尺绕点A逆时针旋转得到△AB′C′,使点C′落在AB边上,以此方法做下去……则B点通过一次旋转至B′所经过的路径长为 .(结果保留π)
14.如图,矩形ABCD的顶点A、B分别在反比例函数与的图象上,点C、D在x轴上,AB、BD分别交y轴于点E、F,则阴影部分的面积为 .
三、解答题
15.计算:
① ;
② ;
③ ;
④ ;
⑤ ;
⑥ .
16.如图,已知二次函数y=ax2+bx+c的图象的顶点为M(2,1),且过点N(3,2).
(1)求这个二次函数的关系式;
(2)若一次函数y=x-4的图象与x轴交于点A,与y轴交于点B,P为抛物线上的一个动点,过点P作PQ∥y轴交直线AB于点Q,以PQ为直径作圆交直线AB于点D.设点P的横坐标为n,问:当n为何值时,线段DQ的长取得最小值?最小值为多少?
17.如图,在平面直角坐标系中,ABC三个顶点的坐标分别为A(1,-4),B(5,-4),C(4,-1).
(1)画出ABC关于原点O成中心对称的A1B1C1;
(2)面出ABC绕点O逆时针旋转90°所得到的A2B2C2;
(3)将ABC先向右平移2个单位长度,再向上平移6个单位长度,画出第二次平移后的A3B3C3.若A3B3C3看成是由ABC经过一次平移得到的,则这一平移的距离等于 个单位长度.
18.在日历上,我们可以发现其中某些数满足一定的规律,如图1是2021年1月份的日历,任意选择图中所示的方框,每个框四个角上的数交叉相乘后求和,再与中间的数的平方的2倍作差,例如:3×l9+5×17﹣2×112=﹣100,14×30+16×28﹣2×222=﹣100,不难发现,结果都是﹣100.
(1)如图2,设日历中所示图形中间的数字为x,请用含x的式子表示发现的规律 ;
(2)利用整式的运算对(1)中的规律加以证明.
19.如图,在四边形ABCD中,∠DAB=∠CBA=90°,点E为AB的中点,DE⊥CE.
(1)求证:△AED∽△BCE;
(2)若AD=3,BC=12,求线段DC的长.
20.图①是一种手机平板支架,由托板、支撑板和底座构成,手机放置在托板上,托板长AB=115mm,支撑板长CD=70mm,且CB=35mm,托板AB可绕点C转动,且∠CDE=60°。(参考数据:sin50°≈0.8,cos50°≈0.6,tan50°≈1.2,sin26.6°≈0.4,cos26.6°≈0.9,tan26.6°≈0.5,≈1.7)
(1)求点C到直线DE的距离(计算结果保留根号);
(2)若∠DCB=70°时,求点A到直线DE的距离(计算结果精确到个位);
(3)为了观看舒适,把(1)中∠DCB=70°调整为90°,再将CD绕点D逆时针旋转,使点B落在DE上,则CD旋转的度数为 .(直接写出结果)
21.如图,在平面直角坐标系中,一次函数的图象与y轴交于点(0,4),与直线在第四象限相交于点B,连接OB,的面积为6.
(1)求点B的坐标及直线AB的解析式;
(2)已知点M在直线AB右侧,且△MAB是以AB为直角边的等腰直角三角形.请求出符合条件的点M的坐标.
22.阅读:我们约定,在平面直角坐标系中,经过某点且平行于坐标轴或平行于两坐标轴夹角平分线的直线,叫该点的“特征线”.例如,点M(1,3)的特征线有:x=1,y=3,y=x+2,y=﹣x+4.
问题与探究:如图,在平面直角坐标系中有正方形OABC,点B在第一象限,A、C分别在x轴和y轴上,抛物线 经过B、C两点,顶点D在正方形内部.
(1)直接写出点D(m,n)所有的特征线;
(2)若点D有一条特征线是y=x+1,求此抛物线的解析式;
(3)点P是AB边上除点A外的任意一点,连接OP,将△OAP沿着OP折叠,点A落在点A′的位置,当点A′在平行于坐标轴的D点的特征线上时,满足(2)中条件的抛物线向下平移多少距离,其顶点落在OP上?
23.在平面直角坐标系中,二次函数 的图象与 轴交于A(-3,0),B(1,0)两点,与y轴交于点C.
(1)求这个二次函数的解析式;
(2)点P是直线AC上方的抛物线上一动点,是否存在点P,使△ACP的面积最大?若存在,求出点P的坐标;若不存在,说明理由;
(3)点Q是直线AC上方的抛物线上一动点,过点Q作QE垂直于 轴,垂足为E.是否存在点Q,使以点B、Q、E为顶点的三角形与△AOC相似?若存在,直接写出点Q的坐标;若不存在,说明理由;
答案解析部分
1.【答案】A
【解析】【解答】 解:A、是二次函数,A符合题意;
B:分母含有自变量,不是二次函数,B不符合题意;
C:自变量的次数是3次,不是二次函数,C不符合题意;
D:化简后自变量最高次数是1,不是二次函数,D不符合题意.
故答案为:A.
【分析】根据二次函数的定义对选项逐一进行判断即可求解.
2.【答案】C
【解析】【解答】解:∵,
∴,
∴,
故答案为:C.
【分析】由得,然后代入化简即可.
3.【答案】C
【解析】【解答】解:当点P在A处时,即当AP=0时,BP=AB.
当点P到AC边的高BH的位置时,AH=1,此时BP最小,BH=;
当AP=4时,点P对应图2末端,此时AC=4,HC=AC-AH=4-1=3,
∴BC=.
∵22+()2=42,
∴AB2+BC2=AC2,
∴∠ABC=90°,
∴tan∠BAP=.
故答案为:C.
【分析】当点P在A处时,即当AP=0时,BP=AB.,当点P到AC边的高BH的位置时,AH=1,此时BP最小,由勾股定理可得BH,当AP=4时,有AC=4,HC=AC-AH=4-1=3,由勾股定理可得BC,根据勾股定理逆定理知△ABC为直角三角形且∠ABC=90°,利用三角函数的概念可得tan∠BAP的值,据此判断.
4.【答案】B
【解析】【解答】反比例函数 ,当 时,图像分布在第一、三象限;当 时,图像分布在第二、四象限;所以选B;
【分析】此题考查反比例函数图象的性质;
5.【答案】D
【解析】【解答】解:A. 如果两个角相等,那么这两个角不一定是对顶角,不符合题意;
B. 经过直线外一点有且只有一条直线与已知直线平行,不符合题意;
C. 如果两条平行线被第三条直线所截,那么内错角相等,不符合题意;
D. 联结直线外一点与直线上各点的所有线段中,垂线段最短,符合题意;
故答案为:D.
【分析】根据对顶角的定义,平行线爱你的定义,平行公理和垂线的性质分别进行判断,即可求出答案。
6.【答案】D
【解析】【解答】解:∵x+y=6,xy=4,
∴x2y+xy2=xy(x+y)=4×6=24.
故选:D.
【分析】直接利用提取公因式法分解因式进而求出答案.
7.【答案】D
【解析】【解答】解:∵四边形ABCD是菱形,∠BAD=120°,
∴∠B=∠DAC=∠BAC=∠BCA=60°,AB=BC=AC,
∵BE=AF,
∴△BCE≌△ACF(SAS),故①正确;
∴CF=CE,∠BCE=∠ACF,
∵∠ACF=∠ACF+∠ACE=∠BCE+∠ACE=∠BCA=60°,
∴△CEF为正三角形.故②正确;
∵∠AGE=∠GAF+∠AFG=60°+∠AFG=∠AFC,
∴AGE=∠BEC 故③正确;
∵AF=1,∴BE=1,
∴AE=4-1=3
过点E作EH∥BC交AC于点H.
∴,即 ,∴EH=3,
∵AF∥EH,
∴,即得EG=3FG ,故④正确.
故答案为:D.
【分析】根据菱形的性质,可得∠B=∠FAC=60°,BC=AC,根据“SAS”可证△BCE≌△ACF,据此判断①;利用全等三角形的对应边相等,对应角相等,可得CF=CE,∠BCE=∠ACF,从而可得∠ECF=∠BCA=60°,即证△CEF为正三角形,据此判断②;由∠AGE=∠GAF+∠AFG=60°,+∠AFG=∠AFC,据此判断③;过点E作EH∥BC交AC于点H.利用平行线分线段成比例,可求出EH=3,从而可得 ,从而可得EG=3FG ,据此判断④
8.【答案】C
【解析】【分析】根据三角函数的定义就可以解决.
【解答】设Rt△ABC的两直角边分别为a、b,斜边为c,
则sinA=,cosB= .
∴sinA=cosB.
故选C.
9.【答案】D
【解析】【解答】解:过点C作CD⊥AB于点D∠PQ于点E,
∵在Rt△BCD中,∠B=30°,BC=10
∴CD=BC=5,
设CE=x,则DE=5-x
∵PQ∥AB
∴CD⊥PQ,△PCQ∽△ABC
∴即
解之:PQ=2x
设△APQ的面积为S
∴S=PQ·DE=·2x(5-x)=
∵a=-1,抛物线的开口向下,
∴当时,S有最大值为=6.25.
故答案为:D.
【分析】过点C作CD⊥AB于点D∠PQ于点E,利用直角三角形的性质求出CD的长,设CE=x,用含x的代数式表示出DE,再证明△PCQ∽△ABC,利用相似三角形的对应边成比例求出PQ=2x,然后利用三角形的面积公式建立S与x的函数解析式,将函数解析式转化为顶点式,利用二次函数的性质可求解。
10.【答案】C
【解析】【解答】解:过点B′作B′D⊥OC
∵∠CPB=60°,CB′=OC=OA=4
∴∠B′CD=30°,B′D=2
根据勾股定理得DC=2
∴OD=4﹣2,即B′点的坐标为(2,4-2)
故选C.
【分析】过点B′作B′D⊥OC,因为∠CPB=60°,CB′=OC=OA=4,所以∠B′CD=30°,B′D=2,根据勾股定理得DC=2,故OD=4﹣2,即B′点的坐标为(2,4-2).
11.【答案】6
【解析】【解答】解:∵△OAB的面积为3,
∴k=2S△ABO=6,
∴反比例函数的表达式是y=
即k=6
故答案为:6.
【分析】根据反比例函数k的几何意义直接求解即可.
12.【答案】①③④
【解析】【解答】解:如图,过点G作MN∥AB,分别交AD、BC于点M、N,
∵四边形ABCD为矩形,
∴AB=CD=10,BC=AD=12,
由折叠可得AB=BE,且∠A=∠ABE=∠BEF=90°,
∴四边形ABEF为正方形,
∴AF=AB=10,
故①正确;
∵MN∥AB,
∴△BNG和△FMG为等腰直角三角形,且MN=AB=10,
设BN=x,则GN=AM=x,MG=MN﹣GN=10﹣x,MD=AD﹣AM=12﹣x,
又由折叠的可知DG=DC=10,
在Rt△MDG中,由勾股定理可得MD2+MG2=GD2,
即(12﹣x)2+(10﹣x)2=102,解得x=4,
∴GN=BN=4,MG=6,MD=8,
又∠DGH=∠C=∠GMD=90°,
∴∠NGH+∠MGD=∠MGD+∠MDG=90°,
∴∠NGH=∠MDG,且∠DMG=∠GNH,
∴△MGD∽△NHG,
∴ = = ,即 = = ,
∴NH=3,GH=CH=5,
∴BH=BC﹣HC=12﹣5=7,
故④正确;
又△BNG和△FMG为等腰直角三角形,且BN=4,MG=6,
∴BG=4 ,GF=6 ,
∴△BGF的周长=BG+GH+BH=4 +5+7=12+4 , = = ,
故②不正确;③正确;
综上可知正确的为①③④,
故答案为:①③④.
【分析】过G点作MN∥AB,交AD、BC于点M、N,可知四边形ABEF为正方形,可求得AF的长,可判断①,且△BNG和△FMG为等腰三角形,设BN=x,则可表示出GN、MG、MD,利用折叠的性质可得到CD=DG,在Rt△MDG中,利用勾股定理可求得x,再利用△MGD∽△NHG,可求得NH、GH和HC,则可求得BH,容易判断②③④,可得出答案.
13.【答案】
【解析】【解答】∵∠C=90°,∠ABC=30°,AC=2,
∴AB=2AC=4,∠BAC=60°,
由旋转的性质得,∠BAB′=∠BAC=60°,
∴B点通过一次旋转至B′所经过的路径长为,
故答案为:.
【分析】先求出AB=2AC=4,∠BAC=60°,再求出∠BAB′=∠BAC=60°,最后求解即可。
14.【答案】5
【解析】【解答】解:设,,则
由题意知,
∴
∴
∴
解得
∴
∴
故答案为:5.
【分析】设A(a,),F(0,m),则B(,),由题意知∠BEF=∠DOF=90°,∠BFE=∠DFO,证明△BEF∽△DOF,根据相似三角形的性质可得m=,则EF=,然后根据三角形的面积公式进行计算.
15.【答案】① .
②
③
④
.
⑤ .
⑥
【解析】【分析】①根据有理数的运算法则计算即可.②单项式的乘除运算法则计算即可.③根据多项式除单项式的运算法则记性计算即可.④根据乘法公式计算即可.⑤先除掉相同多项式,再利用完全平方公式计算即可.⑥将y-2当做整体,再利用平方差公式计算即可.
16.【答案】解:(1)设这个二次函数的关系式为y=a(x-2)2+1.
把x=3,y=2代入得a+1=2,∴a=1.
∴这个二次函数的关系式为y=(x-2)2+1.
(2)由题意知:P(n,n2-4n+5),Q(n,-4).
∴PQ=n2-4n+5-(-4)=n2-n+9=(n-)2+.
∴当n=时,PQ取得最小值为.
易证△DPQ∽△OAB,
∴,
∵一次函数y=x-4的图象与x轴交于点A,与y轴交于点B,
∴OB=4,OA=3,AB==5
∴DQ=×PQ=.
∴当n=时,DQ取得最小值,为.
【解析】【分析】(1)由于顶点为M(2,1),故设这个二次函数的关系式为y=a(x-2)2+1,又因为过点N(3,2),代入解析式即可求出a的值,从而得到解析式;
(2)用含有n 得代数式表示出P,Q坐标,求出PQ最小值,再证得△DPQ∽△OAB,根据相似三角形性质即可求得DQ的最小值.
17.【答案】(1)解:如图,即为所求
(2)解:如图,即为所求
(3)如图,即为所求
【解析】【解答】解:(3) ,
若看成是由经过一次平移得到的,则这一平移的距离等于个单位长度,
故答案为:.
【分析】(1)根据中心对称图形的性质找出点A、B、C的对应点,再连接即可;
(2)根据旋转的性质找出点A、B、C的对应点,再连接即可;
(3)利用平移的性质求解即可。
18.【答案】(1)
(2)对于上式,左边= =右边,
故规律成立.
【解析】【解答】(1)设图形中间的数字为x,则周围四个数字可依次表示为: ,
则规律表示为: ,
故答案为: ;
【分析】(1)根据中间数字为x,分别表示出题中所述的四个数字,再按照题意列式即可;(2)利用乘法公式计算所列式子,验证即可.
19.【答案】(1)证明:∵EC⊥DE,
∴∠DEC=90°,
∵∠DAB=∠CBA=90°,
∴∠ADE+∠AED=90°,∠AED+∠CEB=90°,
∴∠ADE=∠CEB,
∴△AED∽△BCE;
(2)解:∵△AED∽△BCE,
,
∵AE=EB,
∴AE2=AD BC=36,
∴AE=EB=6,
∴DE2=AD2+AE2=32+62=45,EC2=BE2+BC2=62+122=180,
.
【解析】【分析】(1)由垂直的概念可得∠DEC=90°,根据同角的余角相等可得∠ADE=∠CEB,然后利用相似三角形的判定定理进行证明;
(2)由相似三角形的性质结合AE=EB可得AE=EB=6,利用勾股定理求出DE2、EC2,然后在Rt△CDE中,应用勾股定理就可求出CD.
20.【答案】(1)解:(1)如图②所示,过点C作CM⊥DE,垂足为M,
在Rt△CDM中,CD=70mm,∠CDM=60°,
∴sin60°===,
∴CM=,
∴点C到直线DE的距离为mm.
(2)解:如图②所示,过点A作AN⊥DE,垂足为N,过点C作CP⊥AN,垂足为P,则PN=CM=,
∵∠CDM=60°,
∴∠DCM=90°-60°=30°,
又∵∠DCB=70°,
∴∠BCM=70°-30°=40°,
又∵CM∥AN,
∴∠A=∠BCM=40°,
∴∠ACP=90°-40°=50°,
∵AB=115mm,CB=35mm,
∴AC=80mm,
∴在Rt△ACP中,sin50°==≈0.8,
∴AP=64,
∴AN=AP+PN=64+ ≈124,
∴点A到直线DE的距离约为124mm.
(3)33.4°
【解析】【解答】解:(3)如图③所示,连接BD,
在Rt△BCD中,BC=35mm,CD=70mm,
∴tan∠BDC===0.5,
∵tan26.6°≈0.5,
∴∠BDC=26.6°,
∵∠CDE=60°,
∴∠BDE=∠CDE-∠CDB=60°-26.6°=33.4°,
∴CD旋转的度数为33.4°.
故答案为:33.4°.
【分析】(1)如图②所示,过点C作CM⊥DE,垂足为M,在Rt△CDM中,由正弦关系即可求点C到直线DE的距离;
(2)如图②所示,过点A作AN⊥DE,垂足为N,过点C作CP⊥AN,垂足为P,则PN=CM=,由角互余关系求得∠DCB的度数,再由角的和差关系及平行线性质可求得∠A的度数,从而得到∠ACP的度数,再由线段和差关系求出AC的长度,在Rt△ACP中,由边角关系求出AP的长度,再由线段和差关系求得AN的长度,即可解决问题;
(3)如图③所示,连接BD,由直角三角形的边角关系求出∠BDC度数,再由角的和差关系求出∠BDE的度数即可.
21.【答案】(1)解:如图示,过点作轴,交轴于点
∵一次函数的图象经过点(0,4),且的面积为6.
∴,,
∴,即点的横坐标是3,
∵点在直线上,
∴,
∴点的坐标是:(3,)
由点(0,4),(3,)得:,
解之得:,
∴直线AB的解析式是:;
(2)解:如图示,过点作且,连接,则是以AB为直角边的等腰直角三角形;
过点作且,连接,则是以AB为直角边的等腰直角三角形;
过点作轴,交轴于点,延长,
作,交延长线于点,
∴,
∴
又∵
∴
∴
∵,
∴
∴,
∴
∴点的坐标是:(6,7);
同理可证:
∴,
∴
∴点的纵坐标是:,
∴点的坐标是:(9,1);
综上所述,以AB为直角边的等腰直角三角形,符合条件的点M的坐标是:(6,7)或(9,1).
【解析】【分析】(1)过点B作BE⊥y轴,交y轴于点E,根据点A的坐标可得OA=4,结合三角形的面积公式可得BE3,即点B的横坐标是3,代入y=x-1中可得y的值,得到点B的坐标,然后利用待定系数法就可求出直线AB的解析式;
(2)过点A作M1A=AB且M1A⊥AB,连接M1B,则△M1AB是以AB为直角边的等腰直角三角形,过点B作M2B=AB且M2B⊥AB,连接M2A,则△M2AB是以AB为直角边的等腰直角三角形,过点M1作M1 G⊥y轴,交y轴于点G,延长EB,作M1F⊥EF,交EB延长线于点F,根据同角的余角相等可得∠EAB=∠GM1A,证明△AGM1≌△BEA,得到GM1=AE=6,GA=EB=3,则GO=GA+AO=7,据此可表示出点M1的坐标;同理可得点M2的坐标.
22.【答案】(1)解:∵点D(m,n),
∴点D(m,n)的特征线是x=m,y=n,y=x+n﹣m,y=﹣x+m+n
(2)解:点D有一条特征线是y=x+1,
∴n﹣m=1,
∴n=m+1
∵抛物线解析式为 ,
∴y= (x﹣m)2+m+1,
∵四边形OABC是正方形,且D点为正方形的对称轴,D(m,n),
∴B(2m,2m),
∴ (2m﹣m)2+n=2m,将n=m+1代入得到m=2,n=3;
∴D(2,3),
∴抛物线解析式为y= (x﹣2)2+3
(3)解:如图,当点A′在平行于y轴的D点的特征线时,根据题意可得,D(2,3),∴OA′=OA=4,OM=2,∴∠A′OM=60°,∴∠A′OP=∠AOP=30°,∴MN= ,∴抛物线需要向下平移的距离=3﹣ = .
如图,当点A′在平行于x轴的D点的特征线时,设A'(p,3),
则OA'=OA=4,OE=3,EA'==∴A'F=4- 设P(4,c)(c>0),在Rt△A'FP中,( 4-)2+(3-c)2=c2
∴c= ,
∴P(4, )
∴直线OP解析式为y=x,
∴N(2,),
∴抛物线需要向下平移的距离=3﹣= ,
即:抛物线向下平移 或 距离,其顶点落在OP上.
【解析】【分析】(1)根据特征线直接求出点D的特征线;
(2)由点D的一条特征线和正方形的性质求出点D的坐标,从而求出抛物线解析式;
(3)分平行于x轴和y轴两种情况,由折叠的性质计算即可.此题是二次函数综合题,主要考查了折叠的性质,正方形的性质,特征线的理解,解本题的关键是用正方形的性质求出点D的坐标.
23.【答案】(1)解:由抛物线 过点A(-3,0),B(1,0),
则
解得
∴二次函数的关系解析式
(2)解:连接PO,作PM⊥x轴于M,PN⊥y轴于N.
设点P坐标为(m,n),则 .
PM = , ,AO=3.
当 时, =2.
∴OC=2.
=
= = .
∵ =-1<0,∴当 时,函数 有最大值.
此时 = .
∴存在点 ,使△ACP的面积最大.
(3)解:存在点Q,坐标为: , .
分△BQE∽△AOC,△EBQ∽△AOC,△QEB∽△AOC三种情况讨论可得出
【解析】【分析】(1)由题意知抛物线过点A(-3,0),B(1,0),所以用待定系数法即可求解;
(2)因为三角形ACP是任意三角形,所以可做辅助线,连接PO,作PM⊥x轴于M,PN⊥y轴于N.则三角形ACP的面积=三角形APM的面积+矩形PMON的面积-三角形AOC的面积-三角形PCN的面积。于是可设点P的 横坐标为m,则纵坐标可用含m的代数式表示出来,即M(m, m + 2),
则三角形ACP的面积可用含m的代数式表示,整理可得是一个二次函数,利用二次函数的性质即可求解;
(3)根据对应顶点的不同分三种情况(△BQE∽△AOC,△EBQ∽△AOC,△QEB∽△AOC)讨论即可求解。
1 / 1
