安徽省2022-2023学年沪科版八年级上学期期末数学模拟押题试卷(含解析)
文档属性
| 名称 | 安徽省2022-2023学年沪科版八年级上学期期末数学模拟押题试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 270.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-18 16:00:37 | ||
图片预览




文档简介
安徽省2022-2023学年沪科版八年级上学期期末数学模拟押题试卷
一、单选题
1.点向左平移2个单位后恰好落在轴上,则点的坐标为( )
A. B. C. D.
2.羊年话"羊","羊"字象征着美好和吉祥,下列图案都与"羊"字有关,其中是轴对称图形的个数是( )
A.1 B.2 C.3 D.4
3.若三角形的两边长分别为4和7,则该三角形的周长可能为( )
A.9 B.14 C.18 D.22
4.如图,△ABC≌△CDA,并且AB=CD,那么下列结论错误的是( )
A.∠1=∠2 B.CA=AC C.∠D=∠B D.AC=BC
5.下列命题:①相等的两个角是对顶角;②若∠1+∠2=180°,则∠1与∠2互为补角;③同旁内角互补;④垂线段最短;⑤同角或等角的余角相等;⑥经过直线外一点,有且只有一条直线与这条直线平行,其中假命题有( )
A.1个 B.2个 C.3个 D.4个
6.如图,把 纸片沿 折叠,当点 落在四边形 内部时,则 与 之间有一种数量关系始终保持不变,试着找一找这个规律你发现的规律是( )
A. B.
C. D.
7.如图,AD是△ABC的边BC上的中线,点E是AD的中点,连接BE并延长交AC于点F,则AF:FC=( )
A.1:2 B.1:3 C.1:4 D.2:5
8.将一副三角尺按如图所示的方式摆放,则 的大小为( )
A. B. C. D.
9.如图所示, 是 的边 上的中线, cm, cm,则边 的长度可能是( )
A.3cm B.5cm C.14cm D.13cm
10.等腰三角形一边为6,另一边是方程的根,则这个等腰三角形的周长为( )
A.12 B.15 C.12或15 D.不能确定
二、填空题
11.要使式子 有意义,则 的取值范围为 .
12.将直线 向上平移1个单位长度,平移后直线的解析式为 .
13.如图,△ABC中,∠C=90°,CA=CB,点M在线段AB上,∠GMB=∠A,BG⊥MG,垂足为G,MG与BC相交于点H.若MH=8cm,则BG= cm.
14.如图,在 中, , 的中垂线EF与 的平分线交于点F,连结 并延长,交 于点D,若 ,则 的度数是 .
三、解答题
15.如图,方格纸中每个小方格都是边长为1个单位的正方形,已知 的三个顶点在格点上.
(1)画出 ,使它与 关于直线a对称;
(2)求出 的面积;
(3)在直线a上画出点P,使 最小
16.如图,直线与y轴交点的纵坐标为,直线与x轴交点的横坐标为,两条直线相交于点.
(1)关于x的不等式的解集是 ;
(2)关于x的不等式的解集是 ;
(3)当x为何值时,?
(4)当x为何值时,?
17.南海地质勘探队在南沙群岛的一小岛发现很有价值的A,B两种矿石,A矿石大约565吨,B矿石大约500吨,上报公司,要一次性将两种矿石运往冶炼厂,需要不同型号的甲、乙两种货船共30艘,甲货船每艘运费1000元,乙货船每艘运费1200元.
(1)设运送这些矿石的总费用为y元,若使用甲货船x艘,请写出y和x之间的函数关系式;
(2)如果甲货船最多可装A矿石20吨和B矿石15吨,乙货船最多可装A矿石15吨和B矿石25吨,装矿石时按此要求安排甲、乙两种货船,共有几种安排方案?哪种安排方案运费最低并求出最低运费.
18.如图1,已知射线AP是∠MAN的角平分线,点B为射线AP上的一点且AB=10,过点B分别作BC⊥AM于点C,作BD⊥AN于点D,BC=6.
(1)在图1中连接CD交AB于点O.求证:AB垂直平分CD;
(2)从A,B两题中任选一题作答,我选择 题
A.将图1中的△ABC沿射线AP的方向平移得到△ABC,点A、B、C的对应点分别为A′、B′、C′.若平移后点B的对应点B′的位置如图2,连接DB′.
①请在图2中画出此时的△A′B′C′,并在图中标注相应的字母;
②若图2中的DB′∥A′C′,写出平移的距离.
B.将图1中的△ABC沿射线AP的方向平移得到△A′B′C′,点A、B、C的对应点分别为A′、B′、C′.
①在△A′B′C′平移的过程中,若点C′与点D的连线恰好经过点B,请在图3中画出此时的△A′B′C′,并在图中标注相应的字母;
②如图3,点C′与点D的连线恰好经过点B,写出此时平移的距离.
19.某电商计划购进A,B两种新型节能台灯共100盏,这两种节能台灯的进价和售价和物流成本如下表所示:
进价(元/盏) 售价(元/盏) 物流费(元/盏)
A 60 90 5
B 100 140 10
(1)设购进A型台灯x盏,销售完这100盏台灯共获利润y元,求y与x的函数表达式(利润=售价-进价-物流费).
(2)该电商售完这100盏台灯,发现这批台灯所获利润为2800元,那么购进A、B型台灯分别是多少盏?
(3)若该电商再一次购进A、B两种台灯共100盏,A型台灯的数量为(2)问中所得B型的数量,那么,这一次与上一次相比,利润是增加了还是减少了?
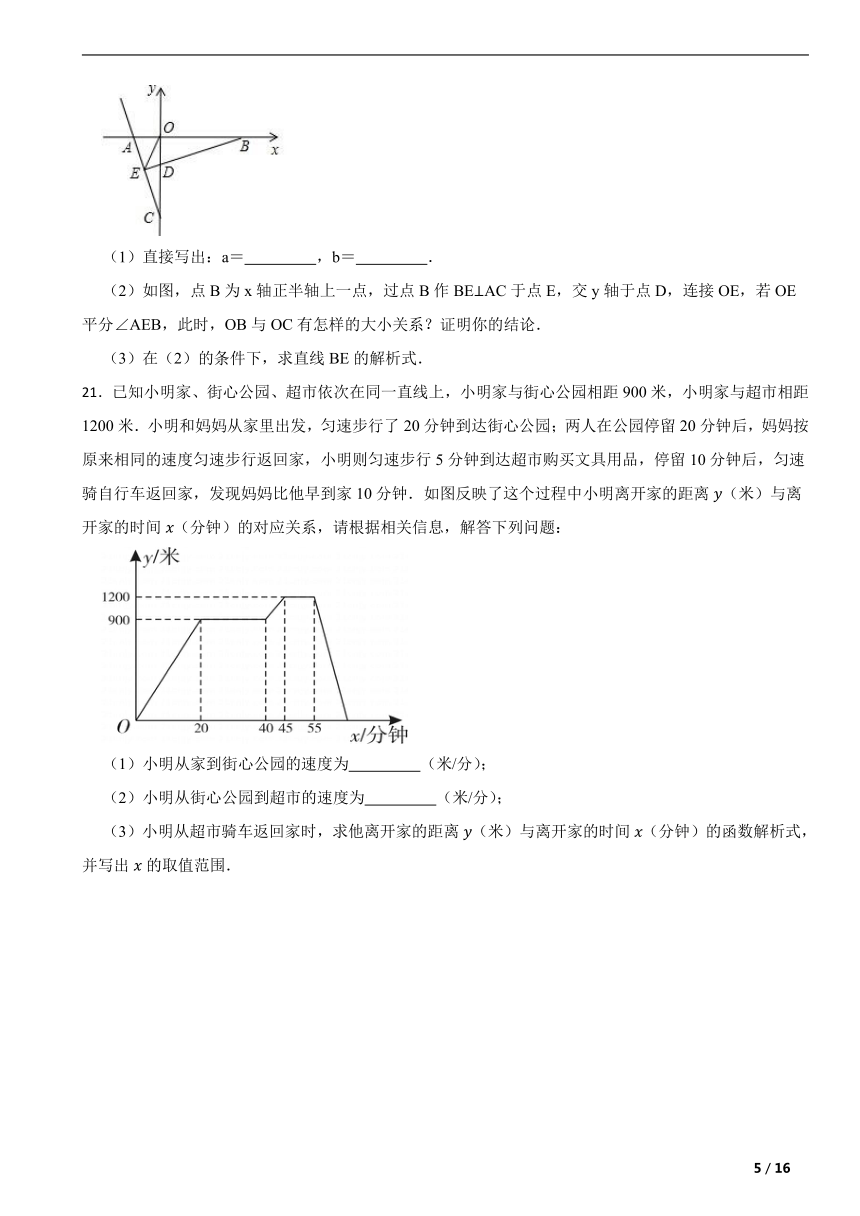
20.在平面直角坐标系中,已知点A(a,0),C(0,b),且a、b满足(a+1)2+=0.
(1)直接写出:a= ,b= .
(2)如图,点B为x轴正半轴上一点,过点B作BEAC于点E,交y轴于点D,连接OE,若OE平分∠AEB,此时,OB与OC有怎样的大小关系?证明你的结论.
(3)在(2)的条件下,求直线BE的解析式.
21.已知小明家、街心公园、超市依次在同一直线上,小明家与街心公园相距900米,小明家与超市相距1200米.小明和妈妈从家里出发,匀速步行了20分钟到达街心公园;两人在公园停留20分钟后,妈妈按原来相同的速度匀速步行返回家,小明则匀速步行5分钟到达超市购买文具用品,停留10分钟后,匀速骑自行车返回家,发现妈妈比他早到家10分钟.如图反映了这个过程中小明离开家的距离(米)与离开家的时间(分钟)的对应关系,请根据相关信息,解答下列问题:
(1)小明从家到街心公园的速度为 (米/分);
(2)小明从街心公园到超市的速度为 (米/分);
(3)小明从超市骑车返回家时,求他离开家的距离(米)与离开家的时间(分钟)的函数解析式,并写出的取值范围.
答案解析部分
1.【答案】C
【解析】【解答】解:根据题意得:m-2-2=0,
∴m=4,
∴m-2=2,m+5=9,
∴点M的坐标为:(2,9)。
故答案为:C。
【分析】根据平移与坐标的变化可得出等式m-2-2=0,从而可求出m的值,进一步求得点M的坐标即可。
2.【答案】B
【解析】【分析】根据轴对称图形的定义,即可分析出可以看成轴对称图形的汉字。
【解答】由轴对称图形的定义可得可以看成轴对称图形的汉字有“美”、“善”共2个。
故选B.
【点评】解答本题的根据是掌握好轴对称图形的定义:如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形。
3.【答案】C
【解析】【解答】解:设三角形的第三边长为x,周长为C,
∵三角形的两边长分别为4和7,
∴由三角形的三边关系可得:7-4<x<7+4,
即3<x<11,
∴三角形周长C的取值范围为14<C<22,
所以选项C符合题意,选项ABD不符合题意,
故答案为:C.
【分析】利用等腰三角形的三边关系先求出3<x<11,再求出14<C<22,最后对每个选项一一判断即可。
4.【答案】D
【解析】【解答】解:∵△ABC≌△CDA,AB=CD,
∴∠1和∠2,∠D和∠B是对应角,
∴∠1=∠2,∠D=∠B,
∴AC和CA是对应边,而不是BC,
∴A、B、C正确,D、AC=BC错误.
故答案为:D.
【分析】根据全等三角形的性质:全等三角形的对应边相等,对应角相等,逐项进行判断,即可求解.
5.【答案】B
【解析】【解答】解:相等的两个角不一定为对顶角,所以①为假命题;
若∠1+∠2=180°,则∠1与∠2互为补角,所以②为真命题;
两直线平行,同旁内角互补,所以③为假命题;
垂线段最短,所以④为真命题;
同角或等角的余角相等,所以⑤为真命题;
经过直线外一点,有且只有一条直线与这条直线平行,所以⑥为真命题.
故选B.
【分析】根据对顶角的定义对①进行判断;根据补角的定义对②进行判断;根据平行线的性质对③进行判断;根据垂线段公理对④进行判断;根据余角的定义对⑤进行判断;根据经过直线外一点,有且只有一条直线与这条直线平行可对⑥进行判断.
6.【答案】A
【解析】【解答】解:画出折叠之前的部分,如下图所示,连接
由折叠的性质可知
∵∠1是 的外角,∠2是 的外角
∴∠1= ,∠2=
∴∠1+∠2= +
=
=
=
故答案为:A.
【分析】画出折叠之前的部分,连接 ,由折叠的性质可知 ,根据三角形外角的性质可得∠1= ,∠2= ,然后将两式相加即可得出结论.
7.【答案】A
【解析】【解答】解:作DH∥AC交BF于H,如图,
∵DH∥AF,
∴∠EDH=∠EAF,∠EHD=∠EFA,
∵DE=AE,
∴△EDH≌△EAF(AAS),
∴DH=AF,
∵点D为BC的中点,DH∥CF,
∴DH为△BCF的中位线,
∴CF=2DH=2AF,
∴AF:FC=1:2,
故答案为:A.
【分析】作DH∥AC交BF于H,先利用“AAS”证明△EDH≌△EAF,可得DH=AF,再根据DH为△BCF的中位线,可得CF=2DH=2AF,再求出AF:FC=1:2即可。
8.【答案】B
【解析】【解答】解:如图所示,
由一副三角板的性质可知:∠ECD=60°,∠BCA=45°,∠D=90°,
∴∠ACD=∠ECD-∠BCA=60°-45°=15°,
∴∠α=180°-∠D-∠ACD=180°-90°-15°=75°,
故答案为:B.
【分析】先根据直角三角板的性质得出∠ACD的度数,再由三角形内角和定理即可得出结论.
9.【答案】B
【解析】【解答】解:延长AD至M使DM=AD,连接CM,
∵ 是 的边 上的中线,
∴BD=CD,
∵∠ADB=∠CDM,
∴ ,
∴MC=AB=5cm,AD=DM=4cm,
在 中,3<AC<13,
故答案为:B.
【分析】延长AD至M使DM=AD,连接CM,由中线的性质可得BD=CD,然后证明△ADB≌△MDC,得到MC=AB=5cm,AD=DM=4cm,接下来在△AMC中,应用三角形三边关系进行求解.
10.【答案】B
【解析】【解答】解:由题意知,解方程得
∴等腰三角形的一边长为6,另一边的长为3,第三边的边长为6或3
∵三角形中两边之和大于第三边,
(不合题意,舍去),
∴第三边边长为6
∴等腰三角形的周长为
故答案为:B.
【分析】先求出等腰三角形的一边长为6,另一边的长为3,第三边的边长为6或3,再求出第三边边长为6,最后求解即可。
11.【答案】x≠2020
【解析】【解答】解:由题意得,
x-2020≠0,
解得:x≠2020.
故答案为:x≠2020.
【分析】分式有意义的条件是分母不等于0,据此列式求解即可解答.
12.【答案】y=-2x+1
【解析】【解答】解:∵直线的平移规律是“上加下减”,
∴将直线 向上平移1个单位长度所得到的的直线的解析式为: ;
故答案为: .
【分析】根据直线的平移规律是上加下减的原则进行解答即可.
13.【答案】4
【解析】【解答】解:如图,过点M作MD⊥BC于D,延长DE交BG的延长线于E,
∵△ABC中,∠C=90°,CA=CB,
∴∠ABC=∠A=45°,
∵∠GMB=∠A,
∴∠GMB=∠A=22.5°,
∵BG⊥MG,
∴∠BGM=90°,
∴∠GBM=90°﹣22.5°=67.5°,
∴∠GBH=∠EBM﹣∠ABC=22.5°.
∵MD∥AC,
∴∠BMD=∠A=45°,
∴△BDM为等腰直角三角形
∴BD=DM,
而∠GBH=22.5°,
∴GM平分∠BMD,
而BG⊥MG,
∴BG=EG,即BG=BE,
∵∠MHD+∠HMD=∠E+∠HMD=90°,
∴∠MHD=∠E,
∵∠GBD=90°﹣∠E,∠HMD=90°﹣∠E,
∴∠GBD=∠HMD,
∴在△BED和△MHD中,
,
∴△BED≌△MHD(AAS),
∴BE=MH,
∴BG=MH=4.
故答案是:4.
【分析】如图,作MD⊥BC于D,延长DE交BG的延长线于E,构建等腰△BDM、全等三角形△BED和△MHD,利用等腰三角形的性质和全等三角形的对应边相等得到:BE=MH,所以BG=MH=4.
14.【答案】60°
【解析】【解答】解:∵EF垂直平分AC,∴AF=CF,
∴∠ACD=∠CAF
∵AF平分∠CAB,
∴∠CAF=∠DAF,
∵CD=CB,
∴∠CDB=∠B=3∠ACD,
又∵∠ACB+∠CAB+∠B=180°,
∴2∠ACD+3∠ACD=180°-80°,
∴∠ACD=20°,
∴∠B=60°,
故答案为:60°.
【分析】根据AF平分∠CAB得出∠CAF=∠DAF,EF垂直平分AC得出AF=CF,根据等边对等角及等量代换得出∠ACD=∠CAF=∠DAF,再由CD=CB及三角形的外角性质得出∠CDB=∠B=3∠ACD,利用三角形内角和180°,可求得∠ACB的度数,进而求出∠B的度数.
15.【答案】(1)解:如图,△A1B1C1即为所求.
(2)解: =2×2- ×1×2×2- ×1×1= .
(3)解:如图,连接C1A(或A1C)与直线a交于点P,则点P即为所求.
【解析】【分析】(1)先根据轴对称的性质找出点A、B、C关于直线a的对称点,再连接即可;
(2)利用割补法求解三角形面积即可;
(3)连接C1A(或A1C)与直线a交于点P,则点P即为所求。
16.【答案】(1)x<4
(2)x<0
(3)解:由图象可知,当x=2时,y1的图象与y2的图象交于点P(2,1.8),
当x<2时,y1的图象都在y2的图象的下方,此时y1<y2,
当x>2时,y1的图象都在y2的图象的上方,此时y1>y2,
∴当x≤2时,y1≤y2;
(4)解:由(3)得:当x>2时,y2<y1,
由(1)得:y2>0的解集为x<4,
∴当2<x<4时,0<y2<y1.
【解析】【解答】解:(1)由图象可知:令y2=0,则ax+b=0,此时x=4,
根据图象可知,直线y2=ax+b的y值随x的增大而减小,
所以,不等式ax+b>0的解集为x<4,
故答案为:x<4;
(2)由图象可知:令y1=1,则mx+n=1,此时x=0,
根据图象可知,直线y1=mx+n的y值随x的增大而增大,
所以,不等式mx+n<1的解集为x<0,
故答案为:x<0;
【分析】 (1)结合函数图象直接求解即可;
(2)结合函数图象直接求解即可;
(3)根据函数值大的图象在上方的原则求解即可;
(4)结合函数图象,再利用函数值大的图象在上方的原则求解即可。
17.【答案】(1)解:根据题意得:y=1000x+1200(30﹣x)=36000﹣200x.
(2)解:设安排甲货船x艘,则安排乙货船30﹣x艘,
根据题意得:,
化简得:,
∴23≤x≤25,
∵x为整数,
∴x=23,24,25,
方案一:甲货船23艘,则安排乙货船7艘,
运费y=36000﹣200×23=31400元;
方案二:甲货船24艘,则安排乙货船6艘,
运费y=36000﹣200×24=31200元;
方案三:甲货船25艘,则安排乙货船5艘,
运费y=36000﹣200×25=31000元;
经分析得方案三运费最低,为31000元.
【解析】【分析】(1)根据这些矿石的总费用为y=甲货船运费+乙货船运费,即可解答;
(2)根据A矿石大约565吨,B矿石大约500吨,列出不等式组,确定x的取值范围,根据x为整数,确定x的取值,即可解答.
18.【答案】(1)解:证明:如图1中,
∵BC⊥AM,BD⊥AN,
∴∠ACB=∠ADB=90°,
∵∠BAC=∠BAD,AB=AB,
∴△ABC≌△ABD,
∴AC=AD,BC=BD,
∴AB垂直平分线段CD.
(2)解:A:①△A′B′C′如图所示; ②作DH⊥AB于H. 在Rt△ABD中,AB=10,BD=BC=6, ∴AD= =8, ∵cos∠DAH= = , ∴AH= , ∵DB′∥AC, ∴∠AB′D=∠CAB, ∵∠CAB=∠DAB, ∴∠DAB=∠AB′D, ∴DA=DB′,∵DH⊥AB′, ∴AH=HB′, ∴AB′= , ∴BB′=AB′﹣AB= ﹣10= , ∴平移的距离为 , B:①△A′B′C′如图所示: ②作C′H⊥AP于H. ∵∠ABD=∠C′BB′=∠C′B′A′, ∴C′B=C′B′, ∵C′H⊥BB′, ∴BH=HB′, ∵cos∠A′B′C′= , ∴ , ∴HB′= , ∴BB′=2B′H= , ∴平移的距离为 . 故答案为A或B, , .
【解析】【分析】(1)只要证明△ABC≌△ABD,即可推出AC=AD,BC=BD,可得AB垂直平分线段CD;(2)A:①作出△A′B′C′即可;②作DH⊥AB于H.首先证明DA=DB′,想办法求出AH即可解决问题;B:①作出△A′B′C′即可;②作C′H⊥AP于H.首先证明C′B=C′B′,想办法求出B′H即可解决问题.
19.【答案】(1)解:根据题意,得购进B型台灯 盏
∴
∴ ;
(2)解:根据题意,得
将 代入到 ,得
∴ ,即购进A型台灯40盏
∴购进B型台灯 盏;
(3)解:结合(2)的结论,根据题意,得A型台灯的数量为 盏
∴购进B型台灯 盏
∴这一次利润 元
∵
∴这一次与上一次相比,利润是减少了.
【解析】【分析】(1)根据题意得购进B型台灯(100-x)盏,根据(售价-进价-物流费)×对应的盏数可得y与x的关系式;
(2)令(1)关系式中的y=2800,求出x的值,据此解答;
(3)结合(2)的结论可得A型台灯的数量为60盏,购进B型台灯40盏,然后根据(售价-进价-物流费)×对应的盏数求出利润,再与2800进行比较即可判断.
20.【答案】(1)-1;-3
(2)解:OB=OC,证明如下:如图,过O作OF⊥OE,交BE于F,
∵BE⊥AC,OE平分∠AEB,∴△EOF为等腰直角三角形,∴∠EOC+∠DOF=∠DOF+∠FOB=90°,∴∠EOC=∠FOB,且∠OEC=∠OFB=135°,在△EOC和△FOB中,,
∴△EOC≌△FOB(ASA),∴OB=OC;
(3)解:∵△EOC≌△FOB,∴∠OCE=∠OBE,OB=OC,在△AOC和△DOB中,,∴△AOC≌△DOB(ASA),∴OD=OA,∵A(-1,0),C(0,-3),∴OD=1,OC=3,∴D(0,-1),B(3,0),设直线BE解析式为y=kx+b,把B、D两点坐标代入可得,解得.∴直线BE的解析式为.
【解析】【解答】(1)解:∵(a+1)2+=0,∴a+1=0,b+3=0,∴a=-1,b=-3,故答案为:-1;-3;
【分析】(1)利用非负数之和为0的性质求出a、b的值即可;
(2)过O作OF⊥OE,交BE于F,利用“ASA”证明△EOC≌△FOB,再利用全等三角形的性质可得OB=OC;
(3)先求出点B、D的坐标,再利用待定系数法求出函数解析式即可。
21.【答案】(1)45
(2)
(3)解:由题可知,妈妈回家所用时间为 ;妈妈比小明早到家10分钟,
∴小明骑自行车返回家的时间为: ;
∴小明到家时途中所对应的坐标为; ;
设小明从超市骑车返回家时,他离开家的距离 (米)与离开家的时间 (分钟)的函数解析式为
将 、 代入 得, ;
解得: ,
∴ .
(2)
(3)
【解析】【解答】解:(1)由题意得,
故答案为:45;
(2)由题意得,
故答案为:60;
【分析】(1)根据题意即可求解;
(2)根据题意即可求解;
(3)先根据题意得到小明到家时途中所对应的坐标为:,设小明从超市骑车返回家时,他离开家的距离 (米)与离开家的时间 (分钟)的函数解析式为 ,再运用待定系数法求一次函数解析式即可求解。
1 / 1
一、单选题
1.点向左平移2个单位后恰好落在轴上,则点的坐标为( )
A. B. C. D.
2.羊年话"羊","羊"字象征着美好和吉祥,下列图案都与"羊"字有关,其中是轴对称图形的个数是( )
A.1 B.2 C.3 D.4
3.若三角形的两边长分别为4和7,则该三角形的周长可能为( )
A.9 B.14 C.18 D.22
4.如图,△ABC≌△CDA,并且AB=CD,那么下列结论错误的是( )
A.∠1=∠2 B.CA=AC C.∠D=∠B D.AC=BC
5.下列命题:①相等的两个角是对顶角;②若∠1+∠2=180°,则∠1与∠2互为补角;③同旁内角互补;④垂线段最短;⑤同角或等角的余角相等;⑥经过直线外一点,有且只有一条直线与这条直线平行,其中假命题有( )
A.1个 B.2个 C.3个 D.4个
6.如图,把 纸片沿 折叠,当点 落在四边形 内部时,则 与 之间有一种数量关系始终保持不变,试着找一找这个规律你发现的规律是( )
A. B.
C. D.
7.如图,AD是△ABC的边BC上的中线,点E是AD的中点,连接BE并延长交AC于点F,则AF:FC=( )
A.1:2 B.1:3 C.1:4 D.2:5
8.将一副三角尺按如图所示的方式摆放,则 的大小为( )
A. B. C. D.
9.如图所示, 是 的边 上的中线, cm, cm,则边 的长度可能是( )
A.3cm B.5cm C.14cm D.13cm
10.等腰三角形一边为6,另一边是方程的根,则这个等腰三角形的周长为( )
A.12 B.15 C.12或15 D.不能确定
二、填空题
11.要使式子 有意义,则 的取值范围为 .
12.将直线 向上平移1个单位长度,平移后直线的解析式为 .
13.如图,△ABC中,∠C=90°,CA=CB,点M在线段AB上,∠GMB=∠A,BG⊥MG,垂足为G,MG与BC相交于点H.若MH=8cm,则BG= cm.
14.如图,在 中, , 的中垂线EF与 的平分线交于点F,连结 并延长,交 于点D,若 ,则 的度数是 .
三、解答题
15.如图,方格纸中每个小方格都是边长为1个单位的正方形,已知 的三个顶点在格点上.
(1)画出 ,使它与 关于直线a对称;
(2)求出 的面积;
(3)在直线a上画出点P,使 最小
16.如图,直线与y轴交点的纵坐标为,直线与x轴交点的横坐标为,两条直线相交于点.
(1)关于x的不等式的解集是 ;
(2)关于x的不等式的解集是 ;
(3)当x为何值时,?
(4)当x为何值时,?
17.南海地质勘探队在南沙群岛的一小岛发现很有价值的A,B两种矿石,A矿石大约565吨,B矿石大约500吨,上报公司,要一次性将两种矿石运往冶炼厂,需要不同型号的甲、乙两种货船共30艘,甲货船每艘运费1000元,乙货船每艘运费1200元.
(1)设运送这些矿石的总费用为y元,若使用甲货船x艘,请写出y和x之间的函数关系式;
(2)如果甲货船最多可装A矿石20吨和B矿石15吨,乙货船最多可装A矿石15吨和B矿石25吨,装矿石时按此要求安排甲、乙两种货船,共有几种安排方案?哪种安排方案运费最低并求出最低运费.
18.如图1,已知射线AP是∠MAN的角平分线,点B为射线AP上的一点且AB=10,过点B分别作BC⊥AM于点C,作BD⊥AN于点D,BC=6.
(1)在图1中连接CD交AB于点O.求证:AB垂直平分CD;
(2)从A,B两题中任选一题作答,我选择 题
A.将图1中的△ABC沿射线AP的方向平移得到△ABC,点A、B、C的对应点分别为A′、B′、C′.若平移后点B的对应点B′的位置如图2,连接DB′.
①请在图2中画出此时的△A′B′C′,并在图中标注相应的字母;
②若图2中的DB′∥A′C′,写出平移的距离.
B.将图1中的△ABC沿射线AP的方向平移得到△A′B′C′,点A、B、C的对应点分别为A′、B′、C′.
①在△A′B′C′平移的过程中,若点C′与点D的连线恰好经过点B,请在图3中画出此时的△A′B′C′,并在图中标注相应的字母;
②如图3,点C′与点D的连线恰好经过点B,写出此时平移的距离.
19.某电商计划购进A,B两种新型节能台灯共100盏,这两种节能台灯的进价和售价和物流成本如下表所示:
进价(元/盏) 售价(元/盏) 物流费(元/盏)
A 60 90 5
B 100 140 10
(1)设购进A型台灯x盏,销售完这100盏台灯共获利润y元,求y与x的函数表达式(利润=售价-进价-物流费).
(2)该电商售完这100盏台灯,发现这批台灯所获利润为2800元,那么购进A、B型台灯分别是多少盏?
(3)若该电商再一次购进A、B两种台灯共100盏,A型台灯的数量为(2)问中所得B型的数量,那么,这一次与上一次相比,利润是增加了还是减少了?
20.在平面直角坐标系中,已知点A(a,0),C(0,b),且a、b满足(a+1)2+=0.
(1)直接写出:a= ,b= .
(2)如图,点B为x轴正半轴上一点,过点B作BEAC于点E,交y轴于点D,连接OE,若OE平分∠AEB,此时,OB与OC有怎样的大小关系?证明你的结论.
(3)在(2)的条件下,求直线BE的解析式.
21.已知小明家、街心公园、超市依次在同一直线上,小明家与街心公园相距900米,小明家与超市相距1200米.小明和妈妈从家里出发,匀速步行了20分钟到达街心公园;两人在公园停留20分钟后,妈妈按原来相同的速度匀速步行返回家,小明则匀速步行5分钟到达超市购买文具用品,停留10分钟后,匀速骑自行车返回家,发现妈妈比他早到家10分钟.如图反映了这个过程中小明离开家的距离(米)与离开家的时间(分钟)的对应关系,请根据相关信息,解答下列问题:
(1)小明从家到街心公园的速度为 (米/分);
(2)小明从街心公园到超市的速度为 (米/分);
(3)小明从超市骑车返回家时,求他离开家的距离(米)与离开家的时间(分钟)的函数解析式,并写出的取值范围.
答案解析部分
1.【答案】C
【解析】【解答】解:根据题意得:m-2-2=0,
∴m=4,
∴m-2=2,m+5=9,
∴点M的坐标为:(2,9)。
故答案为:C。
【分析】根据平移与坐标的变化可得出等式m-2-2=0,从而可求出m的值,进一步求得点M的坐标即可。
2.【答案】B
【解析】【分析】根据轴对称图形的定义,即可分析出可以看成轴对称图形的汉字。
【解答】由轴对称图形的定义可得可以看成轴对称图形的汉字有“美”、“善”共2个。
故选B.
【点评】解答本题的根据是掌握好轴对称图形的定义:如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形。
3.【答案】C
【解析】【解答】解:设三角形的第三边长为x,周长为C,
∵三角形的两边长分别为4和7,
∴由三角形的三边关系可得:7-4<x<7+4,
即3<x<11,
∴三角形周长C的取值范围为14<C<22,
所以选项C符合题意,选项ABD不符合题意,
故答案为:C.
【分析】利用等腰三角形的三边关系先求出3<x<11,再求出14<C<22,最后对每个选项一一判断即可。
4.【答案】D
【解析】【解答】解:∵△ABC≌△CDA,AB=CD,
∴∠1和∠2,∠D和∠B是对应角,
∴∠1=∠2,∠D=∠B,
∴AC和CA是对应边,而不是BC,
∴A、B、C正确,D、AC=BC错误.
故答案为:D.
【分析】根据全等三角形的性质:全等三角形的对应边相等,对应角相等,逐项进行判断,即可求解.
5.【答案】B
【解析】【解答】解:相等的两个角不一定为对顶角,所以①为假命题;
若∠1+∠2=180°,则∠1与∠2互为补角,所以②为真命题;
两直线平行,同旁内角互补,所以③为假命题;
垂线段最短,所以④为真命题;
同角或等角的余角相等,所以⑤为真命题;
经过直线外一点,有且只有一条直线与这条直线平行,所以⑥为真命题.
故选B.
【分析】根据对顶角的定义对①进行判断;根据补角的定义对②进行判断;根据平行线的性质对③进行判断;根据垂线段公理对④进行判断;根据余角的定义对⑤进行判断;根据经过直线外一点,有且只有一条直线与这条直线平行可对⑥进行判断.
6.【答案】A
【解析】【解答】解:画出折叠之前的部分,如下图所示,连接
由折叠的性质可知
∵∠1是 的外角,∠2是 的外角
∴∠1= ,∠2=
∴∠1+∠2= +
=
=
=
故答案为:A.
【分析】画出折叠之前的部分,连接 ,由折叠的性质可知 ,根据三角形外角的性质可得∠1= ,∠2= ,然后将两式相加即可得出结论.
7.【答案】A
【解析】【解答】解:作DH∥AC交BF于H,如图,
∵DH∥AF,
∴∠EDH=∠EAF,∠EHD=∠EFA,
∵DE=AE,
∴△EDH≌△EAF(AAS),
∴DH=AF,
∵点D为BC的中点,DH∥CF,
∴DH为△BCF的中位线,
∴CF=2DH=2AF,
∴AF:FC=1:2,
故答案为:A.
【分析】作DH∥AC交BF于H,先利用“AAS”证明△EDH≌△EAF,可得DH=AF,再根据DH为△BCF的中位线,可得CF=2DH=2AF,再求出AF:FC=1:2即可。
8.【答案】B
【解析】【解答】解:如图所示,
由一副三角板的性质可知:∠ECD=60°,∠BCA=45°,∠D=90°,
∴∠ACD=∠ECD-∠BCA=60°-45°=15°,
∴∠α=180°-∠D-∠ACD=180°-90°-15°=75°,
故答案为:B.
【分析】先根据直角三角板的性质得出∠ACD的度数,再由三角形内角和定理即可得出结论.
9.【答案】B
【解析】【解答】解:延长AD至M使DM=AD,连接CM,
∵ 是 的边 上的中线,
∴BD=CD,
∵∠ADB=∠CDM,
∴ ,
∴MC=AB=5cm,AD=DM=4cm,
在 中,3<AC<13,
故答案为:B.
【分析】延长AD至M使DM=AD,连接CM,由中线的性质可得BD=CD,然后证明△ADB≌△MDC,得到MC=AB=5cm,AD=DM=4cm,接下来在△AMC中,应用三角形三边关系进行求解.
10.【答案】B
【解析】【解答】解:由题意知,解方程得
∴等腰三角形的一边长为6,另一边的长为3,第三边的边长为6或3
∵三角形中两边之和大于第三边,
(不合题意,舍去),
∴第三边边长为6
∴等腰三角形的周长为
故答案为:B.
【分析】先求出等腰三角形的一边长为6,另一边的长为3,第三边的边长为6或3,再求出第三边边长为6,最后求解即可。
11.【答案】x≠2020
【解析】【解答】解:由题意得,
x-2020≠0,
解得:x≠2020.
故答案为:x≠2020.
【分析】分式有意义的条件是分母不等于0,据此列式求解即可解答.
12.【答案】y=-2x+1
【解析】【解答】解:∵直线的平移规律是“上加下减”,
∴将直线 向上平移1个单位长度所得到的的直线的解析式为: ;
故答案为: .
【分析】根据直线的平移规律是上加下减的原则进行解答即可.
13.【答案】4
【解析】【解答】解:如图,过点M作MD⊥BC于D,延长DE交BG的延长线于E,
∵△ABC中,∠C=90°,CA=CB,
∴∠ABC=∠A=45°,
∵∠GMB=∠A,
∴∠GMB=∠A=22.5°,
∵BG⊥MG,
∴∠BGM=90°,
∴∠GBM=90°﹣22.5°=67.5°,
∴∠GBH=∠EBM﹣∠ABC=22.5°.
∵MD∥AC,
∴∠BMD=∠A=45°,
∴△BDM为等腰直角三角形
∴BD=DM,
而∠GBH=22.5°,
∴GM平分∠BMD,
而BG⊥MG,
∴BG=EG,即BG=BE,
∵∠MHD+∠HMD=∠E+∠HMD=90°,
∴∠MHD=∠E,
∵∠GBD=90°﹣∠E,∠HMD=90°﹣∠E,
∴∠GBD=∠HMD,
∴在△BED和△MHD中,
,
∴△BED≌△MHD(AAS),
∴BE=MH,
∴BG=MH=4.
故答案是:4.
【分析】如图,作MD⊥BC于D,延长DE交BG的延长线于E,构建等腰△BDM、全等三角形△BED和△MHD,利用等腰三角形的性质和全等三角形的对应边相等得到:BE=MH,所以BG=MH=4.
14.【答案】60°
【解析】【解答】解:∵EF垂直平分AC,∴AF=CF,
∴∠ACD=∠CAF
∵AF平分∠CAB,
∴∠CAF=∠DAF,
∵CD=CB,
∴∠CDB=∠B=3∠ACD,
又∵∠ACB+∠CAB+∠B=180°,
∴2∠ACD+3∠ACD=180°-80°,
∴∠ACD=20°,
∴∠B=60°,
故答案为:60°.
【分析】根据AF平分∠CAB得出∠CAF=∠DAF,EF垂直平分AC得出AF=CF,根据等边对等角及等量代换得出∠ACD=∠CAF=∠DAF,再由CD=CB及三角形的外角性质得出∠CDB=∠B=3∠ACD,利用三角形内角和180°,可求得∠ACB的度数,进而求出∠B的度数.
15.【答案】(1)解:如图,△A1B1C1即为所求.
(2)解: =2×2- ×1×2×2- ×1×1= .
(3)解:如图,连接C1A(或A1C)与直线a交于点P,则点P即为所求.
【解析】【分析】(1)先根据轴对称的性质找出点A、B、C关于直线a的对称点,再连接即可;
(2)利用割补法求解三角形面积即可;
(3)连接C1A(或A1C)与直线a交于点P,则点P即为所求。
16.【答案】(1)x<4
(2)x<0
(3)解:由图象可知,当x=2时,y1的图象与y2的图象交于点P(2,1.8),
当x<2时,y1的图象都在y2的图象的下方,此时y1<y2,
当x>2时,y1的图象都在y2的图象的上方,此时y1>y2,
∴当x≤2时,y1≤y2;
(4)解:由(3)得:当x>2时,y2<y1,
由(1)得:y2>0的解集为x<4,
∴当2<x<4时,0<y2<y1.
【解析】【解答】解:(1)由图象可知:令y2=0,则ax+b=0,此时x=4,
根据图象可知,直线y2=ax+b的y值随x的增大而减小,
所以,不等式ax+b>0的解集为x<4,
故答案为:x<4;
(2)由图象可知:令y1=1,则mx+n=1,此时x=0,
根据图象可知,直线y1=mx+n的y值随x的增大而增大,
所以,不等式mx+n<1的解集为x<0,
故答案为:x<0;
【分析】 (1)结合函数图象直接求解即可;
(2)结合函数图象直接求解即可;
(3)根据函数值大的图象在上方的原则求解即可;
(4)结合函数图象,再利用函数值大的图象在上方的原则求解即可。
17.【答案】(1)解:根据题意得:y=1000x+1200(30﹣x)=36000﹣200x.
(2)解:设安排甲货船x艘,则安排乙货船30﹣x艘,
根据题意得:,
化简得:,
∴23≤x≤25,
∵x为整数,
∴x=23,24,25,
方案一:甲货船23艘,则安排乙货船7艘,
运费y=36000﹣200×23=31400元;
方案二:甲货船24艘,则安排乙货船6艘,
运费y=36000﹣200×24=31200元;
方案三:甲货船25艘,则安排乙货船5艘,
运费y=36000﹣200×25=31000元;
经分析得方案三运费最低,为31000元.
【解析】【分析】(1)根据这些矿石的总费用为y=甲货船运费+乙货船运费,即可解答;
(2)根据A矿石大约565吨,B矿石大约500吨,列出不等式组,确定x的取值范围,根据x为整数,确定x的取值,即可解答.
18.【答案】(1)解:证明:如图1中,
∵BC⊥AM,BD⊥AN,
∴∠ACB=∠ADB=90°,
∵∠BAC=∠BAD,AB=AB,
∴△ABC≌△ABD,
∴AC=AD,BC=BD,
∴AB垂直平分线段CD.
(2)解:A:①△A′B′C′如图所示; ②作DH⊥AB于H. 在Rt△ABD中,AB=10,BD=BC=6, ∴AD= =8, ∵cos∠DAH= = , ∴AH= , ∵DB′∥AC, ∴∠AB′D=∠CAB, ∵∠CAB=∠DAB, ∴∠DAB=∠AB′D, ∴DA=DB′,∵DH⊥AB′, ∴AH=HB′, ∴AB′= , ∴BB′=AB′﹣AB= ﹣10= , ∴平移的距离为 , B:①△A′B′C′如图所示: ②作C′H⊥AP于H. ∵∠ABD=∠C′BB′=∠C′B′A′, ∴C′B=C′B′, ∵C′H⊥BB′, ∴BH=HB′, ∵cos∠A′B′C′= , ∴ , ∴HB′= , ∴BB′=2B′H= , ∴平移的距离为 . 故答案为A或B, , .
【解析】【分析】(1)只要证明△ABC≌△ABD,即可推出AC=AD,BC=BD,可得AB垂直平分线段CD;(2)A:①作出△A′B′C′即可;②作DH⊥AB于H.首先证明DA=DB′,想办法求出AH即可解决问题;B:①作出△A′B′C′即可;②作C′H⊥AP于H.首先证明C′B=C′B′,想办法求出B′H即可解决问题.
19.【答案】(1)解:根据题意,得购进B型台灯 盏
∴
∴ ;
(2)解:根据题意,得
将 代入到 ,得
∴ ,即购进A型台灯40盏
∴购进B型台灯 盏;
(3)解:结合(2)的结论,根据题意,得A型台灯的数量为 盏
∴购进B型台灯 盏
∴这一次利润 元
∵
∴这一次与上一次相比,利润是减少了.
【解析】【分析】(1)根据题意得购进B型台灯(100-x)盏,根据(售价-进价-物流费)×对应的盏数可得y与x的关系式;
(2)令(1)关系式中的y=2800,求出x的值,据此解答;
(3)结合(2)的结论可得A型台灯的数量为60盏,购进B型台灯40盏,然后根据(售价-进价-物流费)×对应的盏数求出利润,再与2800进行比较即可判断.
20.【答案】(1)-1;-3
(2)解:OB=OC,证明如下:如图,过O作OF⊥OE,交BE于F,
∵BE⊥AC,OE平分∠AEB,∴△EOF为等腰直角三角形,∴∠EOC+∠DOF=∠DOF+∠FOB=90°,∴∠EOC=∠FOB,且∠OEC=∠OFB=135°,在△EOC和△FOB中,,
∴△EOC≌△FOB(ASA),∴OB=OC;
(3)解:∵△EOC≌△FOB,∴∠OCE=∠OBE,OB=OC,在△AOC和△DOB中,,∴△AOC≌△DOB(ASA),∴OD=OA,∵A(-1,0),C(0,-3),∴OD=1,OC=3,∴D(0,-1),B(3,0),设直线BE解析式为y=kx+b,把B、D两点坐标代入可得,解得.∴直线BE的解析式为.
【解析】【解答】(1)解:∵(a+1)2+=0,∴a+1=0,b+3=0,∴a=-1,b=-3,故答案为:-1;-3;
【分析】(1)利用非负数之和为0的性质求出a、b的值即可;
(2)过O作OF⊥OE,交BE于F,利用“ASA”证明△EOC≌△FOB,再利用全等三角形的性质可得OB=OC;
(3)先求出点B、D的坐标,再利用待定系数法求出函数解析式即可。
21.【答案】(1)45
(2)
(3)解:由题可知,妈妈回家所用时间为 ;妈妈比小明早到家10分钟,
∴小明骑自行车返回家的时间为: ;
∴小明到家时途中所对应的坐标为; ;
设小明从超市骑车返回家时,他离开家的距离 (米)与离开家的时间 (分钟)的函数解析式为
将 、 代入 得, ;
解得: ,
∴ .
(2)
(3)
【解析】【解答】解:(1)由题意得,
故答案为:45;
(2)由题意得,
故答案为:60;
【分析】(1)根据题意即可求解;
(2)根据题意即可求解;
(3)先根据题意得到小明到家时途中所对应的坐标为:,设小明从超市骑车返回家时,他离开家的距离 (米)与离开家的时间 (分钟)的函数解析式为 ,再运用待定系数法求一次函数解析式即可求解。
1 / 1
同课章节目录
