4.3《角》课件(共23张PPT)2023-2024学年北师大版数学七年级上册
文档属性
| 名称 | 4.3《角》课件(共23张PPT)2023-2024学年北师大版数学七年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-18 00:00:00 | ||
图片预览







文档简介
(共23张PPT)
3 角
配套北师大版
1.通过丰富的实例,进一步理解角的有关概念和角的表示方法.
2.能在具体情境中进行角的表示,进一步认识平角、周角.
3.认识角的常用度量单位:度、分、秒,并会进行简单的计算.
4.能够应用所学知识解决实际问题,培养应用意识.
学习目标
重点
难点
准备好了吗?一起去探索吧!
角
你能在图中找到角吗?
情境导入
你能说一说这些角的共同特征吗?
都有两条边和一个顶点.
你能在图中找到角吗?
情境导入
说一说生活中的角!
生活中的角.
情境导入
这节课我们在此基础上进一步探究角.
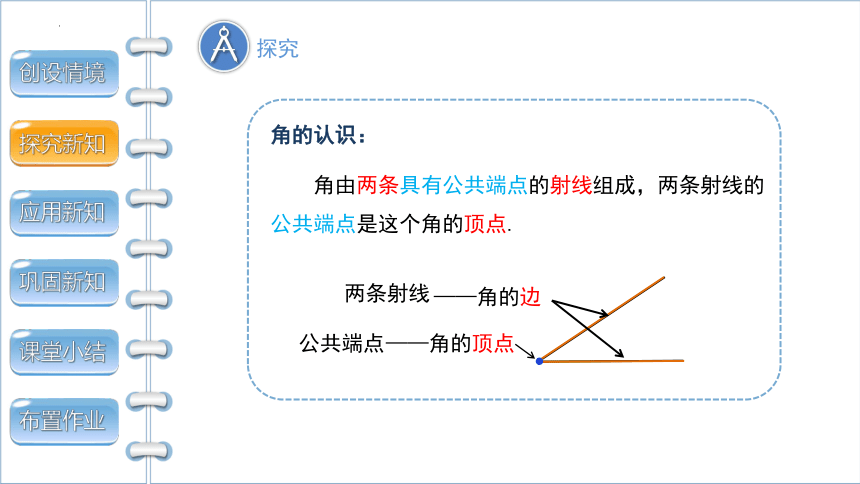
角的认识:
角由两条具有公共端点的射线组成,两条射线的公共端点是这个角的顶点.
公共端点
——角的顶点
两条射线
——角的边
探究
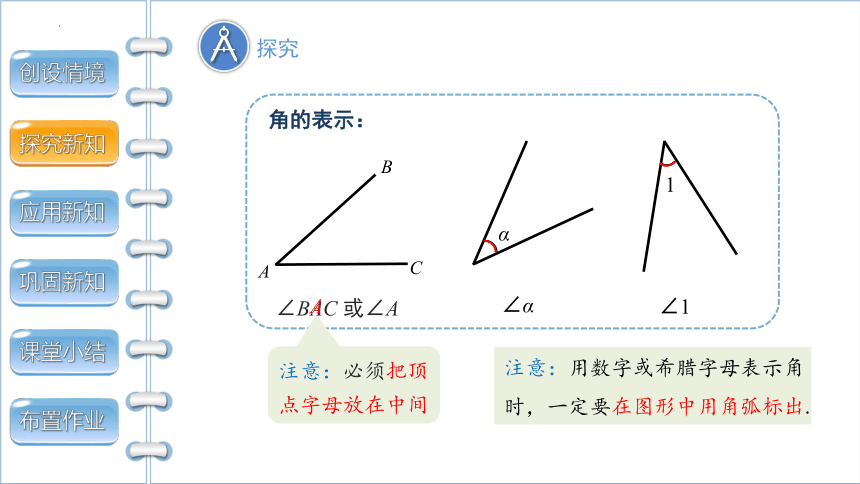
角的表示:
∠BAC 或∠A
B
C
A
α
1
∠α
∠1
注意:用数字或希腊字母表示角时,一定要在图形中用角弧标出.
注意:必须把顶点字母放在中间
A
探究
做一做
(1)用适当的方式分别表示图中的每个角.
∠BAC ,∠BAD ,∠CAD.
(2)图中,∠BAC,∠CAD和∠BAD能用∠A来表示吗?
不能
当两个或两个以上的角共用一个顶点时,不能用一个大写字母表示.
B
D
A
C
议一议
裁纸刀在开合过程中形成了大小不同的角.
你还能举出其他类似的例子吗?
用剪指甲刀剪指甲时,也可以形成大小不同的角.
归纳
角也可以看成是由一条射线绕着它的端点旋转而成的.
始边
终边
O
A
B
如果射线OB继续旋转,还会形成什么角呢?
归纳
一条射线绕它的端点旋转,当终边和始边成一条直线时,所成的角叫做平角.
O
A
B
O
A
(B)
当终边又和始边重合时,所成的角叫做周角.
延伸
为了更精密地度量角,我们规定:
1平角=180°;1周角=360°.
回顾
1°的为1分,记作1′,即1°=60′.
1′ 的为1秒,记作1″,即1′=60″.
练习
计算
(1)1.45°等于多少分?等于多少秒?
(2)1800″ 等于多少分?等于多少度?
解:(1)60′×1.45=87′,
即1.45°=87′=5220″;
(2)()′ ×1800=30′ ,
60″×87=5220″,
()°×30 =0.5°,
即1800″=30′=0.5°.
做一做
如图,是中国地图的简图.
(1)分别表示以北京为中心的每两个城市之间的夹角.
(2)哈尔滨在北京的北偏东大约多少度?
通常以正南或正北为基准,配以偏东或偏西来描述方向.
借助量角器来量一下吧!
典型例题
例1
分析
(1)0.25°等于多少分?等于多少秒?
(2)2700″ 等于多少分?等于多少度?
根据1°=60′,1′=60″来计算.
解:(1)60′×0.25=15′,
即 0.25°=15′=900″;
(2)()′ ×2700=45′,
60″×15=900″,
()°×45=0.75°,
即2700″=45′=0.75°.
每小时时针旋转的角度是360°÷12=30°;
10分钟,时针旋转的角度为5°,
10 :10时,时针与分针所夹角度为4×30°-5°=115°.
如图,时钟显示为10 :10时,时针与分针所夹角度是( )
A.90° B.100°
C.105° D.115°
典型例题
例2
分析
D
随堂练习
1.将图中的角用不同方法表示出来,并填写下表.
∠1
∠3
∠4
∠ABC
∠ACB
∠BCE
∠5
∠BAC
∠BAD
∠2
2
1
3
4
5
B
A
D
C
E
随堂练习
5°= ′= ″;38.15°= ° ′;36″= ′= °;
38°15′= °.
300
18000
38
9
0.6
0.01
38.25
2.填空.
3.一个公园的示意图如图所示.
(1)海洋世界在大门的正东方向,你能说出它在大门的北偏东多少度吗?
(2)虎豹园、猴山、大象馆分别在大门的北偏东(或南偏东)多少度?
随堂练习
海洋世界在大门的北偏东90°.
虎豹园在大门的南偏东0°(正南方向);
猴山在大门的北偏东0°(正北方向);
大象馆在大门的北偏东50°.
3.一个公园的示意图如图所示.
(3)在图中连接各个景点与大门,并用适当的方式表示各角.
(4)指出图中的锐角、钝角、直角、平角.
随堂练习
∠BOD,∠BOA,∠BOC,∠DOA,∠DOC,∠AOC.
∠BOD,∠DOA是锐角;
∠DOC是钝角;
∠BOA,∠AOC是直角;
∠BOC是平角.
角的定义:
角的表示方法:
角
角的度量:
单位:度、分、秒.
角由两条具有公共端点的射线组成.
角也可以看成是由一条射线绕着它的端点旋转而成的.
1°=60′,1′=60″ .
∠BAC 或∠A
B
C
A
α
1
∠α
∠1
教科书第117页
习题4.3
第2、3题
再见
3 角
配套北师大版
1.通过丰富的实例,进一步理解角的有关概念和角的表示方法.
2.能在具体情境中进行角的表示,进一步认识平角、周角.
3.认识角的常用度量单位:度、分、秒,并会进行简单的计算.
4.能够应用所学知识解决实际问题,培养应用意识.
学习目标
重点
难点
准备好了吗?一起去探索吧!
角
你能在图中找到角吗?
情境导入
你能说一说这些角的共同特征吗?
都有两条边和一个顶点.
你能在图中找到角吗?
情境导入
说一说生活中的角!
生活中的角.
情境导入
这节课我们在此基础上进一步探究角.
角的认识:
角由两条具有公共端点的射线组成,两条射线的公共端点是这个角的顶点.
公共端点
——角的顶点
两条射线
——角的边
探究
角的表示:
∠BAC 或∠A
B
C
A
α
1
∠α
∠1
注意:用数字或希腊字母表示角时,一定要在图形中用角弧标出.
注意:必须把顶点字母放在中间
A
探究
做一做
(1)用适当的方式分别表示图中的每个角.
∠BAC ,∠BAD ,∠CAD.
(2)图中,∠BAC,∠CAD和∠BAD能用∠A来表示吗?
不能
当两个或两个以上的角共用一个顶点时,不能用一个大写字母表示.
B
D
A
C
议一议
裁纸刀在开合过程中形成了大小不同的角.
你还能举出其他类似的例子吗?
用剪指甲刀剪指甲时,也可以形成大小不同的角.
归纳
角也可以看成是由一条射线绕着它的端点旋转而成的.
始边
终边
O
A
B
如果射线OB继续旋转,还会形成什么角呢?
归纳
一条射线绕它的端点旋转,当终边和始边成一条直线时,所成的角叫做平角.
O
A
B
O
A
(B)
当终边又和始边重合时,所成的角叫做周角.
延伸
为了更精密地度量角,我们规定:
1平角=180°;1周角=360°.
回顾
1°的为1分,记作1′,即1°=60′.
1′ 的为1秒,记作1″,即1′=60″.
练习
计算
(1)1.45°等于多少分?等于多少秒?
(2)1800″ 等于多少分?等于多少度?
解:(1)60′×1.45=87′,
即1.45°=87′=5220″;
(2)()′ ×1800=30′ ,
60″×87=5220″,
()°×30 =0.5°,
即1800″=30′=0.5°.
做一做
如图,是中国地图的简图.
(1)分别表示以北京为中心的每两个城市之间的夹角.
(2)哈尔滨在北京的北偏东大约多少度?
通常以正南或正北为基准,配以偏东或偏西来描述方向.
借助量角器来量一下吧!
典型例题
例1
分析
(1)0.25°等于多少分?等于多少秒?
(2)2700″ 等于多少分?等于多少度?
根据1°=60′,1′=60″来计算.
解:(1)60′×0.25=15′,
即 0.25°=15′=900″;
(2)()′ ×2700=45′,
60″×15=900″,
()°×45=0.75°,
即2700″=45′=0.75°.
每小时时针旋转的角度是360°÷12=30°;
10分钟,时针旋转的角度为5°,
10 :10时,时针与分针所夹角度为4×30°-5°=115°.
如图,时钟显示为10 :10时,时针与分针所夹角度是( )
A.90° B.100°
C.105° D.115°
典型例题
例2
分析
D
随堂练习
1.将图中的角用不同方法表示出来,并填写下表.
∠1
∠3
∠4
∠ABC
∠ACB
∠BCE
∠5
∠BAC
∠BAD
∠2
2
1
3
4
5
B
A
D
C
E
随堂练习
5°= ′= ″;38.15°= ° ′;36″= ′= °;
38°15′= °.
300
18000
38
9
0.6
0.01
38.25
2.填空.
3.一个公园的示意图如图所示.
(1)海洋世界在大门的正东方向,你能说出它在大门的北偏东多少度吗?
(2)虎豹园、猴山、大象馆分别在大门的北偏东(或南偏东)多少度?
随堂练习
海洋世界在大门的北偏东90°.
虎豹园在大门的南偏东0°(正南方向);
猴山在大门的北偏东0°(正北方向);
大象馆在大门的北偏东50°.
3.一个公园的示意图如图所示.
(3)在图中连接各个景点与大门,并用适当的方式表示各角.
(4)指出图中的锐角、钝角、直角、平角.
随堂练习
∠BOD,∠BOA,∠BOC,∠DOA,∠DOC,∠AOC.
∠BOD,∠DOA是锐角;
∠DOC是钝角;
∠BOA,∠AOC是直角;
∠BOC是平角.
角的定义:
角的表示方法:
角
角的度量:
单位:度、分、秒.
角由两条具有公共端点的射线组成.
角也可以看成是由一条射线绕着它的端点旋转而成的.
1°=60′,1′=60″ .
∠BAC 或∠A
B
C
A
α
1
∠α
∠1
教科书第117页
习题4.3
第2、3题
再见
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
