4.5《多边形和圆的初步认识》 教学课件(共24张PPT) 2023-2024学年北师大版数学七年级上册
文档属性
| 名称 | 4.5《多边形和圆的初步认识》 教学课件(共24张PPT) 2023-2024学年北师大版数学七年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-18 00:00:00 | ||
图片预览






文档简介
(共24张PPT)
5 多边形和圆的初步认识
配套北师大版
1.经历从现实世界中抽象出平面图形的过程,感受图形世界的丰富多彩.
2.在具体情境中认识多边形、正多边形、圆、扇形.
3.能根据扇形和圆的关系求扇形的圆心角的度数.
4.在丰富的活动中发展学生有条理的思考和表达能力.
学习目标
重点
难点
准备好了吗?一起去探索吧!
多边形和圆的初步认识
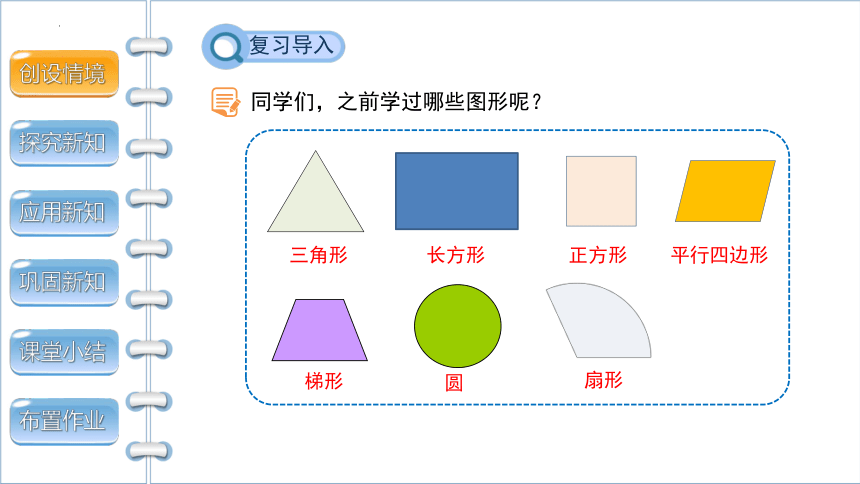
同学们,之前学过哪些图形呢?
复习导入
三角形
长方形
正方形
平行四边形
梯形
圆
扇形
图片中哪些是你熟悉的平面图形呢?
情境导入
有三角形、四边形……
有些图形不只有四条边,它们又是什么图形呢?
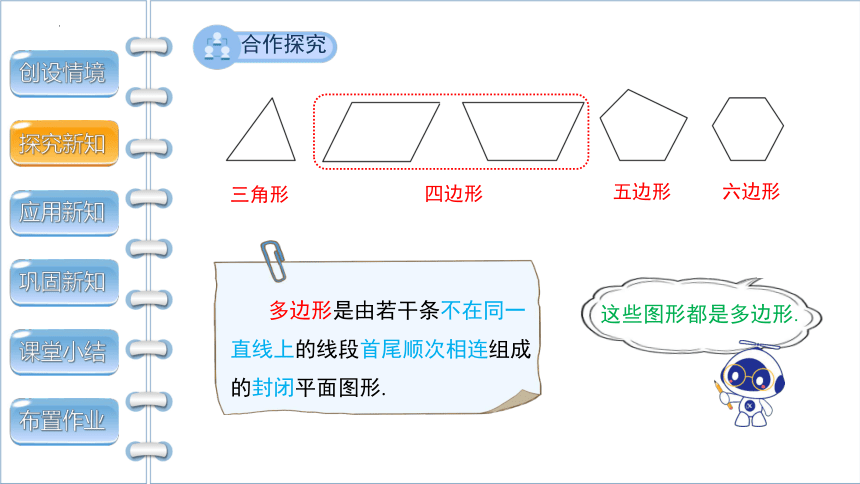
三角形
四边形
五边形
六边形
这些图形都是多边形.
多边形是由若干条不在同一直线上的线段首尾顺次相连组成的封闭平面图形.
合作探究
如图,在多边形ABCDE中,
点A,B,C,D,E是多边形的顶点;
线段AB,BC,CD,DE,EA是多边形的边;
∠EAB,∠ABC,∠BCD,∠CDE, ∠DEA是多边形的内角.
合作探究
思考
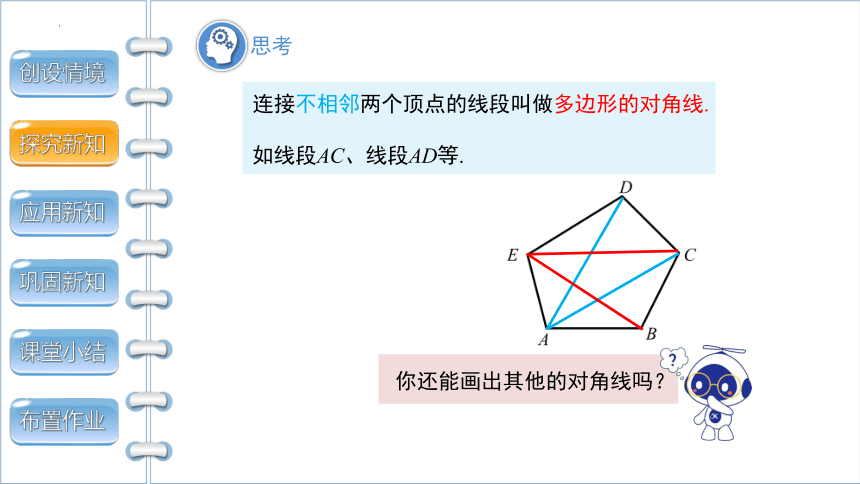
连接不相邻两个顶点的线段叫做多边形的对角线.
如线段AC、线段AD等.
你还能画出其他的对角线吗?
(1) n边形有多少个顶点、多少条边、多少个内角?
三角形
四边形
五边形
六边形
…
… n边形
顶点
边
内角
3 4 5 6 n
3 4 5 6 n
3 4 5 6 n
n边形有n个顶点、n条边、n个内角.
…
…
…
思考
思考
(2)过n边形的每一个顶点有几条对角线?
1
2
3
n-3
对角线数
过n边形的每一个顶点有(n-3)条对角线.
三角形
四边形
五边形
六边形
…
… n边形
0
每个n边形一共有多少条对角线?
一个n边形共有条对角线.
…
思考
(2) 过n边形的每一个顶点有几条对角线?
从一个顶点引出的对角线将n边形分割成(n-2)个三角形.
三角形
四边形
五边形
六边形
…
… n边形
1
2
3 4
n-2
从一个顶点引出的这些对角线把多边形分割成多少个三角形?
三角形个数
…
议一议
观察下图中的多边形,它们的边,角有什么特点?
正三角形 正四边形 正五边形 正六边形 正八边形.
各边相等,各角也相等
这样的多边形叫做正多边形.
思考
现实生活中有许多正多边形的实例,试着举出两例.
螺丝帽的外圈近似于正六边形.
足球上有黑白相间的正五边形.
议一议
上面的图形中有我们熟悉的圆和扇形,你还记得用哪些方法可以画一个圆吗?你能用一根细绳和笔画出一个圆吗?
归纳
如图,平面上,一条线段绕着一个端点旋转一周,另一个端点形成的图形叫做圆.
固定的端点O称为圆心.
线段OA称为半径.
圆上任意两点A,B间的部分叫做圆弧(简称弧).
记作 .读作“圆弧AB”或“弧AB”.
由一条弧AB和经过这条弧的端点的两条半径OA,OB所组成的图形叫做扇形.
顶点在圆心的角叫做圆心角.
A
O
B
AB
做一做
解:因为一个周角为360°,所以分成的三个扇形的圆心角分别是:
360°×60°
360°×=120°
360°×=180°
将一个圆分割成三个扇形,它们的圆心角的度数比为1 : 2 : 3,求这三个扇形的圆心角的度数.
议一议
(1)如图,将一个圆分成三个大小相同的扇形,你能算出它们的圆心角的度数吗?你知道每个扇形的面积和整个圆的面积的关系吗?
它们的圆心角相等,都是120°;
每个扇形的面积是圆形面积的三分之一
结论:
扇形的圆心角与周角的比等于扇形面积与圆的面积的比.
即S扇形= × S圆=
议一议
(2)画一个半径是2cm的圆,并在其中画一个圆心角为60°的扇形,你会计算这个扇形的面积吗?
60°
2 cm
解:S扇形= × S圆
= ×π×22
= π (cm2)
观察如图所示图形,回答下列问题:
(1)从八边形ABCDEFGH的顶点A出发,可以画出多少条对角线?分别用字母表示出来;
(2)这些对角线将八边形分割成多少个三角形?
典型例题
例1
6个
可以画出5条对角线,分别是AC、AD、AE、AF、AG.
分析
经过多边形的一个顶点有(n-3)条对角线,并将多边形分成(n-2)个三角形.
如图,把一个圆平均分成三个扇形,你能求出这三个扇形的圆心角吗?
典型例题
例2
∠AOC=360°×30%=108°
分析
∠AOB=360°×20%=72°
∠BOC=360°×50%=180°
∠AOC=108°
∠AOB=72°
∠BOC=180°
随堂练习
1. 如图所示的图形中,属于多边形的有几个( )
A. 3个 B. 4个
C. 5个 D. 6个
A
随堂练习
2. 一个多边形从一个顶点最多能引出三条对角线,
这个多边形是( )
A. 三角形 B. 四边形
C. 五边形 D. 六边形
3. 在同一个圆中,各扇形的面积之比为1∶1∶3∶4,则
最大扇形的圆心角为( )
A. 120° B. 140°
C. 160° D. 170°
D
C
多边形是由若干条不在同一直线上的线段首尾顺次相连组成的封闭平面图形.
n边形有n个顶点、n条边、n个内角.
过n边形的每一个顶点有(n-3)条对角线,将多边形分割成(n-2)个三角形.
各边相等,各角也相等的多边形叫做正多边形.
平面上,一条线段绕着它的固定的一个端点旋转一周,另一个端点形成的图形叫做圆. 圆上任意两点A,B间的部分叫做圆弧.
由一条弧AB和经过这条弧的端点的两条半径OA,OB所组成的图形叫做扇形.顶点在圆心的角叫做圆心角.
多边形和圆
的初步认识
多边形
圆
教科书第125页
习题4.5
第2、3题
再见
5 多边形和圆的初步认识
配套北师大版
1.经历从现实世界中抽象出平面图形的过程,感受图形世界的丰富多彩.
2.在具体情境中认识多边形、正多边形、圆、扇形.
3.能根据扇形和圆的关系求扇形的圆心角的度数.
4.在丰富的活动中发展学生有条理的思考和表达能力.
学习目标
重点
难点
准备好了吗?一起去探索吧!
多边形和圆的初步认识
同学们,之前学过哪些图形呢?
复习导入
三角形
长方形
正方形
平行四边形
梯形
圆
扇形
图片中哪些是你熟悉的平面图形呢?
情境导入
有三角形、四边形……
有些图形不只有四条边,它们又是什么图形呢?
三角形
四边形
五边形
六边形
这些图形都是多边形.
多边形是由若干条不在同一直线上的线段首尾顺次相连组成的封闭平面图形.
合作探究
如图,在多边形ABCDE中,
点A,B,C,D,E是多边形的顶点;
线段AB,BC,CD,DE,EA是多边形的边;
∠EAB,∠ABC,∠BCD,∠CDE, ∠DEA是多边形的内角.
合作探究
思考
连接不相邻两个顶点的线段叫做多边形的对角线.
如线段AC、线段AD等.
你还能画出其他的对角线吗?
(1) n边形有多少个顶点、多少条边、多少个内角?
三角形
四边形
五边形
六边形
…
… n边形
顶点
边
内角
3 4 5 6 n
3 4 5 6 n
3 4 5 6 n
n边形有n个顶点、n条边、n个内角.
…
…
…
思考
思考
(2)过n边形的每一个顶点有几条对角线?
1
2
3
n-3
对角线数
过n边形的每一个顶点有(n-3)条对角线.
三角形
四边形
五边形
六边形
…
… n边形
0
每个n边形一共有多少条对角线?
一个n边形共有条对角线.
…
思考
(2) 过n边形的每一个顶点有几条对角线?
从一个顶点引出的对角线将n边形分割成(n-2)个三角形.
三角形
四边形
五边形
六边形
…
… n边形
1
2
3 4
n-2
从一个顶点引出的这些对角线把多边形分割成多少个三角形?
三角形个数
…
议一议
观察下图中的多边形,它们的边,角有什么特点?
正三角形 正四边形 正五边形 正六边形 正八边形.
各边相等,各角也相等
这样的多边形叫做正多边形.
思考
现实生活中有许多正多边形的实例,试着举出两例.
螺丝帽的外圈近似于正六边形.
足球上有黑白相间的正五边形.
议一议
上面的图形中有我们熟悉的圆和扇形,你还记得用哪些方法可以画一个圆吗?你能用一根细绳和笔画出一个圆吗?
归纳
如图,平面上,一条线段绕着一个端点旋转一周,另一个端点形成的图形叫做圆.
固定的端点O称为圆心.
线段OA称为半径.
圆上任意两点A,B间的部分叫做圆弧(简称弧).
记作 .读作“圆弧AB”或“弧AB”.
由一条弧AB和经过这条弧的端点的两条半径OA,OB所组成的图形叫做扇形.
顶点在圆心的角叫做圆心角.
A
O
B
AB
做一做
解:因为一个周角为360°,所以分成的三个扇形的圆心角分别是:
360°×60°
360°×=120°
360°×=180°
将一个圆分割成三个扇形,它们的圆心角的度数比为1 : 2 : 3,求这三个扇形的圆心角的度数.
议一议
(1)如图,将一个圆分成三个大小相同的扇形,你能算出它们的圆心角的度数吗?你知道每个扇形的面积和整个圆的面积的关系吗?
它们的圆心角相等,都是120°;
每个扇形的面积是圆形面积的三分之一
结论:
扇形的圆心角与周角的比等于扇形面积与圆的面积的比.
即S扇形= × S圆=
议一议
(2)画一个半径是2cm的圆,并在其中画一个圆心角为60°的扇形,你会计算这个扇形的面积吗?
60°
2 cm
解:S扇形= × S圆
= ×π×22
= π (cm2)
观察如图所示图形,回答下列问题:
(1)从八边形ABCDEFGH的顶点A出发,可以画出多少条对角线?分别用字母表示出来;
(2)这些对角线将八边形分割成多少个三角形?
典型例题
例1
6个
可以画出5条对角线,分别是AC、AD、AE、AF、AG.
分析
经过多边形的一个顶点有(n-3)条对角线,并将多边形分成(n-2)个三角形.
如图,把一个圆平均分成三个扇形,你能求出这三个扇形的圆心角吗?
典型例题
例2
∠AOC=360°×30%=108°
分析
∠AOB=360°×20%=72°
∠BOC=360°×50%=180°
∠AOC=108°
∠AOB=72°
∠BOC=180°
随堂练习
1. 如图所示的图形中,属于多边形的有几个( )
A. 3个 B. 4个
C. 5个 D. 6个
A
随堂练习
2. 一个多边形从一个顶点最多能引出三条对角线,
这个多边形是( )
A. 三角形 B. 四边形
C. 五边形 D. 六边形
3. 在同一个圆中,各扇形的面积之比为1∶1∶3∶4,则
最大扇形的圆心角为( )
A. 120° B. 140°
C. 160° D. 170°
D
C
多边形是由若干条不在同一直线上的线段首尾顺次相连组成的封闭平面图形.
n边形有n个顶点、n条边、n个内角.
过n边形的每一个顶点有(n-3)条对角线,将多边形分割成(n-2)个三角形.
各边相等,各角也相等的多边形叫做正多边形.
平面上,一条线段绕着它的固定的一个端点旋转一周,另一个端点形成的图形叫做圆. 圆上任意两点A,B间的部分叫做圆弧.
由一条弧AB和经过这条弧的端点的两条半径OA,OB所组成的图形叫做扇形.顶点在圆心的角叫做圆心角.
多边形和圆
的初步认识
多边形
圆
教科书第125页
习题4.5
第2、3题
再见
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
