2023-2024学年江西省宜春市丰城九中高一(上)期末数学模拟试卷(含解析)
文档属性
| 名称 | 2023-2024学年江西省宜春市丰城九中高一(上)期末数学模拟试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 159.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-17 14:30:41 | ||
图片预览

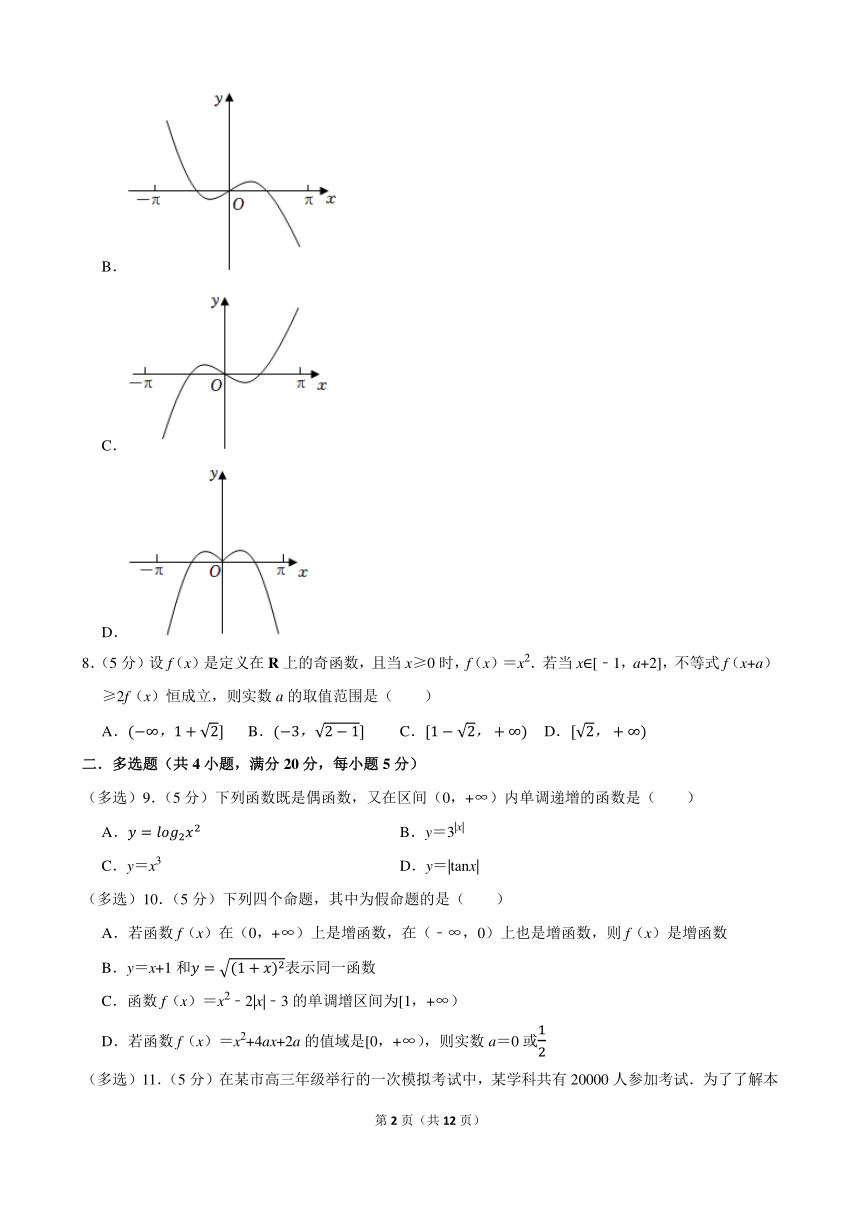



文档简介
2023-2024学年江西省宜春市丰城九中高一(上)期末数学模拟试卷
一.选择题(共8小题,满分40分,每小题5分。在每小题所给出的四个选项中,只有一个选项符合题目要求。)
1.(5分)设集合M={x|log2x<2},N={x|x2﹣3x﹣4≤0},则M∩N=( )
A.{x|0<x<4} B.{x|﹣1≤x≤4} C.{x|﹣1≤x<3} D.{x|0<x≤4}
2.(5分)函数f(x)=x3+5x﹣7的零点所在的区间可以是( )
A.(0,1) B.(1,2) C.(2,3) D.(3,4)
3.(5分)函数的定义域为( )
A.(﹣1,2) B.(0,2) C.[﹣1,2) D.(﹣1,2]
4.(5分)已知定义在(1,+∞)的函数f(x),f′(x)为其导函数,满足f(x)+f'(x)lnx+2x=0,且f(e)=﹣e2,若不等式f(x)≤ax对x∈(1,+∞)恒成立,则实数a的取值范围为( )
A.[﹣e,+∞) B.(﹣e,2) C.[e,+∞) D.(﹣e2,2)
5.(5分)在电话号码薄中任取一个电话号码,则它后边4个数字不相同的概率是( )
A.0.504 B.0.5
C.以上都不对 D.0.648
6.(5分)若f(x+1)=x,且f(x)=5,则x=( )
A.6 B.7 C.8 D.9
7.(5分)函数在(﹣π,π)上的图象大致为( )
A.
B.
C.
D.
8.(5分)设f(x)是定义在R上的奇函数,且当x≥0时,f(x)=x2.若当x∈[﹣1,a+2],不等式f(x+a)≥2f(x)恒成立,则实数a的取值范围是( )
A. B. C. D.
二.多选题(共4小题,满分20分,每小题5分)
(多选)9.(5分)下列函数既是偶函数,又在区间(0,+∞)内单调递增的函数是( )
A. B.y=3|x|
C.y=x3 D.y=|tanx|
(多选)10.(5分)下列四个命题,其中为假命题的是( )
A.若函数f(x)在(0,+∞)上是增函数,在(﹣∞,0)上也是增函数,则f(x)是增函数
B.y=x+1和表示同一函数
C.函数f(x)=x2﹣2|x|﹣3的单调增区间为[1,+∞)
D.若函数f(x)=x2+4ax+2a的值域是[0,+∞),则实数a=0或
(多选)11.(5分)在某市高三年级举行的一次模拟考试中,某学科共有20000人参加考试.为了了解本次考试学生成绩情况,从中抽取了n名学生的成绩(成绩均为正整数,满分为100分)进行统计,其成绩都在区间[50,100]内.按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出频率分布直方图如图所示.其中,成绩落在区间[90,100]内的人数为40,则下列结论正确的是( )
A.n=1000
B.图中x=0.030
C.估计该市全体学生成绩的平均分为84分(同一组数据用该组区间的中点值作代表)
D.若对80分以上的学生授予“优秀学生”称号,则该市约有14000人获得该称号
(多选)12.(5分)已知函数,则( )
A.f(x)的定义域为(﹣2,2)
B.f(x)的图象关于y轴对称
C.f(x)的值域为R
D.f(x)是减函数
三.填空题(共4小题,满分20分,每小题5分)
13.(5分)已知函数,则f(89)= .
14.(5分)若幂函数f(x)=(m2﹣5m+7)xm在R上为增函数,则 .
15.(5分)若函数f(x)是R上的奇函数,则函数y=f(x﹣1)+1的图象必过定点 .
16.(5分)函数的零点个数为 .
四.解答题(共6小题,满分70分)
17.(10分)(1)已知m>0,n>0,不等式x2+mx﹣12<0的解集为(﹣6,n)求实数m,n的值;
(2)正实数a,b满足a+b=2,求的最小值.
18.(12分)在①f(x+1)=f(x)+2x﹣1,②f(x+1)=f(1﹣x),且f(0)=3,③f(x)≥2恒成立,且f(0)=3这三个条件中任选一个,补充在下面的问题中,并作答.问题:已知二次函数f(x)的图像经过点(1,2),_____.
(1)求f(x)的解析式;
(2)求f(x)在[﹣1,+∞)上的值域.
19.(12分)2022年卡塔尔世界杯正赛在北京时间11月21日﹣12月18日进行,赛场内外,丰富的中国元素成为世界杯重要的组成部分,某企业为了解广大球迷世界杯知识的知晓情况.在球迷中开展了网上测试,从大批参与者中随机抽取100名球迷,他们测试得分数据的频率分布直方图如图所示:
(1)根据频率分布直方图,求a的值;
(2)若从得分在[75,90]内的球迷中用分层抽样的方法抽取6人作世界杯知识分享,并在这6人中选取2人担任分享交流活动的主持人,求选取的2人中至少有1名球迷得分在[80,85)内的概率.
20.(12分)某种杂志原以5元每本的价格销售,可以售出8万本.根据市场调查,若单价每提高0.1元,则销售量就相应减少2000本.若把提价后杂志的定价设为x元,则怎样用不等式表示销售的总收入仍不低于20万元?
21.(12分)已知函数,.
(1)求函数f(x)在[0,3]上的值域;
(2)若对任意x1∈[0,3],总存在x2∈[1,+∞),使f(x1)≥g(x2)成立,求实数k的取值范围.
22.(12分)已知函数,a∈R.
(1)若a=0,试判断f(x)的奇偶性,并说明理由;
(2)若函数f(x)在[1,a]上单调,且对任意x∈[1,a],f(x)<﹣2恒成立,求a的取值范围;
(3)若x∈[1,6],当a∈(3,6)时,求函数f(x)的最大值的表达式M(a).
2023-2024学年江西省宜春市丰城九中高一(上)期末数学模拟试卷
参考答案与试题解析
一.选择题(共8小题,满分40分,每小题5分)
1.【解答】解:由log2x<2=log24,得0<x<4,
则M={x|0<x<4},
由x2﹣3x﹣4≤0,得﹣1≤x≤4,
则N={x|﹣1≤x≤4},
所以M∩N={x|0<x<4}.
故选:A.
2.【解答】解:f(0)=﹣7<0,f(1)=1+5﹣7=﹣1<0,f(2)=8+10﹣7=11>0,f(3)=27+15﹣7=35>0,f(4)=64+20﹣7=77>0,
由f(1)f(2)<0,则函数f(x)的零点存在的区间可以是(1,2),
故选:B.
3.【解答】解:由题可知,满足,解得x∈(﹣1,2).
故选:A.
4.【解答】解:令f(x)lnx+x2=C(C为常数),
两边求导数得:
f(x)+f'(x)lnx+2x=0,
∵f(e)=﹣e2,
∴C=0,
∴f(x),
∵不等式f(x)≤ax对x∈(1,+∞)恒成立,
∴ag(x)对x∈(1,+∞)恒成立,
g′(x),
令g′(x)>0,解得:0<x<e,又x>1,故1<x<e,
令g′(x)<0,解得:x>e,
而x∈(1,+∞),故x>1,
故g(x)在(1,e)递增,在(e,+∞)递减,
故g(x)max=g(e)=﹣e,
故a的取值范围是[﹣e,+∞),
故选:A.
5.【解答】解:在电话号码薄中任取一个电话号码,则它后边4个数字一共有104种可能,而4个数字不相同的有种可能,
所以所求概率P0.504,
故选:A.
6.【解答】解:令x+1=t,则x=t﹣1,所以f(t)=t﹣1,
则f(x)=x﹣1,所以x﹣1=5,x=6.
故选:A.
7.【解答】解:∵,x∈(﹣π,π),
∴f(﹣x)=cosx lnf(x),
∴f(x)是奇函数,故排除A、D;
令x,则f()=cos lncos ln7<0,
故排除C;
故选:B.
8.【解答】解:∵f(x)是定义在R上的奇函数,且当x≥0时,f(x)=x2为增函数,
∴当x<0时,f(x)=﹣f(﹣x)=﹣x2为增函数,即f(x)在R上为增函数,
则不等式f(x+a)≥2f(x)等价为不等式f(x+a)≥f(x),
∵f(x)在R上为增函数,
∴x+ax在x∈[﹣1,a+2]上恒成立,
即a≥(1)x,
∵y=(1)x,在x∈[﹣1,a+2]上为增函数,
∴当x=a+2时,y=(1)x取得最大值y=(1)(a+2),
则a≥(1)(a+2)=(1)a+22,
(2)a≥22,
即a,
即实数a的取值范围是[,+∞),
故选:D.
二.多选题(共4小题,满分20分,每小题5分)
9.【解答】解:对于A:设,定义域为{x∈R|x≠0},
∵,
∴为偶函数;
当x∈(0,+∞)时,t=x2为增函数,y=log2t为增函数,
故在区间(0,+∞)内单调递增,故A正确;
对于B:设g(x)=y=3|x|,定义域为R,
又g(﹣x)=3|﹣x|=g(x),则g(x)=y=3|x|为偶函数;
当x∈(0,+∞)时,g(x)=3x为增函数,故B正确;
对于C:y=x3为奇函数,不合题意,故C错误;
对于D:设h(x)=|tanx|,定义域为,
又h(﹣x)=|tan(﹣x)|=h(x),则h(x)为偶函数,
当x∈(0,+∞)时,不妨取,此时h(x)=|tanx|无意义,
故h(x)=|tanx|在区间(0,+∞)内不具有单调性,故D错误.
故选:AB.
10.【解答】解:A中,如f(x)在(0,+∞)上是增函数,在(﹣∞,0)上也是增函数,
但不能说f(x)为增函数,故是假命题;
B中,y=x+1与y=|x+1|的对应关系不同,故是假命题.
C中,画出f(x)的图象如图所示:
可知单调递增区间为[﹣1,0]和[1,+∞),故是假命题;
D中,若函数f(x)=x2+4ax+2a的值域是[0,+∞),
则Δ=16a2﹣8a=0,解得:a=0或x,故D是真命题,
故选:ABC.
11.【解答】解:对于A项,因为成绩落在区间[90,100]内的人数为40,所以,故A项错误;
对于B项,由(0.005+0.010+0.015+x+0.040)×10=1,得x=0.030,故B项正确;
对于C项,学生成绩平均分为:0.005×10×55+0.010×10×65+0.015×10×75+0.030×10×85+0.040×10×95=84,故C项正确;
对于D项,因为20000×(0.04+0.03)×10=14000,故D项正确.
故选:BCD.
12.【解答】解:对于函数,应有0,求得﹣2<x<2,
故f(x)的定义域为(﹣2,2).
根据f(﹣x)=lnlnf(x),可得函数f(x)为奇函数,
图象关于原点对称,故B错误;
再根据t∈(0,+∞),利用对数函数的性质可得,lnt的值域为R,故C正确;
根据x∈(﹣2,2)时,t∈(0,+∞),且t单调递增函数,
故lnt是定义域内的增函数,故D错误,
故选:AC.
三.填空题(共4小题,满分20分,每小题5分)
13.【解答】解:f(89)=f(89+5)=f(94)=f(99)=f(104)=104﹣3=101
故答案为:101
14.【解答】解:因为f(x)=(m2﹣5m+7)xm为幂函数,
所以m2﹣5m+7=1,解得m=2或m=3.
当m=2时,f(x)=x2不满足在R上为增函数,舍去;
当m=3时,f(x)=x3满足在R上为增函数.
故m=3,.
故答案为:.
15.【解答】解:∵函数f(x)是R上的奇函数,
∴函数y=f(x)的图象必过定点(0,0),
∴函数y=f(x﹣1)+1的图象必过定点(1,1),
故答案为:(1,1).
16.【解答】解:函数f(x),
由(x)=0,得,
作出y,y=|lgx|的图象,
可得它们有两个交点,
故函数f(x) 的零点有两个.
故答案为:2.
四.解答题(共6小题,满分70分)
17.【解答】解:(1)由题意可知:﹣6和n是方程x2+mx﹣12=0的两个根,
∴,
解得;
(2)∵正实数a,b满足a+b=2,
∴,
当且仅当,即a=b=1时等号成立.
∴的最小值为2.
18.【解答】解:若选条件①,
(1)设二次函数f(x)=ax2+bx+c(a≠0),
∵f(x+1)=f(x)+2x﹣1,
∴a(x+1)2+b(x+1)+c=ax2+bx+c+2x﹣1,
即ax2+(2a+b)x+a+b+c=ax2+(b+2)x+c﹣1,
又∵二次函数f(x)的图像经过点(1,2),
∴a+b+c=2,
故,
解得a=1,b=﹣2,c=3;
故f(x)=x2﹣2x+3;
(2)f(x)=x2﹣2x+3=(x﹣1)2+2,
∵x∈[﹣1,+∞),
∴f(x)∈[2,+∞),
故f(x)在[﹣1,+∞)上的值域为[2,+∞).
若选条件②,
(1)∵f(x+1)=f(1﹣x),且二次函数f(x)的图像经过点(1,2),
∴设二次函数f(x)=a(x﹣1)2+2(a≠0),
又∵f(0)=3,
∴a+2=3,
故a=1,
故f(x)=(x﹣1)2+2;
(2)f(x)=(x﹣1)2+2,
∵x∈[﹣1,+∞),
∴f(x)∈[2,+∞),
故f(x)在[﹣1,+∞)上的值域为[2,+∞).
若选条件③,
(1)∵f(x)≥2恒成立,且二次函数f(x)的图像经过点(1,2),
∴设二次函数f(x)=a(x﹣1)2+2(a≠0),
又∵f(0)=3,
∴a+2=3,
故a=1,
故f(x)=(x﹣1)2+2;
(2)f(x)=(x﹣1)2+2,
∵x∈[﹣1,+∞),
∴f(x)∈[2,+∞),
故f(x)在[﹣1,+∞)上的值域为[2,+∞).
19.【解答】解:(1)5×(0.01+0.07+0.06+a+0.02)=1,解得:a=0.04.
(2)由分层抽样可知,从得分在[75,80)内的球迷中抽取人,分别记为a1、a2、a3,
从得分在[80,85)内的球迷中抽取人,分别记为b1、b2,
从得分在[85,90)内的球迷中抽取人,记为c.
所以从这6人中选取2人的基本事件有(a1,a2)、(a1,a3)、(a1,b1)、(a1,b2)、(a1,c)、(a2,a3)、(a2,b1)、(a2,b2)、(a2,c)、(a3,b1)、(a3,b2)、(a3,c)、(b1,b2)、(b1,c)、(b2,c),共有15个,
两人中至少有1名球迷得分在[80,85)内的基本事件有(a1,b1)、(a1,b2)、(a2,b1)、(a2,b2)、(a3,b1)、(a3,b2)、(b1,b2)、(b1,c)、(b2,c),共有9个.
所以两人中至少有1名球迷得分在[80,85)内的概率为.
20.【解答】解:把提价后杂志的定价设为x元,则销售量为80.2万本,
则提价后销售的总收入为(80.2)x万元,
那么不等关系“销售的总收入仍不低于20万元”可以表示的不等式为(80.2)x≥20.
21.【解答】解:(1)函数h(x)=x2﹣2x+3=(x﹣1)2+2的开口向上,对称轴为x=1,
所以当0≤x≤3时,h(x)∈[h(1),h(3)]=[2,6].
函数y=2x在R上单调递增,
所以函数f(x)在[0,3]上的值域为[22,26],即[4,64].
(2)由(1)得f(x1)∈[4,64],
,
当x≥1时,,,
所以此时,
若对任意x1∈[0,3],总存在x2∈[1,+∞),使f(x1)≥g(x2)成立,
所以k的取值范围是{k|k≤4}.
22.【解答】解:(1)当a=0时,,所以f(x)为非奇非偶函数;
(2)当x∈[1,a]时,,
因为函数f(x)在[1,a]上单调,所以1<a≤3,
此时f(x)在[1,a]上单调递增,
则,
由题意可知,恒成立,即a2+2a﹣9<0,
所以,
故a的取值范围为(1,);
(3)当x∈[1,6]时,,
又a∈(3,6),由上式可知,f(x)在区间(a,6]单调递增,
当a∈(3,6)时,f(x)在[1,3)上单调递增,在[3,a]上单调递减,
所以f(x)在[1,3)上单调递增,在[3,a]上单调递减,(a,6]上单调递增,
则.
综上所述,函数f(x)的最大值的表达式为.
第1页(共1页)
一.选择题(共8小题,满分40分,每小题5分。在每小题所给出的四个选项中,只有一个选项符合题目要求。)
1.(5分)设集合M={x|log2x<2},N={x|x2﹣3x﹣4≤0},则M∩N=( )
A.{x|0<x<4} B.{x|﹣1≤x≤4} C.{x|﹣1≤x<3} D.{x|0<x≤4}
2.(5分)函数f(x)=x3+5x﹣7的零点所在的区间可以是( )
A.(0,1) B.(1,2) C.(2,3) D.(3,4)
3.(5分)函数的定义域为( )
A.(﹣1,2) B.(0,2) C.[﹣1,2) D.(﹣1,2]
4.(5分)已知定义在(1,+∞)的函数f(x),f′(x)为其导函数,满足f(x)+f'(x)lnx+2x=0,且f(e)=﹣e2,若不等式f(x)≤ax对x∈(1,+∞)恒成立,则实数a的取值范围为( )
A.[﹣e,+∞) B.(﹣e,2) C.[e,+∞) D.(﹣e2,2)
5.(5分)在电话号码薄中任取一个电话号码,则它后边4个数字不相同的概率是( )
A.0.504 B.0.5
C.以上都不对 D.0.648
6.(5分)若f(x+1)=x,且f(x)=5,则x=( )
A.6 B.7 C.8 D.9
7.(5分)函数在(﹣π,π)上的图象大致为( )
A.
B.
C.
D.
8.(5分)设f(x)是定义在R上的奇函数,且当x≥0时,f(x)=x2.若当x∈[﹣1,a+2],不等式f(x+a)≥2f(x)恒成立,则实数a的取值范围是( )
A. B. C. D.
二.多选题(共4小题,满分20分,每小题5分)
(多选)9.(5分)下列函数既是偶函数,又在区间(0,+∞)内单调递增的函数是( )
A. B.y=3|x|
C.y=x3 D.y=|tanx|
(多选)10.(5分)下列四个命题,其中为假命题的是( )
A.若函数f(x)在(0,+∞)上是增函数,在(﹣∞,0)上也是增函数,则f(x)是增函数
B.y=x+1和表示同一函数
C.函数f(x)=x2﹣2|x|﹣3的单调增区间为[1,+∞)
D.若函数f(x)=x2+4ax+2a的值域是[0,+∞),则实数a=0或
(多选)11.(5分)在某市高三年级举行的一次模拟考试中,某学科共有20000人参加考试.为了了解本次考试学生成绩情况,从中抽取了n名学生的成绩(成绩均为正整数,满分为100分)进行统计,其成绩都在区间[50,100]内.按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出频率分布直方图如图所示.其中,成绩落在区间[90,100]内的人数为40,则下列结论正确的是( )
A.n=1000
B.图中x=0.030
C.估计该市全体学生成绩的平均分为84分(同一组数据用该组区间的中点值作代表)
D.若对80分以上的学生授予“优秀学生”称号,则该市约有14000人获得该称号
(多选)12.(5分)已知函数,则( )
A.f(x)的定义域为(﹣2,2)
B.f(x)的图象关于y轴对称
C.f(x)的值域为R
D.f(x)是减函数
三.填空题(共4小题,满分20分,每小题5分)
13.(5分)已知函数,则f(89)= .
14.(5分)若幂函数f(x)=(m2﹣5m+7)xm在R上为增函数,则 .
15.(5分)若函数f(x)是R上的奇函数,则函数y=f(x﹣1)+1的图象必过定点 .
16.(5分)函数的零点个数为 .
四.解答题(共6小题,满分70分)
17.(10分)(1)已知m>0,n>0,不等式x2+mx﹣12<0的解集为(﹣6,n)求实数m,n的值;
(2)正实数a,b满足a+b=2,求的最小值.
18.(12分)在①f(x+1)=f(x)+2x﹣1,②f(x+1)=f(1﹣x),且f(0)=3,③f(x)≥2恒成立,且f(0)=3这三个条件中任选一个,补充在下面的问题中,并作答.问题:已知二次函数f(x)的图像经过点(1,2),_____.
(1)求f(x)的解析式;
(2)求f(x)在[﹣1,+∞)上的值域.
19.(12分)2022年卡塔尔世界杯正赛在北京时间11月21日﹣12月18日进行,赛场内外,丰富的中国元素成为世界杯重要的组成部分,某企业为了解广大球迷世界杯知识的知晓情况.在球迷中开展了网上测试,从大批参与者中随机抽取100名球迷,他们测试得分数据的频率分布直方图如图所示:
(1)根据频率分布直方图,求a的值;
(2)若从得分在[75,90]内的球迷中用分层抽样的方法抽取6人作世界杯知识分享,并在这6人中选取2人担任分享交流活动的主持人,求选取的2人中至少有1名球迷得分在[80,85)内的概率.
20.(12分)某种杂志原以5元每本的价格销售,可以售出8万本.根据市场调查,若单价每提高0.1元,则销售量就相应减少2000本.若把提价后杂志的定价设为x元,则怎样用不等式表示销售的总收入仍不低于20万元?
21.(12分)已知函数,.
(1)求函数f(x)在[0,3]上的值域;
(2)若对任意x1∈[0,3],总存在x2∈[1,+∞),使f(x1)≥g(x2)成立,求实数k的取值范围.
22.(12分)已知函数,a∈R.
(1)若a=0,试判断f(x)的奇偶性,并说明理由;
(2)若函数f(x)在[1,a]上单调,且对任意x∈[1,a],f(x)<﹣2恒成立,求a的取值范围;
(3)若x∈[1,6],当a∈(3,6)时,求函数f(x)的最大值的表达式M(a).
2023-2024学年江西省宜春市丰城九中高一(上)期末数学模拟试卷
参考答案与试题解析
一.选择题(共8小题,满分40分,每小题5分)
1.【解答】解:由log2x<2=log24,得0<x<4,
则M={x|0<x<4},
由x2﹣3x﹣4≤0,得﹣1≤x≤4,
则N={x|﹣1≤x≤4},
所以M∩N={x|0<x<4}.
故选:A.
2.【解答】解:f(0)=﹣7<0,f(1)=1+5﹣7=﹣1<0,f(2)=8+10﹣7=11>0,f(3)=27+15﹣7=35>0,f(4)=64+20﹣7=77>0,
由f(1)f(2)<0,则函数f(x)的零点存在的区间可以是(1,2),
故选:B.
3.【解答】解:由题可知,满足,解得x∈(﹣1,2).
故选:A.
4.【解答】解:令f(x)lnx+x2=C(C为常数),
两边求导数得:
f(x)+f'(x)lnx+2x=0,
∵f(e)=﹣e2,
∴C=0,
∴f(x),
∵不等式f(x)≤ax对x∈(1,+∞)恒成立,
∴ag(x)对x∈(1,+∞)恒成立,
g′(x),
令g′(x)>0,解得:0<x<e,又x>1,故1<x<e,
令g′(x)<0,解得:x>e,
而x∈(1,+∞),故x>1,
故g(x)在(1,e)递增,在(e,+∞)递减,
故g(x)max=g(e)=﹣e,
故a的取值范围是[﹣e,+∞),
故选:A.
5.【解答】解:在电话号码薄中任取一个电话号码,则它后边4个数字一共有104种可能,而4个数字不相同的有种可能,
所以所求概率P0.504,
故选:A.
6.【解答】解:令x+1=t,则x=t﹣1,所以f(t)=t﹣1,
则f(x)=x﹣1,所以x﹣1=5,x=6.
故选:A.
7.【解答】解:∵,x∈(﹣π,π),
∴f(﹣x)=cosx lnf(x),
∴f(x)是奇函数,故排除A、D;
令x,则f()=cos lncos ln7<0,
故排除C;
故选:B.
8.【解答】解:∵f(x)是定义在R上的奇函数,且当x≥0时,f(x)=x2为增函数,
∴当x<0时,f(x)=﹣f(﹣x)=﹣x2为增函数,即f(x)在R上为增函数,
则不等式f(x+a)≥2f(x)等价为不等式f(x+a)≥f(x),
∵f(x)在R上为增函数,
∴x+ax在x∈[﹣1,a+2]上恒成立,
即a≥(1)x,
∵y=(1)x,在x∈[﹣1,a+2]上为增函数,
∴当x=a+2时,y=(1)x取得最大值y=(1)(a+2),
则a≥(1)(a+2)=(1)a+22,
(2)a≥22,
即a,
即实数a的取值范围是[,+∞),
故选:D.
二.多选题(共4小题,满分20分,每小题5分)
9.【解答】解:对于A:设,定义域为{x∈R|x≠0},
∵,
∴为偶函数;
当x∈(0,+∞)时,t=x2为增函数,y=log2t为增函数,
故在区间(0,+∞)内单调递增,故A正确;
对于B:设g(x)=y=3|x|,定义域为R,
又g(﹣x)=3|﹣x|=g(x),则g(x)=y=3|x|为偶函数;
当x∈(0,+∞)时,g(x)=3x为增函数,故B正确;
对于C:y=x3为奇函数,不合题意,故C错误;
对于D:设h(x)=|tanx|,定义域为,
又h(﹣x)=|tan(﹣x)|=h(x),则h(x)为偶函数,
当x∈(0,+∞)时,不妨取,此时h(x)=|tanx|无意义,
故h(x)=|tanx|在区间(0,+∞)内不具有单调性,故D错误.
故选:AB.
10.【解答】解:A中,如f(x)在(0,+∞)上是增函数,在(﹣∞,0)上也是增函数,
但不能说f(x)为增函数,故是假命题;
B中,y=x+1与y=|x+1|的对应关系不同,故是假命题.
C中,画出f(x)的图象如图所示:
可知单调递增区间为[﹣1,0]和[1,+∞),故是假命题;
D中,若函数f(x)=x2+4ax+2a的值域是[0,+∞),
则Δ=16a2﹣8a=0,解得:a=0或x,故D是真命题,
故选:ABC.
11.【解答】解:对于A项,因为成绩落在区间[90,100]内的人数为40,所以,故A项错误;
对于B项,由(0.005+0.010+0.015+x+0.040)×10=1,得x=0.030,故B项正确;
对于C项,学生成绩平均分为:0.005×10×55+0.010×10×65+0.015×10×75+0.030×10×85+0.040×10×95=84,故C项正确;
对于D项,因为20000×(0.04+0.03)×10=14000,故D项正确.
故选:BCD.
12.【解答】解:对于函数,应有0,求得﹣2<x<2,
故f(x)的定义域为(﹣2,2).
根据f(﹣x)=lnlnf(x),可得函数f(x)为奇函数,
图象关于原点对称,故B错误;
再根据t∈(0,+∞),利用对数函数的性质可得,lnt的值域为R,故C正确;
根据x∈(﹣2,2)时,t∈(0,+∞),且t单调递增函数,
故lnt是定义域内的增函数,故D错误,
故选:AC.
三.填空题(共4小题,满分20分,每小题5分)
13.【解答】解:f(89)=f(89+5)=f(94)=f(99)=f(104)=104﹣3=101
故答案为:101
14.【解答】解:因为f(x)=(m2﹣5m+7)xm为幂函数,
所以m2﹣5m+7=1,解得m=2或m=3.
当m=2时,f(x)=x2不满足在R上为增函数,舍去;
当m=3时,f(x)=x3满足在R上为增函数.
故m=3,.
故答案为:.
15.【解答】解:∵函数f(x)是R上的奇函数,
∴函数y=f(x)的图象必过定点(0,0),
∴函数y=f(x﹣1)+1的图象必过定点(1,1),
故答案为:(1,1).
16.【解答】解:函数f(x),
由(x)=0,得,
作出y,y=|lgx|的图象,
可得它们有两个交点,
故函数f(x) 的零点有两个.
故答案为:2.
四.解答题(共6小题,满分70分)
17.【解答】解:(1)由题意可知:﹣6和n是方程x2+mx﹣12=0的两个根,
∴,
解得;
(2)∵正实数a,b满足a+b=2,
∴,
当且仅当,即a=b=1时等号成立.
∴的最小值为2.
18.【解答】解:若选条件①,
(1)设二次函数f(x)=ax2+bx+c(a≠0),
∵f(x+1)=f(x)+2x﹣1,
∴a(x+1)2+b(x+1)+c=ax2+bx+c+2x﹣1,
即ax2+(2a+b)x+a+b+c=ax2+(b+2)x+c﹣1,
又∵二次函数f(x)的图像经过点(1,2),
∴a+b+c=2,
故,
解得a=1,b=﹣2,c=3;
故f(x)=x2﹣2x+3;
(2)f(x)=x2﹣2x+3=(x﹣1)2+2,
∵x∈[﹣1,+∞),
∴f(x)∈[2,+∞),
故f(x)在[﹣1,+∞)上的值域为[2,+∞).
若选条件②,
(1)∵f(x+1)=f(1﹣x),且二次函数f(x)的图像经过点(1,2),
∴设二次函数f(x)=a(x﹣1)2+2(a≠0),
又∵f(0)=3,
∴a+2=3,
故a=1,
故f(x)=(x﹣1)2+2;
(2)f(x)=(x﹣1)2+2,
∵x∈[﹣1,+∞),
∴f(x)∈[2,+∞),
故f(x)在[﹣1,+∞)上的值域为[2,+∞).
若选条件③,
(1)∵f(x)≥2恒成立,且二次函数f(x)的图像经过点(1,2),
∴设二次函数f(x)=a(x﹣1)2+2(a≠0),
又∵f(0)=3,
∴a+2=3,
故a=1,
故f(x)=(x﹣1)2+2;
(2)f(x)=(x﹣1)2+2,
∵x∈[﹣1,+∞),
∴f(x)∈[2,+∞),
故f(x)在[﹣1,+∞)上的值域为[2,+∞).
19.【解答】解:(1)5×(0.01+0.07+0.06+a+0.02)=1,解得:a=0.04.
(2)由分层抽样可知,从得分在[75,80)内的球迷中抽取人,分别记为a1、a2、a3,
从得分在[80,85)内的球迷中抽取人,分别记为b1、b2,
从得分在[85,90)内的球迷中抽取人,记为c.
所以从这6人中选取2人的基本事件有(a1,a2)、(a1,a3)、(a1,b1)、(a1,b2)、(a1,c)、(a2,a3)、(a2,b1)、(a2,b2)、(a2,c)、(a3,b1)、(a3,b2)、(a3,c)、(b1,b2)、(b1,c)、(b2,c),共有15个,
两人中至少有1名球迷得分在[80,85)内的基本事件有(a1,b1)、(a1,b2)、(a2,b1)、(a2,b2)、(a3,b1)、(a3,b2)、(b1,b2)、(b1,c)、(b2,c),共有9个.
所以两人中至少有1名球迷得分在[80,85)内的概率为.
20.【解答】解:把提价后杂志的定价设为x元,则销售量为80.2万本,
则提价后销售的总收入为(80.2)x万元,
那么不等关系“销售的总收入仍不低于20万元”可以表示的不等式为(80.2)x≥20.
21.【解答】解:(1)函数h(x)=x2﹣2x+3=(x﹣1)2+2的开口向上,对称轴为x=1,
所以当0≤x≤3时,h(x)∈[h(1),h(3)]=[2,6].
函数y=2x在R上单调递增,
所以函数f(x)在[0,3]上的值域为[22,26],即[4,64].
(2)由(1)得f(x1)∈[4,64],
,
当x≥1时,,,
所以此时,
若对任意x1∈[0,3],总存在x2∈[1,+∞),使f(x1)≥g(x2)成立,
所以k的取值范围是{k|k≤4}.
22.【解答】解:(1)当a=0时,,所以f(x)为非奇非偶函数;
(2)当x∈[1,a]时,,
因为函数f(x)在[1,a]上单调,所以1<a≤3,
此时f(x)在[1,a]上单调递增,
则,
由题意可知,恒成立,即a2+2a﹣9<0,
所以,
故a的取值范围为(1,);
(3)当x∈[1,6]时,,
又a∈(3,6),由上式可知,f(x)在区间(a,6]单调递增,
当a∈(3,6)时,f(x)在[1,3)上单调递增,在[3,a]上单调递减,
所以f(x)在[1,3)上单调递增,在[3,a]上单调递减,(a,6]上单调递增,
则.
综上所述,函数f(x)的最大值的表达式为.
第1页(共1页)
同课章节目录
