14.1.6 多项式乘多项式 教案 2023--2024学年人教版八年级数学上册
文档属性
| 名称 | 14.1.6 多项式乘多项式 教案 2023--2024学年人教版八年级数学上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 144.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-18 00:00:00 | ||
图片预览




文档简介
第十四章 整式的乘法与因式分解
·14.1.6 多项式乘多项式·
教案
班级: 课时: 课型:
学情分析
学生在进行本节课的学习前已经学习过单项式乘单项式、单项式乘多项式,为本节课学习多项式乘多项式做好了铺垫.
二、教学目标
1.理解多项式与多项式相乘的乘法法则的推导过程;
2.掌握多项式与多项式相乘的乘法法则,能熟练地进行多项式乘法的运算.
三、重点难点
【教学重点】
多项式与多项式相乘的法则及应用.
【教学难点】
综合运用整式乘法法则进行有关化简计算.
四、教学过程设计
第一环节 【复习旧知 引入新课】
师:1.如何进行单项式乘单项式的运算?
生:把它们的系数、相同字母的幂分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式.
单×单= (系数×系数)(同底数幂×同底数幂)(单独的幂)
例子:(-2a2b3c)(3ab)= (-2×3)(a2 a)(b3 b) c= -6a3b4c.
师:2.如何进行单项式乘多项式的运算?
生:单项式与多项式相乘,只要将单项式分别乘以多项式的各项,再将所得的积相加.
例子:p(a+b+c)= pa+pb+pc.
设计意图:通过对已学的知识进行回顾,巩固学生的基础,减小新学知识的难度.
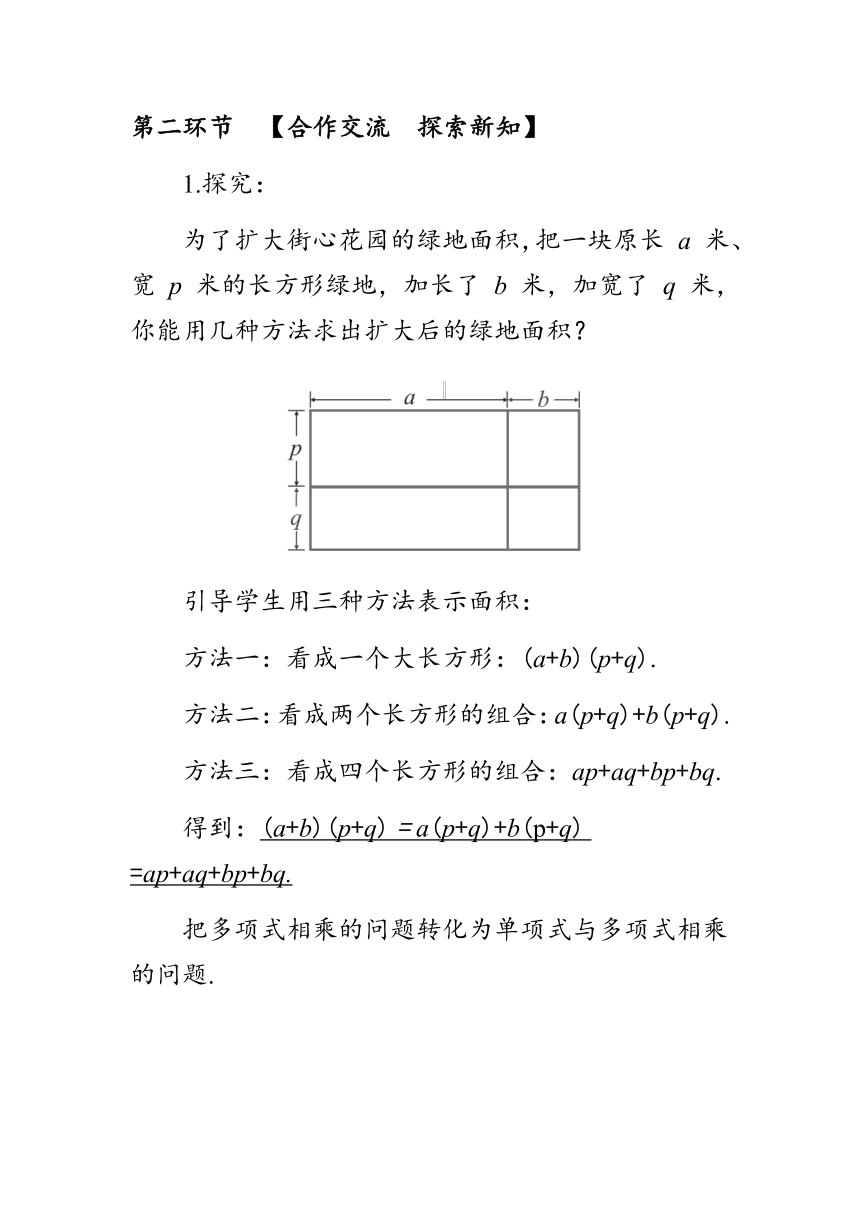
第二环节 【合作交流 探索新知】
1.探究:
为了扩大街心花园的绿地面积,把一块原长 a 米、宽 p 米的长方形绿地,加长了 b 米,加宽了 q 米,你能用几种方法求出扩大后的绿地面积?
引导学生用三种方法表示面积:
方法一:看成一个大长方形:(a+b)(p+q).
方法二:看成两个长方形的组合:a(p+q)+b(p+q).
方法三:看成四个长方形的组合:ap+aq+bp+bq.
得到:(a+b)(p+q) = a(p+q)+b(p+q) =ap+aq+bp+bq.
把多项式相乘的问题转化为单项式与多项式相乘的问题.
师:总体上看,(a+b)(p+q)的结果可以看作由a+b的每一项乘p+q的每一项,再把所得的积相加而得到的,即
得到:多项式与多项式相乘的运算法则:
多项式乘以多项式,先用一个多项式的每一项乘以另一个多项式的每一项,再把所得的积相加.
设计意图:通过用三种不同的方法表示长方形的面积得到相应等式,进而得到多项式乘多项式的法则.
第三环节 【应用迁移 巩固提高】
例1:(1)(3x+1)(x+2),(2)(x-8y)(x-y),
(3)(x+y)(x2-xy+y2).
例2.计算:4y(x+2xy-y) (2x+y 1)[(2y)2+4x].
例3:(1+x)(2x2+ax+1)的结果中不含x2的项,求a的值.
设计意图:本环节结合新课知识对例题进行讲解,让学生进一步掌握多项式乘多项式的法则.
【答案】
例1.解:(1)(3x+1)(x+2)= 3x2+6x+x+2
= 3x2+7x+2;
(2)(x-8y)(x-y)= x2-xy 8xy+8y2
= x2 9xy+8y2;
(3)(x+y)(x2-xy+y2)
= x3-x2y+xy2+x2y-xy2+y3
= x3+y3.
例2.解:原式= 4xy+8xy2-4y2 (2x+y 1)(4y2+4x)
= 4xy+8xy2-4y2 (8xy2+8x2+4y3+4xy-4y2-4x)
= 4xy+8xy2-4y2 8xy2-8x2-4y3-4xy+4y2+4x
= -8x2-4y3+4x.
例3.解:原式 = 2x2+ax+1+2x3+ax2+x
= 2x3+2x2+ax2+x+ax+1
= 2x3+(2+a)x2+(1+a)x+1,
由题意得:2+a = 0,
解得:a = 2.
第四环节 【随堂练习 巩固新知】
1.下列计算结果是x2-5x-6的是( )
A.(x+6)(x-1) B.(x-6)(x+1)
C.(x-2)(x+3) D.(x-3)(x+2)
2.下列计算错误的是( )
A.(x+1)(x+4) = x2+5x+4
B.(m 2)(m+3) = m2+m 6
C.(y+4)(y 5) = y2+9y 20
D.(x 3)(x 6) = x2 9x+18
3.若(x+2)(x-1) = x2+mx+n,则m+n = ( )
A.1 B.-2 C.-1 D.2
4. (2020春 滨海县期中)若长方形的长为a+3b,宽为a+b,则这个长方形的面积为 .
5.计算:
(1)(x+2)(x 3);
(2)(3x 1)(2x+1).
设计意图:通过学生对简单习题的求解,让学生初步接触该课题的知识,巩固好基础,以便求解下一环节的习题.
【答案】
1.B 2.C 3.C 4.a2+4ab+3b2
5.解:(1)(x+2)(x 3)
= x2 3x+2x 6
= x2 x 6;
(2)(3x 1)(2x+1)
= 6x2+3x 2x 1
= 6x2+x 1.
第五环节 【当堂检测 及时反馈】
1.(2020春 太原期中)计算(a+1)(a 3)的结果是( )
A.a2+2a 3 B.a2+2a+3
C.a2 2a 3 D.a2 4a 3
2.(2020春 奉化区期中)如果x+m与x+8 的乘积中不含x的一次项,则m的值是( )
A. 8 B.8 C.0 D.1
3.(2019秋 白云区期末)化简(x+4)(x 1)+(x 4)(x+1)的结果是( )
A.2x2 8 B.2x2 x 4
C.2x2+8 D.2x2+6x
4.(2020春 遵化市期中)如果关于x的多项式(2x m)与(x+5)的乘积中,常数项为 15,则m的值为( )
A.3 B. 3 C.10 D. l0
5.(2019秋 太仆寺旗期末)若多项式(x+1)(x 3) = x2+ax+b,则a,b的值分别是( )
A.a = 2,b = 3 B.a = 2,b = 3
C.a = 2,b = 3 D.a = 2,b = 3
6.(2019秋 武昌区校级月考)已知(x2+px+8)(x2 3x+q)展开后不含x2与x3的项,则qp = .
7.如图,长方形的长为a,宽为b,横、纵向阴影部分均为长方形,它们的宽都为c,则空白部分的面积是 .
8.(2020春 青羊区期末)已知x2+x =3,则代数式(x+4)(x﹣3)的值为 .
9.(2019秋 大荔县期末)已知a+b = 4,ab = 3,求代数式 (a+2)(b+2)的值.
10.(2019春 沙坪坝区校级月考)若(2x2 mx+6)(x2 3x+3n)的展开式中x2项的系数为 9,x3项的系数为 1,求m-n的值.
设计意图:本环节的练习层次较高,主要考察学生对本课的掌握程度,以此反馈本课的学习质量,便于教师调整教学.
【答案】
C 2.A 3.A 4.B 5.B
6.1 7.ab-bc-ac+c2 8.-9
解:原式 = ab+2a+2b+4
= ab+2(a+b) +4 ,
当a+b = 4,ab = 3时,
∴ 原式 = 3+8+4= 15.
10.解:(2x2 mx+6)(x2 3x+3n)
= 2x4 (m+6)x3+(6n+3m+6)x2 3(6+mn)x+18n,
∵ 展开式中x2项的系数为9,x3项的系数为1,
∴ 6n+3m+6 = 9,m+6 = 1.
解得m = 7,n = 4.
∴ m n = 7 4= 11.
第六环节 【拓展延伸 能力提升】
1.甲、乙二人共同计算整式乘法(2x+a)(3x+b).由于甲抄错了第一个多项式中a的符号,得到的结果为 6x2+11x-10;由于乙漏抄了第二个多项式中x的系数,得到的结果为 2x2-9x+10.
(1)你能知道式子中a,b的值各是多少吗?
(2)请你计算出这道整式乘法的正确结果.
2.计算: ①(x+2)(x+3); ②(x-4)(x+1);
③(y+4)(y-2) ; ④(y-5)(y-3).
(1)由前面计算的结果找规律,观察右图,填空:
(x+p)(x+q)=( )2+( )x+( )
(2)根据上述求解过程,观察计算结果的各项系数与原式中的系数有怎样的关系?
(3)根据上述结论计算:
①(x+1)(x+2) = ;
②(x+1)(x-2) = ;
③(x-1)(x+2) = ;
④(x-1)(x-2) = .
设计意图:本环节主要考察学生能否灵活运用本课知识求解综合性较高的习题,了解学生的掌握程度,展现了教学有梯度的理念.
【答案】
1.解:(1)由题意知,甲做的整式乘法的式子为(2x-a)(3x+b),
乙做的整式乘法的式子为(2x+a)(x+b).
(2x-a)(3x+b) = 6x2-(3a-2b)x-ab = 6x2+11x-10.
(2x+a)(x+b) = 2x2+(a+2b)x+ab = 2x2-9x+10.
∴-(3a-2b)= 11, a+2b=-9,
解得:a=-5,b=-2.
(2)(2x+a)(3x+b)
= (2x-5)(3x-2)
= 6x2-19x+10.
2.①(x+2)(x+3) = x2+5x+6;
②(x-4)(x+1) = x2-3x-4;
③(y+4)(y-2) = y2+2y-8;
④(y-5)(y-3)= y2-8y+15.
(1)x,p+q,pq.
(2)(x+p)(x+q) = x2+(p+q)x+pq.
(3)①(x+1)(x+2) = x2+3x+2;
②(x+1)(x-2) = x2-x-2;
③(x-1)(x+2) = x2+x-2;
④(x-1)(x-2) =x2-3x+2.
第七环节 【总结反思 知识内化】
课堂小结:多项式与多项式相乘的法则:
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
注意:运算结果一定要合并同类项.
设计意图:通过知识小结,使学生梳理本节课所学内容,理解本课核心知识,提高学习质量.
第八环节 【布置作业 夯实基础】
·14.1.6 多项式乘多项式·
教案
班级: 课时: 课型:
学情分析
学生在进行本节课的学习前已经学习过单项式乘单项式、单项式乘多项式,为本节课学习多项式乘多项式做好了铺垫.
二、教学目标
1.理解多项式与多项式相乘的乘法法则的推导过程;
2.掌握多项式与多项式相乘的乘法法则,能熟练地进行多项式乘法的运算.
三、重点难点
【教学重点】
多项式与多项式相乘的法则及应用.
【教学难点】
综合运用整式乘法法则进行有关化简计算.
四、教学过程设计
第一环节 【复习旧知 引入新课】
师:1.如何进行单项式乘单项式的运算?
生:把它们的系数、相同字母的幂分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式.
单×单= (系数×系数)(同底数幂×同底数幂)(单独的幂)
例子:(-2a2b3c)(3ab)= (-2×3)(a2 a)(b3 b) c= -6a3b4c.
师:2.如何进行单项式乘多项式的运算?
生:单项式与多项式相乘,只要将单项式分别乘以多项式的各项,再将所得的积相加.
例子:p(a+b+c)= pa+pb+pc.
设计意图:通过对已学的知识进行回顾,巩固学生的基础,减小新学知识的难度.
第二环节 【合作交流 探索新知】
1.探究:
为了扩大街心花园的绿地面积,把一块原长 a 米、宽 p 米的长方形绿地,加长了 b 米,加宽了 q 米,你能用几种方法求出扩大后的绿地面积?
引导学生用三种方法表示面积:
方法一:看成一个大长方形:(a+b)(p+q).
方法二:看成两个长方形的组合:a(p+q)+b(p+q).
方法三:看成四个长方形的组合:ap+aq+bp+bq.
得到:(a+b)(p+q) = a(p+q)+b(p+q) =ap+aq+bp+bq.
把多项式相乘的问题转化为单项式与多项式相乘的问题.
师:总体上看,(a+b)(p+q)的结果可以看作由a+b的每一项乘p+q的每一项,再把所得的积相加而得到的,即
得到:多项式与多项式相乘的运算法则:
多项式乘以多项式,先用一个多项式的每一项乘以另一个多项式的每一项,再把所得的积相加.
设计意图:通过用三种不同的方法表示长方形的面积得到相应等式,进而得到多项式乘多项式的法则.
第三环节 【应用迁移 巩固提高】
例1:(1)(3x+1)(x+2),(2)(x-8y)(x-y),
(3)(x+y)(x2-xy+y2).
例2.计算:4y(x+2xy-y) (2x+y 1)[(2y)2+4x].
例3:(1+x)(2x2+ax+1)的结果中不含x2的项,求a的值.
设计意图:本环节结合新课知识对例题进行讲解,让学生进一步掌握多项式乘多项式的法则.
【答案】
例1.解:(1)(3x+1)(x+2)= 3x2+6x+x+2
= 3x2+7x+2;
(2)(x-8y)(x-y)= x2-xy 8xy+8y2
= x2 9xy+8y2;
(3)(x+y)(x2-xy+y2)
= x3-x2y+xy2+x2y-xy2+y3
= x3+y3.
例2.解:原式= 4xy+8xy2-4y2 (2x+y 1)(4y2+4x)
= 4xy+8xy2-4y2 (8xy2+8x2+4y3+4xy-4y2-4x)
= 4xy+8xy2-4y2 8xy2-8x2-4y3-4xy+4y2+4x
= -8x2-4y3+4x.
例3.解:原式 = 2x2+ax+1+2x3+ax2+x
= 2x3+2x2+ax2+x+ax+1
= 2x3+(2+a)x2+(1+a)x+1,
由题意得:2+a = 0,
解得:a = 2.
第四环节 【随堂练习 巩固新知】
1.下列计算结果是x2-5x-6的是( )
A.(x+6)(x-1) B.(x-6)(x+1)
C.(x-2)(x+3) D.(x-3)(x+2)
2.下列计算错误的是( )
A.(x+1)(x+4) = x2+5x+4
B.(m 2)(m+3) = m2+m 6
C.(y+4)(y 5) = y2+9y 20
D.(x 3)(x 6) = x2 9x+18
3.若(x+2)(x-1) = x2+mx+n,则m+n = ( )
A.1 B.-2 C.-1 D.2
4. (2020春 滨海县期中)若长方形的长为a+3b,宽为a+b,则这个长方形的面积为 .
5.计算:
(1)(x+2)(x 3);
(2)(3x 1)(2x+1).
设计意图:通过学生对简单习题的求解,让学生初步接触该课题的知识,巩固好基础,以便求解下一环节的习题.
【答案】
1.B 2.C 3.C 4.a2+4ab+3b2
5.解:(1)(x+2)(x 3)
= x2 3x+2x 6
= x2 x 6;
(2)(3x 1)(2x+1)
= 6x2+3x 2x 1
= 6x2+x 1.
第五环节 【当堂检测 及时反馈】
1.(2020春 太原期中)计算(a+1)(a 3)的结果是( )
A.a2+2a 3 B.a2+2a+3
C.a2 2a 3 D.a2 4a 3
2.(2020春 奉化区期中)如果x+m与x+8 的乘积中不含x的一次项,则m的值是( )
A. 8 B.8 C.0 D.1
3.(2019秋 白云区期末)化简(x+4)(x 1)+(x 4)(x+1)的结果是( )
A.2x2 8 B.2x2 x 4
C.2x2+8 D.2x2+6x
4.(2020春 遵化市期中)如果关于x的多项式(2x m)与(x+5)的乘积中,常数项为 15,则m的值为( )
A.3 B. 3 C.10 D. l0
5.(2019秋 太仆寺旗期末)若多项式(x+1)(x 3) = x2+ax+b,则a,b的值分别是( )
A.a = 2,b = 3 B.a = 2,b = 3
C.a = 2,b = 3 D.a = 2,b = 3
6.(2019秋 武昌区校级月考)已知(x2+px+8)(x2 3x+q)展开后不含x2与x3的项,则qp = .
7.如图,长方形的长为a,宽为b,横、纵向阴影部分均为长方形,它们的宽都为c,则空白部分的面积是 .
8.(2020春 青羊区期末)已知x2+x =3,则代数式(x+4)(x﹣3)的值为 .
9.(2019秋 大荔县期末)已知a+b = 4,ab = 3,求代数式 (a+2)(b+2)的值.
10.(2019春 沙坪坝区校级月考)若(2x2 mx+6)(x2 3x+3n)的展开式中x2项的系数为 9,x3项的系数为 1,求m-n的值.
设计意图:本环节的练习层次较高,主要考察学生对本课的掌握程度,以此反馈本课的学习质量,便于教师调整教学.
【答案】
C 2.A 3.A 4.B 5.B
6.1 7.ab-bc-ac+c2 8.-9
解:原式 = ab+2a+2b+4
= ab+2(a+b) +4 ,
当a+b = 4,ab = 3时,
∴ 原式 = 3+8+4= 15.
10.解:(2x2 mx+6)(x2 3x+3n)
= 2x4 (m+6)x3+(6n+3m+6)x2 3(6+mn)x+18n,
∵ 展开式中x2项的系数为9,x3项的系数为1,
∴ 6n+3m+6 = 9,m+6 = 1.
解得m = 7,n = 4.
∴ m n = 7 4= 11.
第六环节 【拓展延伸 能力提升】
1.甲、乙二人共同计算整式乘法(2x+a)(3x+b).由于甲抄错了第一个多项式中a的符号,得到的结果为 6x2+11x-10;由于乙漏抄了第二个多项式中x的系数,得到的结果为 2x2-9x+10.
(1)你能知道式子中a,b的值各是多少吗?
(2)请你计算出这道整式乘法的正确结果.
2.计算: ①(x+2)(x+3); ②(x-4)(x+1);
③(y+4)(y-2) ; ④(y-5)(y-3).
(1)由前面计算的结果找规律,观察右图,填空:
(x+p)(x+q)=( )2+( )x+( )
(2)根据上述求解过程,观察计算结果的各项系数与原式中的系数有怎样的关系?
(3)根据上述结论计算:
①(x+1)(x+2) = ;
②(x+1)(x-2) = ;
③(x-1)(x+2) = ;
④(x-1)(x-2) = .
设计意图:本环节主要考察学生能否灵活运用本课知识求解综合性较高的习题,了解学生的掌握程度,展现了教学有梯度的理念.
【答案】
1.解:(1)由题意知,甲做的整式乘法的式子为(2x-a)(3x+b),
乙做的整式乘法的式子为(2x+a)(x+b).
(2x-a)(3x+b) = 6x2-(3a-2b)x-ab = 6x2+11x-10.
(2x+a)(x+b) = 2x2+(a+2b)x+ab = 2x2-9x+10.
∴-(3a-2b)= 11, a+2b=-9,
解得:a=-5,b=-2.
(2)(2x+a)(3x+b)
= (2x-5)(3x-2)
= 6x2-19x+10.
2.①(x+2)(x+3) = x2+5x+6;
②(x-4)(x+1) = x2-3x-4;
③(y+4)(y-2) = y2+2y-8;
④(y-5)(y-3)= y2-8y+15.
(1)x,p+q,pq.
(2)(x+p)(x+q) = x2+(p+q)x+pq.
(3)①(x+1)(x+2) = x2+3x+2;
②(x+1)(x-2) = x2-x-2;
③(x-1)(x+2) = x2+x-2;
④(x-1)(x-2) =x2-3x+2.
第七环节 【总结反思 知识内化】
课堂小结:多项式与多项式相乘的法则:
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
注意:运算结果一定要合并同类项.
设计意图:通过知识小结,使学生梳理本节课所学内容,理解本课核心知识,提高学习质量.
第八环节 【布置作业 夯实基础】
