13.4 课题学习—最短路径问题教案 2023-2024学年人教版八年级数学上册
文档属性
| 名称 | 13.4 课题学习—最短路径问题教案 2023-2024学年人教版八年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-18 20:08:38 | ||
图片预览



文档简介
第十三章 轴对称
·13.4 课题学习—最短路径问题·
教案
班级: 课时: 课型:
学情分析
学生已经学习了轴对称的知识以及三角形两边之和大于第三边的知识,七年级时也学习了对于直线异侧的两点,怎样在直线上找到一点,使这一点到这两点的距离之和最小,学生很容易想到连接这两点,所连线段与直线的交点就是所求的点.但对于直线同侧的两点,如何在直线上找到一点,使这一点到这两点的距离之和最小,这就需要用到轴对称的知识.
二、教学目标
1.能利用轴对称解决简单的最短路径问题.
2.在探究最短路径的过程中,体会“轴对称”的桥梁作用,感悟转化的数学思想.
三、重点难点
【教学重点】
利用轴对称将最短路径问题转化为“两点之间、线段最短”问题.
【教学难点】
如何利用轴对称将最短路径问题转化为线段和最小问题.
四、教学过程设计
第一环节 【创设情境 引入新课】
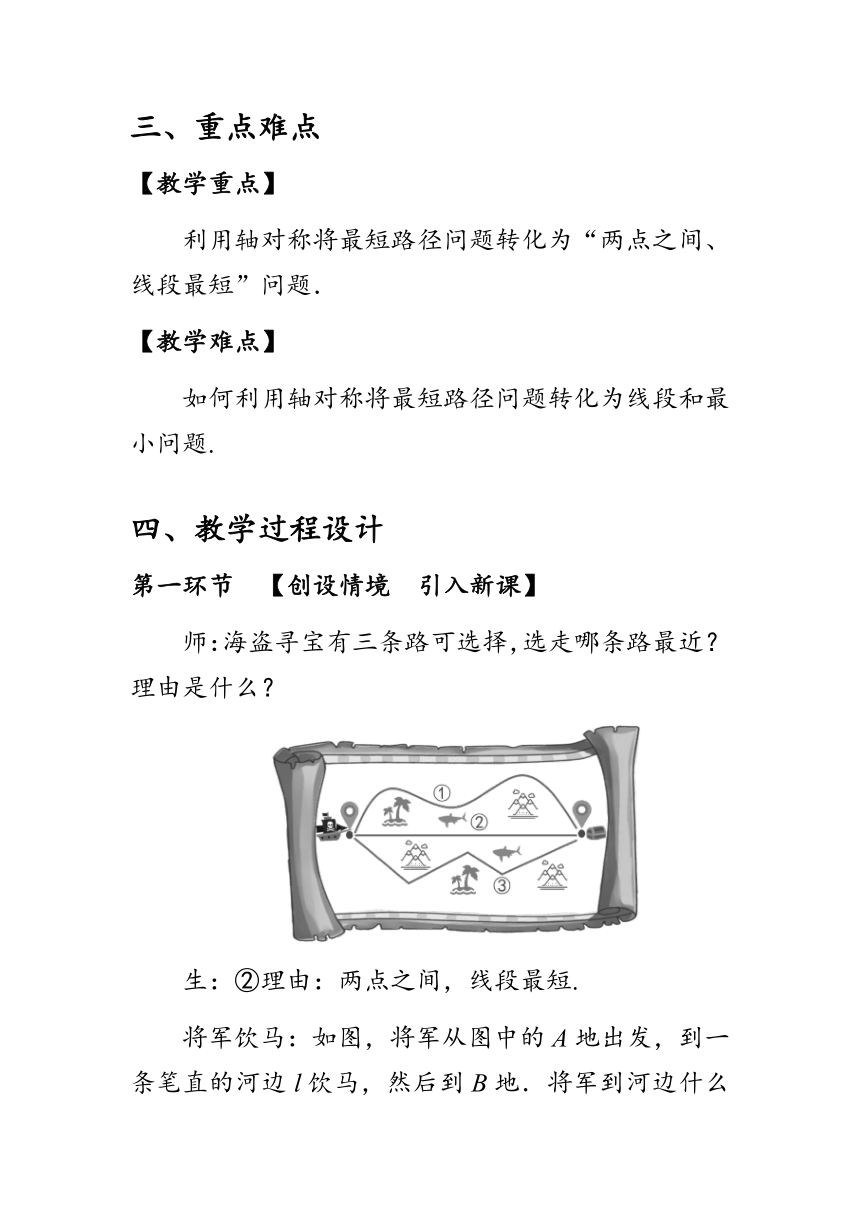
师:海盗寻宝有三条路可选择,选走哪条路最近?理由是什么?
生:②理由:两点之间,线段最短.
将军饮马:如图,将军从图中的A地出发,到一条笔直的河边l饮马,然后到B地.将军到河边什么地方饮马,可使所走的路径最短?(引出课题)
设计意图:利用“海盗寻宝”、“将军饮马”两个小故事吸引学生注意力,提高学习兴趣并引出路径最短问题.
第二环节 【合作交流 探索新知】
师:你能把“将军饮马”的问题抽象为数学问题吗?
将A,B两地抽象为两个点,将河流l抽象为一条直线.
问题转化为:当点C在l的什么位置时,使得AC与CB的和最小.
探究1:两点在直线异侧
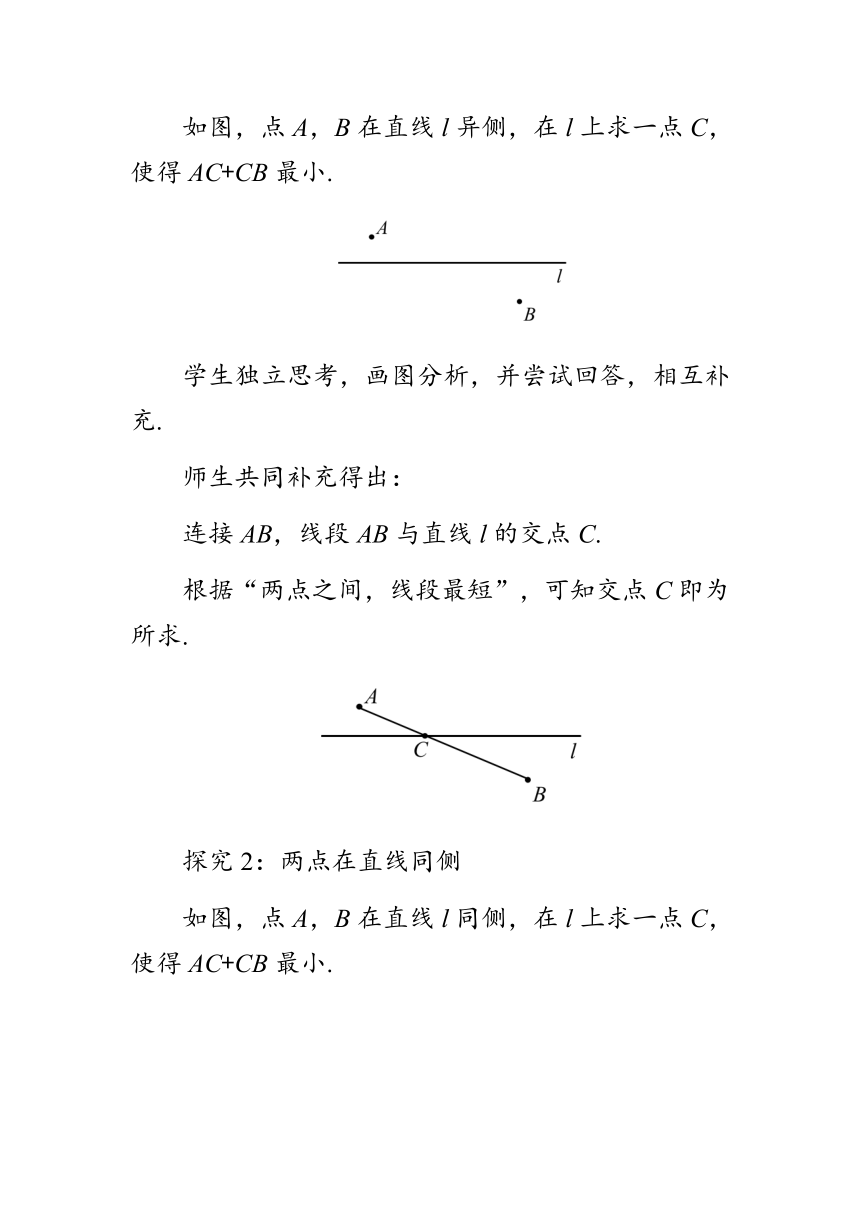
如图,点A,B在直线l异侧,在l上求一点C,使得AC+CB最小.
学生独立思考,画图分析,并尝试回答,相互补充.
师生共同补充得出:
连接AB,线段AB与直线l的交点C.
根据“两点之间,线段最短”,可知交点C即为所求.
探究2:两点在直线同侧
如图,点A,B在直线l同侧,在l上求一点C,使得AC+CB最小.
学生独立思考,画图分析,并尝试回答,相互补充.
教师可提醒:将B点移到直线的另一侧转化为“两点在直线异侧”的情况.
师生共同补充得出:
(1)作点B关于直线l的对称点B′;
(2)连接AB′,与直线l相交于点C.则点C即为所求.
师:你能用所学的知识证明AC+BC最短吗?
师生共同分析,然后学生说明证明过程,教师板书:
证明:如图,在直线l 上任取一点C′(与点C不重合),
连接AC′,BC′,B′C′.
由轴对称的性质知,BC = B′C,BC′ = B′C′.
∴ AC+BC = AC+B′C = AB′,
AC′+BC′ = AC′+B′C′.
在△AB′C′中,AB′<AC′+B′C′,
∴ AC+BC<AC′+BC′.
即AC+BC最短.
总结:
最短路径问题
两点在直线同侧:两点连线与直线的交点.
两点在直线异侧:一点与另一点关于直线的对称点的连线与直线的交点.
原理:两点之间,线段最短.
设计意图:从异侧问题入手,由简到难,逐步深入,将同侧问题转化为异侧问题,渗透转化思想.
第三环节 【应用迁移 巩固提高】
例1.如图牧马人从A地出发,先到草地边某一处牧马,再到河边饮马,然后回到B处,请画出最短路径.
例2.架桥问题:如图,A、B两地在一条河的两岸,现要在河上造一座桥MN,桥造在何处可使从A到B的路径AMNB最短?(假定河的两岸是平行的直线,桥要与河垂直)
例3.如图,点P在∠AOB内部,问如何在射线OA、OB上分别找点C、D,使PC+CD+DP之和最小?
设计意图:对前面所学的解题方法与思路得以巩固,让学生形成技能,进一步体会感悟数学中的转化思想.
【答案】
例1.解:如图所示,分别作出点A关于MN的对称点A1,点B关于l对称点B1,
连接A1 B1,与MN和l分别交于点C,D,
则线路ACDB即为所求.
例2.解:如图所示,把河的两岸看成两条平行线a和b,
N为直线b上的一个动点,MN垂直于直线b,交直线a于点M.
问题转化为:当点N在b的什么位置时,AM+MN+NB最小,
因为河的宽度MN是固定的,问题转化为:
当点N在b的什么位置时,AM+NB最小.
将AM沿与河岸垂直的方向平移,
点M移动到点N,点A移动到点A',
则A'A = MN,
AM+NB = A'N+NB.
问题转化为:当点N在b的什么位置时,A'N+NB最小.
如图,在连接A',B两点的线中,线段A'B最短.
因此,线段A'B与直线b的交点N的位置即为所求.
即在点N处造桥MN,所得路径AMNB是最短的.
例3.解:如图,分别作点P关于OA,OB的对
称点P1,P2,
连接P1P2分别与OA,OB交于点C,D,
所得PC+CD+DP之和最小.
第四环节 【随堂练习 巩固新知】
1.如图,小明到小丽家有四条路,其中路程最短的是( )
① B.② C.③ D.④
2.如图,某村计划挖一条水渠将不远处的河水引到农田(记作点O),以便对农田进行灌溉,现设计了四条路线,其中最短的是( )
A.OA B.OB C.OC D.OD
3.如图,直线l是一条河,P,Q是两个村庄,欲在l上的某处修建一个水泵站,分别向P,Q两地供水,现有如下四种铺设方案,图中实线表示铺设的管道,则所需管道最短的是( )
如图,在四边形ABCD中,∠A = 90°,AD = 4,连接BD,BD⊥CD,∠ADB = ∠C,若P是BC边上一动点,则DP长的最小值为____.
如图,AD是等边△ABC的BC边上的高,AD = 6,M是AD上的动点,E是AC边的中点,则EM+CM的最小值为____.
设计意图:本环节主要考察学生对新学知识的理解及掌握情况.
【答案】
1.B 2.B 3.D 4.4 5.6
第五环节 【当堂检测 及时反馈】
1.(2020春 汉阳区期中)点P为直线l外一点,点A,B, C为直线l上三点,PA = 3 cm,PB = 4 cm,PC = 5 cm,则点P到直线l的距离( )
A.等于 4 cm B.等于 3 cm
C.小于 3 cm D.不大于 3 cm
2.(2019秋 浦北县期末)如图,等边△ABC的边长为 8,AD是BC边上的中线,E是AD边上的动点,F是AB边上一点,若BF = 4,当BE+EF取得最小值时,则∠EBC的度数为( )
A.15° B.25° C.30° D.45°
如图,四边形ABCD中,∠C = 50°,∠B = ∠D = 90°,E,F分别是BC,DC上的点,当△AEF的周长最小时,∠EAF的度数为( )
A.50° B.60° C.70° D.80°
4.(2019秋 武汉期中)如图,A、B是直线CD外两定点,P为直线CD上一动点,当PB-PA最大时,∠BPC = 40°.此时∠APC的度数为( )
A.40° B.80° C.100° D.140°
5.(2020春 和平区期末)如图,若∠MON = 42°,P为∠MON内一定点,OM上有一点A,ON上有一点B,当△PAB的周长取最小值时,则∠APB的度数为 .
6.(2020秋 双流区校级月考)如图,∠ABC = 30°,点D是∠ABC内的一点,且DB = 9,若点E,F分别是射线BA,BC上异于点B的动点,则△DEF的周长的最小值是 .
7.(2019秋 忻州期末)如图,在△ABC中,AB = AC,BC = 4,S△ABC = 12,点D,E分别是AB,BC的中点,点F在AC上,且FD⊥AB.若点P为线段DF上一动点,连接BP,EP,则△BPE周长的最小值是 .
8.(2019秋 梁子湖区期末)如图,∠AOB = 30°,M,N分别是OA,OB上的定点,P,Q分别是边OB,OA上的动点,如果记∠AMP = α,∠ONQ = β,当MP+PQ+QN最小时,则α与β的数量关系是 .
9.如图,要在街道l上修建一个奶吧D(街道用直线l表示).
(1)若奶吧D向小区A,B提供牛奶如图①,则奶吧D应建在什么地方,才能使它到小区A,B的距离之和最短?
(2)若奶吧D向小区A,C提供牛奶如图②,则奶吧D应建在什么地方,才能使它到小区A,C的距离之和最短?
10.如图,荆州护城河在CC'处直角转弯,河宽相等,从A处到达B处,需经两座桥(桥宽不计),设护城河以及两座桥都是东西、南北方向的,试问:桥架在何处,才能使从A到B的距离最短?
设计意图:通过小测反馈本节课学生对知识的掌握情况.
【答案】
D 2.C 3.D 4.A 5.96° 6.9
7.8 8.α-β = 90°
9.解:(1)连接AB与直线l交于点D,
奶吧D的位置如图①所示;
(2)作点A关于直线l的对称点A′,
连接A′C与直线l交于点D,
奶吧D的位置如图②所示.
10.解:作AF⊥河岸,且AF = 河宽,
作BG⊥河岸,且BG = 河宽,
连接GF,与河岸相交于E′、D′.
作DD′⊥河岸, EE′⊥河岸,
DD′、EE′即为桥的位置.
由两点之间线段最短可知,GF最小;
即当桥建于如图所示位置时,才能使从A到B的距离最短.
第六环节 【拓展延伸 能力提升】
1.如图,已知△ABC为等腰直角三角形,AC = BC = 4,∠BCD = 15°,P为CD上的动点,则|PA-PB|的最大值为 .
2.如图,AB⊥BC,AD⊥DC,∠BAD = 100°,在BC、CD上分别找一点M、N,当△AMN周长最小时,求∠MAN的度数是多少?
设计意图:通过有梯度的训练,提高学生对知识的综合运用能力.
【答案】
1.4
2.解:作A关于BC和CD的对称点A′,A″,连接A′A″,
交BC于M,交CD于N,则A′A″即为△AMN的周长最小值.
∵ ∠DAB = 100°,
∴ ∠AA′M+∠A″ = 180°-∠BAD = 180°-100°= 80°,
∵ ∠MA′A = ∠MAA′,∠NAD = ∠A″,
且∠MA′A+∠MAA′ = ∠AMN,∠NAD+∠A″ = ∠ANM,
∴ ∠AMN+∠ANM = ∠MA′A+∠MAA′+∠NAD+∠A″
= 2(∠AA′M+∠A″) = 2×80°= 160°,
∠MAN = 180°-160°= 20°.
故当△AMN周长最小时,∠MAN的度数是 20°.
第七环节 【总结反思 知识内化】
课堂小结:
这节课我们学到了什么?
两点在直线同侧:两点连线与直线的交点.
两点在直线异侧:一点与另一点关于直线的对称点的连线与直线的交点.
造桥选址:垂直河岸方向平移,使其他线段共线.
设计意图:使学生系统地了解本课核心知识,加深理解,建立内在联系.
第八环节 【布置作业 夯实基础】
·13.4 课题学习—最短路径问题·
教案
班级: 课时: 课型:
学情分析
学生已经学习了轴对称的知识以及三角形两边之和大于第三边的知识,七年级时也学习了对于直线异侧的两点,怎样在直线上找到一点,使这一点到这两点的距离之和最小,学生很容易想到连接这两点,所连线段与直线的交点就是所求的点.但对于直线同侧的两点,如何在直线上找到一点,使这一点到这两点的距离之和最小,这就需要用到轴对称的知识.
二、教学目标
1.能利用轴对称解决简单的最短路径问题.
2.在探究最短路径的过程中,体会“轴对称”的桥梁作用,感悟转化的数学思想.
三、重点难点
【教学重点】
利用轴对称将最短路径问题转化为“两点之间、线段最短”问题.
【教学难点】
如何利用轴对称将最短路径问题转化为线段和最小问题.
四、教学过程设计
第一环节 【创设情境 引入新课】
师:海盗寻宝有三条路可选择,选走哪条路最近?理由是什么?
生:②理由:两点之间,线段最短.
将军饮马:如图,将军从图中的A地出发,到一条笔直的河边l饮马,然后到B地.将军到河边什么地方饮马,可使所走的路径最短?(引出课题)
设计意图:利用“海盗寻宝”、“将军饮马”两个小故事吸引学生注意力,提高学习兴趣并引出路径最短问题.
第二环节 【合作交流 探索新知】
师:你能把“将军饮马”的问题抽象为数学问题吗?
将A,B两地抽象为两个点,将河流l抽象为一条直线.
问题转化为:当点C在l的什么位置时,使得AC与CB的和最小.
探究1:两点在直线异侧
如图,点A,B在直线l异侧,在l上求一点C,使得AC+CB最小.
学生独立思考,画图分析,并尝试回答,相互补充.
师生共同补充得出:
连接AB,线段AB与直线l的交点C.
根据“两点之间,线段最短”,可知交点C即为所求.
探究2:两点在直线同侧
如图,点A,B在直线l同侧,在l上求一点C,使得AC+CB最小.
学生独立思考,画图分析,并尝试回答,相互补充.
教师可提醒:将B点移到直线的另一侧转化为“两点在直线异侧”的情况.
师生共同补充得出:
(1)作点B关于直线l的对称点B′;
(2)连接AB′,与直线l相交于点C.则点C即为所求.
师:你能用所学的知识证明AC+BC最短吗?
师生共同分析,然后学生说明证明过程,教师板书:
证明:如图,在直线l 上任取一点C′(与点C不重合),
连接AC′,BC′,B′C′.
由轴对称的性质知,BC = B′C,BC′ = B′C′.
∴ AC+BC = AC+B′C = AB′,
AC′+BC′ = AC′+B′C′.
在△AB′C′中,AB′<AC′+B′C′,
∴ AC+BC<AC′+BC′.
即AC+BC最短.
总结:
最短路径问题
两点在直线同侧:两点连线与直线的交点.
两点在直线异侧:一点与另一点关于直线的对称点的连线与直线的交点.
原理:两点之间,线段最短.
设计意图:从异侧问题入手,由简到难,逐步深入,将同侧问题转化为异侧问题,渗透转化思想.
第三环节 【应用迁移 巩固提高】
例1.如图牧马人从A地出发,先到草地边某一处牧马,再到河边饮马,然后回到B处,请画出最短路径.
例2.架桥问题:如图,A、B两地在一条河的两岸,现要在河上造一座桥MN,桥造在何处可使从A到B的路径AMNB最短?(假定河的两岸是平行的直线,桥要与河垂直)
例3.如图,点P在∠AOB内部,问如何在射线OA、OB上分别找点C、D,使PC+CD+DP之和最小?
设计意图:对前面所学的解题方法与思路得以巩固,让学生形成技能,进一步体会感悟数学中的转化思想.
【答案】
例1.解:如图所示,分别作出点A关于MN的对称点A1,点B关于l对称点B1,
连接A1 B1,与MN和l分别交于点C,D,
则线路ACDB即为所求.
例2.解:如图所示,把河的两岸看成两条平行线a和b,
N为直线b上的一个动点,MN垂直于直线b,交直线a于点M.
问题转化为:当点N在b的什么位置时,AM+MN+NB最小,
因为河的宽度MN是固定的,问题转化为:
当点N在b的什么位置时,AM+NB最小.
将AM沿与河岸垂直的方向平移,
点M移动到点N,点A移动到点A',
则A'A = MN,
AM+NB = A'N+NB.
问题转化为:当点N在b的什么位置时,A'N+NB最小.
如图,在连接A',B两点的线中,线段A'B最短.
因此,线段A'B与直线b的交点N的位置即为所求.
即在点N处造桥MN,所得路径AMNB是最短的.
例3.解:如图,分别作点P关于OA,OB的对
称点P1,P2,
连接P1P2分别与OA,OB交于点C,D,
所得PC+CD+DP之和最小.
第四环节 【随堂练习 巩固新知】
1.如图,小明到小丽家有四条路,其中路程最短的是( )
① B.② C.③ D.④
2.如图,某村计划挖一条水渠将不远处的河水引到农田(记作点O),以便对农田进行灌溉,现设计了四条路线,其中最短的是( )
A.OA B.OB C.OC D.OD
3.如图,直线l是一条河,P,Q是两个村庄,欲在l上的某处修建一个水泵站,分别向P,Q两地供水,现有如下四种铺设方案,图中实线表示铺设的管道,则所需管道最短的是( )
如图,在四边形ABCD中,∠A = 90°,AD = 4,连接BD,BD⊥CD,∠ADB = ∠C,若P是BC边上一动点,则DP长的最小值为____.
如图,AD是等边△ABC的BC边上的高,AD = 6,M是AD上的动点,E是AC边的中点,则EM+CM的最小值为____.
设计意图:本环节主要考察学生对新学知识的理解及掌握情况.
【答案】
1.B 2.B 3.D 4.4 5.6
第五环节 【当堂检测 及时反馈】
1.(2020春 汉阳区期中)点P为直线l外一点,点A,B, C为直线l上三点,PA = 3 cm,PB = 4 cm,PC = 5 cm,则点P到直线l的距离( )
A.等于 4 cm B.等于 3 cm
C.小于 3 cm D.不大于 3 cm
2.(2019秋 浦北县期末)如图,等边△ABC的边长为 8,AD是BC边上的中线,E是AD边上的动点,F是AB边上一点,若BF = 4,当BE+EF取得最小值时,则∠EBC的度数为( )
A.15° B.25° C.30° D.45°
如图,四边形ABCD中,∠C = 50°,∠B = ∠D = 90°,E,F分别是BC,DC上的点,当△AEF的周长最小时,∠EAF的度数为( )
A.50° B.60° C.70° D.80°
4.(2019秋 武汉期中)如图,A、B是直线CD外两定点,P为直线CD上一动点,当PB-PA最大时,∠BPC = 40°.此时∠APC的度数为( )
A.40° B.80° C.100° D.140°
5.(2020春 和平区期末)如图,若∠MON = 42°,P为∠MON内一定点,OM上有一点A,ON上有一点B,当△PAB的周长取最小值时,则∠APB的度数为 .
6.(2020秋 双流区校级月考)如图,∠ABC = 30°,点D是∠ABC内的一点,且DB = 9,若点E,F分别是射线BA,BC上异于点B的动点,则△DEF的周长的最小值是 .
7.(2019秋 忻州期末)如图,在△ABC中,AB = AC,BC = 4,S△ABC = 12,点D,E分别是AB,BC的中点,点F在AC上,且FD⊥AB.若点P为线段DF上一动点,连接BP,EP,则△BPE周长的最小值是 .
8.(2019秋 梁子湖区期末)如图,∠AOB = 30°,M,N分别是OA,OB上的定点,P,Q分别是边OB,OA上的动点,如果记∠AMP = α,∠ONQ = β,当MP+PQ+QN最小时,则α与β的数量关系是 .
9.如图,要在街道l上修建一个奶吧D(街道用直线l表示).
(1)若奶吧D向小区A,B提供牛奶如图①,则奶吧D应建在什么地方,才能使它到小区A,B的距离之和最短?
(2)若奶吧D向小区A,C提供牛奶如图②,则奶吧D应建在什么地方,才能使它到小区A,C的距离之和最短?
10.如图,荆州护城河在CC'处直角转弯,河宽相等,从A处到达B处,需经两座桥(桥宽不计),设护城河以及两座桥都是东西、南北方向的,试问:桥架在何处,才能使从A到B的距离最短?
设计意图:通过小测反馈本节课学生对知识的掌握情况.
【答案】
D 2.C 3.D 4.A 5.96° 6.9
7.8 8.α-β = 90°
9.解:(1)连接AB与直线l交于点D,
奶吧D的位置如图①所示;
(2)作点A关于直线l的对称点A′,
连接A′C与直线l交于点D,
奶吧D的位置如图②所示.
10.解:作AF⊥河岸,且AF = 河宽,
作BG⊥河岸,且BG = 河宽,
连接GF,与河岸相交于E′、D′.
作DD′⊥河岸, EE′⊥河岸,
DD′、EE′即为桥的位置.
由两点之间线段最短可知,GF最小;
即当桥建于如图所示位置时,才能使从A到B的距离最短.
第六环节 【拓展延伸 能力提升】
1.如图,已知△ABC为等腰直角三角形,AC = BC = 4,∠BCD = 15°,P为CD上的动点,则|PA-PB|的最大值为 .
2.如图,AB⊥BC,AD⊥DC,∠BAD = 100°,在BC、CD上分别找一点M、N,当△AMN周长最小时,求∠MAN的度数是多少?
设计意图:通过有梯度的训练,提高学生对知识的综合运用能力.
【答案】
1.4
2.解:作A关于BC和CD的对称点A′,A″,连接A′A″,
交BC于M,交CD于N,则A′A″即为△AMN的周长最小值.
∵ ∠DAB = 100°,
∴ ∠AA′M+∠A″ = 180°-∠BAD = 180°-100°= 80°,
∵ ∠MA′A = ∠MAA′,∠NAD = ∠A″,
且∠MA′A+∠MAA′ = ∠AMN,∠NAD+∠A″ = ∠ANM,
∴ ∠AMN+∠ANM = ∠MA′A+∠MAA′+∠NAD+∠A″
= 2(∠AA′M+∠A″) = 2×80°= 160°,
∠MAN = 180°-160°= 20°.
故当△AMN周长最小时,∠MAN的度数是 20°.
第七环节 【总结反思 知识内化】
课堂小结:
这节课我们学到了什么?
两点在直线同侧:两点连线与直线的交点.
两点在直线异侧:一点与另一点关于直线的对称点的连线与直线的交点.
造桥选址:垂直河岸方向平移,使其他线段共线.
设计意图:使学生系统地了解本课核心知识,加深理解,建立内在联系.
第八环节 【布置作业 夯实基础】
